Глава 22. Магнитные взаимодействия. Магнитная индукция.Силы Лоренца и Ампера

Если заряд движется, то наряду с электрическим полем он создает еще одно поле — магнитное, которое действует на другие движущиеся заряды. В результате возникает дополнительное (наряду с кулоновским) взаимодействие движущихся электрических зарядов, которое называется магнитным. В результате магнитного взаимодействия возникает взаимодействие проводников с током.

В 1820 г. датский физик Х. Эрстед обнаружил, что проводник с током действует на магнитную стрелку. После этого стало ясно, что магнитное взаимодействие движущихся электрических зарядов и токов и взаимодействие постоянных магнитов имеют одну и ту же природу. На основании подробных исследований А. Ампер установил, что взаимодействие постоянных магнитов между собой и с токами можно объяснить, если предположить, что внутри магнитов есть электрические токи (в настоящее время известно, что эти токи имеют внутримолекулярную природу).

Для характеристики магнитного поля вводится векторная величина, которая называется индукцией магнитного поля и которая позволяет найти силы, действующие со стороны магнитного поля на движущиеся заряды.

Как правило, эту величину обозначают буквой . Для нахождения индукции в каждой точке магнитного поля, созданного проводником с током, используется закон Био-Савара-Лапласа и принцип суперпозиции. Закон Био-Савара-Лапласа позволяет найти поле , созданное бесконечно малым элементом проводника, а принцип суперпозиции требует сложить векторы индукции, созданные всеми элементами проводников. Закон Био-Савара-Лапласа в школьный курс физики, однако, не входит. В задачи ЕГЭ входят только вопросы, связанные с направлением вектора магнитной индукции (но не с величиной). Существует несколько вариантов правила нахождения направления вектора . Наиболее удобным является правило буравчика — оно более универсально, чем правило левой руки. Правило буравчика утверждает, что если вкручивать правыйбуравчик¹ по току в проводнике, то направление движения ручки в каждой точке пространства покажет направление вектора индукции магнитного поля в этой точке. Относительно величины достаточно помнить, что чем дальше от проводника, тем меньше индукция, и что внутри бесконечной катушки (бесконечного соленоида) магнитное поле направлено вдоль оси катушки и однородно.

Магнитное поле можно изобразить графически с помощью линий магнитной индукции. Линии магнитной индукции — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этой точке. Линии магнитной индукции проводят так, что их густота в каждой области пространства пропорциональна величине индукции в этой области. В отличие от силовых линий электрического поля линии магнитной индукции всегда являются замкнутыми.

На электрический заряд величиной , движущийся со скоростью в магнитном поле с индукцией , со стороны магнитного поля действует сила, которая называется силой Лоренца

(22.1)

где — угол между скоростью и вектором индукции. Направление силы Лоренца определяется следующим образом (см. рисунок).

1. Сила Лоренца перпендикулярна плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля (на рисунке эта плоскость показана тонким пунктиром).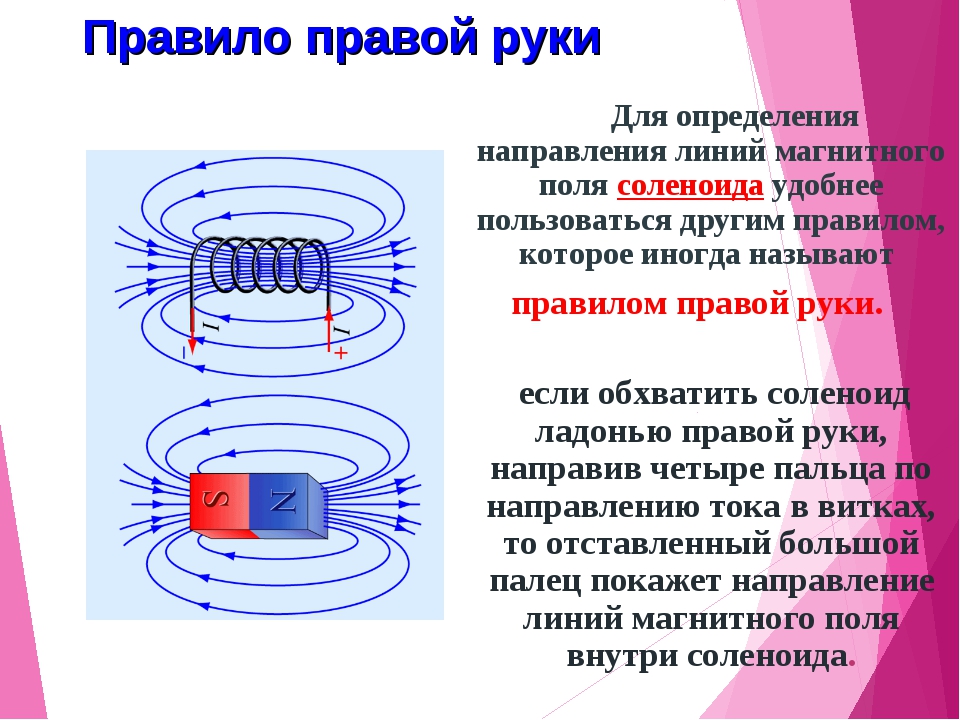

2. Выбор между двумя перпендикулярными направлениями осуществляется с помощью правила буравчика (или правила левой руки): если вращать правый буравчик так, что его ручка движется от вектора к вектору , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд (траектория ручки буравчика показана на рисунке изогнутой стрелкой).

3. Для отрицательного заряда направление силы Лоренца противоположно.

Можно также определять направление силы Лоренца по правилу левой руки: левую руку нужно расположить так, чтобы вектор входил в ладонь, направление четырех пальцев совпадало с направлением вектора скорости заряда, тогда направление отогнутого под прямым углом к четырем пальцам большого пальца покажет направление силы, действующей на положительный заряд (на отрицательный заряд действует сила противоположного направления).

Поскольку магнитное поле действует на движущиеся заряды, то магнитное поле действует и на проводник, по которому течет электрический ток. Если в магнитном поле с индукцией находится проводник длиной , по которому течет ток , то на этот проводник действует сила

(22.2)

где — угол между током и вектором индукции. Направлен вектор силы (22.2) перпендикулярно плоскости, в которой лежат вектор и проводник, причем в таком направлении, что если поставить правый буравчик перпендикулярно указанной плоскости и вращать его так, что ручка вращается от тока к вектору , то направление его вкручивания покажет направление силы (см. рисунок; плоскость в которой лежат проводник и вектор индукции обозначена тонким пунктиром, движение ручки буравчика — изогнутой стрелкой). Также для нахождения направления силы можно использовать правило левой руки. Сила (22.2), действующая со стороны магнитного поля на проводник с током, называется силой Ампера.

Рассмотрим теперь задачи.

Правильный ответ в задаче 22.1.1 — 4 (магнитное поле создается движущимися заряженными телами), в задаче 22.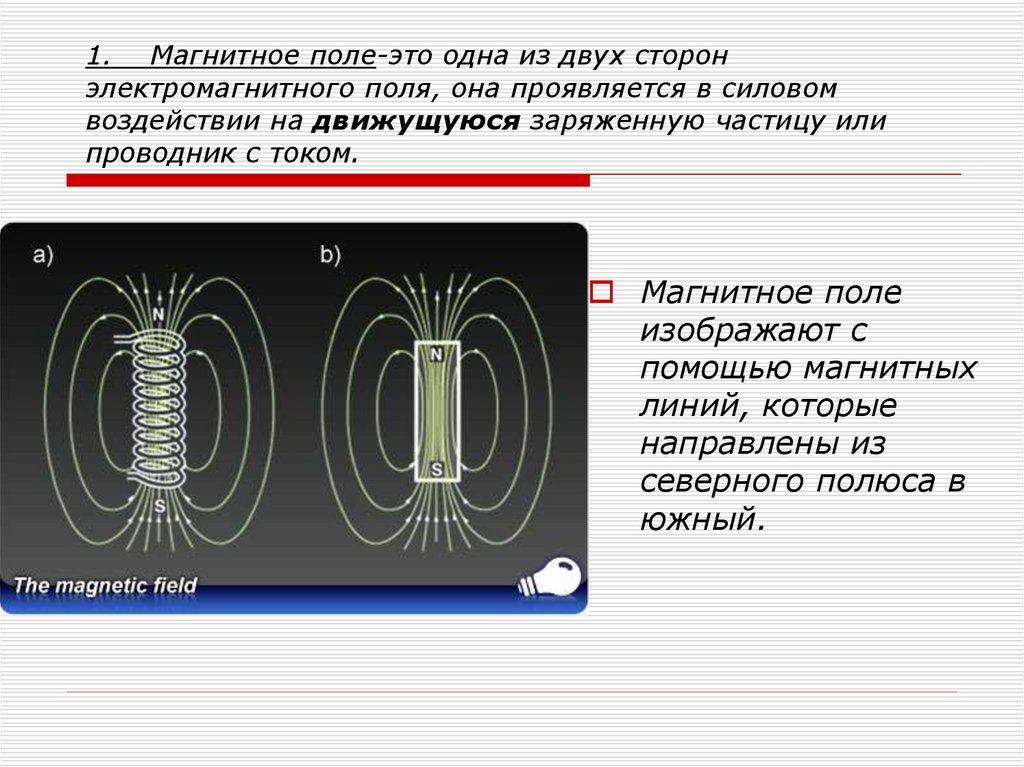 1.2 — 2 (в магнитном веществе есть незатухающие электрические токи). Что же касается того, заряжен магнит или нет, то от этого существование магнитного поля (если магнит покоится) не зависит.

В задаче 22.1.3 следует воспользоваться правилом буравчика. Если вкручивать буравчик по направлению тока в проводнике, то в точке его ручка будет двигаться за чертеж. Следовательно, за чертеж направлен в точке и вектор индукции магнитного поля (ответ 1).

Если вкручивать буравчик по току в кольце (в любой точке кольца), то ручка буравчика в центре кольца будет двигаться за чертеж. Поэтому правильный ответ в задаче 22.1.4 — 3.

Поскольку угол между скоростью заряда и вектором магнитной индукции равен нулю (задача 22.1.5), то согласно формуле (22.1) сила Лоренца, действующая на этот заряд, равна нулю (ответ 4).

Применим к проводнику с током из задачи 22.1.6 формулу (22.2) для силы Ампера. Имеем (ответ 2).

Как следует из формулы (22.

2) сила Ампера равна нулю, если угол между током и индукцией равен нулю или 180°. Из приведенных на рисунке в задаче 22.1.7 проводников, таковым является только проводник 1. Поэтому на него магнитное поле не действует (ответ 1).

Применяем к частице из задачи 22.1.8 (см. рисунок) правила нахождения направления силы Лоренца (пункты 1-3 после формулы (22.1)). Во-первых, сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля — т.е. либо за чертеж, либо на нас. Во-вторых, при вращении ручки буравчика, поставленного на чертеж в ту точку, где находится заряд, от вектора к вектору (в направлении меньшего угла между ними), буравчик будет «выкручиваться» из чертежа. А по-скольку частица заряжена положительно, сила Лоренца направлена «на нас» (ответ 1).

Используя правила для силы Ампера (формула (22.2) и текст после нее), найдем, что сила Ампера, действующая со стороны магнитного поля на проводник с током в задаче 22. 1.9, направлена «от нас» (ответ 3).

В задаче 22.1.10 следует сначала найти направление вектора магнитной индукции поля провода в той точке, где находится заряд, а затем использовать правила для силы Лоренца (формула (22.1) и текст за ней). Согласно результатам задачи 22.1.3, вектор в той точке, где находится заряд, направлен за чертеж (см. рисунок).

Вектор силы Лоренца направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. либо к проводу, либо от него. Ставим буравчик перпендикулярно этой плоскости и вращаем его так, что ручка движется от вектора к вектору (см. рисунок; буравчик нужно вращать по часовой стрелке, если смотреть снизу). При таком вращении буравчик будет вкручиваться вверх. А поскольку электрон заряжен отрицательно, то действующая на него сила направлена противоположно, т.е. от провода (ответ

2).

В задаче 22.2.1 используем принцип суперпозиции. Ток в горизонтальном кольце создает поле в его центре с индукцией, направленной вверх, ток в вертикальном кольце — с индукцией, направленной вправо (см.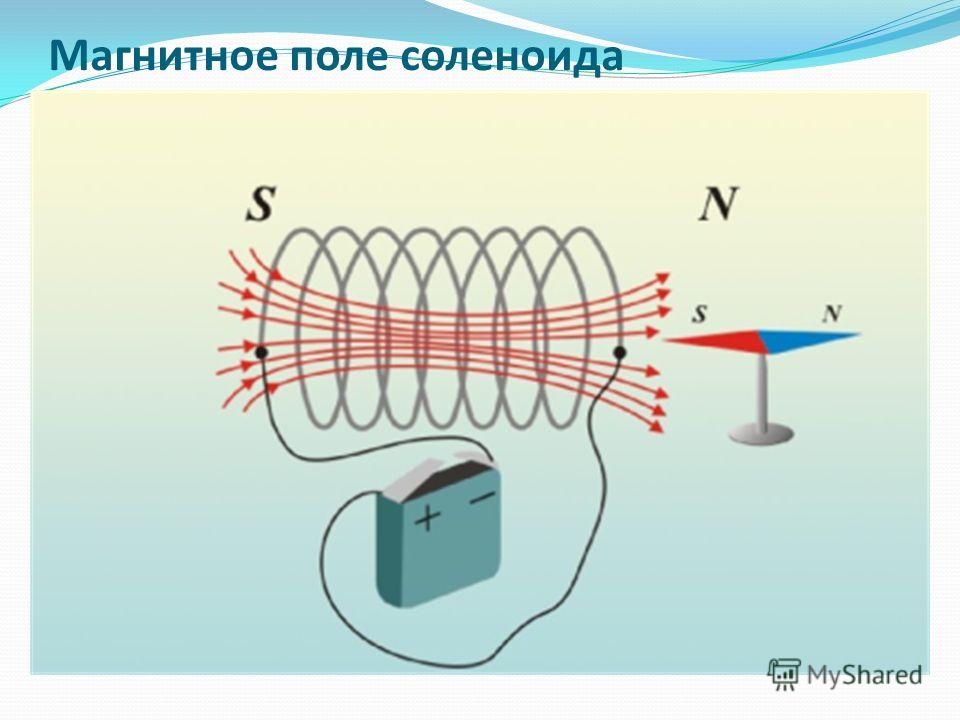 задачу 22.1.4.). Результат сложения этих векторов — индукция суммарного магнитного поля — направлена на «северо-восток» (ответ 1).

Ток в верхнем проводе (задача 22.2.2) создает поле с индукцией, направленной «за чертеж», ток в нижнем — «на нас». Результат их сложения зависит от величин этих векторов. Поскольку поле нижнего провода в точке больше поля верхнего (меньше расстояние), то вектор суммы направлен «на нас» (ответ 1).

Сила Лоренца в любой момент времени перпендикулярна скорости частицы. Поэтому угол между бесконечно малым перемещением частицы в любой момент времени и силой Лоренца, действующей на частицу в этот момент времени, — прямой. А поскольку в формулу для работы силы на бесконечно малом участке перемещения входит косинус угла между силой и перемещением, то работа силы Лоренца равна нулю (

задача 22.2.3 — ответ 3). Из этих рассуждений и теоремы об изменении кинетической энергии следует, что заряженная частица, движущаяся под действием магнитного поля, изменяет направление, но не величину своей скорости.

Если заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, то она движется по окружности, причем эта окружность лежит в плоскости, перпендикулярной линиям магнитной индукции. Радиус окружности можно найти из второго закона Ньютона для этой частицы

(22.3)

где и — масса частицы и ее заряд, — ускорение, — скорость, которая не изменяется по величине (см. предыдущую задачу), — индукция магнитного поля. В формуле (22.3) использовано известное выражение для центростремительного ускорения . Из формулы (22.3) получаем для радиуса окружности

(22.4)

Применяя формулу (22.4) к задаче 22.2.4 находим отношение радиусов окружности первой и второй частиц

(ответ 2).

Найдем сначала скорости протона и -частицы, ускоренных одним и тем же напряжением (задача 22.2.5). По теореме об изменении кинетической энергии имеем

где и — масса частицы и ее заряд, — скорость, которую частица приобретает после разгона (здесь предполагается, что начальная скорость частицы равна нулю). Из этой формулы находим отношение скоростей протона и -частицы , ускоренных одним и тем же напряжением

Поскольку заряд протона вдвое меньше заряда -частицы, а масса вчетверо меньше, то . Теперь из формулы (22.4) находим отношение радиусов окружности протона и  -частицы, ускоренных одним и тем же электрическим напряжением и движущихся в одном и том же магнитном поле

(ответ 4).

Период обращения заряженной частицы в магнитном поле (задача 22.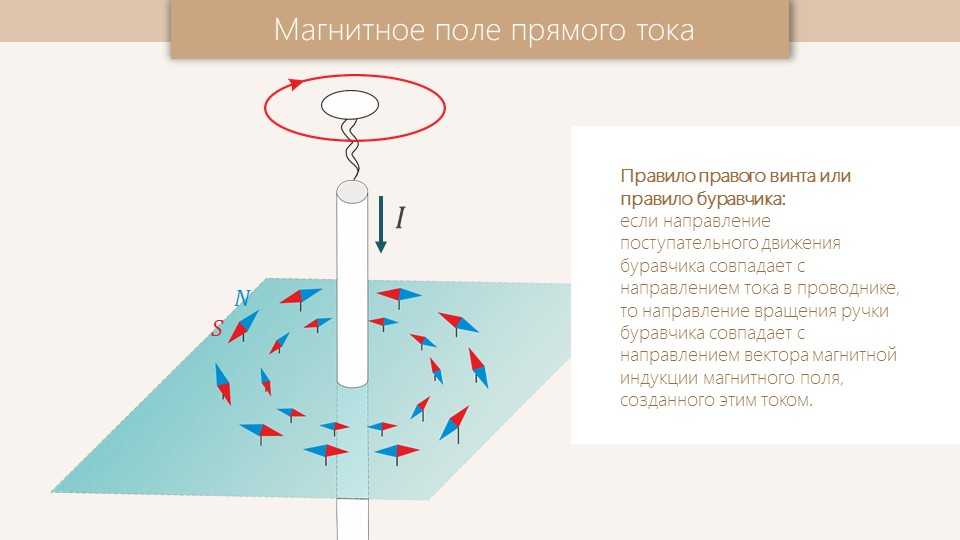 2.6) можно найти из следующих соображений. В однородном магнитном поле частица движется по окружности и за период проходит путь, равный длине этой окружности , где — ее радиус. Используя формулу (22.4) для радиуса траектории, получим для периода обращения

где — скорость частицы, — ее масса, — заряд, — индукция магнитного поля. Отсюда заключаем, что период обращения заряженной частицы в магнитном поле не зависит от ее скорости (ответ 3).

Индукция магнитного поля в задаче 22.2.7 должна быть направлена так, чтобы сила Лоренца, действующая на электрон, была направлена к центру окружности, по которой он движется (см. рисунок). А поскольку сила Лоренца перпендикулярна скорости и индукции, то вектор индукции может быть направлен в этой ситуации только «за чертеж» или «на нас». Воспользуемся далее правилом буравчика (см. текст после формулы (22.1)): если вращать буравчик так, что его ручка будет вращаться от скорости заряда к индукции магнитного поля , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд.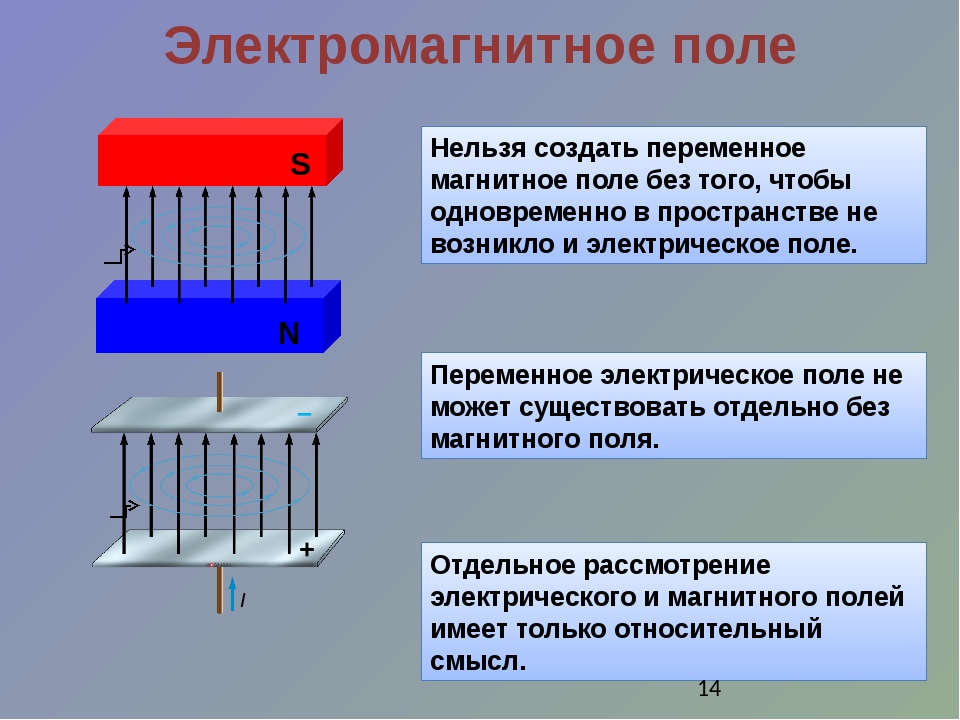 Для электрона ( < 0) направление силы противоположно. Непосредственной проверкой убеждаемся, что вектор индукции направлен «за чертеж» (ответ 4).

В области среднего провода (задача 22.2.8) ток в верхнем проводе создает магнитное поле с индукцией, направленной «от нас», ток в нижнем — «на нас» (см. задачу 22.1.3). Но ток в нижнем проводе вдвое меньше тока в верхнем, а индукция поля — пропорциональна току. Поэтому индукция суммарного поля верхнего и нижнего проводов в области среднего провода направлена «от нас». Согласно правилам нахождения направления силы Ампера (см. текст после формулы (22.2)) находим, что сила, действующая на средний провод со стороны магнитного поля верхнего и нижнего проводов, направлена вверх (ответ 1). Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.

В задаче 22.2.9 магнитное поле действует на рамку следующим образом.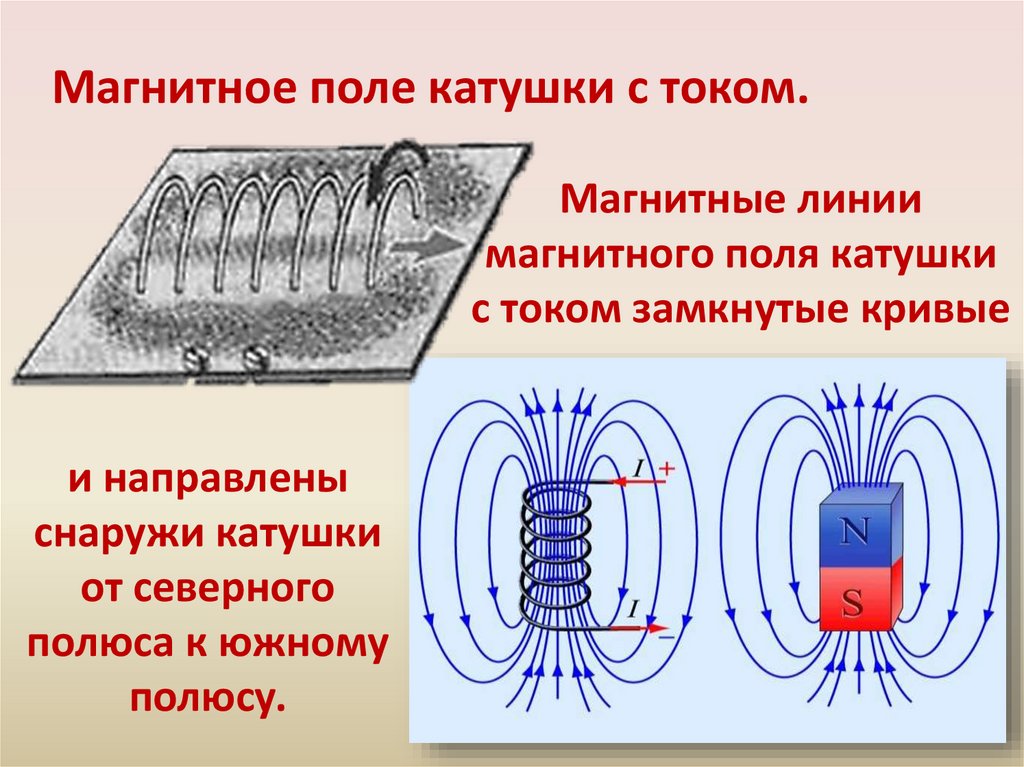 На стороны и , которые параллельны линиям индукции, поле не действует. На стороны и действуют силы Ампера, равные по величине , где — ток в рамке, — индукция магнитного поля, — длина стороны. Сила, действующая на сторону , направлена «на нас», на сторону — «от нас». Поскольку суммарная сила, действующая на рамку, равна нулю, как целое рамка перемещаться в пространстве не будет, а будет вращаться вокруг оси, показанной на рисунке пунктиром (ответ 4).

Задача 22.2.10 по формуле (22.2) находим силы Ампера, действующие на стороны треугольника

где — ток в контуре, и — длины сторон и , — индукция магнитного поля (последняя из приведенных формул следует из того, что сторона параллельна линиям индукции). Из теоремы синусов для треугольника

заключаем, что , а из правил для направления силы Ампера — что один из векторов или направлен «за чертеж», один — «на нас» (в зависимости от направления тока в контуре). Поэтому правильный ответ в задаче — 3.

Электромагнитное поле. Принцип действия электрогенератора

Урок № 47-169 Электромагнитное поле. Принцип действия электрогенератора.

Электромагнитное поле —особая форма материи, посред­ством которой осуществляется взаимодействие электрически заряженных тел.

В своей теории Максвелл показал следующее:

1. Электрическое поле может быть создано неподвижными зарядами.

2. Электрическое поле может быть создано переменным магнитным полем, и в этом случае его силовые линии являются замкнутыми; они охватывают изменяющийся магнитный поток (переменное электрическое поле- вихревое).

3. Магнитное поле не имеет источников, его силовые линии всегда замкнуты.

4. Переменное электрическое поле создает пе­ременное магнитное поле. Линии магнитной индукции этого поля охватывают линии на­пряженности электрического поля аналогично случаю соз­дания переменным магнитным полем вихревого электрического поля. Источник электромагнитно­го поля: ускоренно движущиеся заряды.

Возникновение магнитного поля при изменении электрического поля.

Максвелл допустил, что такого рода процесс реально происходит в при­роде. Во всех случаях, когда элек­трическое поле изменяется со вре­менем, оно порождает магнитное поле. Линии магнитной индукции этого поля охватывают линии напряженности электрического поля (см.рисунок), подобно тому, как линии напряженности электрического поля охватывают линии индукции пере­менного магнитного поля. Но теперь при возрастании напряженности электрического поля ( >о) на­правление вектора

индукции возникающего магнитного поля об­разует правый винт с направле­нием вектора Ё.При убывании напряженности электрического поля ( образует с направлением вектора Ё левый винт.

Согласно гипотезе Максвелла магнитное поле, например, при зарядке конденсатора после замы­кания ключа создается не только током в проводнике, но и изменя­ющимся электрическим полем, существующем в пространстве между обкладками конденсатора (см. рисунок). Причем изменяющееся электриче­ское поле создает такое же маг­нитное поле, как если бы между об­кладками существовал электриче­ский ток, такой же, как в провод­нике. Справедливость гипотезы Максвелла была доказана эксперимен­тальным обнаружением электромаг­нитных волн.

Электромагнитные вол­ны существуют только потому, что переменное магнитное поле

порож­дает переменное электрическое поле, которое в свою очередь порож­дает переменное магнитное поле

Электрические и магнитные по­ля — проявление единого целого — электромагнитного поля. Электро­магнитное поле — особая форма ма­терии, осуществляющая взаимодей­ствия между заряженными части­цами. Оно существует реально, т. е. независимо от нас, от наших знаний о нем. Но в зависимости от того, в какой системе отсчета рассматриваются электромагнитные процессы, проявляются те или иные стороны единого целого — электро­магнитного поля. Все инерциальные системы отсчета равноправны. Поэтому ни одному из обнаружи­ваемых проявлений электромагнит­ного поля не может быть отдано предпочтение.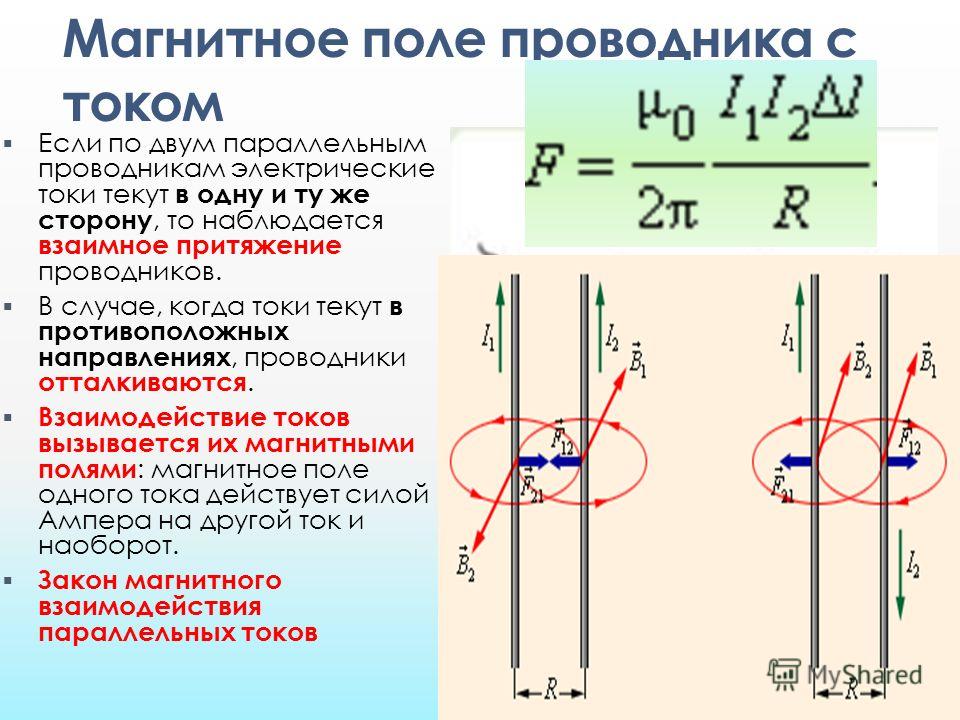

Работа электромагнитных сил. На прямолинейный провод длиной l с током I, расположенный в магнитном поле с индукцией В, направ­ленной перпендикулярно к l, действует электромагнитная сила F = = IlB (рис). Если этот провод переместится на расстояние b в направлении силы, то совершенная при этом работа А будет равна произведению силы тока на пересеченный магнитный поток:

А = Fb = IlBb = IBS = IФ.

Работа, совершаемая при перемещении контура с током в магнитном поле,

А = ± I (Ф₂ — Ф₁) = ± IΔФ, где ΔФ = Ф₂ — Ф₁ — разность потоков сквозь контур в конце и в начале движения, соответственно. Если контур движется под действием сил поля, то приращение ΔФ всегда положительно, т. е. силы поля стремятся увеличить поток через контур. Если же приращение отрицательно, то это может произойти только под действием внешних сил. По закону электромагнитной индукции Фарадея

электродвижущая сила индукции ε=-. Значение ЭДС, возникающей на концах проводника длиной l,движущегося в магнитном поле с индукцией В со скоростью v: ε=BIvsinα, где α — угол между направлениями векторов В и v . ЭДС индукции достигает наибольшей величины, когда v перпендикулярна к В.

Направление ЭДС индукции определяется в данном случае по правилу правой руки: если расположить правую руку так, чтобы вектор магнитной индукции В входил в ладонь, а отогну­тый большой палец направить вдоль вектора скорости, то четыре вытянутых пальца укажут направление ЭДС, а если концы провод­ника замкнуть,— то и тока.

Принцип действия электрогенератора. Генераторы тока

В генераторе переменного тока механическая энергия вращения преобразуется в электрическую энергию переменного тока. Состоит такой генератор из индуктора, т. е. электромагнита или магнита, создающего магнитное поле, и якоря — обмотки, в которой возникает переменная ЭДС.

Действие генератора переменного тока основано на явлении электромагнитной индукции. Чтобы понять, как он работает, рас­смотрим простейшую модель генератора, в которой индуктором яв­ляется постоянный магнит, а якорем — проволочная рамка (смотри рисунок).

Пусть магнит вращается вокруг рамки с постоянной частотой ν. Тогда за время t он совершит N=νt оборотов. Поскольку каждому обороту соответствует поворот на 360° или 2л радиан, то за все время движения магнит повернется на угол Δφ= 2πN= 2πνt=ωt, где ω=2πν — циклическая частота (или угловая скорость) вращения.

Находящаяся между полюсами маг­нита рамка в каждый момент време­ни будет пронизываться магнитным потоком, определяемым выражением Ф=ВScos

α= ВScos(φ₀+Δφ)= ВScos(ωt + φ₀), где φ = φ₀+Δφ — угол, под которым в

произвольный момент времени будет располагаться нормаль к рамке по от­ношению к силовым линиям магнит­ного поля (φ₀ — значение этого угла в начальный момент времени t=0).

Из-за непрерывного изменения угла φ пронизывающий рамку магнитный поток также будет меняться. Но при изменении магнитного потока возникает ЭДС индукции. Ве­личину этой ЭДС можно найти с помощью закона электромагнитной индукции в форме:=-Ф΄=-(ВScos φ)΄= ВSsin φ∙φ΄ где φ΄ — производная угла φ по времени t. Учитывая, что φ = ωt + φ₀, получаем: φ΄=(ωt + φ₀)΄= ω

Таким образом, ЭДС индукции в рамке оказывается равной:=ВS ω sin(ωt + φ₀) Если теперь подключить к выводам рамки нагрузку (устройство, потребляющее

электроэнергию), то через нее пойдет переменный ток.

Силу тока можно найти по закону Ома: I_i==sin(ωt + φ₀). Соответствующий график на рисунке.

Причиной появления тока в данном случае является действие на свободные электроны в проводнике вихревого электрического поля, порождаемого изменяющимся магнитным полем вращающегося маг­нита.

В рассмотренной модели генератора вращающейся частью (ро­тором) был магнит, а неподвижной частью (статором) служила рамка. Но переменный ток можно получить и при другой конструкции

генератора, когда ротором является рамка (якорь генератора), а статором — магнит. Причиной появления тока в этом случае будет уже не электромагнитная индукция, а действие на электроны, дви­жущиеся вместе с рамкой, магнитной силы Лоренца.

Особенностью такой конструкции генератора является наличие коллектора в виде скользящих контактов — колец и щеток, позволяющих избежать за­кручивания проводов, соединяющих вращающуюся рамку с нагрузкой (на рисунке). Аналогичным образом устроен и генератор постоянного тока.

Только вместо сплошных колец в нем используются полукольца (рис. 168, а). Благодаря такому «переключателю» контактов во внеш­ней цепи будет идти постоянный по направлению пульсирующий ток (рис. 169, а).

Пульсации этого тока можно уменьшить. В самом деле, учитывая, что наибольшие значения силы тока наблюдаются при прохождении рамкой положения, параллельного магнитным си­ловым линиям, вместо одной можно сделать две рамки во взаимно перпендикулярных плоскостях, а их концы вывести на противопо­ложные пластины четвертькольцевого коллектора (рис. 168, б). Через нуль тогда значения силы тока проходить уже не будут (рис. 169, б). Увеличивая число таких секций, можно добиться почти неизменного тока.

Задачи. Электромагнитное поле.

1. Определить энергию магнитного поля катушки, если индуктивность её 0,2 Гн, а сила тока в ней 0,4 А.

2. Сила тока в катушке 4 А. При какой индуктивности катушки энергия её магнитного поля будет равна 8 Дж.

3. Определить силу тока в катушке индуктивностью 0,8 Гн, если энергия магнитного поля равна 4 Дж.

4. Конденсатор ёмкостью С, заряженный до напряжения U,разряжается через катушку, индуктивность которой L,сопротивление равно нулю. Найти максимальный ток в катушке.

5. Определить энергию магнитного поля катушки, состоящей из 100 витков, если при силе тока 8 А в ней возникает магнитный поток 0,02 Вб.

6. По катушке протекает постоянный ток, создающий магнитное поле. Энергия этого поля равна 0,05 Дж, магнитный поток через катушку равен 0,01 Вб. Найти величину тока.

7. Цилиндрическая катушка длиной 50 см с площадью поперечного сечения 2 см² имеет индуктивность 0,2 мГн. При какой силе тока энергия единицы объёма магнитного поля внутри катушки ровна 1 м Дж/м³.

8. Чему равна объёмная плотность энергии магнитного поля в соленоиде без сердечника, имеющего плотную однослойную намотку проводом диаметром 0,2 мм, если сила тока в ней 0,1 А.

9. Найти энергию магнитного поля соленоида, в котором при силе тока 10 А возникает магнитный поток 0,5 Вб.

http://rusevents.pro/

3

Physics4Kids.com: Электричество и магнетизм: Магнитные поля

Магнитные поля отличаются от электрических полей. Хотя оба типа полей взаимосвязаны, они выполняют разные функции. Идея линий магнитного поля и магнитных полей была впервые рассмотрена Майклом Фарадеем , а затем Джеймсом Клерком Максвеллом .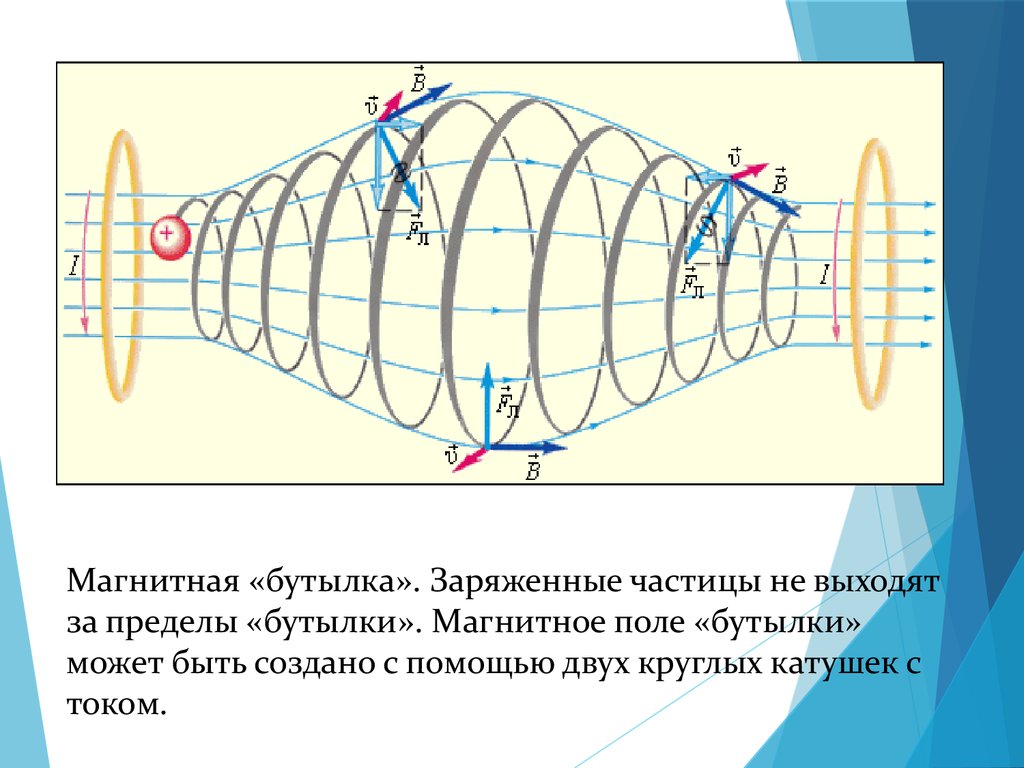 Оба этих английских ученых сделали великие открытия в области электромагнетизма .

Магнитные поля — это области, в которых объект проявляет магнитное влияние. Поля воздействуют на соседние объекты вдоль так называемых силовых линий магнитного поля. Магнитный объект может притягивать или отталкивать другой магнитный объект. Вы также должны помнить, что магнитные силы НЕ связаны с гравитацией. Величина гравитации зависит от массы объекта, а магнитная сила зависит от материала, из которого сделан объект.

Если вы поместите объект в магнитное поле, он будет затронут, и эффект будет происходить вдоль силовых линий. Во многих экспериментах в классе наблюдают, как маленькие кусочки железа (Fe) выстраиваются вокруг магнитов вдоль силовых линий. Магнитные полюса — это точки, в которых начинаются и заканчиваются силовые линии магнитного поля. Силовые линии сходятся или сходятся на полюсах. Вы, наверное, слышали о полюсах Земли. Эти полюса — места, где линии поля наших планет сходятся. Мы называем эти полюса северным и южным, потому что именно там они расположены на Земле. Все магнитные объекты имеют силовые линии и полюса. Он может быть маленьким, как атом, или большим, как звезда.

Вы знаете о заряженных частицах. Есть положительные и отрицательные заряды. Вы также знаете, что положительные заряды притягиваются к отрицательным зарядам. Французский ученый по имени Андре-Мари Ампер изучал взаимосвязь между электричеством и магнетизмом. Он обнаружил, что магнитные поля создаются движущимися зарядами (током). А на движущиеся заряды действуют магниты. С другой стороны, стационарные заряды не создают магнитных полей и не подвержены влиянию магнитов. Два провода с текущим током, расположенные рядом друг с другом, могут притягиваться или отталкиваться, как два магнита. Все дело в движущихся зарядах.

Магниты являются простыми примерами естественных магнитных полей. Но знаете что? Земля имеет огромное магнитное поле. Поскольку ядро ​​нашей планеты заполнено расплавленным железом (Fe), существует большое поле, которое защищает Землю от космической радиации и частиц, таких как солнечного ветра . Когда вы смотрите на крошечные магниты, они работают аналогичным образом. Вокруг магнита есть поле.

Как отмечалось ранее, ток в проводах создает магнитный эффект. Вы можете увеличить силу этого магнитного поля, увеличив ток через провод. Мы можем использовать этот принцип для создания искусственных регулируемых магнитов, называемых 9.0004 электромагниты , делая катушки из проволоки, а затем пропуская ток через катушки.

Или поищите на сайтах по конкретной теме.

• Обзор
• Сборы
• Проводники
• Электрические поля
• Магнитные поля
• Текущий
• Сопротивление
• Закон Фарадея
• Закон Кулона
• Магниты
• Питание постоянного тока
• Питание переменного тока
• Дополнительные темы

---

---

Солнечные частицы и магнитное поле Земли (видео НАСА)

Encyclopedia. com (Электромагнитное поле):
com (Магнитное поле):
http://www.encyclopedia.com/topic/Magnetic_Field.aspx
Википедия:
http://en.wikipedia.org/wiki/Magnetic_field
Британская энциклопедия:
http://www.britannica.com/EBcheckedfield/topic/3540980/magnetic_field

«Магнитная иллюзия» может создавать магнитные поля на расстоянии – Physics World

Магнитная иллюзия: длинный провод, окруженный магнитным репликатором, создает копию провода снаружи. (С разрешения: Phys. Rev. Lett. 10.1103/PhysRevLett.125.177204)

Физики из Великобритании и Испании заявляют, что нашли способ генерировать и управлять магнитными полями на расстоянии. Исследователи говорят, что это открывает возможность проецировать магнитные поля в недоступные места и позволяет дистанционно отключать магнитные источники. Одним из применений этой техники может быть улучшение контроля над магнитными микроботами и наночастицами в организме человека для медицинских приложений, таких как доставка лекарств и терапия магнитной гипертермией.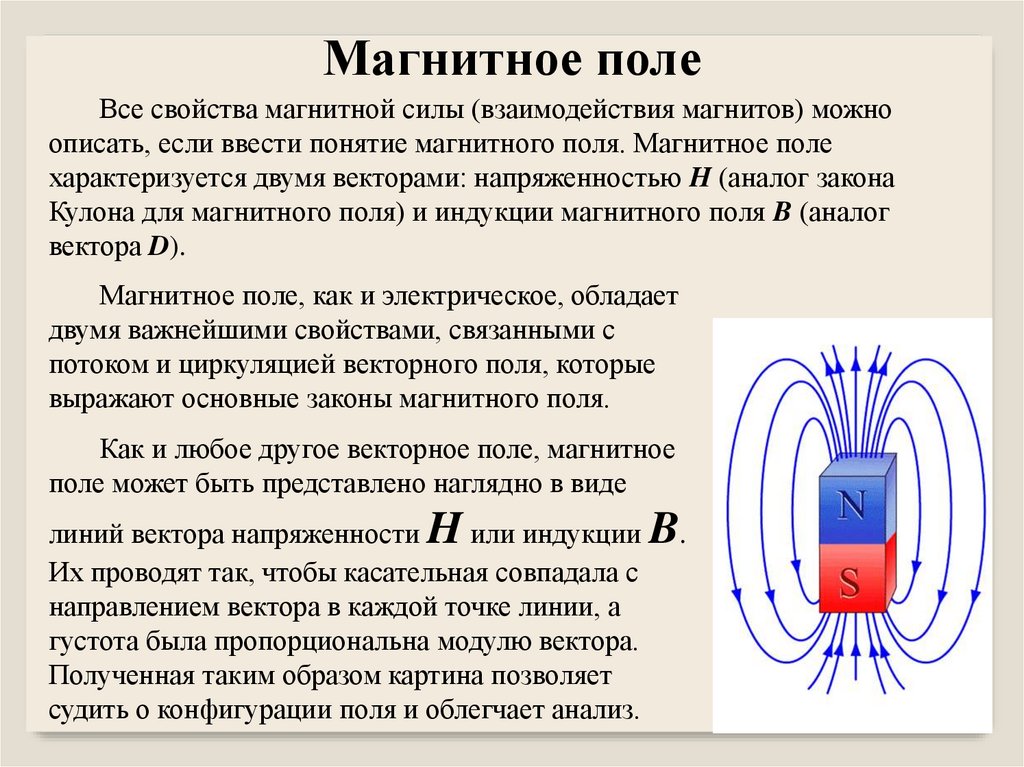

В последние годы метаматериалы позволили ученым манипулировать магнитными полями неожиданными способами, такими как создание магнитного плаща, который может сделать объект необнаружимым с точки зрения магнитного поля, и магнитных червоточин, которые переносят магнитное поле из одной точки пространства в другую.

В этой последней работе, опубликованной в Physical Review Letters , Роза Мах-Батлле из Автономного университета Барселоны и ее коллеги хотели проверить, могут ли они генерировать магнитное поле, которое появляется в свободном пространстве на расстоянии от его источника. .

Мах-Батль сообщает Миру Физики , что теория показала, что для достижения этого им потребуется магнитный материал с отрицательной магнитной проницаемостью. Магнитная проницаемость — это способность материала приобретать намагниченность в магнитных полях. Но не существует природных материалов с отрицательными значениями проницаемости.

Ранее исследователи показали, что метаматериал с отрицательной проницаемостью можно создать, применяя к материалу точное расположение токов.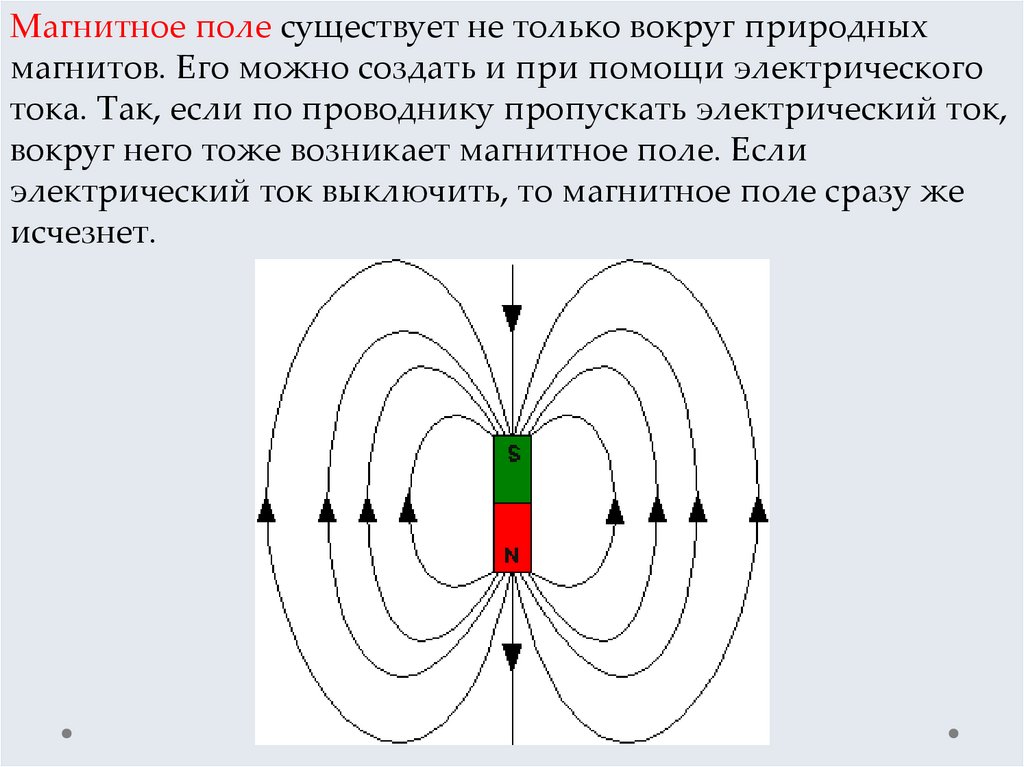 На этот раз их теория показала, что длинная цилиндрическая трубка с магнитной проницаемостью -1 будет действовать как линза для электромагнитных волн. Если бы этот цилиндр затем поместить вокруг магнитного источника, то распределение магнитного поля вне этой оболочки выглядело бы так, как будто оно было создано другим магнитным источником — своего рода магнитной иллюзией — на расстоянии от цилиндра.

Для создания метаматериала физики использовали цилиндр длиной 400 мм и радиусом 40 мм. При расположении 20 проводов контролировали поверхностные плотности тока на его внутренней и внешней поверхностях. Провод, проходящий через центр трубки, создавал магнитное поле.

Расчетное распределение магнитного поля, создаваемого 20 проводами с током, окружающими центральный провод (желтые точки), образующими репликатор. Магнитный источник, созданный на расстоянии, виден в заштрихованном прямоугольнике. (любезно предоставлено: Физ. Преподобный Летт. 10.1103/PhysRevLett.125.177204)

Исследователи показали, что с помощью этой установки они могут создавать магнитные источники на расстоянии от цилиндра.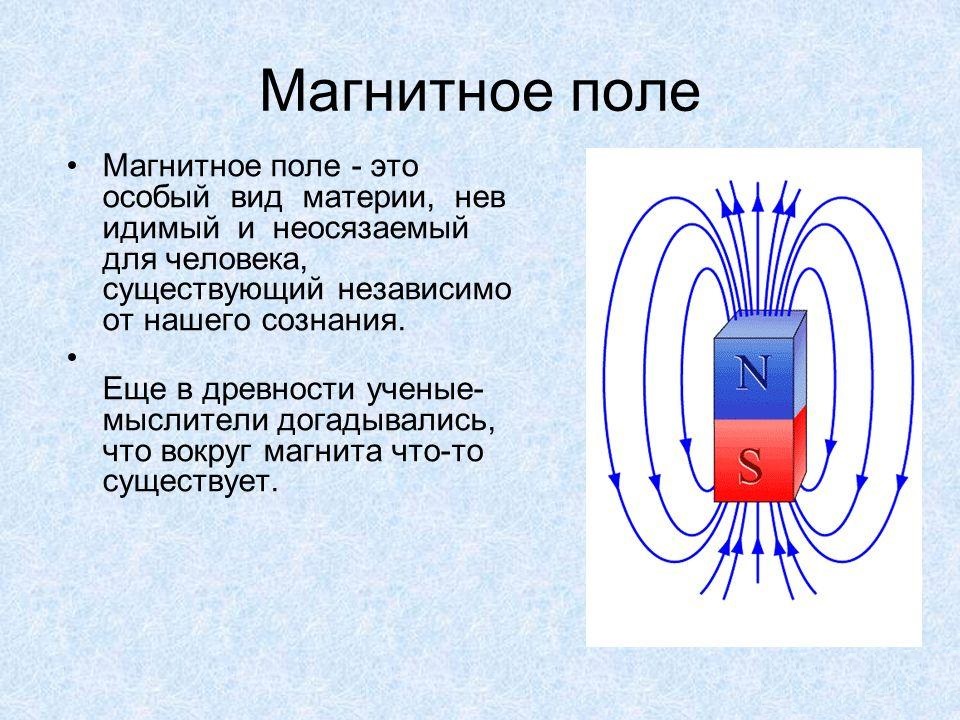 Они также продемонстрировали, что метаматериал можно использовать для удаленного подавления другого магнитного поля, установив провод с текущим по нему током в точке, где они ожидали появления проецируемого магнитного поля. Магнитные поля, создаваемые проводом и метаматериалом, компенсировали друг друга. Команда говорит, что этот метод можно использовать для удаленного подавления магнитных источников в недоступных местах, например, внутри стены или внутри человеческого тела.

Мах-Батль сообщает Миру Физики , что стоит отметить, что магнитное поле не аннулируется во всем пространстве. «Между нашим метаматериалом и источником есть цилиндрическая область, которую мы исключаем», — объясняет она. «В этой небольшой области поле не аннулируется, но в остальном пространстве мы бы аннулировали поле источника, который мы решили отменить».

Основное практическое применение этой техники, по мнению Мах-Батля, заключается не в устранении магнитных источников, а в возможности создавать иллюзию магнитного поля на расстоянии внутри недоступных пространств.