Интересные фигуры в геометрии: Картинки названия геометрических фигур для детей – Картинки названия геометрических фигур (30 фото) • Прикольные картинки и позитив | Дропшиппинг

Содержание

Картинки названия геометрических фигур для детей

Удивительный мир геометрических фигур! Давайте начнем изучать основы геометрии с этих чудесных картинок для детей с названиями. Уже в три года названия геометрических фигур постепенно вводят в активный словарь детей. Фигуры бывают разные: плоскостные и объемные. Фигуры простейшие изучают в математике в начальной школе: они могут состоять из отрезков и замкнутых линий. А планиметрию и стереометрию проходят в более старших классах. Желаем, чтобы знакомство с геометрическими фигурами приносило детям радость. Ну, что ж, приступим…

Картинки "Геометрические фигуры" с названиями (35 фото)

Этот удивительный мир геометрических фигур!

Плоскостные геометрические фигуры

Объемные геометрические фигуры

Из таких фигур можно строить замки!

Простейшие (основные) геометрические фигуры

Геометрические фигуры на плоскости

Какие геометрические фигуры изучают планиметрия и стереометрия

Виды фигур на плоскости

Криволинейные треугольники

Круг

Овал

Квадрат

Прямоугольник

Овал и эллипс похожи, но различия есть

Трапеция

Ромб

Четырехугольник

Параллелограмм

Правильные многоугольники

Треугольник

Различные виды треугольников

Куб

Шар

Цилиндр

Конус

Пирамида

Параллелепипед

Призма

Различные виды призм

Усеченный конус

Усеченная пирамида

Правильные многогранники

Октаэдр

Икосаэдр

Додекаэдр

Картинки названия геометрических фигур (30 фото) • Прикольные картинки и позитив

Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур.

Прямоугольник, ромб, круг.

Параллелепипед, шар, конус.

Круг, квадрат, овал.

Сложные геометрические фигуры с названием.

Ломанная, многоугольник, отрезок.

Конус, цилиндр, сфера.

Картинка про название геометрических фигур.

Полукруг, треугольник, трапеция.

Квадраты, круги, овалы.

Разные фигуры из геометрии.

Параллелограмм, восьмиугольник.

Квадрат, шестиугольник, семиугольник.

Звезда, призма, сфера.

Предметная картинка про геометрические фигуры.

Большой красный конус.

Оранжевый ромб.

Синий куб.

Название геометрических фигур

Геометрические тела.

Разные пирамиды.

Простая картинка названия геометрических фигур.

Фиолетовый ромб.

Красивый конус.

Овал, трапеция, ромб.

Много фигур из учебника геометрии.

Куб, сфера.

Сердце, звезда, овал.

Геометрические фигуры и их названия.

Список правильных многомерных многогранников и соединений — Википедия

Материал из Википедии — свободной энциклопедии

Примеры правильных многогранников
Правильные (2D) многоугольники
Выпуклые	Звёздчатые
{5}	{5/2}
Правильные 3D-многогранники
Выпуклые	Звёздчатые
{5,3}	{5/2,5}
Правильные 2D-замощения
Евклидовы	Гиперболические
{4,4}	{5,4}^[en]
Правильные 4D-многогранники
Выпуклые	Звёздчатые
{5,3,3}	{5/2,5,3}^[en]
Правильные 3D-замощения
Евклидовы	Гиперболические
{4,3,4}	{5,3,4}

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику (n-1)-сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера, которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера

[en]. Другой связанный символ — диаграмма Коксетера — Дынкина, которая представляет группу симметрии (без помеченных кружком узлов) и правильные многогранники или замощения с обведённым кружком первым узлом. Например, куб имеет символ Шлефли {4,3}, с его октаэдральной симметрией^[en] [4,3] или

, представляется диаграммой Коксетера

Правильные многогранники сгруппированы по размерности, а затем по форме — выпуклые, невыпуклые и бесконечные. Невыпуклые виды используют те же вершины, что и выпуклые, но имеют пересекающиеся фасеты (грани максимальной размерности = размерности пространства – 1). Бесконечные виды замощают евклидово пространство на единицу меньшей размерности.

Бесконечные формы можно расширить до замощения гиперболического пространства. Гиперболическое пространство подобно обычному пространству, но параллельные прямые с расстоянием расходятся. Это позволяет вершинным фигурам иметь отрицательные угловые дефекты. Например, в вершине может сходиться семь правильных треугольников, лежащих на плоскости. Это нельзя осуществить на обычной (евклидовой) плоскости, но можно сделать при некотором масштабе на гиперболической плоскости.

Многогранники, удовлетворяющие более общему определению и не имеющие простых символов Шлефли, включают правильные косые многогранники и бесконечноугольные правильные косые многогранники с неплоскими фасетами или вершинными фигурами.

Таблица показывает сводку правильных многогранников по размерностям.

	Конечные			Евклидовы	Гиперболические			Соединения
Разм.	Выпук- лые	Звёзд- чатые	Косые	Выпук- лые	Компак- тные	Звёзд- чатые	Параком- пактные	Выпук- лые	Звёзд- чатые
1	1	0	0	1	0	0	0	0	0
2	∞	∞	∞	1	1	0	0	∞	∞
3	5	4	?	3	∞	∞	∞	5	0
4	6	10	?	1	4	0	11	26	20
5	3	0	?	3	5	4	2	0	0
6	3	0	?	1	0	0	5	0	0
7	3	0	?	1	0	0	0	3	0
8	3	0	?	1	0	0	0	6	0
9+	3	0	?	1	0	0	0	*	0

* 1, если размерность имеет вид 2^k − 1, 2, если размерность является степенью двойки, 0 в противном случае.

Не существует правильных звёздчатых замощений в евклидовом пространстве любой размерности.

Диаграмма Коксетера — Дынкина представляет зеркальные «плоскости» как узлы, и помещает кружок вокруг узла, если точка не лежит на плоскости. Отрезок, { },

— это точка p и зеркальный образ точки p, а также отрезок между ними.

Одномерный многогранник (1-многогранник) — это замкнутый отрезок, ограниченный двумя конечными точками. 1-многогранник является правильным по определению и представляется символом Шлефли { }^[1]^[2] или диаграммой Коксетера с единственным помеченным кружком узлом, . Норман Джонсон^[en] дал им название дайтел и символ Шлефли { } ^[3].

Будучи тривиальным в качестве многогранника, дайтел возникает в качестве рёбер многоугольников и многогранников^[4]. Он используется в определении однородных призм (как в символе Шлефли { }×{p}) или в диаграмме Коксетера как прямое произведение отрезка и правильного многоугольника ^[5].

Двумерное пространство (многоугольники)[править | править код]

Двумерные многогранники называются многоугольниками. Правильные многоугольники имеют равные стороны и вписаны в окружность. Правильный p-угольник представляется символом Шлефли {p}.

Обычно только выпуклые многоугольники считаются правильными, но звёздчатые многоугольники наподобие пентаграммы можно также считать правильными. Они используют те же вершины, что и выпуклые формы, но соединение происходит другим путём, при котором окружность обходится более одного раза.

Звёздчатые многоугольники следует называть скорее невыпуклыми, чем вогнутыми, поскольку пересечение рёбер не образует новых вершин и все вершины находятся на окружности.

Выпуклые[править | править код]

Символ Шлефли {p} представляет правильный p-угольник.

Название	Треугольник (2-симплекс)	Квадрат (2-ортоплекс) (2-куб)	Пятиугольник	Шестиугольник	Семиугольник	Восьмиугольник
Шлефли	{3}	{4}	{5}	{6}	{7}	{8}
Симметрия	D₃, [3]	D₄, [4]	D₅, [5]	D₆, [6]	D₇, [7]	D₈, [8]
Коксетер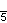
Рисунок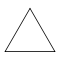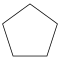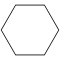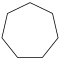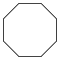
Название	Девятиугольник	Десятиугольник	Одиннадцатиугольник	Двенадцатиугольник	Тринадцатиугольник	Четырнадцатиугольник
Шлефли	{9}	{10}	{11}	{12}	{13}	{14}
Симметрия	D₉, [9]	D₁₀, [10]	D₁₁, [11]	D₁₂, [12]	D₁₃, [13]	D₁₄, [14]
Дынкин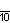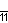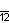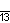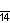
Рисунок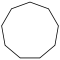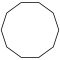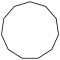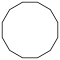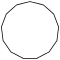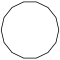
Название	Пятнадцатиугольник	Шестнадцатиугольник	Семнадцатиугольник	Восемнадцатиугольник	Девятнадцатиугольник	Двадцатиугольник	…p-угольник
Шлефли	{15}	{16}	{17}	{18}	{19}	{20}	{p}
Симметрия	D₁₅, [15]	D₁₆, [16]	D₁₇, [17]	D₁₈, [18]	D₁₉, [19]	D₂₀, [20]	D_p, [p]
Дынкин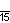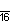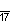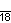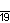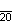
Рисунок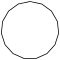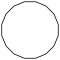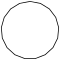

Для чего нужны геометрические фигуры. Часть 1

Пользу раннего развития сложно оспорить. Активное обучение способствует формированию креативной и гармоничной личности. С ранних лет малыш привыкает узнавать все новое, и в дальнейшем не будет проблем с усвоением информации.

1) изучение форм предметов помогает ребенку расширить кругозор, словарный запас и развивает наблюдательность

2) получение новых знаний – всегда тренировка для мозга

3) развитие логического мышления

4) развитие пространственного представления

5) совершенствование математических и аналитических способностей

6) развитие творческих способностей

7) тренировка ассоциативного мышления (малыш учится проводить аналогию)

С чего начать изучение?

Начать стоит с самых простых азов. В первую очередь познакомить малыша с кругом, треугольником и квадратом.

Самый простой и доступный способ – это показывать формы на примере бытовых предметов. Например: тарелка круглая, окно квадратное и т.д. Со временем затрагивайте не только мебель в доме, но и предметы на улице и детской площадке.

Для деток до 1,5 лет разговоры с мамой – отличный источник изучения окружающего мира. Даже если вам кажется, что малыш не обращает на это внимания, не прекращайте повторять. Любая информация при повторении обязательно запомнится малышу.

При правильном подходе, в 2 года детки смогут отличать:

-круг

-квадрат

-треугольник

И могут найти нужную фигуру среди других геометрических фигур.

К 3 годам можно добавить:

-овал

-ромб

-прямоугольник

В 4 года и старше – могут анализировать сложные картинки, состоящие из множества фигур

Игры с геометрическими фигурами.

1) В сумочку или непрозрачный пакет прячем фигуры. Ребенок берет в руки предмет и пытается определить его форму не глядя.

2) Попросите ребенка назвать формы, которые могут кататься, фигуры с углами и без.

3) Ассоциации. Пусть малыш расскажет, на что похож треугольник, круг, овал и другие фигуры.

Во время создания картин проговаривайте фигуры предметов. Например: «мы сделаем квадратный дом с треугольной крышей».

Изучаем фигуры с ребенком 2-3 года.

В этом возрасте дети уже знают цвета и ориентируются в размерах, поэтому для изучения фигур подходят следующие занятия:

1) Найди лишнее. Можно взять несколько квадратов и один треугольник. Малыш должен выбрать какой предмет отличается от других. Для усложнения можно узнать, почему он выбрал именно эту фигуру.

2) Разложи правильно. Можно взять 4 фигуры (например: 2 круга и 2 квадрата) и предложить ребенку разложить их в две стопки. Можно усложнить задание: взять 9 фигур и разложить на 3 стопки.

3) Сортировка. Используем фигуры разных размеров и цветов. Например: синие треугольники – в одну сторону, красные квадраты – в другую. Это занятие укрепит знание цветов и позволит лучше ориентироваться в размерах.

4) Найди сокровище. Понадобится миска с любой крупой, в которой спрячьте различные фигурки. Когда малыш их будет находить, обязательно должен дать название найденному предмету. Такая игра не оставит равнодушным ни одного ребенка!

Необычные геометрические фигуры

Ульянов А.Е. 1

1МАОУ «СОШ №12»

Мурзина Т.А. 1

1МАОУ «СОШ №12»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

С самого первого класса на уроках математики мы стали знакомиться с различными геометрическими фигурами. Меня это очень заинтересовало. Рассматривая предметы я заметил, что многие из них не похожи на фигуры, изучаемые в школе.

Это мне показалось очень интересным, и я решил исследовать тему: «Необычные геометрические фигуры». В данной работе, я решил заняться изучением и исследованием геометрических фигур, в частности листа Мебиуса.

В данной работе расскажу о тех геометрических фигурах, которые мы не изучаем на уроках геометрии в школе, но именно они окружают нас в действительности, в архитектуре, в компьютерных играх и головоломках.

Цель данной работы: выявить необычные геометрические фигуры, используемые в современной миреи выяснить их происхождение и применение.

Задачи работы:

Выделить необычные геометрические фигуры.

Проанализировать основные особенности использования необычных геометрических фигур в окружающем нас мире

Методы исследования:

— изучение литературы по данному вопросу

— наблюдение в повседневной жизни.

Гипотеза: в процессе работы над проектом я хочу уточнить, нужны ли знания о необычных геометрических фигурах в повседневной жизни.

Основная часть

1.Теоритическая часть

Мы привыкли к традиционным формам евклидовой геометрии, знакомой нам уже 23 века: линии, прямоугольники, окружности, многоугольники на плоскости и т.д. И хотя это единственный вид геометрии, с которым знакомы многие люди, евклидова геометрия – всего лишь один из примеров существующих геометрий. Природа обычно не выражает себя в симметричной или правильной форме, а евклидова геометрия не располагает необходимыми инструментами, чтобы изучать ее феномены. Например, облако может походить на сферу, но не является ею, некоторые горы и холмы напоминают конусы, но это не так, а реки и беговые линии далеки от прямых линий. Тем не менее в творениях природы скрыт незримый порядок, и тех, кто решится присмотреться к ним повнимательнее, ждут сюрпризы.[5]

1.1 Лист Мёбиуса

Лента Мебиуса является одной из самых необыкновенных геометрических фигур. Несмотря на ее необычность, ее легко сделать в домашних условиях.

Лента Мебиуса – это трехмерная неориентируемая фигура с одной границей и стороной. Этим она уникальна и отлична от всех других предметов, которые могут встретиться в повседневной жизни. Ленту Мебиуса также называют листом Мебиуса и поверхностью Мебиуса. Она относится к топологическим объектам, то есть объектам непрерывным. Такие объекты изучает топология — наука, исследующая непрерывность среды и пространства.

Интерес вызывает уже само открытие ленты. Два математика, несвязанных между собой, открыли ее в одном и том же 1858 году. Этими открывателями были Август Фердинанд Мебиус и Иоганн Бенедикт Листинг.

Условно различают ленты по способу сворачивания: по часовой стрелке и против часовой стрелки. Их еще называют правая и левая. Но различить «на глаз» вид ленты невозможно.

Сделать такую фигуру чрезвычайно просто: нужно взять ленту ABCD. Свернуть ее так, чтобы соединить точки A и D, В и С, склеить соединенные концы.

Лента Мебиуса имеет характерные свойства, они не меняются, если ленту сжимать, комкать или резать вдоль.

К этим свойствам относятся:

Односторонность. Если взять ленту Мебиуса и начать закрашивать в любом ее месте и направлении, то постепенно вся фигура будет закрашена целиком, при этом фигуру не нужно будет переворачивать.

Непрерывность. Каждую точку этой фигуры можно соединить с другой ее точкой, при этом ни разу не выходя за края ленты.

Двусвязность (или двумерность). Лента остается цельной, если резать ее вдоль. Из нее не получатся в этом случае две разные фигуры.

Отсутствие ориентированности. Если представить, что человек мог бы идти по этой фигуре, то при возвращении в точку начала путешествия, он бы превращался в свое отражение.[8]

Лист Мебиуса – неиссякаемый источник для творчества писателей, художников и скульпторов. Его упоминание часто встречается в фантастической и мистической литературе. На его свойствах основывались художественные вымыслы о возникновении Вселенной, устроенности загробной жизни, передвижении во времени и пространстве. Лист Мебиуса упоминали в своих произведениях Артур Кларк, Владислав Крапивин, Хулио Кортасар, Харуки Мураками и многие другие.

Известным художником Эшером был создан ряд литографий с использованием ленты. На наиболее известной его работе муравьи ползут по листу Мебиуса.

Часто используют эту геометрическую фигуру ювелиры при создании дизайна драгоценностей.

Ленту Мебиуса широко применяют в науке и промышленности. Она является источником для множества научных исследований и гипотез. Существует, например, теория, что ДНК – это часть листа Мебиуса. Исследователи в области генетики уже научились разрезать одноцепочную ДНК так, чтобы получить из нее ленту Мебиуса. Физики говорят о том, что оптические законы базируются на свойствах листа Мебиуса. Например, отражение в зеркале – это своего рода передвижение во времени по аналогичной траектории. Есть научная гипотеза о том, что Вселенная – это гигантская лента Мебиуса.

В начале 20 века Никола Тесла изобрел резистор Мебиуса, который противостоит потоку электроэнергии, не вызывая при этом электромагнитных помех. Он состоит из двух проводящих поверхностей, которые скручены на 180 ° и образуют ленту Мебиуса.

Полоса ленточного конвейера (транспортирующей машины непрерывного действия) сделана в форме ленты Мебиуса. Такая поверхность позволяет увеличить срок использования ленты, так как ее изнашивание будет происходить равномерно. Используют форму ленты Мебиуса и при записи на непрерывную пленку.

Лист Мебиуса применялся в матричных принтерах для продления срока годности красящей ленты.

На основе ленты Мебиуса создано абразивное кольцо в механизмах для заточки, работает автоматическая передача.

В настоящее время многие изобретатели пользуются свойствами данной ленты для проведения экспериментов и создания новых устройств.

Лента Мебиуса продолжает вызывать стойкий интерес, не только у математиков и изобретателей, но и у обычных людей. Она вдохновляет деятелей искусства на создание загадочных произведений и фантастических теорий. Эксперименты с этой интересной фигурой – увлекательное занятие, как для взрослого, так и для ребенка. Ее свойства нашли свое применение в науке, технике и в быту. Лента Мебиуса — это занимательная математическая загадка, скрывающая в себе смысл идеалистического понимания устройства Вселенной, ее воздействие на нашу жизнь можно изучать бесконечно.[6]

1.2Треугольник Рёло

Треуго́льникРёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Его можно построитьс помощью одного циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выберется произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей. Треугольник Рёло является плоской геометрической фигурой.

Треугольник Рёло назван по имени Франца Рёло – немецкого учёного-инженера, подробно исследовавшего его. Кроме того, Франц Рело использовал его в своих механизмах. Рёло не является первооткрывателем этой фигуры, хотя он и подробно изучил её. В частности, он рассматривал вопрос о том, сколько контактов необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась. Некоторые математики считают, что первым продемонстрировал идею треугольника из равныхдугокружностиЛеонард Эйлер в XVIII веке. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло. В XIII веке, создатели церкви Богоматери в Брюгге использовали треугольник Рёло в качестве формы для некоторых окон. Следует отметить, что треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат, а также в правильный шестиугольник.

Треугольник получил распространение в технике — на его основе были созданы кулачковые игрейферные механизмы, роторно-поршневой двигатель Ванкеля и даже дрели, позволяющие сверлить квадратные отверстия. Так, в 1914 году английский инженер Гарри Джеймс Уаттс изобрёл инструмент для сверления квадратных отверстий,с 1916 года сверла находятся в серийном производстве. Сверло Уаттса представляет собой треугольник Рело, в котором заточены кромки и прорезаны углубления для отвода стружки.

В форме треугольника Рёло можно изготавливать крышки для люков — опытным путем доказано, что благодаря постоянной ширине они не могут провалиться в люк. В Сан-Франциско, для системы рекуперированияводыкорпуса люков имеют форму треугольника Рёло. За счет того, что у треугольника Рёло площадь меньше, чем у круга, себестоимость люков в форме треугольников Рёло была бы ниже, чем у традиционно круглых. Перейдя на серийное производство люков в форме треугольника Рёло, на мой взгляд, можно было бы быстрее решить проблему открытых колодцев и избежать травматизма и смертей людей.[4]

1.3 Тессеракт

Тессеракт — четырёхмерный гиперкуб — аналог куба в четырёхмерном пространстве.

Согласно Оксфордскому словарю, слово «tesseract» было придумано и начало использоваться в1888 году Чарльзом ГовардомХинтоном (1853—1907) в его книге «Новая эра мысли». Позже некоторые люди назвали ту же самую фигуру тетракубом— четырёхмерным кубом.

Тессеракт в искусстве

В серии фильмов Кинематографическая вселенная Marvel тессеракт – это ключевой элемент сюжета, космический артефакт в форме гиперкуба.

Сюжет фильма «Мстители» сосредоточен на использовании куба «Тессеракт» как неиссякаемого источника космической энергии, для открытия портала в другое «измерение» с целью осуществления плана по захвату мира.

Телесериал «Андромеда» использует тессеракт-генераторы как устройство заговора. Они прежде всего предназначены для того, чтобы управлять пространством и временем.

Роберт Э. Хайнлайн упоминал гиперкубы в трех научно-фантастических рассказах. В «Доме четырех измерений» он описал дом, построенный как развертка тессеракта, а затем вследствие землетрясения «сложившийся» в четвертом измерении и ставший реальным тессерактом. [5]

Кресты на некоторых христианских храмах и монастырях Египта напоминают развертку тессеракта.

Картина «Распятие на кресте» (Corpus Hypercubus) Сальвадора Дали.[3]

1.4Фрактал

Фракта́л (лат. «fractus» — дроблёный, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает следующим свойством: фигура является самоподобной или приближённо самоподобной.

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы». Природные объекты часто имеют фрактальную форму.[3]

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных и т. д. Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера. Так, например, в физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, кактурбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Одни из наиболее мощных приложений фракталов лежат в компьютерной графике. Во-первых, это фрактальное сжатие изображений, и во-вторых, построение ландшафтов, деревьев, растений и генерирование фрактальных текстур. Достоинства алгоритмов фрактального сжатия изображений — очень маленький размер упакованного файла и малое время восстановления картинки. Оно основано на идее о том, что вместо самого изображения можно хранить сжимающее отображение. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили. Склонность фракталов походить на горы, цветы и деревья эксплуатируется некоторыми графическими редакторами,например фрактальные облака из 3D studio MAX, фрактальные горы в WorldBuilder.

Архитектура, начиная с фрагментов, деталей и заканчивая пространством города в целом – это система, обладающая фрактальными свойствами, которые нельзя не учитывать при формировании городской среды и проектировании новых объектов внутри неё. Город по своей сути – уникальное явление соединения творческих и технических усилий человека, социальных взаимодействий и воздействий природных процессов. Представление города как особой архитектурной системы – естественно сложившейся фрактальной структуры, развивающейся по не всегда понятным на первый взгляд алгоритмам, вполне оправдано. Фрактальными свойствами обладают не только здания, сооружения, кварталы, улицы, районы, но вся городская среда в целом, рассматриваемая как непрерывная структура в пространстве и во времени, развивающаяся функционально во взаимосвязи с изменяющейся пространственной организацией города.

Принципы фракталоподобного формообразования в архитектуре применяются с давних времен, и хотя использование фрактальных правил построения в архитектуре далеко не всегда оказывалось математически выверенным, но в поиске и создании художественно выразительных пропорций архитекторов вели их интуиция и талант, чувство гармонии и высокий профессионализм.[4]

Практическая часть

Путешествие по листу Мёбиуса

Путешествие по листу бесконечности могло бы продолжаться вечно.

Если взять ножницы и немножко поколдовать над этой загадочной поверхностью, то получится создать дополнительные необычные фигуры. Если резать ее вдоль, по линии, удаленной от краев на равное расстояние, то получится закрученная «Афганская лента».[9]

Если полученную ленту разделить вдоль, посередине, то образуются две ленты, взаимопроникающие друг в друга.

Если разрезать ленту Мебиуса с тремя или большим количествам полуоборотов, то получатся кольца, называющиеся парадромными.[8]

Если склеить вместе две ленты Мебиуса вдоль границ, то выйдет другая удивительная фигура – бутылка Кляйна, но ее нельзя сделать в обычном трехмерном пространстве.[9]

Если сгладить некоторые грани листа Мебиуса, то выйдет невозможный

треугольник Пенроуза. Это плоский треугольник-иллюзия, когда смотришь на него, он кажется объемным.[8]

Заключение

Проведя исследование, я сделал такие выводы.

Моя гипотеза подтвердилась: вокруг нас находится большое количество предметов, имеющих форму геометрических фигур. Человек в своей деятельности – при строительстве зданий, сооружений, мостов, машин использует разные геометрические формы.

Природа же подсказывает нам самые правильные варианты их применения, так как наблюдаемые людьми природные творения не просто красивы, но и детально продуманы. Человеку есть откуда черпать свои идеи, главное научиться внимательно наблюдать за природой.

Освещение информации о геометрических фигурах, изучение которых не входит в разделы познаваемые в рамках школьной программы, позволяет приобрести новые знания и иными глазами посмотреть на знакомые предметы.

Список литературы

1.Гарднер М. Математические головоломки и развлечения. — Пер. с англ. Ю.А.Данилова. — М.: Мир, 1971. — 511 с.,

2. Федер Е. Фракталы. — М: «Мир», 1991.

3. Харрис Н. Жизнь и творчество Дали.-Москва.1995

4. https://qwizz.ru/удивительные-фигуры-геометрии/

5. http://interesnik.com/geometriya-v-nashej-zhizni/

6. https://calculator888.ru/blog/raznoe/lenta-mebiusa.html

7.http://www.ntpo.com/fizika/noveyshie-issledovaniya-i-otkrytiya-v-fizike/40044-o-kolce-mebiusa-chast-1.html

8.https://calculator888.ru/blog/raznoe/lenta-mebiusa.html

9.https://ru.wikipedia.org/wiki/

Просмотров работы: 400

Геометрические фигуры и их названия

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое — все, что подскажет вам фантазия.

Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.

Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:

Геометрические фигуры 1 класс — Онлайн-тренажер

Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.

Геометрические фигуры и их названия — Проводим занятие с ребенком:

Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.

1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе — проговорит вслух названия фигур и раскрасит все картинки.
2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.
3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор — прямоугольник, часы — круг и т.д. На каждой найденной фигуре — громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.
6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.

Скачать геометрические фигуры и их названия — Бланк задания — вы можете во вложениях внизу страницы.

Названия геометрических фигур — Карточки для распечатки

Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.

Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.

После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.

Скачать названия геометрических фигур — Карточки для распечатки — вы можете во вложениях внизу страницы

Карточки для распечатки с изображением плоских геометрических фигур

С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.

Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.

Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях

Объемные геометрические фигуры и их названия — скачать карточки

В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.

Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.

Скачать — Объемные геометрические фигуры и их названия — вы можете во вложениях внизу страницы

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Рисунки из геометрических фигур — Задания в картинках и раскраски

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:

Геометрические фигуры — Раскраска для дошкольников

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Плоские геометрические фигуры — Обведи и дорисуй

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Найди формы геометрических фигур в картинках

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга — Задание для детей

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Свойства геометрических фигур для дошкольников

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Счет геометрических фигур — Картинки с заданиями

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

Чертежи геометрических тел — Задание для детей

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Геометрические фигуры из бумаги — Вырезаем и занимаемся

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.

Счет до 5 — Картинки с заданиями для малышей

Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Игра «Что лишнее? — Геометрические формы»

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.