Геометрия — Википедия

Геоме́трия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения^[1].

Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.

Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основе инвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.

Геометрия занимается взаимным расположением тел, которое выражается в прикосновении или прилегании друг к другу, расположением «между», «внутри» и так далее; величиной тел, то есть понятиями о равенстве тел, «больше» или «меньше»; а также преобразованиями тел. Геометрическое тело представляет собой абстракцию ещё со времён Евклида, который полагал, что «линия есть длина без ширины», «поверхность есть то, что имеет длину и ширину». Точка представляет собой абстракцию, связанную с неограниченным уменьшением всех размеров тела, или пределом бесконечного деления. Расположение, размеры и преобразования геометрических фигур определяются пространственными отношениями

[2].

Исследуя реальные предметы, геометрия рассматривает только их форму и взаимное расположение, отвлекаясь от других свойств предметов, таких как плотность, вес, цвет. Это позволяет перейти от пространственных отношений между реальными объектами к любым отношениям и формам, возникающим при рассмотрении однородных объектов, и сходным с пространственными. В частности, геометрия позволяет рассматривать расстояния между функциями^[1].

Классификацию различных разделов геометрии предложил Феликс Клейн в своей «Эрлангенской программе» (1872). Согласно Клейну, каждый раздел изучает те свойства геометрических объектов, которые сохраняются (инвариантны) при действии некоторой группы преобразований, специфичной для каждого раздела. В соответствии с этой классификацией, в классической геометрии можно выделить следующие основные разделы.

• Евклидова геометрия, в которой предполагается, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении.
  • Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости.
  • Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.
• Проективная геометрия, изучающая проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях.
• Аффинная геометрия, изучающая свойства фигур, сохраняющиеся при аффинных преобразованиях.
• Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.

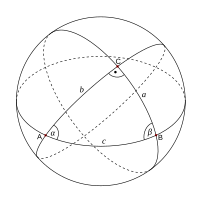Сферический треугольник

Современная геометрия включает в себя следующие дополнительные разделы.

По используемым методам выделяют также такие инструментальные подразделы.

Аксиомы евклидовой геометрии, сформулированные в III—IV веке до н. э., составляли основу геометрии до второй половины XIX века, так как хорошо описывали физическое пространство и отождествлялись с ним^[1]. Пяти постулатов Евклида было недостаточно для полного описания геометрии и в 1899 году Гильберт предложил свою систему аксиом. Гильберт разделил аксиомы на несколько групп: аксиомы принадлежности, конгруэнтности, непрерывности (в том числе аксиома Архимеда), полноты и параллельности. Позднее Шур заменил аксиомы конгруэнтности аксиомами движения, а вместо аксиомы полноты стали использовать аксиому Кантора. Система аксиом евклидовой геометрии позволяет доказать все известные школьные теоремы^[3].

Существуют и другие системы аксиом, в основе которых, помимо точки, прямой и плоскости, лежит не движение, а конгруэнтность, как у Гильберта, или расстояние, как у Кагана. Другая система аксиом связана с понятием вектора. Все они выводятся одна из другой, то есть аксиомы в одной системе можно доказать как теоремы в другой

[3].

Для доказательства непротиворечивости и полноты аксиом евклидовой геометрии строят её арифметическую модель и показывают, что любая модель изоморфна арифметической, а значит они изоморфны между собой^[4]. Независимость аксиом евклидовой геометрии показать сложнее из-за большого количества аксиом. Аксиома параллельности не зависит от других, так как на противоположном утверждении строится геометрия Лобачевского. Аналогично была показана независимость аксиомы Архимеда (в качестве координат вместо тройки вещественных чисел используется тройка комплексных чисел), аксиомы Кантора (в качестве координат вместо тройки любых вещественных чисел используются вещественные числа, построенные определённым образом), а также одной из аксиом принадлежности, которая фактически определяет размерность пространства (вместо трёхмерного пространства можно построить четырёхмерное, и любое многомерное пространство с конечным числом измерений)

[5].

Постулаты Евклида[править | править код]

Постулаты Евклида

Постулаты Евклида представляют собой правила построения с помощью идеального циркуля и идеальной линейки^[6]:

1. Всякие две точки можно соединить прямой линией;
2. Ограниченную прямую линию можно неограниченно продолжить;
3. Из всякого центра всяким радиусом можно описать окружность;
4. Все прямые углы равны между собой;
5. Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где углы меньше двух прямых.

Другая формулировка пятого постулата (аксиомы параллельности), гласит

[7]: Через точку вне прямой в их плоскости можно провести не более одной прямой, не пересекающей данную прямую.

Аксиомы евклидовой геометрии[править | править код]

В «Энциклопедии элементарной математики» предлагается следующая система аксиом^[3]:

• Аксиомы принадлежности:

1. Через каждые две различные точки проходит прямая и притом одна;
2. На каждой прямой имеется по крайней мере две точки;
3. Существуют три точки, не лежащие на одной прямой;
4. Через каждые три точки не лежащие на одной прямой проходит плоскость и притом только одна;
5. На каждой плоскости имеется по крайней мере одна точка;
6. Если две точки лежат на плоскости, то и проходящая через них прямая лежит на этой плоскости;
7. Если две плоскости имеют общую точку, они имеют по крайней мере ещё одну общую точку;
8. Существуют четыре точки, не лежащие на одной плоскости.
   • Аксиомы порядка:
9. Из любых трёх различных точек прямой одна и только одна лежит между двумя другими;
10. Для всяких двух точек прямой существует на этой прямой такая третья точка, что вторая точка лежит между первой и третьей;
11. Если прямая l, лежащая в плоскости ABC, не проходит ни через одну из точек A, B, C и содержит одну точку отрезка AB, то она имеет общую точку с хотя бы одним из отрезков AC, BC;
    • Аксиомы движения:
12. Всякое движение является взаимно однозначным отображением пространства на себя;
13. Пусть f — произвольное движение. Тогда, если точки A, B, C расположены на одной прямой, причём C лежит между A и B, то точки f(A), f(B), f(C) также расположены на одной прямой, причём f(C) лежит между f(A) и f(B);
14. Два движения, произведённые один за другим, равносильны некоторому одному движению;
15. Для всяких двух реперов, взятых в определённом порядке, существует одно и только одно движение, переводящее первый репер во второй;
    • Аксиомы непрерывности:
16. Аксиома Архимеда. Пусть A₀, A₁, B — три точки, лежащие на одной прямой, причём точка A₁ находится между A₀ и B. Пусть далее f — движение, переводящее точку A₀ в A₁ и луч A₀B в A₁B. Положим f(A₁)=A₂, f(A₂)=A₃, …. Тогда существует такое натуральное число n, что точка B находится на отрезке A_n-1A_n.
17. Аксиома Кантора. Пусть A₁, A₂, … и B₁, B₂, … — такие две последовательности точек, расположенных на одной прямой l, что для любого n точки A_n и B_n различны между собой и лежат на отрезке A_n-1B_n-1
    . Тогда на прямой l существует такая точка C, которая находится на отрезке A_nB_n при всех значениях n.
    • Аксиома параллельности:
18. Через точку A, не лежащую на прямой l, можно провести в их плоскости не более одной прямой, не пересекающей прямую l.

Если убрать из системы аксиомы 4-8, относящиеся к пространственной геометрии, то получится система аксиом евклидовой плоскости^[3].

Преобразованием множества называют его взаимно-однозначное отображение на себя. В таком смысле этот термин используется в геометрии, хотя иногда его используют и как синоним отображения или отображения множества в себя.

Говоря о «геометрических преобразованиях», обычно имеют в виду некоторые конкретные типы преобразований, играющие фундаментальную роль в геометрии — движения, преобразования подобия, аффинные, проективные, круговые преобразования (в последних двух случаях плоскость или пространство дополняют бесконечно удаленными точками). Эту фундаментальную роль выявил немецкий математик Феликс Клейн в своей лекции в университете г. Эрланген в 1872 г., известной как Эрлангенская программа. Согласно концепции Клейна, геометрия изучает свойства фигур, сохраняющиеся при всех преобразованиях некоторой группы преобразований. Рассматривая группы преобразований указанных выше видов, получают разные геометрии — евклидову (для преобразований подобия), аффинную и т. д.

Муза геометрии, Лувр

Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину^[2]. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают написанные в III веке до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом^[2]. Первые же доказательства геометрических утверждений появились в работах Фалеса и использовали, по всей видимости, принцип наложения, когда фигуры, равенство которых необходимо доказать, накладывались друг на друга^[8].

Геометрия греков, называемая сегодня евклидовой или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием. В Греции в работах Гиппарха и Менелая также появились тригонометрия и геометрия на сфере^[2].

Средние века немного дали геометрии^[1], и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода (трактат «Геометрия», 1637). Точкам пространства сопоставляются наборы чисел, это позволяет изучать отношения между геометрическими формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Систематическое изложение аналитической геометрии было предложено Эйлером в 1748 году. В начале XVII века Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии и был впервые обобщён Понселе в 1822 году. Ещё раньше, в 1799 году Монж развил начертательную геометрию, связанную напрямую с задачами черчения. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями. Дифференциальная геометрия была систематизирована Монжем в 1795 году^[2], её развитием, в частности теорией кривых и теорией поверхностей, занимался Гаусс. На стыке геометрии, алгебры и анализа возникли векторное исчисление, тензорное исчисление, метод дифференциальных форм^[1].

В 1826 году Лобачевский, отказавшись от аксиомы параллельности Евклида построил неевклидову геометрию, названную его именем. Аксиома Лобачевского гласит, что через точку, не лежащую на прямой можно провести более одной прямой, параллельной данной. Лобачевский, используя эту аксиому вместе с другими положениями, построил новую геометрию, которая в силу отсутствия наглядности, оставалась гипотетической до 1868 года, когда было дано её полное обоснование. Лобачевский, таким образом, открыл принципы построения новых геометрических теорий и способствовал развитию аксиоматического метода^[2].

Следующим шагом явилось определение абстрактного математического пространства. Проективные, аффинные и конформные преобразования, сохраняющиеся при этом свойства фигур, привели к созданию проективной, аффинной и конформной геометрий. Переход от трёхмерного пространства к n-мерному впервые был осуществлён в работах Грассмана и Кэли в 1844 году и привёл к созданию многомерной геометрии. Другим обобщением пространства стала риманова геометрия, предложенная Риманом в 1854 году^[2]. Ф. Клейн в «Эрлангенской программе» систематизировал все виды однородных геометрий; согласно ему, геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.

В 70-х годах XIX века возникла теория множеств, с точки зрения которой фигура определяется как множество точек. Данный подход позволил по новому взглянуть на евклидову геометрию и проанализировать её основы, которые подверглись некоторым уточнениям в работах Гильберта^[2].

Со времён Древней Греции в основе геометрии лежат философские понятия. Определяя точку как «то, что не имеет частей», подход к ней отличается у Пифагора, который отождествляет точку с числовой единицей и у которого точка имеет только положение в пространстве и не имеет размера, и у Демокрита, который строя атомистическую теорию, даёт точке «сверхчувственно малый» размер. К атомистическим представлениям восходят также определения линии и поверхности, где неделимыми являются «ширина» и «глубина», соответственно^[6].

Геометрия является пятым из семи свободных искусств по уровню обучения. Ей предшествует тривиум, состоящий из Грамматики, Риторики и Диалектики, а также Арифметика — старшая наука в квадривиуме, к которому также относятся Музыка и Астрономия^[9]. Марциан Капелла в своём трактате «Свадьба Философии и Меркурия» создал визуальные образы всех семи искусств и в том числе Геометрии. Искусства олицетворяли женщины с соответствующими атрибутами, которые сопровождались известными представителями сферы. Геометрия держит в своих руках глобус и циркуль, которым она может мерить, реже угольник, линейку или компасы. Её сопровождает Евклид^[10][11].

В честь геометрии назван астероид (376) Геометрия, открытый в 1893 году.

1. ↑ ^{1 2 3 4 5} Геометрия // Математическая энциклопедия : в 5 т.. — М. : Советская Энциклопедия, 1982. — Т. 1.
2. ↑ ^{1 2 3 4 5 6 7 8} БСЭ, 1971.
3. ↑ ^{1 2 3 4} Геометрия, 1963, с. 32—41.
4. ↑ Геометрия, 1963, с. 41—44.
5. ↑ Геометрия, 1963, с. 44—48.
6. ↑ ^{1 2} Геометрия, 1963, с. 12—17.
7. ↑ Геометрия, 1963, с. 18—21.
8. ↑ Геометрия, 1963, с. 12.
9. ↑ Liberal Arts (англ.). Encyclopædia Britannica. Дата обращения 20 марта 2012. Архивировано 27 мая 2012 года.
10. ↑ Семь свободных искусств (неопр.). Simbolarium. Дата обращения 20 марта 2012. Архивировано 27 мая 2012 года.
11. ↑ The Seven Liberal Arts (неопр.). Catholic Encyclopedia. Дата обращения 20 марта 2013. Архивировано 3 апреля 2013 года.

• Комацу, Мацуо. Многообразие геометрии. — М. : Знание, 1981.
• Левитин, К. Е. Геометрическая рапсодия. — 3-е изд., перераб. и доп. — М. : ИД «Камерон», 2004. — 216 с. — ISBN 5-9594-0023-5.
• Шаль, Мишель. Исторический обзор происхождения и развития геометрических методов : в 2 т.. — М. : М. Катков, 1883.
• Граве Д. А. Геометрия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Геометрия // Газлифт — Гоголево. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 6).
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. I : С древнейших времён до начала Нового времени.
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. II : Математика XVII столетия.
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1972. — Т. III : Математика XVIII столетия.
• Математика XIX века / ред. А. Н. Колмогоров, А. П. Юшкевич. — М. : Наука, 1981. — Т. 2 : Геометрия. Теория аналитических функций.
• Энциклопедия элементарной математики / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Физматгиз, 1963. — Кн. 4 : Геометрия. — 568 с.
• Энциклопедия элементарной математики / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Наука, 1966. — Кн. 5 : Геометрия. — 624 с.

Геометрия: уроки, тесты, задания.

Аксиомы стереометрии

1. Аксиомы стереометрии и их простейшие следствия

Параллельность прямых и плоскостей

1. Параллельность прямых, прямой и плоскости

2. Взаимное расположение прямых в пространстве. Угол между прямыми

3. Параллельность плоскостей

4. Тетраэдр и параллелепипед

Перпендикулярность прямых и плоскостей

1. Перпендикулярность прямой и плоскости

2. Перпендикуляр и наклонные. Угол между прямой и плоскостью

3. Двугранный угол. Перпендикулярность плоскостей

Многогранники

1. Понятие многогранника. Призма

2. Пирамида

3. Правильные многогранники

Векторы в пространстве

1. Понятие вектора в пространстве

2. Сложение и вычитание векторов. Умножение вектора на число

3. Компланарные векторы

Удивительные геометрические фигуры

Геометрия – точная математическая наука, которая занимается изучением пространственных и других подобных отношений и форм. Но ее часто называют «сухой», поскольку она не способна описать форму многих природных объектов, ведь облака – это не сферы, горы – не конусы, а молнии распространяются не по прямым линиям. Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.

Тем не менее, существует ряд удивительных фигур, которые обычно не изучаются на школьных уроках геометрии, но именно они окружают человека в реальном мире: в природе и архитектуре, головоломках, компьютерных играх и т. д.

Фрактал

Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.

При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными. Его придумал в 1975 г. Бенуа Мандельброт, позаимствовав латинское слово «fractus» (ломанный, дробленный).

Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.

Лента Мебиуса

Это одна из самых необыкновенных трехмерных фигур в геометрии, которую легко сделать в домашних условиях. Для этого достаточно взять бумажную полоску, ширина которой в 5-6 раз меньше ее длины, и, перекрутив один из концов на 180°, склеить их между собой.

Если все сделано правильно, то можно проверить самостоятельно ее удивительные свойства:

• Наличие только одной стороны (без разделения на внутреннюю и внешнюю). Это легко проверить, если попробовать закрасить карандашом одну из ее сторон. Независимо от того, в каком месте и направлении будет начато закрашивание, в результате вся лента будет закрашена одним цветом.
• Непрерывность: если вести ручкой линию вдоль всей поверхности, ее конец соединится с начальной точкой без пересечения границ поверхности.
• Двухмерность (связность): при разрезании ленты Мебиуса вдоль она остается цельной, просто получаются новые фигуры (к примеру, при разрезании надвое получится одно кольцо большего размера).
• Отсутствие ориентированности. Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.

Лента Мебиуса широко используется в промышленности и науке (в ленточных конвейерах, матричных принтерах, механизмах для заточки и пр.). Кроме этого существует научная гипотеза, по которой сама Вселенная также представляет собой ленту Мебиуса невероятных размеров.

Полимино

Это плоские геометрические фигуры, которые образуются за счет соединения нескольких квадратов равных размеров по их сторонам.

Названия полимино зависят от количества квадратов, из которых они сформированы:

• мономино – 1;
• домино – 2;
• тримино – 3;
• тетрамино – 4 и т. д.

При этом для каждой разновидности существует разное количество типов фигур: у домино 1 тип, у тримино – 3 типа, у гексамино (из 6 квадратов) – 35 типов. Число различный вариаций зависит от количества используемых квадратов, но при этом еще никому из ученых не удалось найти удивительную формулу, которая будет выражать эту зависимость. Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.

Полиамонд

Наряду с полимино, существует еще одна удивительная геометрическая фигура, используемая для составления других фигур – полиамонд. Он представляет собой многоугольник, сформированный из нескольких равносторонних треугольников равного размера.

Название придумал математик Т. О’Бейрн на основании одного из названий ромба в английском языке – диамонд, который можно составить из 2-х равносторонних треугольников. По аналогии, фигуру из 3-х равносторонних треугольников О’Бейрн назвал триамондом, из 4-х – тетриамондом и т. д.

Главным вопросом их существования остается вопрос о возможном количестве полиамондов, которые можно составить из определенного количества треугольников. Применение полиамондов в реальной жизни также аналогично использованию полимино. Это могут быть разного рода головоломки и логические задачи.

Треугольник Рело

Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.

Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:

• сверла Уаттса, которое позволяет сверлить отверстия практически идеальной квадратной формы, только с чуть закругленными краями;
• медиатора, необходимого для игры на музыкальных щипковых инструментах;
• кулачковых механизмов, используемых для создания зигзагообразных швов в швейных машинах, а также немецких часах;
• стрельчатых арок, характерных для готического стиля в архитектуре.

Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:

Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.

Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей». На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.

Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.

Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.

 

Ответы@Mail.Ru: Интересные факты о геометрии

Интересные факты о геометрии: ============================== -Древнегреческий ученый Эратосфен по законам геометрии нашел длину экватора Земли. Заметив, что когда Солнце находится в зените в Сиене (Африка), то в Александрии расположенной на 800 м, оно отклоняется на 7 градусов. Ученый установил, что длина экватора равна: 360 / 7 * 800 = 41 140 (км) -Будучи в престарелом возрасте английский математик Абрахам де Муавр однажды обнаружил, что продолжительность его сна с каждым днем растет на 15 минут. Составив геометрическую прогрессию, Абрахам определил дату своей смерти. Это была дата — 27 октября 1754 года, сон достиг 24-х часов.. -Треугольник Рело — это геометрическая фигура, сформированная пересечением трех равных кругов радиуса «а» с центрами в вершинах равностороннего треугольника со стороной а. Сверло, изготовленное на основе такого треугольника Рело, позволяет сверлить квадратные отверстия с погрешностью в 2%. -Различные утверждения в геометрии о сумме углов треугольника: у Лобачевского &lt; 180 градусов; у Евклида = 180 градусов; у Римана &gt; 180 градусов. -Формула вычисления объема усеченной пирамиды выведена раньше, чем формула для целой пирамиды. -Библия геометрии – это книга «Начала» Евклида. В общем-то, это не книга, а набор папирусов. Именно в них впервые он изложил непреложные истины, которые мы называем аксиомами геометрии. В общей сложности лично им было доказано 465 теорем. Источник: <a rel=»nofollow» href=»http://selfhacker.net/universe/interesnye-fakty-o-geometrii.html» target=»_blank»>Интересные факты о геометрии | SelfHacker</a>

<a href=»/» rel=»nofollow» title=»15907216:##:1STErLe»>[ссылка заблокирована по решению администрации проекта]</a>

Факт №8: В Англии таблица Пифагора имеет размерность не 10 на 10, а 12 на 12. Факт №7: Арабские числа на самом деле не арабские, они были изобретены в Индии. Факт №6: Самое большое число, имеющее название — центильон. Это единица с 600 нулями. Оно было записано в 1852 году. Факт №5: В геометрии существует всего пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Факт №4: Если число 111 111 111 помножить на себя самого, то получится интересное число 12 345 678 987 654 321 (все числа сначала возрастают, а потом убывают попорядку). Факт №3: В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180. В геометрии Римана сумма углов треугольника всегда больше 180. Факт №2: 1001 — наименьшее четырёхзначное число, являющееся суммой двух кубов натуральных чисел. Факт №1: Если сложить все числа, нанесённые на колесо рулетки для казино, то получится магическое число 666.

акакакакакакакакакакакакакакакакакакак

Урок 1: Что такое геометрия?

План урока:

Знакомство с геометрией

Основные понятия геометрии

Сравнение отрезков и углов

Виды углов

Перпендикулярные и параллельные прямые

Интересные сведения о геометрии

 

Знакомство с геометрией

Вот и настал момент прощания с математикой, сопровождающей нас на протяжении долгих шести лет школьной жизни. Но огорчаться не нужно, на смену привычной математике приходят занимательные и интересные разделы этой науки – алгебра и геометрия.

Давайте разберемся, что же такое геометрия, для чего она нужна, где её используют?

В дословном переводе с греческого, геометрия означает землемерие:

 

Более точное определение утверждает, что наука об отношениях плоскостей, пространств и изучении форм называется геометрией.

Постоянно сталкиваясь с геометрией не придаем этому большого значения. Она всегда рядом, она живет с нами. Оглянитесь вокруг – потолок, стены, мебель, бытовая техника отображают геометрические фигуры, созданные с учетом геометрических знаний. Выйдя на улицу, посмотрите по сторонам – стволы деревьев и стебли растений имеют цилиндрическую форму, кроны деревьев — форму конусов, овалов, треугольников, лепестки цветов — форму круга или овала. Любая профессия (хирург, строитель, водитель, учитель, повар) имеет связь с основами геометрии. Повсюду нас окружают геометрические элементы. Эта наука плотно вошла в нашу жизнь, и является её неотъемлемой частью.

Геометрия содержит ряд основных понятий, необходимых для дальнейшего изучения и применения на практике геометрических знаний. Давайте познакомимся с ними поближе.

 

Основные понятия геометрии

Понятие точки

Фигура, которую невозможно измерить, а для вычислений используется только место её расположения, называется точкой. Такие фигуры обозначают цифрами и буквами латиницы. Если точек много, то обозначения должны быть разными.

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

Читается: точка A, точка B, точка C

 

Понятие линии

Линия представляет собой массу точек. Линии принято обозначать строчными буквами латиницы.

Например:

Линии бывают:

1. Прямые

 

2. Ломаные

 

3. Кривые

 

Часто в геометрии используются прямые линии. Давайте подробнее с ними познакомимся.

По определению, бесконечная линия, не имеющая ограничений, называется прямой. Обозначается маленькими и большими (выбирая 2 любые точки) буквами латиницы.

Например:

Читается: прямая а, прямая AD

 

Любые две точки на прямой ограничивают геометрическую фигуру – отрезок. Эти точки называются началом и концом отрезка. Фигура обозначается большими буквами латиницы.

Например:                                                                                                               

Читается: отрезок КВ, отрезок АС

 

Наличие точек дает возможность измерить длину. Длиной отрезка принято считать расстояние между точками, обозначающими начало и конец.

Например:

Расстояние между точками А, В равняется 7 сантиметрам. Считается, что отрезок АВ по длине соответствует 7 сантиметрам.

Записывается следующим образом: АВ=7см

 

Понятие луча

Рассматривая понятие луч, делаем вывод, что любая точка, лежащая на прямой, делит её на лучи. Сама точка называется началом лучей. Обозначаются большими буквами латиницы.

Например:

Читается: точка В разделяет прямую а на два луча

 

Чтобы определить нужный луч, на прямую необходимо нанести дополнительные точки.

Например:

Читается: точка А делит прямую с на два луча: луч А, луч АВ

 

Необходимо учитывать, что при записи обозначения луча на первом месте должна находиться буква, обозначающая начало луча.

 

Понятие угла

Геометрическая фигура, состоящая из точки и выходящих из неё двух лучей, называется углом. Лучи называют сторонами угла, а точку – вершиной угла.

Обозначается угол специальным знаком∠, также заглавными буквами латиницы, прописными греческими, цифрами.

Например

      

Записывается и читается: ∠ВАС (название вершины угла, обязательно записывается в середине) – угол ВАС, ∠β – угол бета

Для определения меры углов используется единица измерения – градус. Полный оборот луча вокруг своего начала составляет 360˚, значит, 1 градус равен 1/360. Для обозначения градуса существует специальный символ ˚.

 

Сравнение отрезков и углов

В этом разделе, как и во всех разделах математики, существует понятие сравнения. Две фигуры с идентичными размерами и формой называются равными. Самым простым методом нахождения равенства геометрических фигур является способ наложения. Рассмотрим этот метод сравнения поподробнее.

Правило определения равенства геометрических фигур методом совмещения имеет следующую формулировку: геометрические фигуры, полностью совмещенные наложением друг на друга, считаются равными.

Сравнение отрезков.

Для сравнения отрезков методом совмещения, необходимо начало отрезка наложить на начало другого отрезка, если при этом совпадут и концы, то тогда отрезки считаются равными.

Например:

На рисунке видно, что начало отрезка АВ совпадает с началом отрезка СМ, при этом совпадают и концы отрезков. Такие отрезки считаются равными АВ=СМ.

В случае, когда концы отрезков не совпадают, считается, что один отрезок больше другого.

Например

При наложении отрезка СР на отрезок ВК совпадают только начала отрезков. В таком случае отрезок ВК больше, чем отрезок СР.

Записывается в таком виде: ВК>СР или СР<ВК.

Важно помнить, что каждый отрезок имеет точку, делящую его на две равные части и называющуюся серединой отрезка.

Например:

Точка В является серединой отрезка АС, поэтому АВ=ВС

А как же метод наложения используется при сравнении углов? Все очень просто!

В случае с углами достаточно наложить вершины углов и любую из сторон, если при этом получается наложенным весь угол, то такие углы называют равными.

При наложении угла 2 на угол 1 на первом рисунке, совпадают вершины, стороны угла, такие углы называют равными.

Записывается в таком виде: ∠1=∠2.

В случае, когда стороны не совпадают, один угол считается больше второго, ∠2>∠1 или∠1<∠2

На втором рисунке видно, что вершина и сторона угла совпадают при наложении, а вторые стороны угла не совпадают. Тогда считается, что угол 2 больше, чем угол1.

Записывается в таком виде:∠2>∠1

 

Виды углов

С углами, отрезками и методом сравнения без использования вычислений мы познакомились. Теперь давайте узнаем, какие бывают виды углов в зависимости от градусной меры.

• Острый. Градусная мера <90 ˚

 

• Прямой. Градусная мера =90 ˚

 

• Тупой. Градусная мера >90 ˚

 

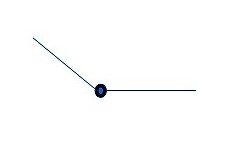
• Развернутый. Градусная мера =180 ˚. Развернутый угол, состоит из двух прямых углов.

 

Когда углы дополняют один другого, то они могут быть смежными углами и вертикальными углами.

Смежные углы – углы, у которых есть общая сторона, а из оставшихся сторон получается прямая линия.

Например:

Углы ∠ АСР и ∠РСВ являются смежными, так как сторона СР одна на двоих, а из сторон АС, СВ получается прямая линия. Сумма смежных углов равна 180 ˚.

Если стороны углов продолжают друг друга, составляя при этом прямые линии,то эти углы вертикальные.

Например:

Лучи углов 1 и 2 составляют прямые, поэтому они являются вертикальными, как и углы 3, 4.

Помните! Всегда вертикальные углы равны между собой: ∠1=∠2, ∠3=∠4.

Зная, что такое угол, из каких фигур он состоит,сделаем предположение, что из вершины угла можно провести большое количество лучей, но только один луч обладает интересным свойством – делит угол на два одинаковых угла и называется биссектрисой.

Делаем вывод, что биссектриса – луч, выходящий из вершины угла и делящий его ровно пополам. Основным свойством такого луча является равноудаленность от сторон угла всех точек, лежащих на нем.

Например:

Рассмотрим развернутый угол АСВ. Из вершины С проведем луч СМ, делящий его на два одинаковых угла – это и будет биссектриса. Каждая точка, лежащая на биссектрисе, находится на равном расстоянии от сторон угла.

 

Перпендикулярные и параллельные прямые

И наконец, узнаем про перпендикулярные и параллельные прямые.

Важно помнить, что прямые либо пересекаются в одной общей точке, либо не пересекаются вообще.

Когда прямые при пересечении образуют угол 90˚ их называют перпендикулярными прямыми.

Например:

 

Записывают: а⊥b

Если прямые никогда не пересекаются на плоскости, то их называют параллельными.

Например:

Прямые а, b – параллельны. Записывается: а||b

 

Интересные сведения о геометрии

• Египет стал родиной геометрии 4000 лет назад. Геродот, живший 2500 лет назад, в своих трудах указывал, что при дворе царя находились специальные люди, называющиеся геометрами. В их обязанности входило измерение земель жителей для дальнейшего начисления налога. Река Нил постоянно заливала земельные наделы, а для правильного расчета налога нужно использовать точные размеры участка. Поэтому геометры были востребованными и уважаемыми людьми.
• Для древних людей большое значение имела форма окружающих вещей. Благодаря различиям форм и цвета люди отличали вкусные дары природы от невкусных (грибы, ягоды, корневища), хорошую древесину для изготовления различных изделий от непригодной и так во всех сферах жизни. Редким лакомством были кокосы, которые имели форму шара. Кристаллы соли представляли в виде куба. Так ежедневно, в домашних хлопотах, человечество постигало науку геометрию.
• Имеется научное подтверждение, что двести тысяч лет назад уже использовались предметы различных форм, напоминающие геометрические фигуры. Названий фигур люди не знали, использовали сравнительные характеристики: такая, как солнце, такое, как ягода.                           
• При строительстве первых деревянных домов древние люди стали все глубже разбираться в геометрии: как сделать ровные и одинаковые стены, крышу правильной формы, необходимые размеры, формы строительного материала. Бессознательно население изучало геометрию: женская часть кроила и шила носильные вещи, мужчины изготавливали копья, бумеранги сложных геометрических форм.

 
(источник)

 

Геометрия в природе — животные, растения, ландшафт и другое

Природа — самый гениальный архитектор, создающий правильные и совершенные формы, которые подчас бывают столь безупречны, что невозможно поверить в их реальное существование. Геометрия в природе проявляется во всём.

Животные

Понаблюдайте за животными. В большинстве своём их формы гармоничны. Равно как и у человека, в теле зверей всегда присутствует строгая симметрия.

Рассмотрим симметрию на примерах только нескольких животных.

Растения

Формы растений порой бывают такой причудливой геометрии, что завораживают взгляд.

Посмотрите, какая правильная геометрия и овальность форм у обычной красной капусты в разрезе.

А вот ещё несколько примеров.

Ландшафт

Природный ландшафт веками формируется за счёт эрозий, движений ледников и тектонических плит. Его конфигурации и цвета гармоничны и плавно перетекают из одной в другую.

Особенно хорошо это видно на фотографиях, сделанных со спутника.

Планеты

Присутствует геометрия и в космосе.

Здесь её законам подчиняются планеты и их спутники.

Все они шарообразной формы и вращаются вокруг своей оси и Солнца.

Геометрия природных объектов очень разнообразна и порой приобретает самые причудливые и неожиданные формы. Они вызывают восхищение и радуют глаз.

Интересные факты о треугольниках | KtoiKak.com

Интересные факты о треугольниках

Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов. Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.

Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности. Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.

* Китайцы гордятся китайским треугольником и считают, что он есть первоначалом всех фигур, и все остальные фигуры — лишь его частные случаи.

Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.

А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.

А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.

Первая буква большого числа алфавитов. Имеет финикийское происхождение и, чаще всего изображается в виде перевернутого треугольника. Числовое значение — единица.

Треугольник Рёло — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса a с центрами в вершинах равностороннего треугольника со стороной a. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с неточностью в 2%).