No birds: Развитие PageRank

С того момента, когда PageRank был впервые представлен в 1998 году, было потрачено немало усилий, чтобы улучшить его качество и скорость вычисления. В этой обзорной и достаточно популярной статье я опишу основные направления исследований вокруг PageRank и варианты алгоритма.

Я разрабатываю систему оценки важности web-страниц на основе входящих и исходящих ссылок в компании Нигма, поэтому смотрю на PageRank с математической стороны, со стороны разработчика а не seo.

Я не буду пересказывать здесь многократно описанные основы PageRank. Предполагается, что читатель знает, что это вообще такое. Если же нет, то для начала могу порекомендовать статью Растолкованный PageRank.

На следующей картинке схематически представлены основные направления исследований, окруживших PageRank. Каждому овалу на схеме будет соответствовать отдельная глава статьи.

PageRank с математической стороны

PageRank основан на математической модели случайного блуждания «пользователя» в сети интернет. В некоторый момент он находится на одной странице, затем случайным образом выбирает одну из ссылок и переходит по ней на другую. «Пользователь» произвольно выбирает ссылки, не отдавая предпочтение каким-либо из них.

PageRank страницы – это вероятность того, что блуждающий «пользователь» находится на данной странице.

Сделаем небольшой набросок того, как рассчитать эту вероятность.

Пронумеруем web-страницы целыми числами от 1 до N.

Сформируем матрицу переходов P, содержащую вероятность перехода «пользователя» с одной страницы на другую. Пусть deg(i) – количество исходящих ссылок на странице i. В таком случае, вероятность перехода со страницы i на страницу j равна:

P[i, j] = 1 / deg(i), если i ссылается на j
P[i, j] = 0, если i не ссылается на j

Пусть p^(k) – это вектор, содержащий для каждой страницы вероятность того, что в момент k на ней находится «пользователь». Этот вектор – распределение вероятностей местоположения «пользователя».

Предположим, что «пользователь» может начать своё бесцельное блуждание с любой страницы. То есть, начальное распределение вероятностей равномерно.

Зная распределение вероятностей в момент k, мы можем узнать распределение вероятностей в момент k+1 по следующей формуле:

В основе этой формулы не более чем правила сложения и умножения вероятностей.

Математически мы пришли к цепи Маркова с матрицей переходов P, где каждая web-страница представляет собой одно из состояний цепи.

Но нам нужно знать вероятность нахождения «пользователя» на странице независимо от того, сколько шагов k он сделал от точки начала блуждания.

Мы берём начальное распределение вероятностей p⁽⁰⁾. Считаем по представленной выше формуле распределение p⁽¹⁾. Затем по той же формуле считаем p⁽²⁾, затем p⁽³⁾ и т.д. до тех пор, пока некие p^(k-1) и p^(k) не будут отличаться лишь незначительно (полное равенство будет достигнуто при k стремящемся к бесконечности).

Таким образом, последовательность p⁽¹⁾, p⁽²⁾, p⁽³⁾ … сойдётся к некому вектору p = p^(k). Интересно, что вектор p на самом деле не зависит от начального распределения (т.е. от того, с какой страницы начал своё блуждание воображаемый «пользователь»).

Вектор p таков, что в любой момент (начиная с некоторого момента k), вероятность того, что «пользователь» находится на странице i, равна p[i]. Это и есть искомый PageRank.

Этот алгоритм называется методом степеней (power method). Он сойдётся только в том случае, если выполняются два условия: граф страниц должен быть сильно связным и апериодическим. Как достигается выполнение первого условия, будет рассмотрено далее. Второе же без дополнительных усилий справедливо для структуры web.

Примечание

При выполнении условий сильной связности и апериодичности, согласно эргодической теореме, цепь Маркова с матрицей перехода P имеет единственное стационарное распределение p:

PageRank и является стационарным распределением цепи Маркова.

Также это выражение представляет собой собственную систему, а вектор p — собственный вектор матрицы A. Поэтому и применяется метод степеней — численный метод для поиска собственных векторов.

Висячие узлы (dangling nodes)

Висячие узлы – это страницы, которые не имеют исходящих ссылок. Страница может не иметь исходящих ссылок просто потому, что у неё их нет, либо потому, что она не была прокраулена (crawled) – т.е. страница попала в базу, т.к. на неё ссылаются другие прокрауленные страницы, но сама прокраулена не была, и о её исходящих ссылках ничего не известно.

Для вычисления PageRank в графе страниц не должно быть висячих узлов. Сумма каждого ряда матрицы переходов должна быть равна единице (row-stochastic), для висячих же узлов она окажется равной 0 – входные данные алгоритма будут некорректными.

По статистике, даже если поисковая система имеет достаточно большой индекс, 60% страниц оказывается висячими. Поэтому то, как с ними поступать, оказывает большое влияние на ранжирование.

Метод удаления

Изначальный подход, предложенный Пэйджем, заключается в том, чтобы удалить висячие узлы перед вычислением PageRank.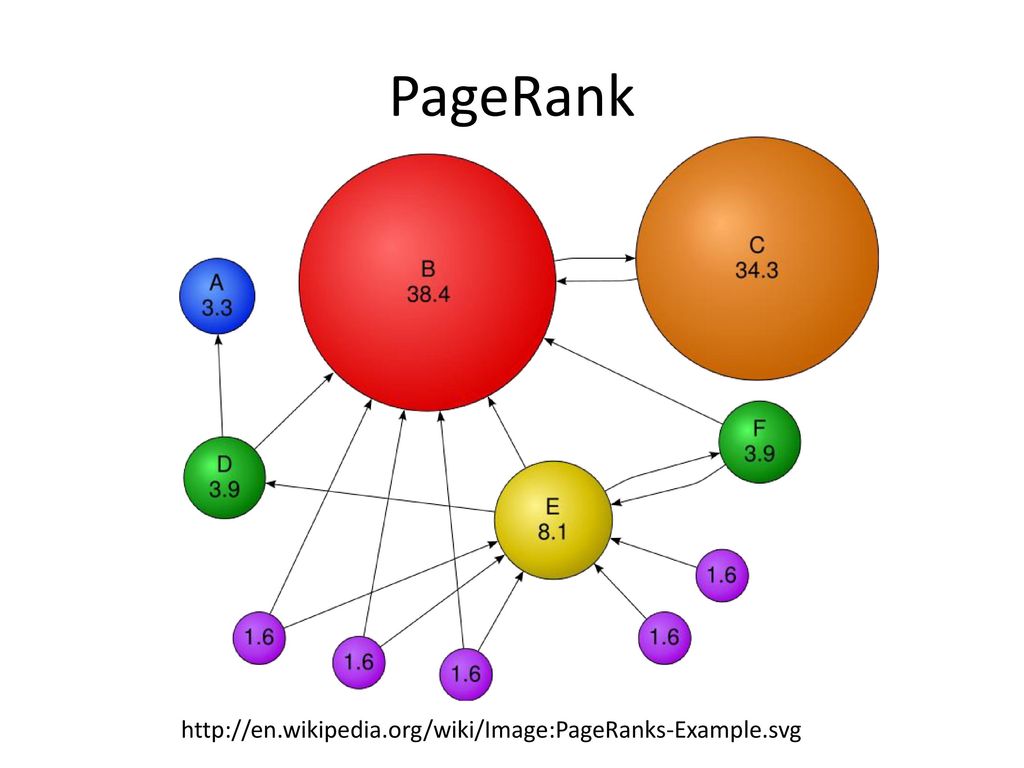 В качестве обоснования предлагается то, что висячие узлы не оказывают влияния на другие страницы. Но это не совсем так – удаляя их, мы уменьшаем количество исходящих ссылок страниц, которые на них ссылаются. Тем самым мы увеличиваем значение PageRank, которое эти страницы передают через свои ссылки.

Кроме того, удаление висячих узлов, может создать новые висячие узлы. Таким образом, требуется проделать несколько итераций удаления (обычно 5 или что-то около того).

В качестве развития этого подхода, было предложено после вычисления PageRank возвращать удалённые узлы назад в граф и проделывать ещё столько же итераций алгоритма PageRank, сколько было проделано итераций удаления. Это позволяет получить значение PageRank и для висячих узлов.

Считать связанными со всеми другими страницами

Наиболее популярный трюк заключается в том, чтобы считать висячие узлы связанными со всеми другими страницами. В модели случайного блуждания данный метод находит подходящее объяснение: попав на страницу без исходящих ссылок, «пользователь» перескакивает на любую другую страницу сети случайным образом.

Можно считать вероятность попадания «пользователя» на страницу из висячего узла в результате такого перескока распределённой равномерно среди всех страниц сети. Но можно и не считать её таковой. Например, можно исключить попадание из висячего узла на другой висячий узел. Или распределить вероятность между страницами по аналогии с аристократическим вектором телепортации, о котором будет рассказано ниже в главе Телепортация.

Матрица переходов модифицируется следующим образом:

d[i] = 1, если i – висячий узел, и 0 в противном случае
v[j] – вероятность попадания «пользователя» на страницу j из висячего узла

Шаг назад (step back)

Проблему висячих узлов можно решить, добавив каждому такому узлу обратные ссылки на страницы, которые на него ссылаются. В модели блуждания это соответствует нажатию кнопки назад в браузере «пользователем», попавшим на страницу без исходящих ссылок. Этот метод критикуют за то, что он поощряет страницы с большим количеством ссылок на висячие узлы. Однако в некоторых моих экспериментах такой подход давал лучшее ранжирование.

Петля (self-link)

Упомяну кратко ещё один способ. Каждому висячему узлу можно добавить ссылку на самого себя – это приведёт в порядок матрицу переходов. Но после вычисления PageRank, результат придётся определённым образом скорректировать. Подробности описаны в G. Jeh and J.Widom “Scaling Personalized Web Search.”

Телепортация

Решение проблемы висячих узлов ещё не даёт сильную связность графа. Поэтому вводится телепортация.

В модели случайного блуждания это выглядит так: «пользователь», находясь на некоторой странице, с вероятностью c переходит по одной из её ссылок и с вероятностью (1 – c) * v[j] перескакивает (телепортируется) на страницу j. Стохастический вектор v описывает вероятность телепортации на ту или иную страницу и называется вектором телепортации.

c как правило выбирается в диапазоне 0.85 – 0.9. Большие значения дают более точные результаты, но более медленную сходимость. Меньшие значения – быструю сходимость, но менее точные результаты.

Плюс ко всему, чем меньше значение с, тем больше возможностей для поискового спама – достаточно создать на сайте огромное количество страниц и они будут, как зонтик, собирать значительный PageRank, получаемый за счёт телепортации.

Существует два способа выбора вектора телепортации: демократический и аристократический. Демократический вектор содержит одинаковые значения вероятности для всех страниц. Это стандартный вариант. Аристократический содержит низкую вероятность для обычных страниц и более высокую для избранных достоверно качественных неспамерских страниц. Последний способ явно поощряет избранные страницы в ущерб остальным, зато более устойчив к поисковому спаму.

В одной из статей предлагалось делать более высокую вероятность телепортации для главных страниц сайтов, но мне не известно, каковы были результаты.

Значение v[j] не должно быть равно 0. Иначе может оказаться, что j недосягаема из некой другой страницы, что означает нарушение сильной связности.

Телепортация модифицирует матрицу переходов следующим образом:

v – вектор телепортации

Мы ещё вернёмся к вектору телепортации, когда будем обсуждать персонализацию PageRank.

Ускорение метода степеней

Многие исследователи пытались ускорить сходимость метода степеней. Посмотрим на самые удачные способы.

Для удобства повторю формулу, которую мы используем на каждой итерации. Назовём её формулой А:

Метод Гаусса-Зейделя (Gauss-Seidel method)

На каждой итерации в методе степеней мы используем значения элементов вектора p^(k) чтобы рассчитать вектор p^(k+1). Отличие метода Гаусса-Зейделя в том, что мы сразу используем значения вычисленных элементов вектора p^(k+1) для вычисления его остальных элементов.

В методе Гаусса-Зейделя мы последовательно элемент за элементом вычисляем вектор p^(k+1). При это там где, согласно формуле А, нам нужно использовать значение p^(k)[i] мы используем p^(k+1)[i], если этот элемент вектора уже был вычислен.

Согласно экспериментам этот метод способен сократить необходимое количество итераций на 40%. Его недостаток в том, что его достаточно сложно вычислять параллельно.

Методы экстраполяции (Extrapolation methods)

В этой группе методов мы проделываем некоторое количество d обычных итераций метода степеней. Затем на основе результатов этих итераций строим аппроксимацию решения и используем её вместо p^(k) для следующей итерации. Через следующие d итераций повторяем трюк. И так далее пока алгоритм не сойдётся.

Исследователям удавалось достичь сокращения необходимого количества итераций на 30%.

Адаптивный метод (Adaptive method)

Этот метод основан на наблюдении, что значительная часть элементов вектора p сходится гораздо быстрее остальных и затем почти не меняется. Ускорение в этом методе достигается за счёт того, что мы не пересчитываем значения таких элементов.

Если в какой-то момент k для некоторого элемента i обнаруживается что p^(k+1)[i] — p^(k)[i] меньше определённого порога, мы считаем, что значение PageRank для страницы i найдено и более не пересчитываем i-тый элемент вектора p.

Исследователям удавалось достичь сокращения времени работы метода степеней на 20% при помощи этого трюка.

Однако данный метод требует периодически переупорядочивать данные, чтобы избежать вычисления тех элементов, значения которых считаются уже найденными. Поэтому адаптивный метод плохо подходит для больших графов – переупорядочить огромный объём данных становится слишком дорогой задачей.

Метод блочной структуры (Block Structure Method)

Web имеет блочную структуру. Это открытие столь интересно, что я намерен посвятить ему отдельный пост. Там же и обсудим этот метод.

UPD: пост о блочной структуре web.

Численные методы

Вычисляя значение PageRank, мы ищем такой вектор p, что

Это выражение является так называемой собственной системой, а p – собственный вектор матрицы A. Задача поиска собственного вектора может быть представлена системой линейных уравнений. В нашем случае это будет огромная, но всё же обычная система, которая может быть решена при помощи численных методов линейной алгебры.

Тем не менее, вычисление PageRank численными методами ещё находится в экспериментальной области. Каковы будут характеристики и свойства этих методов на реальных графах web пока не понятно.

Стоит отметить, что существуют уже готовые решения для параллельного вычисления крупных линейных систем.

Параллелизация

Вычисление PageRank параллельно на нескольких машинах позволяет существенно ускорить работу.

По сути методы параллелизации можно разделит на два типа.

Первые разделяют граф страниц на плотно связные компоненты – группы страниц плотно связанных ссылками между собой и имеющие относительно немного ссылок на страницы вне группы. PageRank для каждой такой группы вычисляется параллельно. Процессы/потоки периодически обмениваются информацией, когда дело доходит до ссылок между страницами разных групп.

Ко второму типу относятся методы, использующие блочную структуру web. О них мы поговорим в уже обещанном выше посте о блочной структуре.

UPD: пост о блочной структуре web.

Оптимизация ввода-вывода

Это довольно интересная тема, которую я приберегу для одного из следующих постов. Я представлю три алгоритма, которые будут интересны не только с точки зрения вычисления PageRank, но и вообще с точки зрения обработки больших объёмов информации.

Эволюция графа

Довольно естественной кажется идея не пересчитывать PageRank для всех страниц целиком, а найти способ обновлять его по мере эволюции графа страниц (по мере эволюции web).

В «Incremental Page Rank Computation on Evolving Graphs» Prasanna Desikan и др. предлагают следующий способ.

Сперва выделить часть графа, состоящую из страниц, до которых не существует путей от новых страниц, исчезнувших страниц, либо страниц, ссылки которых были изменены. Удалить эту часть графа, оставив только граничные узлы (т.к. они влияют на PageRank оставшихся страниц). Посчитать PageRank для оставшегося графа. Затем отмасштабировать значения PageRank с учётом общего количества страниц – т.к. количество страниц влияет на часть PageRank, получаемую за счёт телепортации.

Замечу, что полученный в результате PageRank не является точным, а всё же некой аппроксимацией.

По различным данным от 25% до 40% ссылок между web-страницами меняются в интернет в течение недели. Такая скорость изменения, на мой взгляд, оправдывает полный пересчёт PageRank всех страниц.

Персонализация

Представление о важности той или ной страницы во многом субъективно. То, что покажется одному отбросом, другой сочтёт изумрудом. Пусть есть очень качественная страница об игре керлинг, но я совершенно не хочу, чтобы она вылезала лично мне в топ. Чтобы учитывать в ранжировании интересы конкретного человека был придуман персонализированный PageRank.

Выбирается какое-то количество категорий, по которым можно классифицировать тематику тех или иных страниц (или сайтов). Например: культура, спорт, политика и т.п.

Пусть T[j] – множество страниц, принадлежащих к категории j (или расположенных на сайте, принадлежащем к данной категории).

Для каждой категории формируется особый вектор телепортации v (см. главу Телепортация).

v[i] очень мало, если страница i не принадлежит T[j], и значительно больше если принадлежит.

Для каждого тематического вектора телепортации вычисляется тематический PageRank p_j. Вычислить сто тематических PageRank для ста категорий вполне реально.

Допустим, у нас есть вектор k, сумма элементов которого равна единице. Значение k[j] отражает степень заинтересованности пользователя (реального, а не того из модели блуждания) в категории j.

Степень заинтересованности пользователя может быть указана явно, или она может быть сохранена в его профиле. Или она может быть выведена исходя из того, какие слова входят в запрос. Например, если запрос содержит слово fairtrade то можно вывести, что пользователь заинтересован на 0.4 в теме общество, на 0.4 в теме экономика и на 0.2 в теме политика.

Во время ранжирования результатов запроса пользователя для страниц используется следующее итоговое значение PageRank:

k[0] * p₀ + k[1] * p₁ + … + k[n] * p_n , где n – количество категорий

Таким образом, рейтинг страницы будет зависеть от того, что реально интересно пользователю.

Темы, которые будут рассмотрены в следующих постах

Оптимизация ввода-вывода

Это довольно интересная тема, которую я приберегу для одного из следующих постов. Я представлю три алгоритма, которые будут интересны не только с точки зрения вычисления PageRank, но и вообще с точки зрения обработки больших объёмов информации.

Siterank

UPD: Эта тема освещена в посте о блочной структуре web.

SiteAnalyzer — описание проверяемых параметров SEO-аудита

В таблице ниже указаны описания всех проверяемых параметров и выявляемых ошибок в разделе «Статистика SEO».

Группа / Параметр	Описание	?
Изображения
Битые изображения	Показывает недоступные изображения (разрыв соединения с сервером, превышение времени ожидания ответа и т.п.) или изображения, которые возвращают код ответа сервера 4xx и 5хх	x
Изображения без атрибута ALT	Показывает страницы, содержащие изображения с отсутствующим или пустым атрибутом ALT	~
Изображения без атрибута TITLE	Показывает страницы, содержащие изображения с отсутствующим или пустым атрибутом TITLE	i
Макс. размер изображения	Показывает адреса изображений, размер которых превышает [200] Кбайт (определяется по HTTP-заголовку Content-Length). Данный параметр является настраиваемым и его можно поменять в настройках программы, вкладка «SEO»	~
Ссылки
Битые ссылки	Показывает недоступные URL (разрыв соединения с сервером, превышение времени ожидания ответа и т.п.) или адреса страниц, которые возвращают код ответа сервера 4хх и 5xx	x
Страницы без входящих ссылок	Показывает страницы, на которые не ведет ни одной внутренней ссылки	x
Страницы без исходящих ссылок	Показывает страницы, с которых не ведет ни одной исходящей ссылки (учитываются только внутренние ссылки текущего проекта)	x
Внутренние nofollow ссылки	Показывает страницы, содержащие исходящие внутренние ссылки с атрибутом rel=»NOFOLLOW»	i
Внешние nofollow ссылки	Показывает страницы, содержащие исходящие внешние ссылки с атрибутом rel=»NOFOLLOW»	i
Внешние dofollow ссылки	Показывает страницы, содержащие исходящие внешние ссылки без атрибута rel=»NOFOLLOW»	i
Макс. количество внутренних ссылок	Показывает страницы с более чем [100] исходящими внутренними ссылками. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Макс. количество внешних ссылок	Показывает страницы с более чем [10] исходящими внешними ссылками. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Перенаправления
Редирект, заблокированный в robots.txt	Показывает адреса страниц, возвращающие перенаправление на URL, который заблокирован в файле robots.txt. В отчёте будут отображены все URL из цепочки редиректов, которые ведут на заблокированный адрес	x
Битый редирект	Показывает адреса страниц, возвращающие перенаправление на недоступные URL (разрыв соединения с сервером, превышение времени ожидания ответа и т. п.) или URL, которые возвращают код ответа сервера 4хх и 5хх	x
Бесконечный редирект	Показывает адреса страниц, которые перенаправляют в итоге сами на себя, образуя тем самым бесконечный редирект	x
Макс. количество редиректов	Показывает адреса страниц с более чем [3] редиректами. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «Основные»)	x
Цепочка редиректов	Показывает URL с цепочками перенаправлений (более 1 редиректа)	~
Редирект на внешний сайт	Показывает внутренние URL, возвращающие 3хх редирект на внешний ресурс, который не является частью анализируемого сайта	~
301 редирект: Moved Permanently	Показывает внутренние URL, возвращающие 301 редирект	~
302 редирект: Moved Temporarily	Показывает внутренние URL, возвращающие 302 редирект	~
Редирект с мета-тегом Refresh	Показывает адреса страниц, которые содержат директиву REFRESH в HTTP-заголовках ответа сервера или тег <meta http-equiv=»refresh» /> в блоке HEAD, указывающие на другой URL	~
Canonical, заблокированный в robots. txt	Содержимое директивы CANONICAL в HTTP-заголовках ответа сервера или тега <link rel=»canonical» /> в блоке HEAD	x
Цепочка Canonical	Показывает URL с цепочками CANONICAL (канонические страницы, ссылающиеся на страницы, которые в свою очередь имеют ссылки на другие канонические страницы). При этом должно быть более 1 канонической страницы в цепочке	~
Дубликаты Canonical URL	Показывает страницы с одинаковыми каноническими URL в тегах <link rel=»canonical» /> блока HEAD или в HTTP-заголовке «Link: rel=»canonical»»	i
Неканонические страницы	Показывает неканонические страницы, у которых URL в теге <link rel=»canonical» /> или HTTP-заголовке «Link: rel=»canonical»» указывает на другую страницу	i
Страницы с версиями HTTP / HTTPS	Страницы, доступные по протоколам HTTP / HTTPS и отдающие код ответа сервера 200 (они же являются дубликатами страниц)	~
PageRank
Висячий узел	Показывает страницы, которые были определены алгоритмом расчета внутреннего PageRank как «висячие узлы». Это страницы, на которые ведут ссылки, но на них самих отсутствуют исходящие ссылки, либо они закрыты от роботов инструкциями по сканированию	x
Отсутствуют входящие ссылки	Показывает страницы, которые были определены алгоритмом расчёта внутреннего PageRank как недостижимые. Это страницы, на которые алгоритмом не было найдено ни одной входящей ссылки (это может возникать при сканировании списка URL, которые никак не связаны между собой)	i
Отсутствуют исходящие ссылки	Показывает адреса страниц, у которых после применения алгоритма расчёта внутреннего PageRank не были найдены исходящие ссылки (это зачастую происходит, когда исходящие со страницы ссылки ещё не были просканированы)	i
Перенаправление	Показывает URL, которые были определены алгоритмом расчета внутреннего PageRank как перенаправляющие ссылочный вес (это могут быть адреса страниц, возвращающих 3хх редирект или содержащих инструкции canonical / refresh, которые указывают на другой URL)	~
Индексирование и сканирование
4xx ошибки: Client Error	Показывает URL, которые возвращают 4xx код ответа сервера	x
5xx ошибки: Server Error	Показывает URL, которые возвращают 5xx код ответа сервера	x
Неправильный формат тега Base	Показывает страницы, содержащие тег BASE с неправильным форматом	x
Заблокировано в robots. txt	Показывает URL, запрещенные к сканированию с помощью инструкции Disallow в файле robots.txt	~
Заблокировано в Meta Robots	Показывает страницы, запрещенные к индексации с помощью инструкции <content=»noindex»> в тегах <meta name=»robots» /> блока HEAD	~
Заблокировано в X-Robots-Tag	Показывает URL, запрещенные к индексации с помощью директивы NOINDEX поля X-Robots-Tag в HTTP-заголовках ответа сервера	~
Nofollow в Meta Robots	Показывает HTML-страницы, содержащие директиву NOFOLLOW в тегах <meta name=»robots» /> блока HEAD	i
Nofollow в X-Robots-Tag	Показывает HTML-страницы, содержащие директиву NOFOLLOW в поле X-Robots-Tag HTTP-заголовков ответа сервера	i
Отсутствующий или пустой файл robots. txt	Показывает страницы, в хосте которых файл robots.txt отсутствует или пустой	i
Онпейдж
Дубликаты страниц	Показывает полные дубли страниц по всему HTML-коду страницы	x
Дубликаты текста	Показывает дубликаты страниц по текстовому содержимому блока без учета HTML-кода (plain-html)	x
Отсутствующий или пустой Title	Показывает страницы с отсутствующим или пустым тегом TITLE	x
Отсутствующий или пустой Description	Показывает страницы с отсутствующим или пустым тегом DESCRIPTION	x
Отсутствующий или пустой h2	Показывает страницы с отсутствующим или пустым тегом h2	x
Дубликаты Title	Показывает страницы с дублирующимися тегами TITLE	~
Дубликаты Description	Показывает страницы с дублирующимися тегами DESCRIPTION	~
Дубликаты h2-H6	Показывает страницы с дублирующимися заголовками h2	~
Несколько тегов Title	Показывает страницы, которые содержат более одного тега TITLE	~
Несколько тегов Description	Показывает страницы, которые содержат более одного тега DESCRIPTION	~
Несколько заголовков h2	Показывает страницы, которые содержат более одного тега h2	~
Одинаковые Title и h2-H6	Показывает страницы, у которых заголовок h2-H6 совпадает с содержимым тега TITLE	~
Мин. размер контента	Показывает страницы с менее чем [2000] символов в блоке <body> (без HTML-тегов). Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	~
Кодированные URL	Показывает URL, которые содержат кодированные (не ASCII) символы и пробелы. Например, URL вида https://example.com/при кодируется как https://example.com/%D0%BF%D1%80%D0%B8	i
Макс. длина Title	Показывает страницы, у которых длина тега TITLE более [70] символов. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Макс. длина Description	Показывает страницы, у которых длина тега DESCRIPTION более [250] символов. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Макс. длина h2-H6	Показывает страницы, у которых длина тегов h2-H6 более [60] символов. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Короткий Title	Показывает страницы, у которых длина тега TITLE менее [5] символов. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Короткий Description	Показывает страницы, у которых длина тега DESCRIPTION менее [70] символов. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Короткий h2-H6	Показывает страницы, у которых длина тегов h2-H6 менее [5] символов. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Макс. размер HTML	Показывает страницы с более чем [50] тыс. символов в блоке <html> (включая HTML-теги). Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Макс. размер контента	Показывает страницы с более чем [50] тыс. символов в блоке <body> (без HTML-тегов). Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Мин. соотношение Text/HTML	Показывает страницы, у которых соотношение чистого текста к коду страницы менее [10%]. Данный параметр является настраиваемым и его можно поменять в настройках программы (вкладка «SEO»)	i
Локализация
Страницы с языковыми версиями	В данном разделе представлен список всех значений элементов HREFLANG, которые были найдены на страницах проекта	i
Страницы с элементами hreflang	В данном разделе представлен список всех значений элементов HREFLANG, которые были найдены на страницах проекта и значения HREFLANG не равно X-DEFAULT	i
Некорректные hreflang URLs	В данном разделе указаны все страницы, у которых ссылки в элементах hreflang ведут на страницы 404	i

Анализ сайта на ошибки: онлайн программа Netpeak Spider

Привет, друзья! В 2017 году я делала обзор программы Netpeak Spider, который позволяет проводить аудит сайтов на ошибки. Если у вас есть желание сделать комплексную проверку сайта, в этом вам поможет Netpeak Spider. Этим сервисом могут пользоваться интернет-маркетологи, специалисты по SEO, специалисты по настройке контекстной рекламы, вебмастера и т.д.

Уникальность данного инструмента в том, что он позволяет делать анализы больших сайтов, имеет гиперскорость сканирования и понятную SEO-аналитику, в результатах которой разберется даже новичок.

Разработчики этого проекта не стоят на месте, и уже в этом году они презентовали крутое обновление Netpeak Spider 3.1., в которое вошло более 300 изменений. О том, что новенького появилось в программе, и пойдет речь в моей статье.

1. Содержание:

   Высокая скорость сканирования сайтов

Я не могла не обратить внимания на скорость анализа своего сайта. Для того, чтобы просканировать мой блог, Netpeak Spider понадобилось около 10 секунд! Да, мой сайт на данный момент включает в себя всего 2 856  страниц (из аналитики Netpeak Spider), тем не менее, я видела, насколько быстро прошла обработка.

Именно на этом моменте акцентируют свое внимание специалисты данного сервиса. Они добились того, что время на анализ сайта до 10 000 страниц сократилось в 8 раз, а для сайтов более 100 000 страниц практически в 30 раз.

Также они смогли снизить потребление оперативной памяти до 235 Мб и потребление памяти на жестком диске до 30 Мб.

Кстати, теперь при анализе сайта происходит мониторинг лимита памяти для сохранения данных. Если памяти не хватает, программа останавливает свою работу и выдает соответствующее сообщение. В этом случае вы можете сохранить проект, выгрузить его, а затем продолжить далее.

Остановить работу программы вы можете и самостоятельно, т.е. возможно частичное сканирование сайта с сохранением результата. Следующее сканирование возобновится с этого момента.

2. Обновление таблицы после исправления ошибок и удаление URL

В обновленной версии Netpeak Spider теперь появилась возможность пересканировать таблицу с URL, которые содержат ту или иную ошибку.

Пример. Сервис показал, что на вашем сайте присутствуют битые ссылки, как у меня.

Если кликнуть по этому параметру, в левой части окна программы вы увидите URL, где спряталась эта битая ссылка. Удалив ее с сайта, вам не нужно пересканировать весь блог снова. Достаточно в программе выделить эту ссылку правой кнопкой мыши, выбрать команду Текущая таблица – Пересканировать таблицу.

Если в списке ошибок вы нашли URL и знаете, что на этих страницах сайта все правильно, эти URL из таблицы можно удалить. Для этого по адресу страницы кликните правой кнопкой мыши и выберите функцию Удалить URL.

3. Новая вкладка Параметры

Обратите внимание, что из настроек Netpeak Spider параметры переместились в правую часть рабочего окна программы. Именно здесь вы можете выбрать те параметры, по которым хотите проанализировать свой сайт на ошибки.

Любой параметр можно добавить и во время сканирования сайта. Для этого необходимо сканирование остановить и поставить галочку у нужного параметра. Конечно, та часть сайта, которая уже просканировалась, останется без этого показателя. Но далее после возобновления сканирования этот параметр будет учтен. Также работает и обратный вариант: любую галочку из параметров можно удалить.

Клик по любому параметру выбирает в таблице ошибок столбец с этим параметром. В данном случае не нужно двигать ползунком влево-вправо, чтобы найти этот самый показатель.

В последнем обновлении появилась возможность синхронизации таблицы с параметрами. Если вы хотите выгрузить таблицу с определенными параметрами, а остальные отключить, для этого просто снимите галочки с параметров в правой панели сервиса.

4. Сегментация и дашборд

Дашборд – это новая функция, которая позволяет анализировать показатели сканирования сайта в виде диаграмм.

Здесь вы можете ознакомиться со следующими показателями:

• Количество просканированных URL
• URL с важными ошибками
• Индексируемые URL
• Внутренние URL
• Индексируемость URL
• Критичность ошибок
• Причины неиндексируемости URL
• Время ответа сервера
• Код ответа сервера
• Глубина URL
• Инструкции по индексации
• Тип контента

Если вы обратите внимание на 1-й показатель Индексируемость URL по моему сайту, то нельзя не заметить, что индексируется у меня всего 10% информации. Не стоит пугаться, т.к. остальная часть – это скриншоты (картинки) – не HTML.

Это, кстати, видно по нижнему графику, который отвечает за тип контента.

Очень удобно, что каждый сегмент графика кликабельный.

Например, меня заинтересовал сегмент графика с высокой критичностью ошибок.

Чтобы посмотреть список ошибок, мне достаточно кликнуть мышкой по этому сегменту. И передо мной откроется таблица со списком этих ошибок.

Но это еще не все! Теперь у вас появилась возможность самостоятельно любую ошибку представить в виде сегмента. Допустим, в программе вас заинтересовал раздел ошибок со средней критичностью. Для этого вы должны выделить эту ошибку и кликнуть по кнопке Применить как сегмент.

В результате появится дашборд с соответствующими диаграммами, через которые легче определить источники ошибок.

5. Удобная выгрузка отчетов

Все результаты сканирования сайта можно выгрузить и сохранить в таблице excel или CSV. Для этого в программе необходимо кликнуть по кнопке Экспорт и выбрать тот раздел, в формате которого вы хотите увидеть результаты.

Это может быть набор основных отчетов, все ошибки, отчеты по ошибкам, в том числе битые ссылки, ссылки с неправильным форматом  URL, изображения без атрибута ALT, редиректы; массивные отчеты из базы данных, в том числе все внутренние и внешние ссылки, уникальные URL и анкоры; отчет  по структуре сайта, и т.д.

6. Дополнительные инструменты

О дополнительных инструментах Netpeak Spider я уже упоминала в первой статье, но не будет лишним еще раз повторить. Для анализа своего сайта вы можете воспользоваться дополнительными инструментами:

• Расчет внутреннего PageRank
• Валидатор XML Sitemap
• Генератор Sitemap

Расчет внутреннего PageRank определяет висячий узел. Висячие узлы – это URL, которые получают ссылочный вес, но не передают его дальше. Проще говоря, это страница, на которую идут входящие ссылки, а исходящих ссылок нет.

С помощью Netpeak Spider нас воем блоге я обнаружила такую ошибку. Дело в том, что я удалила некоторые рубрики с сайта, а статьи раскидала по другим рубрикам. Но как оказалось, в одной из моих статей была ссылка на удаленную рубрику. В  результате образовался висячий узел, от которого необходимо избавиться. Netpeak Spider считает эту ошибку критичной.

Если на вашем блоге карта сайта Sitemap не генерируется автоматически, ее можно сгенерировать с помощью инструмента Netpeak Spider — Генератор Sitemap. В результате данная карта будет отвечать рекомендациям Google и  Яндекс, и будет соответствовать протоколу Sitemap.

7. Сохранение шаблонов настроек

Наверное, с этого обновления и нужно было начинать, т.к. работа со всеми программами начинается с настроек.

Теперь Netpeak Spider позволяет сохранять шаблоны настроек. Для этого в настройках вам нужно лишь кликнуть по кнопке Сохранить и ввести название ваших настроек. При следующем запуске анализа сайта нет необходимости снова выставлять нужные настройки – просто выберите сохраненный вариант.

8. Виртуальный robots.txt

Так же в настройках можно настроить виртуальный robots.txt или протестировать любую директиву  из «роботса» перед заливкой на сайт.

9. Анализ списка URL

Если вдруг у вас возникла необходимость проанализировать на ошибки не весь сайт, а только некоторые страницы, вы можете это сделать, добавив списком URL (из файла) через кнопку Экспорт в программе.

10. Быстрый поиск по таблице

Теперь, чтобы найти определенный URL, можно воспользоваться новой функцией Быстрый поиск по таблице. Просто вставьте интересующий вас адрес в поле поиска, и система выдаст вам готовый результат.

11. Удобный фильтр

Ну и в заключение хочу познакомить вас с удобным фильтром, который позволяет найти группу ошибок в один клик. Для этого в таблице правой кнопкой мыши кликните по ошибке и выберите функцию Фильтровать по значению. Система отберет все страницы, где встречается эта ошибка.

Заключение

Как видите, с Netpeak Spider проводить анализ сайта на ошибки стало еще проще, при минимальных затратах времени и ресурсов вашего компьютера. Интуитивный функционал, всплывающие подсказки, выгрузка отчетов в виде таблиц позволит работать с этой программой любому новичку. Ну а продвинутые пользователи найдут для себя здесь современные решения для работы над задачами разной сложности.

Автор статьи Ольга Абрамова

Денежные ручейки

Обработка висячих узлов — PageRank | Арпан Сардар

Это продолжение моей предыдущей статьи. Я бы порекомендовал своим читателям сначала прочитать эту статью. Здесь я расскажу о висячих узлах и о том, как их можно обработать в алгоритме PageRank.

В области сетевого анализа висячих узлов — это узлы, не имеющие внешних ребер . На приведенном ниже рисунке узел « B » является висячим узлом, поскольку у него нет исходящих ссылок. Мы все знаем, что большинство веб-страниц ссылаются на другие страницы и на них ссылаются другие страницы, но есть также много страниц без каких-либо исходящих ссылок 9.0005 Рисунок: Простая направленная сеть

в сети WWW. С каждой итерацией обновления значений PageRank эти пресловутые узлы продолжают поглощать PageRank других узлов все больше и больше и в конечном итоге приводят к тому, что узлы получают значение PageRank 0 или 1 во время схождения . Объяснение состоит в том, что случайный серфер в Интернете, имея достаточное количество времени , всегда в конечном итоге достигнет висячего узла и остановить просмотр через веб-страниц через гиперссылки. Рассмотрим это явление на простом примере. Сначала создадим направленную сеть с висячим узлом, а затем визуализируем ее через график.

Код для создания и визуализации направленной сети

Сеть показана ниже. Он состоит из одного оборванного узла « C ».

Рисунок: Направленная сеть с висячим узлом «C»0003 введите в код, который я обсуждал в предыдущей статье.

Результат нашей собственной реализации PageRank

Мы видим, что узлы получили PageRank ровно 0 или 1 . Это аномалия , о которой я упоминал ранее. Здесь узел «C» — это , поглощающий значения PageRank других узлов в сети, поскольку мы не обрабатывали ситуацию с приемниками (страницы без исходящих ссылок) в нашем коде. Давайте далее проанализируем, как значения узлов обновляются с каждой итерацией, пока они не сойдутся.

Значения PageRank узлов для каждой итерации

Порядок убывания узлов с точки зрения их PageRank равен C, A, B, D, E , который получен из нашего кода. Давайте посмотрим, как должен выглядеть правильный порядок , применив встроенную функцию PageRank networkx .

Применение встроенной в networkx функции PageRankВывод встроенной функции

Итак, наш код не дает правильного результата для сети с оборванными узлами. Теперь давайте рассмотрим раковины с концепцией 9.0003 коэффициент демпфирования. Коэффициент демпфирования d обозначает вероятность того, что воображаемый пользователь продолжит просматривать веб-страницы, щелкнув случайную гиперссылку из любого узла. Значение d равно , обычно устанавливается равным 0,85 и . Я буду учитывать то же самое в своем коде. Выделенная ниже часть — единственная модификация, которой не хватало в коде, рассмотренном в предыдущей статье. Здесь на каждой итерации все узлы сохраняют 85% их обновленных PageRank и сумма остальных 15% значений PageRank всех узлов поровну делится между ними. В каждой итерации общее значение PR для n узлов всегда равно 1 . Таким образом, присвоение 15% всем узлам означает, что каждый узел получает общее значение (0,15 / n) , которое добавляется к 85% из их значений PR , которые сохранил каждый узел. Таким образом, , используя концепцию коэффициента демпфирования, мы можем предотвратить сходимость узлов со значением 0 или 1.

Модифицированная функция (полный код см. по ссылке GitHub ниже)

Теперь наш модифицированный код дает следующий вывод. Обратите внимание, что это то же самое, что и вывод встроенной в networkx функции PageRank. Итак, делаем вывод, что измененный код правильно выдает вывод, предотвращающий стоки.

Вывод модифицированного кода

На следующем рисунке подробно показана каждая итерация до сходимости.

Значения PageRank узлов для каждой итерации модифицированного кода

Итак, это был мой подход к работе с приемниками на наличие висячих узлов в сети. Обратите внимание, что окончательные значения PageRank узлов могут немного отличаться от значений встроенной в networkx функции PageRank. Это связано с тем, что у networkx может быть более надежный подход к решению этой проблемы, или они могли рассмотреть другое значение сходимости и т. д.

• Полный код можно найти здесь. Модификации приветствуются. 🙂
• Свяжитесь со мной в LinkedIn, если у вас есть какие-либо вопросы или предложения.

Для этой реализации я использовал Метод распределения баллов . В моей следующей статье я реализовал алгоритм, используя метод случайного блуждания .

Спасибо!

Алгоритм PageRank, полное объяснение | by Amrani Amine

Алгоритм PageRank или алгоритм Google был представлен Лари Пейдж, одним из основателей Google. Впервые он был использован для ранжирования веб-страниц в поисковой системе Google. В настоящее время он все больше и больше используется во многих различных областях, например, для ранжирования пользователей в социальных сетях и т. д. Что интересно в алгоритме PageRank, так это то, как начать со сложной проблемы и в конечном итоге найти очень простое решение. В этом посте я расскажу вам об идее и теории алгоритма PageRank. Вам просто нужно иметь некоторые основы в алгебре и цепях Маркова. Здесь мы будем использовать ранжирование веб-страниц в качестве примера использования для иллюстрации алгоритма PageRank.

взято мной

Случайное блуждание

Сеть может быть представлена ​​в виде ориентированного графа, где узлы представляют веб-страницы, а ребра образуют связи между ними. Как правило, если узел (веб-страница) i связан с узлом j , это означает, что i относится к j .

Пример ориентированного графа

Нам нужно определить важность веб-страницы. В качестве первого подхода мы могли бы сказать, что это общее количество веб-страниц, которые ссылаются на него. Если мы остановимся на этом критерии, важность этих веб-страниц, которые ссылаются на него, не будет принята во внимание. Другими словами, важная веб-страница и менее важная имеют одинаковый вес. Другой подход состоит в том, чтобы предположить, что веб-страница распределяет свою важность в равной степени на все веб-страницы, на которые она ссылается. Сделав это, мы можем затем определить счет Узел J Следующий:

, где Rᵢ -это оценка узла I и . и . 1 1 1 1 1 1 1 1 1 1 141 .

Из приведенного выше примера мы можем написать эту линейную систему:

Передавая правую часть этой линейной системы в левую часть, мы получаем новую линейную систему, которую мы можем решить с помощью исключения Гаусса. Но это решение ограничено для небольших графов. Действительно, поскольку графы такого типа разрежены, а исключение Гаусса изменяет матрицу при выполнении своих операций, мы теряем разреженность матрицы, и она требует больше памяти. В худшем случае матрица больше не может быть сохранена.

Цепь Маркова и PageRank

Поскольку цепь Маркова определяется начальным распределением и матрицей перехода, приведенный выше график можно рассматривать как цепь Маркова со следующей матрицей перехода:

Матрица перехода, соответствующая нашему примеру

Заметим, что P транспонирование является стохастическим по строкам, что является условием применения теорем о цепях Маркова.
Для начального распределения будем считать, что оно равно:

, где n — общее количество узлов. Это означает, что случайный ходок случайным образом выберет начальный узел, из которого он может добраться до всех других узлов.

На каждом шаге случайный ходок будет переходить к другому узлу в соответствии с матрицей перехода. затем вычисляется распределение вероятностей для каждого шага. Это распределение говорит нам, где вероятно будет случайный ходок после определенного количества шагов. Распределение вероятностей вычисляется с использованием следующего уравнения:

Стационарное распределение цепи Маркова — это распределение вероятностей π с π = Pπ . Это означает, что распределение не изменится после одного шага. Важно отметить, что не все цепи Маркова допускают стационарное распределение.

Если цепь Маркова сильно связна, что означает, что любой узел может быть достигнут из любого другого узла, то она допускает стационарное распределение. В нашей проблеме так. Итак, после бесконечно долгого блуждания мы знаем, что распределение вероятностей будет сходиться к стационарному распределению π .

Все, что нам нужно сделать, это решить это уравнение:

Заметим, что π является собственным вектором матрицы P с собственным значением 1 90. Вместо того, чтобы вычислять все собственные векторы P и выбирать тот, который соответствует собственному значению 1 , мы используем теорему Фробениуса-Перрона .

По Фробениуса-Перрона , если матрица A является квадратной и положительной матрицей (все ее элементы положительны), то она имеет положительное собственное значение r , например |λ| < r , где λ является собственным значением A . Собственный вектор v A с собственным значением r является положительным и единственным положительным собственным вектором.

В нашем случае матрица P положительная и квадратная. Стационарное распределение π обязательно положительно, потому что это распределение вероятностей. Мы заключаем, что π является доминирующим собственным вектором P с доминирующим собственным значением 1 .

Чтобы вычислить π , мы используем итерацию степенного метода, которая является итеративным методом для вычисления доминирующего собственного вектора данной матрицы А . Из начального приближения доминирующего собственного вектора b , который может быть инициализирован случайным образом, алгоритм будет обновлять его до сходимости, используя следующий алгоритм: определяет вероятность того, что пешеход окажется в узле после t шагов. Это означает, что чем выше вероятность, тем важнее узел. Затем мы можем ранжировать наши веб-страницы в соответствии со стационарным распределением, которое мы получаем, используя метод мощности.

Коэффициент телепортации и демпфирования

Например, в веб-графике мы можем найти веб-страницу i , которая ссылается только на веб-страницу j и j 0 ссылается только на 30 i 0 . Это то, что мы называем проблемой ловушки для пауков . Мы также можем найти веб-страницу, на которой нет исходящей ссылки. Его обычно называют Тупик .

Тупики и ловушки для пауков, иллюстрация

В случае ловушки для пауков, когда случайный ходок достигает узла 1 в приведенном выше примере, он может перейти только к узлу 2 , а с узла 2 он может добраться только узел 1 и так далее. Важность всех остальных узлов будет приниматься узлами 1 и 2 . В приведенном выше примере распределение вероятностей будет сходиться к π = (0, 0,5, 0,5, 0) . Это не желаемый результат.

В случае тупиков, когда ходок достигает узла 2 , он не может достичь другого узла, потому что у него нет исходящего канала. Алгоритм не может сходиться.

Чтобы преодолеть эти две проблемы, мы вводим понятие телепортации .

Телепортация заключается в соединении каждого узла графа со всеми остальными узлами. После этого график будет завершен. Идея с определенной вероятностью β , случайный блуждающий перейдет к другому узлу в соответствии с матрицей перехода P и с вероятностью (1-β)/n , он перейдет случайным образом к любому узлу в графе . We get then the new transition matrix R :

where v is a vector of ones, and e a vector of 1/n

β обычно определяется как коэффициент демпфирования . На практике рекомендуется установить β на 0,85 .

Применяя телепортацию в нашем примере, мы получаем следующую новую матрицу перехода:

Наша новая матрица перехода

Матрица R имеет те же свойства, что и P , что означает, что она допускает стационарное распределение, поэтому мы можем использовать все теоремы, которые видели ранее.

Вот и все для алгоритма PageRank. Надеюсь, вы поняли интуицию и теорию алгоритма PageRank. Пожалуйста, не стесняйтесь оставлять комментарии или делиться моей работой.

Спасибо!

«Коды::Позиционирование»

«Коды::Позиционирование»

Подробности для темы ID=262, Codes::Postioning

• Общие словосочетания с использованием упрощенного распознавания словосочетаний. и специальная оценка
• Наиболее типичные слова, упорядоченные по частям речи, затем вероятность
• Случайные слова, сгенерированные выше, но последние 50 плохие (?)
• Наиболее типичные документы, оценка – это примерное количество слов-компонентов в документе
• Документы с высоким рейтингом, оценка — это вероятность посещения по тематическому PageRank

Общие фразы:

сторона; левая сторона; правая сторона; Обратная сторона; бок о бок; Правая рука; сторона руки; Южная сторона; бок о бок; сверху вниз;

Наиболее типичные слова:

Наиболее типичная форма	Вероятность		Наиболее типичная форма	Вероятность		Наиболее типичная форма	Вероятность
NOUNS
hand	0. 012655		feet	0.01264		side	0.012456
head	0.0089377		leg	0.0074363		position	0.0069328
body	0.0066117		front	0.0063778		top	0.0063332
end	0.0057267		arms	0.0053541		finger	0.0050568
ground	0.0048328		line	0,004817		сзади	0,0043829
справа	0,0042272 94473	0471 bottom	0.0039012		step	0.0038001
rope	0.0037397		ball	0. 003488		move	0.0032838
direction	0.003262		движение	0,0032422		стена	0,0027427
путь	0472	0.0025881		turn	0.0025455		shoulder	0.0025177
hole	0.0024394		opponent	0.0024385		door	0.0023998
пол	0,0022948		столб	0,002273		палка	0,0022382	0471
motion	0.0021788		Middle	0.002046		techniques	0.0020282
Hook	0.0020173		weight	0. 0019667		type	0,0018805
место	0,0018795		петля	0,0018607	2

10472 objects 0.0018379 point 0.0017824 edge 0.0017754 length 0.0017527 VERBS held 0.0060637 перемещено 0,0056693 сделано 0,0045018 Звонил 0,0041857 left 0.0038695 See 0.0038091 pulled 0.0037922 thrown 0.0036475 turned 0.0034047 performed 0,0032244 размещенный 0,003037 лицо 0,0029885 allowed 0. 0029607 pushed 0.0029538 will 0.0027556 ​​ jump 0.0026793 may 0.0026743 run 0.0026704 до 0,0026 прикрепленный 0,0025594 стойки 0,047713 hit 0.0024573 caught 0.0021758 bent 0.002158 walk 0.0021491 ADJECTIVES left 0,0064185 правый 0,0056504 длинный 0,0032582 short 0.0024563 small 0.0022948 same 0. 0019182 similar 0.0018557 double 0.0017626 open 0.0017487 нижний 0,001718 верхний 0,0015208 вертикальный 0,04710472 large 0.0014325 ADVERBS up 0.01042 when 0.010188 down 0.0092142 back 0.0078882 then 0.0075403 out 0.0066097 while 0.0053997 off 0.0049527 so 0.004374 usually 0. 0042312 where 0.0040043 forward 0.0039924 URL-адреса википедия/веревка 0,00014618 википедия/рука 0,000112480471 википедия/узел 9.1671e-05 http://category/Promotion_and_marketing_communications 8.5725e-05

Случайных слов:

кал, катушка, флаер, композитор, глаз, край, мяч, уксус, взгляд, часть, святой георгий, рука, нога, движение, тяжелая утрата, подвешивание, ребенок, шок, сальто, ловушка, лицо, фронт, середина, орфография, маневр, побег, рука, танцор, вид, лицо, столб, плечо, середина, нос, направление, площадь, фастбол, ноздря, палец, путь, плавник, линия, голова, половина, право, путь, коллега, Элис, конец, ответчик, глаз, линька, положение, длина, ступня, вариация, земля, петля, доска, падение, угол, человек, ступня, сила, травма, вершина, тело, шаг, движение, широкая, тело, бросок, центр, спина, удар, ngyã, указательный, подветренный, дверь, часть, порция, палец, верх, шаг, сторона, угол, хлыст, юбка, рука, пронзающий, верх, ножка, середина, стол, сила, элемент, волна, спина, скорость, задняя часть, последовательность, спуск, рука, указатель, пользователь, круг, кран, нога, живот, направление, нога, мартинет, вариация, часть, сторона, рука, линия, крюк, крюк, тележка, перед, нос, веревка, колено, панель, контакт, маклерство, высота, подбородок, грудь, право, шея, двор, штрих, вращение, рука, июнь, ноя, аддит ion, et, уильям, суд, дань, википедия, навальный, майкл, клуб, мэттью, фут, отец, æ, парк, 6, обзор, март, база данных, команда, вот, isbn, каролина, америка, инжиниринг, аэропорт, персонаж, битва, америка, 1, поэт, округ, май, джордж, победитель, клуб, награда, человек, журнал, движение, город, население, джунгли, железная дорога, дом, газета, гора, глава, структура, животное, район, å, поколение, граница, тета, майкл, 9, правильно, История, Расширение, Команда, Совет, Личность, клавиатура, Колледж, Граница, Октябрь, Население, род, Награждать, прозвище, Грузия, Движение, 9, деревня, Отдел, Игрок, стена, друг, Университет, 24, Дэвид , брат, чемпионат, сотня, музыка, википедия, е, деревня, 3, 3, проблема, чемпионат, полоса, день, среда, праздник, скан, домашнее хозяйство, гарри, в, моцарт, экономический, курс, паутина, индивидуальный, с , друг, Орел, пик, å, Станция, Отдел, Образование, ссылка, год, список, 1, город, ã, группа, Война, Университет, Население, ссылка, возраст, Система, округ, Март, Война, год, Мир , 65, 3, население, ñ, поддержка, человек, ссылка, искусство, город, запад, университет, 3, мир, поддержка, война, семья, значения, время, город, нормандия, доминатор, многоточие, дропкик, выживший, лань , одеон, коннор, все-ирландия, вольфрам, люфтганза

Наиболее типичные документы:

List_of_professional_wrestling_throws(3689,4) Professional_wrestling_holds(3251) Скейтбординг_трюк(2423. 2) List_of_breakdance_moves(2274.2) Воздушное_(танцевальное_движение)(2070.7) Разворот (2023.8) Equine_conformation (1905.2) Professional_wrestling_attacks(1754.8) Суплекс (1600,4) Professional_wrestling_double-team_maneuvers(1338.9) Профессиональная_борьба_воздушные_техники (1248.1) Глоссарий_из_фехтования_терминов(1114) List_of_cricket_terms (1000,7) Frisbee_throws(961.03) Жест (943.2) Глоссарий_терминов_альпинизма (879.2) Takeshi’s_Castle_Challenges(867,76) Johnston-Ruyer_Back_Therapy(865.21) List_of_school_pranks(844,19) Несчастный_подъем (841,66) Глоссарий_of_partner_dance_terms(838.25) Глоссарий_американского_футбола(823.67) Волейбол(823,2) Быстрый_боулинг(820,77) Лестница(804.44) List_of_sex_positions(774,59) Контрданс (763,68) Силовая бомба(751.09) Брасс (739,84) College_football_glosary(735,72)

Высокопоставленные документы:

Категория:Викимедиа(0,0011771) Категория:Узлы(0.00074346) Узел (0,00060258) Категория:Культура(0.0005527) Категория:Отдых(0.00043349) Викимедиа_Коммонс (0,00034882) Категория:Водный_транспорт(0.