«Основы электродинамики. Магнитное поле. Явление электромагнитной индукции» (11 класс)
Тест по теме «Основы электродинамики. Магнитное поле. Явление электромагнитной индукции» 11 класс
1.Магнитное поле создается…
1)неподвижными электрическими зарядами; 2)движущимися электрическими зарядами;
3)телами, обладающими массой; 4)движущимися частицами.
2.Постоянное магнитное поле можно обнаружить по действию на…
1) движущуюся заряженную частицу; 2) неподвижную заряженную частицу;
3) любое металлическое тело; 4) заряженный диэлектрик.
3. Что наблюдалось в опыте Эрстеда?
1) взаимодействие двух параллельных проводников с током. 2) поворот магнитной стрелки вблизи проводника при пропускании через него тока. 3)взаимодействие двух магнитных стрелок 4)возникновение электрического тока в катушке при вдвигании в нее магнита.
4. Как взаимодействуют два параллельных проводника при протекании в них тока в противоположных направлениях?
1)сила взаимодействия равна нулю; 2)проводники притягиваются;
3)проводники отталкиваются; 4)проводники поворачиваются.
5. Как называется единица магнитной индукции?
1)Тесла 2)Генри 3)Вебер 4)Ватт
6. Как называется сила, действующая на движущуюся заряженную частицу со стороны магнитного поля?
1) Сила Ампера; 2)Центробежная сила; 3)Сила Лоренца; 4)Центростремительная сила
7. Какова траектория протона, влетевшего в однородное магнитное поле параллельно линиям индукции магнитного поля?
1)Прямая 2)Парабола 3)Окружность 4)Винтовая линия
8. Изменится ли, а если изменится, то, как частота обращения заряженной частицы в циклотроне при увеличении ее скорости в 2 раза. Скорость частицы считать намного меньше скорости света
1)Увеличится в 2 раза 2)Увеличится в 4 раза 3)Увеличится в 16 раз. 4)Не изменится
9. Электрон и протон влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями. Отношение модулей сил, действующих на них в этот момент времени со стороны магнитного поля, равно
1) 1 2) 0 3) 1/2000 4) 2000
10. Участок проводника длиной 10 см находится в однородном магнитном поле с индукцией 50 мТл. Сила тока, протекающего по проводнику, 10 А. Какую работу совершает сила Ампера при перемещении проводника на 8 см в направлении действия силы. Проводник расположен перпендикулярно линиям магнитного поля
1) 0,004 Дж. 2) 0,4 Дж. 3) 0,5 Дж. 4) 0,625 Дж
11.Рамку площадью 0,5 м2 пронизывают линии магнитной индукции магнитного поля с индукцией 4 Тл под углом 300 к плоскости рамки. Чему равен магнитный поток, пронизывающий рамку?
1) 1 Вб 2) 2,3 Вб 3) 1,73 Вб 4) 4 Вб
12.В магнитном поле с индукцией 4 Тл движется электрон со скоростью 107 м/с, направленной перпендикулярно линиям индукции магнитного поля. Чему равен модуль силы, действующий на электрон со стороны магнитного поля?
1) 0,4 пН; 2) 6,4 пН; 3) 0,4 мкН; 4) 6,4 мкН
13.Если величину заряда увеличить в 3 раза, а скорость заряда уменьшить в 3 раза, то сила, действующая на заряд в магнитном поле,
1) не изменится; 2)увеличится в 9 раз; 3)уменьшится в 3раза; 4) увеличится в 3 раза.
14. Заряд движется в магнитном поле. Индукция магнитного поля и скорость заряда увеличиваются в 3 раза. Сила, действующая на заряд
1) увеличится в 3 раза; 2) уменьшится в 3раза;
3) увеличится в 9 раз; 4) уменьшится в 9 раз.
15. Определить индукцию магнитного поля проводника, по которому протекает ток 4 А, если поле действует с силой 0,4 Н на каждые 10 см проводника.
1) 0,5 Тл; 2) 2Тл; 3) 1 Тл; 4) 0,1 Тл.
16. Линии магнитного поля в пространстве вне постоянного магнита
1) начинаются на северном полюсе магнита, заканчиваются на южном;
2) начинаются на южном полюсе магнита, заканчиваются на бесконечности;
3) начинаются на северном полюсе магнита, заканчиваются на бесконечности;
4) начинаются на южном полюсе магнита, заканчиваются на северном.
17. С помощью правила Буравчика можно определить
1) направление силы магнитного поля; 2) направление движения заряженной частицы;
3) направление линий магнитного поля; 4)направление силы электрического поля.
18. Линии однородного магнитного поля
1) искривлены, их густота меняется от точки к точке; 2) параллельны друг другу и расположены с одинаковой густотой;
3) расположены параллельно с разной густотой; 4) расположены хаотично.
19.Разноименные полюсы магнита…, а одноименные полюсы —
1) …отталкиваются, …притягиваются; 2)…притягиваются, …отталкиваются;
3)…отталкиваются; 4)…притягиваются.
20. Частица с электрическим зарядом 8·10-19 Кл движется со скоростью 220 км/ч в магнитном поле с индукцией 5 Тл, под углом 30
1) 10-15 Н 2) 2·10-14 Н 3) 2·10-12 Н 4) 1,2·10-16 Н
21. Какая физическая величина измеряется в «генри»?
1) индукция поля 2) магнитный поток 3) ЭДС индукции 4) Индуктивность.
22. Какой из перечисленных процессов объясняется явлением электромагнитной индукции
1) отклонение магнитной стрелки при прохождении по проводу электрического тока; 2) взаимодействие проводников с током;
3) появление тока в замкнутой катушке при опускании в нее постоянного магнита;
4) возникновение силы, действующей на проводник с током.
23. Определить индуктивность катушки, через которую проходит поток величиной 5 Вб при силе тока 100 мА.
1) 0,5 Гн 2) 50 Гн 3) 100 Гн 4) 0,005 Гн Д. 0,1 Гн
24. Какова энергия магнитного поля катушки индуктивностью, равной 2 Гн, при силе тока в ней, равной 200 мА?
1) 400 Дж; 2) 4·104 Дж; 3) 0,4 Дж; 4) 4·10-2 Дж
25. Какова ЭДС индукции, возбуждаемая в проводнике, помещенном в магнитном поле с индукцией 100 мТл, если оно полностью исчезает за 0,1 с?
Площадь, ограниченная контуром, равна 1 м2.
1) 100 В; 2) 10 В; 3) 1 В 4) 0,01 В
26. Чем определяется величина ЭДС индукции в контуре?
1) Магнитной индукцией в контуре; 2) Магнитным потоком через контур ;
3) Электрическим сопротивлением контура; 4) Скоростью изменения магнитного потока
27. Определить сопротивление проводника длиной 40 м, помещенного в магнитное поле, если скорость движения 10м/с. Индукция магнитного поля равна 0,01Тл, сила тока 1А.
1) 400 Ом; 2) 0,04Ом; 3) 4Ом 4) 40 Ом
1) 400В; 2) 40В; 3) 4В; 4) 0,04В
29. Определить индуктивность катушки, если при силе тока в 2А, она имеет энергию 0,2Дж.
1) 200Гн; 2) 2мГн 3) 200мГн 4) 100мГн
30. Определить сопротивление проводника длиной 20 м, помещенного в магнитное поле, если скорость движения 10м/с, индукция поля равна 0,01Тл, сила тока 2А.
1) 100 Ом; 2) 0,01Ом; 3) 0,1Ом; Г. 1 Ом;
…
§ 113. Магнитное поле движущегося заряда
Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных
182
был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой
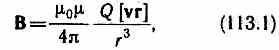
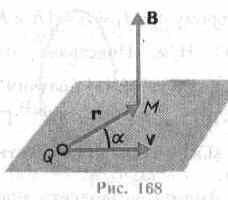
где r — радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции (113.1) вычисляется по формуле
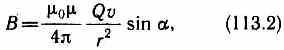
где а — угол между векторами v и r.
Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
Idl=Qv.
Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (v<<c) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени находится движущийся заряд.
Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на —Q. Скорость v — относи-
тельная скорость, т. е. скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.
Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академиком А. Ф. Иоффе, доказавшим эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.
§114. Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на проводники с током (см. §111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд
F=Q[vB], (114.1) где В — индукция магнитного поля, в котором заряд движется.
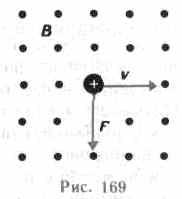
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.
183
Модуль силы Лоренца (см. (114.1)) равен
F=QvBsin,
где — угол между v и В.
Отметим еще раз (см. § 109), что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
F=QE + Q[vB].
Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
§ 113. Магнитное поле движущегося заряда
Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных
182

был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой
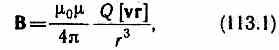
где r — радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции (113.1) вычисляется по формуле

где а — угол между векторами v и r.
Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
Idl=Qv.
Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (v<<c) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени находится движущийся заряд.
Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на —Q. Скорость v — относи-
тельная скорость, т. е. скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.
Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академиком А. Ф. Иоффе, доказавшим эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.
§114. Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на проводники с током (см. §111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой
F=Q[vB], (114.1) где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.
183

Модуль силы Лоренца (см. (114.1)) равен
F=QvBsin,
где — угол между v и В.
Отметим еще раз (см. § 109), что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
F=QE + Q[vB].
Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
Лекция 15. Магнитостатика
Магнитостатика изучает постоянные (не зависящие от времени) магнитные поля, созданные постоянными токами. Магнитное поле создается только движущимися зарядами и действует только на движущиеся заряды.
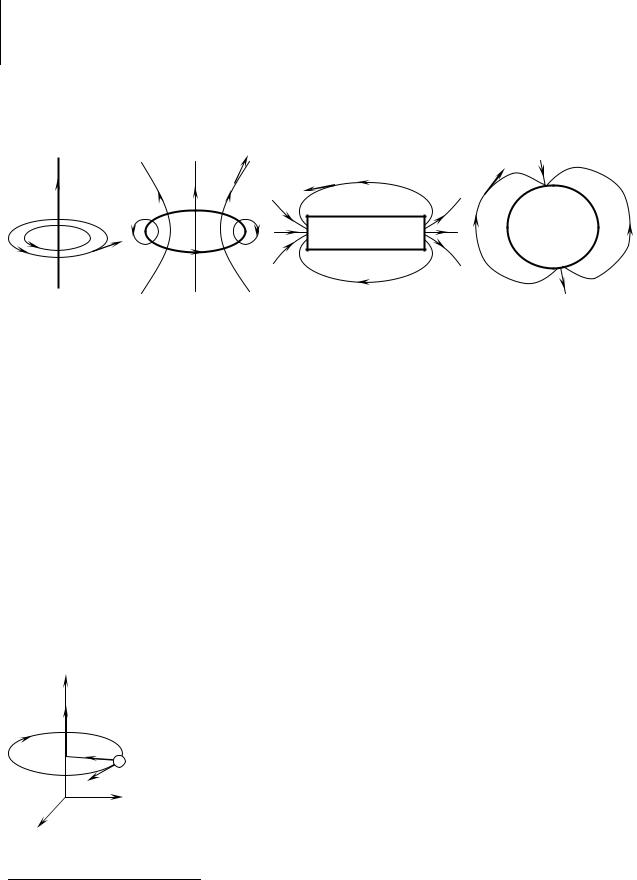
Как и электрическое, магнитное поле тоже изображается в виде силовых линий. Примеры магнитных полей различных объектов показаны на рис. 15.1: а) прямой провод; б) круговой виток; в) постоянный магнит; г) Земля1.
| Br | r |
| r | Ю.магн. |
I |
| B |
| B |
|
|
|
|
|
| |
Br |
| Ю | С |
| Земля |
I |
|
|
|
| |
|
|
|
|
| С.магн. |
а) | б) |
| в) |
| г) |
Рис. 15.1
Силовойr характеристикой магнитного поля является вектор магнитной
индукции B . Он направлен по касательной к силовой линии в какой-либо точке. Магнитнаяr стрелка ориентируется в магнитном поле по направлению векто-
ра B и показывает направление магнитного поля в пространстве.
В отличие от гравитационного и электрического полей магнитное поле
непотенциальное.
15.1. Движение зарядов в магнитном поле
В отличие от электрического поля, которое действует как на неподвижные, так и на движущиеся заряды, магнитное поле действует только на движущиеся заряды.
Еще раз подчеркнем, что силовой характеристикой магнитного поля яв-
ляется вектор магнитной индукции B : чем больше магнитное поле, тем сильнее оно действует на движущийся заряд.
r Z |
|
|
|
|
| Так, на точечный заряд q, движущийся в магнитном | |
B |
|
|
|
|
| поле со скоростью υ действует сила (сила Лоренца) |
|
|
|
|
|
| r | (15.1) | |
r |
|
|
|
|
| F = q[υ B]. | |
F |
|
|
|
| q | Эта сила меняет скорость только по направлению и не | |
| r | меняет по величине, то есть вызывает только центростреми- | |||||
| υ | тельное ускорение. Траектория движения частицы в общем | |||||
| Y | ||||||
X | случае – винтовая линия, а в случае, когда скорость перпен- | ||||||
Рис. 15.2 | дикулярна направлению вектора индукции магнитного поля |
|
1 Южный магнитный полюс Земли находится вблизи северного географического, а северный магнитный – вблизи южного географического.
98

(перпендикулярна силовым линиям магнитного поля) – окружность. Выражение для величины силы в последнем случае имеет простой вид:
причем эта сила направлена к центру окружности и вызывает центростремительное ускорение, как показано на рис. 15.2. В случае, когда скорость парал-
лельна силовым линиям, |
| F = 0, | магнитное поле на заряд не действует, и траек- | |||||||
тория заряда – прямая. |
|
|
|
|
|
|
|
|
|
|
Если движется не один заряд, а много, то есть течет постоянный ток I, то | ||||||||||
сила, действующая на протекающий заряд dq равна |
|
| ||||||||
r | r | r |
| dl | r | dq | r | r | r | r |
|
|
| B = | [dl | B]= I[dl | B], | ||||
dF = dq[υ B]= dq |
| dt | ||||||||
|
|
| dt |
|
|
|
|
| ||
где dl – бесконечно малый участок проводника, по которому прошел бесконечно малый заряд dq.
Таким образом, сила, действующая на бесконечно маленький отрезок dl
проводника с током I, помещенного в магнитное поле B , |
|
|
| ||
dF = I[dl B], |
|
| (15.2) | ||
где векторная величина Idlrназывается элементом тока, рис. 15.3. |
|
| |||
В скалярной форме это выражение имеет вид |
| B |
|
| |
dF = (IBsinα)dl, |
|
|
| ||
|
| I | |||
где α – угол между направлением магнитного поля и током. | α | ||||
Если провод прямой, а магнитное поле одинаковое вдоль |
|
|
| ||
dFr | dl | ||||
всего провода, то сила, действующая на участок провода дли- | |||||
ны l, |
| Рис. 15.3 | |||
F = I[l B], | (15.2)′ | ||||
|
|
| |||
или в скалярной форме
F = IlBsinα.
Это хорошо известный из школьного курса закон Ампера. Так как электроны ограничены проводом, они не могут двигаться по окружности, – не позволяет жесткость провода: сила Лоренца, действующая на электроны, слишком мала, чтобы свернуть провод в кольцо. Силы Лоренца и Ампера имеют одну природу (магнитные силы) и действуют на движущиеся в магнитном поле заряды. Единица измерения магнитной индукции – тесла (Тл). Из последней формулы видно, что [B] = Тл = Н/(А·м) = кг/(А·с2).
Заряженные частицы космического излучения (e, p, α,…), летящие к Земле, попадая в магнитное поле нашей планеты, движутся по винтовым траекториям вдоль силовых линий (рис. 15.1, г) к полюсам. В приполярных областях они приближаются к поверхности (где выше концентрация молекул воздуха) и возбуждают атомы азота, кислорода и других компонентов воздуха, сталкиваясь с ними. При переходе в невозбужденное состояние атомы излучают кванты света – фотоны, которые мы видим как полярное сияние.
Вообще, магнитное поле Земли совместно с атмосферой хорошо защищает живые организмы от потоков быстрых заряженных частиц, идущих от Солнца или от центра нашей галактики.
99

15.2. Магнитное поле движущихся зарядов
В отличие от электрического поля, которое создается как неподвижными, так и движущимися зарядами, магнитное поле создается только движущимися зарядами.
Из опытных фактов установлено, что величина магнитного поля в какой либо точке пространства, создаваемого точечным зарядом q, движущимся в ва-
Z |
|
|
|
|
| кууме со скоростью υ, |
|
| |||||
r | r |
| q | r | r |
| |||||||
|
|
| |||||||||||
| υ |
|
|
| |||||||||
|
|
|
|
|
| B = k1 |
|
| [υ r ], | (15.3) | |||
O | α | r3 | |||||||||||
|
|
|
|
|
|
|
| μ0 | = 10−7 Гн/м, μ0 = 1,26·10−6 |
| |||
r |
| q Y | где постоянная k1 | = | Гн/м – | ||||||||
4π | |||||||||||||
B |
|
|
|
|
|
|
|
| r – расстояние от заряда до точки | ||||
X |
|
|
|
|
| магнитная постоянная; | |||||||
Рис. 15.4 | наблюдения О. Рис. 15.4 иллюстрирует эту формулу. |
| |||||||||||
|
|
|
|
|
|
| |||||||
Согласно принципу суперпозиции магнитные поля нескольких движущихся зарядов векторно складываются, причем каждый заряд возбуждает поле независимо от наличия других зарядов.
Пусть теперь движется не один заряд, а течет постоянный ток. Рассуждая
как и в предыдущем параграфе, из формулы (15.3) получим |
| ||||||
|
|
|
| dBr = k1 | I | [dlr rr]. | (15.4) |
|
|
|
|
| |||
Z |
|
|
|
| r3 | dBr , созда- | |
|
|
| Это закон Био – Савара: магнитное поле | ||||
|
|
| |||||
| α |
| dlr | ваемое бесконечно малым элементом тока Idlr | в какой ли- | ||
O |
|
|
| бо точке зависит только от величины этого элемента и рас- | |||
r | r |
| Y | стояния r от него до этой точки (на рис. 15.5 точка наблю- | |||
dB |
| I | дения О). Как видно из формулы, с увеличением расстоя- | ||||
X |
|
|
| ния от проводника r магнитное поле уменьшается. | |||
|
|
| |||||
Рис. 15.5 |
| Этот закон используется для расчета магнитных по- | |||||
|
|
|
| ||||
лей, созданных электрическими токами различной конфигурации, например, прямым проводом, проводом в виде кольца или системы колец – катушки, поверхностными или объемными токами и т.д.
Приведем примеры магнитных полей, созданных проводниками различной формы1.
|
| Магнитное поле длинного прямого провода2 с током на | ||||||
| I | расстоянии R от него, рис. 15.6 |
| |||||
|
| B = 2k |
|
| I | . |
| (15.5) |
|
|
|
|
| ||||
| R |
| 1 R |
| ||||
| B | Сила взаимодействия двух параллельных проводов с | ||||||
| токами I1 и I2 |
| I1I2 |
|
| |||
|
| F = 2k |
| l , | (15.6) | |||
Рис. 15.6 |
| |||||||
|
| |||||||
1 |
|
| R |
| ||||
1Расчет этих полей по формуле (15.4) рекомендуется провести на дополнительном занятии.
2Длина провода много больше расстояния от него до точки наблюдения l >> R.
100
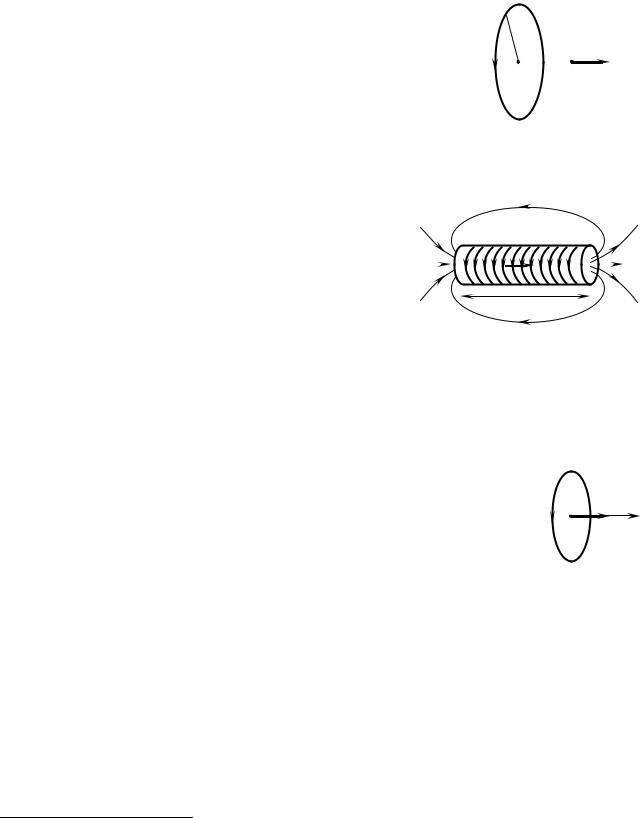
где l – длина участка провода, на который действует сила. При этом токи, текущие в одну сторону притягиваются, а в противоположные стороны – отталкиваются.
Магнитное поле кругового витка с током радиуса R на оси на расстоянии r0 от его центра, рис. 15.7
| IR2 |
|
|
|
| I |
|
| R | |||||||||||
B = 2πk1 (R2 + r | 2 )3/ 2 , | (15.7) |
|
|
|
|
| B |
|
| ||||||||||
|
|
|
|
|
| |||||||||||||||
0 |
|
|
|
|
|
|
|
|
| r0 | ||||||||||
причем выражение для поля в центре витка с током |
|
|
|
|
|
|
|
|
|
|
| |||||||||
(r0 = 0) существенно упрощается: |
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
B = 2πk1 | I |
| . |
|
| (15.7)′ |
|
|
| Рис. 15.7 | ||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Магнитное поле внутри длинной катушки1 с током (соленоида) длины l с | ||||||||||||||||||||
числом витков N, рис. 15.8 | IN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
B = 4πk |
| . | (15.8) |
|
|
|
|
|
| I | ||||||||||
|
|
|
| |||||||||||||||||
1 |
|
| l |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| B |
|
|
|
|
|
| |||||
Эта формула справедлива для точек вдали от |
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
торцов катушки, вблизи торцов величина поля в |
|
|
|
| l |
|
|
|
| |||||||||||
|
|
|
|
|
|
|
| |||||||||||||
два раза меньше. Магнитное поле катушки похоже |
|
|
|
|
|
| ||||||||||||||
на магнитное поле постоянного магнита цилинд- | Рис. 15.8 | |
рической формы, см. рис. 15.1, в). Также как и там, | ||
|
на рис. 15.8 южный полюс слева, а северный – справа.
Если соленоид свернуть в кольцо, получится тороид (тор). Поле внутри тора можно посчитать по формуле (15.8), а поле снаружи равно нулю.
Для витка с током I, да и для катушки тоже, можно ввести понятие маг-
нитный момент pm, рис. 15.9. Это векторная величина, равная |
| |||
pm = IS n , | (15.9) | S | ||
где S – площадь витка, а nr – единичный вектор нормали к по- I | n | |||
верхности витка. Измеряется в А·м2. |
|
|
| pm |
Тогда формулу (15.7) можно записать в виде |
|
| ||
Br = 2k | pm | , | (15.7)″ | Рис. 15.9 |
|
| |||
1 | r3 |
|
| |
где r2 = R2 + r 2 . |
|
0 |
|
Если этот виток находится в магнитном поле B , то на него действует ме- | |
ханический вращающий момент сил M , равный |
|
M = [prm B]. | (15.10) |
Эта формула объясняет вращение якоря2 электродвигателя при включении тока.
1Длина катушки много больше ее диаметра.
2Якорь – это, по существу, катушка сложной формы, находящаяся в поле постоянных магнитов.
101

