Интересное о геометрии — МКОУ СОШ №10 х.Перевальный

От Директор 06.08.2020Дистанционный лагерь «Школа интересных наук»

Здравствуйте, ребята. И вновь с вами я — учитель математики Асанова Аминат Аргуновна.

Сегодня мы поговорим о геометрии.

Геометрия — важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано, прежде всего, с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур. 

Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик), от которого произошли также слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус», а термин «линия» возник от латинского «линум» (льняная нить). И факты геометрии сначала имели опытное происхождение.

Еще 5 тыс. лет назад древние египтяне знали, что если сделать на веревке 12 узелков на равных расстояниях и натянуть ее в форме треугольника, то получится прямой угол. И это было очень важно для правильной разметки плодородных земель в долине Нила. В египетских папирусах и вавилонских клинописных таблицах того времени мы находим другие геометрические факты, найденные опытным путем при измерении земельных участков, постройке зданий и т.д.

А в V в. до н.э. произошел решительный поворот в развитии геометрии.. И связан он с именем Фалеса, уроженца города Милет. Этот купец в свободное время занимался математикой. И сделал величайшее открытие: обнаружил, что многие геометрические закономерности можно получать не опытным путем, а с помощью рассуждения (доказательства). Это формулируют так: накрест лежащие углы, получающиеся при пересечении двух параллельных прямых третьей прямой, равны. Фалес доказал и ряд других теорем. Благодаря его открытию геометрия к III в. до н. э. становится наукой, в которой имеется небольшое число аксиом (первоначальных предположений), а все остальные факты (теоремы) устанавливаются с помощью доказательств.

За Фалесом большой вклад в развитие геометрии внесли Евдокс, Евклид, Архимед.

И, вообще, говоря. словами великого итальянского ученого Г. Галилея, «геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Если намотать вплотную (в виде спирали) веревку сначала на полусферу, а затем свернуть ее внутри круга такого же радиуса (рисунок), то окажется, что для полусферы нужна веревка вдвое длиннее. Это показывает, что площадь полусферы в два раза больше круга. Конечно, это не доказательство, а лишь опытное подтверждение данного факта. Но греческие ученые нашли и математическое доказательство.

Древнегреческий ученый Эратосфен с помощью геометрии измерил длину окружности земного шара. Он обнаружил, что, когда Солнце стоит в Сиене (Африка) над головой, в Александрии, расположенной в 800 км, оно отклоняется от вертикали на 7 . Эратосфен заключил, что из центра Земли Солнце видно под углом 7 и, следовательно, окружность земного шара равна 360 :7 ∙ 800=41 140 км.

Свыше двух тысячелетий Евклид, давший особенно удачное и стройное изложение геометрии, был непререкаемым законодателем в этой области математики. Немецкий философ И. Кант считал геометрию Евклида единственно возможной. Было, однако, место в евклидовом изложении геометрии, которое не удовлетворяло математиков. Это единственность параллельной к данной прямой, которую можно провести в плоскости через данную точку А. Евклид считал это положение аксиомой, некоторые математики пытались доказать этот факт как теорему. Однако проходили века, а доказательства найти не удалось.

Решил загадку параллельности профессор Казанского университета Н. И. Лобачевский, который опубликовал свое открытие в 1826 г. Несколько позже к тем же выводам пришли венгерский математик Янош Бояи и немецкий «король математики» К. Гаусс. Эти ученые установили, что единственность параллельной невозможно доказать как теорему. Ведь если допустить возможность провести через точку более одной прямой, не пересекающейся с данной, то мы придем к другой геометрии, неевклидовой, в которой, однако, не будет никаких противоречий.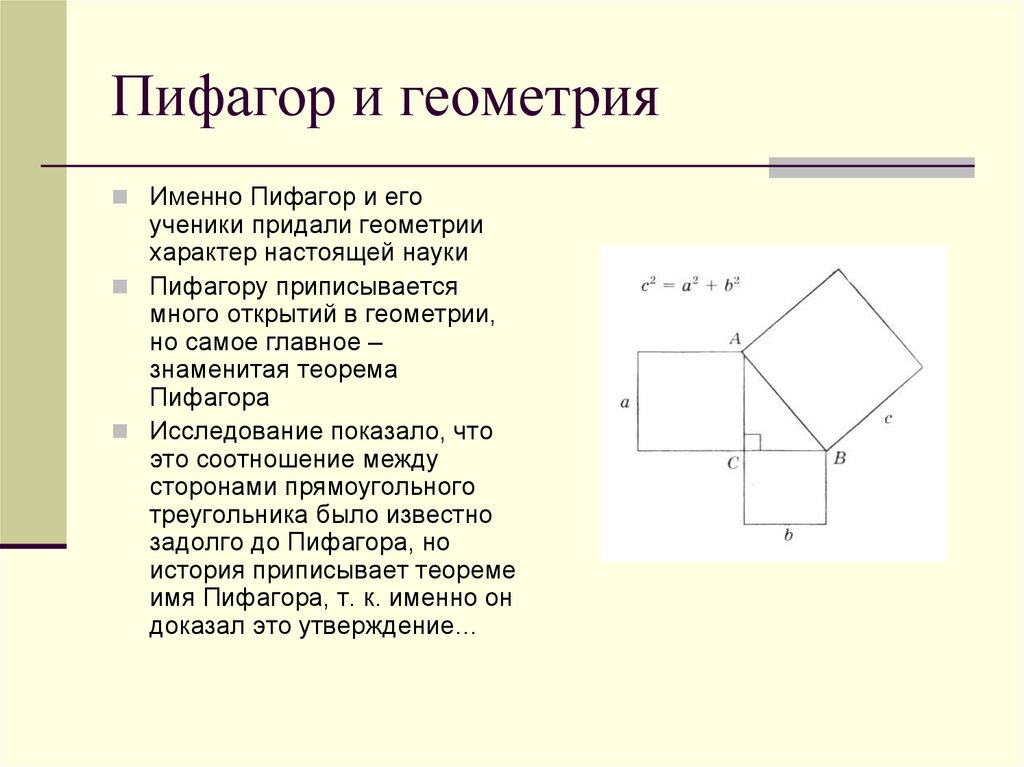

Эту геометрию называют сегодня геометрией Лобачевского.

Заменив аксиому параллельности противоположным утверждением (при сохранении остальных аксиом Евклида), мы придем к новой геометрии, которая во многом не согласуется с нашими привычными наглядными представлениями, но тем не менее не содержит никаких логических противоречий. Все трое ученых не только были убеждены в справедливости этой идеи, но и доказали десятки теорем неевклидовой геометрии. Особенно существенно развил ее Лобачевский.

В геометрии Лобачевского сумма углов любого треугольника меньше 180 .

Два перпендикуляра к одной прямой все дальше отходят друг от друга. И еще много фактов есть в этой геометрии, не похожих на те, о которых говорится в школьных учебниках. И все же никаких противоречий в этой геометрии нет. А вскоре математики открыли много других геометрий. И все они нужны. А евклидова геометрия, которую изучают в школе, — самая простая из всех и в то же время самая нужная.

Если вам интересно, то в школе у меня много интересной литературы по математике- поделюсь.

Ребята, я прощаюсь на сегодня, не забывайте о правилах дородного движения и здоровом образе жизни. 06.08.2020 год

 

Интересные факты о геометрии — Музей фактов

Новые факты теперь можно читать в Телеграме, Инстаграме и Твиттере.

Каким своим открытием больше всего гордился Архимед?

Самым важным своим достижением Архимед считал не названный его именем закон гидростатики и не устройства, которые помогли победить осадивших Сиракузы римлян. Больше всего он гордился открытием того, что объёмы шара и описанного вокруг него цилиндра соотносятся как 2:3. Архимед даже завещал поместить на его могиле скульптуру из вписанного в цилиндр шара, которую упомянул посетивший Сиракузы два века спустя Цицерон.

Источник: Wikipedia / Archimedes

Архимед геометрия Древний Рим математика могилы Сиракузы учёные

Почему нельзя точно измерить береговую линию?

Парадоксом береговой линии называют невозможность точного измерения кривых на картах — будь то береговая линия или граница между территориями. Для такого измерения нужно выбрать масштаб и аппроксимировать кривую, то есть соединить её точки прямыми отрезками равной длины (например, один километр). Однако изгибы рельефа встречаются на любом масштабе, и чем меньше размер отрезка, тем больше будет итоговая длина, а при спускании на атомарный уровень измерений эта длина будет стремиться к бесконечности. Поэтому в разных справочниках, где есть таблицы ранжирования государств по длине береговой линии, эти длины и порядок ранжирования могут кардинально отличаться друг от друга как раз по причине выбора масштаба, хотя на первом месте неизменно располагается Канада.

Источник: Википедия / Парадокс береговой линии, Википедия / Список стран по длине береговой линии

берега география геометрия границы измерения Канада картография математика парадоксы

Почему пчелиные соты состоят из шестигранников?

Построение пчелиных сот из шестигранников оптимально с точки зрении оптимизации: для хранения того же количества мёда в трёх- или четырёхгранных сотах потребовалось бы больше строительного материала.

Однако пчёлы изначально делают не шестиугольные, но круглые соты, а просветы между ними запечатывают воском. Нагреваясь от тепла пчелиных тел, воск становится вязким и начинает медленно течь. Он выдавливается из стыков под действием сил поверхностного натяжения, стенки постепенно становятся плоскими, а цилиндры сот превращаются в шестиугольные призмы.

Источник: Популярная механика / Секрет формы пчелиных сотов: Поверхностное натяжение

геометрия мед насекомые природа пчёлы

Что происходит с параллельными прямыми в геометрии Лобачевского?

По распространённому мнению, в геометрии Лобачевского параллельные прямые пересекаются. На самом деле, они не могут пересекаться ни в какой геометрии в силу самого определения параллельности. Главным же отличием геометрии Лобачевского от евклидовой является то, что через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две не пересекающих её прямых, находящихся в той же плоскости.

Источник: Википедия / Геометрия Лобачевского

геометрия заблуждения Лобачевский математика

Каким сверлом можно просверлить квадратное отверстие?

Треугольник Рёло — это геометрическая фигура, образованная пересечением трёх равных кругов некоего радиуса с центрами в вершинах равностороннего треугольника со стороной, равной этому радиусу. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с неточностью примерно в 2%).

Источник: Википедия / Кривая постоянной ширины

геометрия математика ремонт

Почему главное здание Министерства обороны США имеет форму пентагона?

В облик главного здания Министерства обороны США не закладывалась какая-либо символика. Выбор места для него пал на участок в пригороде Вашингтона Арлингтоне, на правом берегу реки Потомак, который имел форму неправильного пятиугольника. Однако из-за опасений, что здание закроет вид на Вашингтон с Арлингтонского национального кладбища, место строительства перенесли. Но проектирование уже началось, поэтому общую форму строения решили оставить как есть. А так как новый участок не был строго ограничен дорогами, пятиугольник сделали правильным — так и появился Пентагон.

Источник: Wikipedia / The Pentagon

Арлингтонское национальное кладбище архитектура Вашингтон геометрия Пентагон строительство США

Опишите орфографическую или смысловую ошибку:

Перед отправкой опровержения обязательно прочитайте источник к факту!

Ваш email:

Указывать необязательно, но желательно для диалога при опровержении факта

Спасибо! Ваше сообщение отправлено администратору.

К сожалению, что-то пошло не так. Пожалуйста, сообщите администратору по почте.

Просто скопируйте картинку и вставьте в любое место.

35 занимательных фактов о геометрии – Math2089

Дух подлинной математики, т. е. ее методы, понятия и структура, в отличие от бездумных вычислений составляет одно из лучших выражений человеческого духа. Великие области математики — алгебра, теория чисел, комбинаторика, действительный и комплексный анализ, топология, геометрия, тригонометрия и т. д. — возникли из опыта человека в отношении мира, который сотворил и в настоящее время создал бесконечный, личный, Триединый и Суверенный Бог. поддерживает. Эти разделы математики, конструктивно разработанные человеком, созданным по образу Божию, позволяют человеку систематизировать заданный порядок и связность (единство в многообразии… близкое единое и многое) творения, опосредованные нам Творцом и держателем всего. вещи – логос и премудрость Божия, явившиеся в лице Господа Иисуса Христа. Эта систематизация не только дает человеку инструмент, с помощью которого он может эффективно владычествовать над творением под руководством Бога во Христе, но также дает человеку опыт и наслаждение богатой интеллектуальной красотой, которая граничит с возвышенным в его бесконечно сложной, но структурированной мозаике.
Джеймс Никель

Геометрия — увлекательный раздел математики, который веками увлекал математиков, исследуя формы, размеры и взаимное расположение объектов. Тем не менее, в нашей повседневной жизни мы часто сталкиваемся с многочисленными геометрическими фигурами, не задумываясь об их математическом значении.

Возьмем, к примеру, пиццу, которая обычно имеет круглую форму, подается в квадратной коробке и нарезана на треугольные кусочки. Геометрия, стоящая за этим, интригует, и в этом посте мы углубимся в 35 такие чудеса геометрии которые окружают нас в повседневной жизни.

Геометрия, происходящая от греческого (γεωμετρία) слова Geometron , представляет собой изучение свойств и взаимосвязей точек, линий, форм и пространств. Термин гео относится к Земле, а метрон означает измерение.

Максимальное количество точек пересечения между двумя отдельными линиями равно одной, потому что две разные линии должны пересекаться ровно в одной точке или не пересекаться вообще.

Сумма внутренних углов треугольника равна 180 градусам. Это свойство известно как свойство суммы углов треугольника .

Стандартный футбольный мяч (также известный как футбольный мяч) состоит из 32 панелей, которые обычно представляют собой шестиугольники и пятиугольники. В частности, на стандартном футбольном мяче 12 пятиугольников и 20 шестиугольников.

Сумма противоположных граней игральной кости всегда равна 7. Например, если на одной стороне выпало 6 точек, на противоположной стороне будет 1 точка, а их сумма всегда будет равна 7.

Центр окружности уникален, и для определения уникальности окружности нам нужно как минимум три не лежащих на одной прямой точки.

Вы когда-нибудь замечали, что ячейки внутри ульев имеют шестиугольную форму? Интересно, что каждая восковая ячейка может немного различаться по размеру, но все они одинаковы по своей основной форме, которая представляет собой шестиугольник. Эта форма является отличительной чертой сот, которые создают пчелы для хранения своих личинок, меда и пыльцы.

Сумма внутренних углов четырехугольника равна 360 градусам. Это свойство известно как Свойство суммы углов четырехугольника .

Примечание . Сумма внутренних углов для n -стороннего многоугольника равна ( n – 2) × 180º.

Семь мостов Кенигсберга — известная задача, названная в честь города Кенигсберга, который был соединен с двумя большими островами семью мостами. Задача, впервые поставленная в 1736 году Леонардом Эйлером, спрашивала , можно ли найти прогулку по городу, которая пересекала бы каждый мост ровно один раз и заканчивалась в начальной точке 9. 0004 . Эйлер доказал, что такая прогулка невозможна , заложив основы современной области теории графов.

Отношение расстояния между кончиком пальца и локтем к расстоянию между локтем и запястьем часто называют примерно равным золотому сечению ф  ( фи ), что примерно равно 1,618 .

Эта формула названа в честь математика Леонарда Эйлера, который впервые открыл ее в 18 веке. В любом выпуклом многограннике (трехмерном теле с плоскими многоугольными гранями) число его вершин ( V ), ребра ( E ) и грани ( F ) связаны уравнением:

Разрезание бутерброда по диагонали на две треугольные половины традиционно более распространено, чем разрезание на две прямоугольные половины. Нет однозначного ответа, почему бутерброды традиционно разрезают по диагонали, но есть несколько возможных причин. Во-первых, если сэндвич разрезать пополам по диагонали, его будет легче держать и есть. Во-вторых, сэндвич, разрезанный по диагонали, часто воспринимается как более привлекательный, чем сэндвич, разрезанный поперек. Наконец, диагональный разрез может создать иллюзию того, что бутерброд больше, что может сделать его более привлекательным для еды.

Теорема о сумме внешних углов в геометрии утверждает, что сумма внешних углов многоугольника всегда равна 360 градусам. Независимо от того, является ли многоугольник треугольником, четырехугольником, шестиугольником или десятиугольником, сумма его внешних углов остается постоянной.

Яйца нельзя классифицировать как круглые или эллиптические по форме, так как они имеют овальную форму. В частности, куриные яйца являются ярким примером овалов. Если вы внимательно посмотрите на яйцо, расстояние от центра не будет фиксированным кругом. Горизонтальный аспект имеет более длинную форму эллипса. Если еще раз внимательно присмотреться, то одно горизонтальное направление округло изогнуто, а другое заострено. Это форма яйца.

Имея две точки A и B на вертикальной плоскости, какую кривую описывает точка, на которую действует только сила тяжести, которая начинается в A и достигает B за кратчайшее время? Эта классическая задача известна как проблема брахистохроны, которая была поставлена ​​и решена Бернулли в 1696 г. Кривая наискорейшего спуска — не прямая и не ломаная, а циклоида.

Отношение длины окружности любого круга к его диаметру является постоянной величиной, известной как 9.0006 pi ( π ), что примерно равно 3,14. Пи — иррациональное число. День Пи отмечается 14 марта года ( 3 / 14 ), что является отсылкой к первым трем цифрам числа Пи.

Картофельные чипсы бывают разных форм и размеров, но чипсы Pringles уникальны благодаря своей седловидной форме, которая представляет собой гиперболический параболоид. Эта форма была выбрана потому, что она позволяет равномерно укладывать чипсы в канистру, максимально увеличивая пространство для хранения и сводя к минимуму поломку. Кроме того, седловидная форма гарантирует, что каждая стружка будет равномерно прожариваться в процессе производства, что приведет к неизменному вкусу и текстуре.

При пересечении двух прямых секущей соответствующих углов образуются на одних и тех же сторонах секущей, а чередующихся углов образуются на противоположных сторонах секущей.

Математики определили, что существует только 17 различных типов плоскостной симметрии, которые могут встречаться в повторяющемся узоре обоев. Однако важно отметить, что внутри каждой из этих 17 групп существует множество возможных вариаций цвета, текстуры и других декоративных элементов.

Мы сможем вместить больше песка, если сделаем цилиндр меньшей высоты и большего радиуса по сравнению с цилиндром большей высоты и меньшего радиуса, используя бумагу размера A ₄ .

Типичные потолочные вентиляторы имеют три лопасти, каждая из которых наклонена к соседней под углом 120°. 3 лопасти расположены под одинаковыми углами, так что результирующая сила, которую они прикладывают, становится равной 0, и в любом направлении не остается никакой силы.

Мороженицы имеют вид полых тонкостенных конусов с круглым основанием или иногда усеченного прямоугольного конуса (из пшеничной и кукурузной муки). Цель состоит в том, чтобы эффективно удерживать мороженое. Если шарики мороженого можно представить в виде сфер, то конус будет содержать наибольшее количество вкусного мороженого и наименьшее количество воздуха.

Существует 43252003274489856000 возможных конфигураций кубика Рубика. Каждую конфигурацию кубика Рубика можно собрать за 20 ходов или меньше. Это известно как Число Бога. Кубик Рубика 3 × 3 × 3 содержит 26 уникальных миниатюрных кубиков, также известных как кубики (или кубики).

Часовая и минутная стрелки часов перпендикулярны друг другу 44 раза в сутки.

1 радиан больше 1 градуса. На самом деле 1 радиан примерно равен 57,2958º.

Задача о висячей цепи — это классическая задача математики, которая заключается в нахождении формы висячей цепи, подвешенной между двумя точками под действием силы тяжести. Решение дается контактной сетью, которая представляет собой кривую, имеющую форму, подобную параболе, но более широкую и плоскую, и обеспечивает устойчивое равновесие для висящей цепи.

Основными несущими конструкциями воздушных линий электропередачи являются опоры. Башни электропередач рассчитаны на то, чтобы выдерживать вес тяжелых кабелей электропередач и поднимать их над землей. Треугольные формы часто используются в таких конструкциях, как электрические опоры (известные как траверсы ), поскольку они жесткие и устойчивые. Форма треугольника распределяет силы равномерно, что делает его более прочным и устойчивым к изгибу или разрушению по сравнению с четырехугольником. Кроме того, в треугольных конструкциях используется меньше материала для достижения того же уровня устойчивости, что делает их строительство более рентабельным.

Куб Метатрона соединяет тринадцать кругов в форме Плода Жизни с прямыми линиями и содержит все пять Платоновых Тел , представляющих универсальные геометрические узоры.

Если мяч брошен под углом 45 градусов к горизонту, он пролетит максимально возможное расстояние.

Чтобы разделить данную фигуру на восемь частей, требуется минимум трех разрезов. Эти три разреза должны быть сделаны по горизонтали , по вертикали , а по основанию .

Международные размеры бумаги, такие как A ₃ , A ₄ и другие, основаны на квадратном корне из 2. Размеры бумаги размера A ₄ составляют 210 мм. 297 мм, а для бумаги формата A ₃ — 297 мм × 420 мм. Если предположить, что высота больше ширины, то отношение высоты к ширине всех форматов равно √2 или 1,414. Соединение двух A _{4 бумаги размера} дадут одну бумагу размера A ₃ , две бумаги размера A ₃ дадут вам одну бумагу размера A _2, и так далее.

Асимптота кривой представляет собой линию, расстояние между которой и линией стремится к нулю, когда одна или обе координаты x или y стремятся к бесконечности. Слово происходит от греческого ἀσύμπτωτος. Существует три вида асимптот: горизонтальный , вертикальный и наклонный .

Платоново тело — это трехмерная фигура, каждая грань которой аналогична правильному многоугольнику и имеет такое же количество граней, сходящихся в каждой вершине. Платоновых тел всего пять: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Впервые их обнаружил древнегреческий философ Платон, считавший, что они представляют пять элементов вселенной: землю, воздух, огонь, воду и эфир.

Если две прямые линии не параллельны и не пересекаются, в трехмерной геометрии они называются косыми линиями. Две прямые скошены тогда и только тогда, когда они не лежат в одной плоскости. Поскольку две линии на плоскости должны пересекаться или быть параллельными, скрещивающиеся линии могут существовать только в трех и более измерениях.

Обычно пицца круглая , имеет квадратную коробку для доставки, но разрезается на треугольников . Пицца в основном круглая, так как это позволяет равномерно готовить и распределять тепло в круглой печи, в результате чего получается вкусная и равномерно приготовленная пицца. Квадратные коробки для пиццы более практичны и экономичны, поскольку они аккуратно помещаются, легко складываются и занимают меньше места при транспортировке, чем круглые коробки. Кроме того, они проще и дешевле в производстве. Нарезка пиццы на треугольные ломтики практична и удобна, так как обеспечивает равные порции начинки и корочки, максимально увеличивает количество ломтиков и позволяет легко делиться и контролировать порции.

Этот блог принадлежит вам не меньше, чем мне. Итак, если у вас есть какие-то идеи, чтобы поделиться тем, что вы хотите увидеть в следующем посте, не стесняйтесь написать. Мы приветствуем ваши идеи с распростертыми объятиями и благоговением! Ждем вас в ближайшее время на « Math2089 – Математика для всех » для еще одного увлекательного блога по математике.

Нравится:

Нравится Загрузка…

Геометрия

Геометрия это все о формы и их свойства.

Если вы любите играть с предметами или рисовать, то геометрия для вас!

Геометрию можно разделить на:

Плоская геометрия касается плоских фигур, таких как линии, круги и треугольники… формы, которые можно нарисовать на листе бумаги

 

Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.

Подсказка: попробуйте нарисовать некоторые формы и углы, когда будете учиться… это поможет.

Точка, линия, плоскость и тело

Точка не имеет размеров, только положение
Линия одномерная
Плоскость двухмерная (2D)
Твердое тело трехмерное (3D)

Почему?

Почему мы занимаемся геометрией? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать окружающий мир.

Плоская геометрия

Плоская геометрия — это формы на плоской поверхности (как на бесконечном листе бумаги).

• 2D-фигуры
• Упражнение: Сортировка фигур
• Треугольники
• Прямоугольные треугольники
• Интерактивные треугольники

 

• Четырехугольники (ромб, параллелограмм, и т.д.)
• Прямоугольник, ромб, квадрат, параллелограмм, трапеция и воздушный змей
• Интерактивные четырехугольники
• Параллелограмм в любом четырехугольнике
• Форматы бумаги
• Свободная игра фигур

• Периметр

• Зона
• Площадь плоских фигур
• Инструмент расчета площади
• Площадь многоугольника по чертежу
• Деятельность: Сад

• Общий инструмент для рисования
• Калькулятор площади и калькулятор прямоугольника

Полигоны

Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники являются многоугольниками.

Вот еще:

Пентагон

Пентаграмма

Шестигранник

 

• Свойства правильных многоугольников
• Диагонали многоугольников
• Интерактивные полигоны

 

Круг

• Круг
• Пи
• Площадь круга по линиям
• Круговой сектор и сегмент
• Площадь круга по секторам
• Упражнение: бросание монеты на сетку
• Арка
• Кольцо

Теоремы о кругах (дополнительная тема)

 

Символы

В геометрии используется много специальных символов. Вот краткая ссылка для вас:

Геометрические символы

 

Конгруэнтные и аналогичные

• Конгруэнтные формы
• Похожие фигуры

 

Уголки

Типы уголков

Острые углы

Прямые углы

Тупые углы

Прямой угол

Рефлекторные углы

Полный оборот

Градусы (угол) радиан Равные углы Параллельные прямые и пары углов Поперечный Смежные углы Треугольник имеет 180° Дополнительные уголки Дополнительные углы

Углы вокруг точки Углы на прямой линии Внутренние уголки Наружные углы Внутренние углы многоугольников Внешние углы многоугольников

Использование чертежных инструментов

• Геометрические конструкции
• Использование транспортира
• Использование чертежного треугольника и линейки
• Использование линейки и компаса

 

Преобразования и симметрия

Преобразования:

• Вращение
• Отражение
• Перевод
• Изменение размера

Симметрия:

• Симметрия отражения
• Вращательная симметрия
• Точечная симметрия
• Линии симметрии плоских фигур

• Художник по симметрии

• Упражнение: Симметрия фигур
• Упражнение: Создание мандалы
• Упражнение: Раскрашивание (Четыре цвета Теорема)

• Мозаика
• Мастер тесселяции

 

Координаты

• Декартовы координаты
• Интерактивные декартовы координаты
• Игра «Найди координаты 9»0314

 

 

Дополнительные темы плоской геометрии

Пифагор

• Теорема Пифагора
• Пифагорейские тройки

 

Конические секции

• Набор всех точек
• Конические секции
• Эксцентриситет
• Эллипс
• Анимация параболы и снаряда
• Гипербола

 

Теоремы о кругах

• Теоремы о кругах
• Касательные и секущие линии
• Теорема о пересекающихся секущих
• Теорема о пересекающихся хордах
• Угол пересекающихся секущих Теорема

Треугольные центры

Тригонометрия

Тригонометрия — отдельная тема, поэтому вы можете посетить:

• Введение в тригонометрию
• Указатель тригонометрии

 

Твердотельная геометрия

Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…

.