20 интересных фактов о геометрии

Наука геометрия, изобретённая тысячи лет назад, с тех пор продолжает развиваться и меняться, но основы её остаются теми же. Она прочно вошла в человеческую цивилизацию, являясь базой для самых разных областей. Посмотрите куда угодно, и вы увидите, что при создании того или иного предмета его авторы опирались на геометрические вычисления. Что угодно — дорога у вас под окнами, ваша квартира, мобильный телефон или книга в шкафу. Без геометрии не было бы человеческой цивилизации в том виде, в котором мы её знаем.

Факты о геометрии

• Достоверно известно, что геометрические знания применялись ещё в Древнем Египте более 5000 лет назад. Египтяне пользовались ими не только при строительстве пирамид, но и при разметке участков для посевов на берегах Нила.
• Сейчас геометрия является одним из основополагающих разделов математики. Однако, в Древней Греции она была фактически математикой в целом, а не частью её.
• Больше всего, пожалуй, для геометрии сделал античный учёный Евклид. Открытые им принципы до сих пор лежат в основе этой науки (интересные факты о Евклиде).
• Над дверью в школу, в которой древнегреческий учёный и философ Платон учил своих учеников, красовалась надпись «Пусть не входит сюда тот, кто не знает геометрии».
• Трапеция — одна из геометрических фигур. Но слово это произошло от древнегреческого «трапезион», что в переводе означает «столик». А слово «конос», от которого произошло наше «конус», означало «сосновая шишка».
• Среди всех геометрических форм с одинаковым периметром, круг имеет наибольшую площадь и, наоборот, среди всех фигур с одинаковой площадью круг имеет наименьший периметр.
• При помощи геометрических правил и предположения о том, что наша земля шарообразна, древнегреческий ученый Эратосфен измерил длину её окружности. Как показали измерения современных учёных, он практически не ошибся в своих расчётах, погрешность составляла лишь доли процента.
• Основы фрактальной геометрии были заложены знаменитым учёным эпохи возрождения Леонардо да Винчи (интересные факты о Леонардо да Винчи).
• Основное отличие геометрии Лобачевского от евклидовой заключается в утверждении, что через одну точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере 2 не пересекающих её прямых, находящихся в той же плоскости.
• В геометрии Лобачевского сумма всех углов треугольника составляет меньше 180 градусов.
• Существуют и другие виды неевклидовых геометрий. Они не применяются в повседневной жизни, но помогают решить множество вопросов в других науках, например, в астрономии.

• Теорему Пифагора называли «ослиным мостом», потому что учеников, которые запоминали теорему без понимания, называли ослами, по той причине, что они не могли «перейти через мост» — теорему Пифагора.
• Когда Пифагор доказал свою теорему, надстроив прямоугольный треугольник квадратами по его сторонам, его шок и потрясение учеников были так велики, что ученики решили — мир уже познан, осталось только объяснить его числами (интересные факты о Пифагоре).
• Архимед, которому Александрия была не чужда, хоть он и родился в Сиракузах, изобрёл немало механических устройств, но своим главным достижением считал вычисление объёмов конуса и шара, вписанных в цилиндр. Объём конуса составляет одну треть от объёма цилиндра, а объём шара — две трети.
• Еще около 5000 назад древние египтяне знали, что если сделать на веревке 12 узелков на равных расстояниях и натянуть ее в форме треугольника, то получится прямой угол. Эти знания применялись в строительстве.
• Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
• В геометрии Римана сумма углов треугольника всегда больше 180.
• Французский император Наполеон Бонапарт был прекрасным математиком, и он является автором ряда научных трудов. В его честь даже одна из геометрических задач даже была названа «задача Наполеона».
• В геометрии формула вычисления объема усеченной пирамиды выведена раньше, чем формула для целой пирамиды.
• Евклид лично доказал 465 геометрических теорем.

Категории

• Обо всём на свете

Предыдущая заметка Следующая заметка

Интересные факты о геометрии

Геометрия — удивительная наука, один из важнейших и значительных разделов математики. Она присутствует в нашей жизни повсюду: предметы, объекты, которые нас окружают, имеют форму, размер, их можно измерить, оценить расстояние между ними, расположение относительно друг друга. Эту науку начинают изучать в 7 классе. Представляем интересные факты о геометрии.

Эта наука насчитывает тысячелетия, ее возникновение связывают с необходимостью для древних египтян измерять площадь плодородных земель в долине реки Нил. Эти земли регулярно подвергались затоплению, в результате которого размывались границы, определяющие принадлежность участков конкретных владельцам. Для того, чтобы восстановить границы своих владений, египтянам приходилось производить соответствующие измерения и вычисления. Особенно внимательно к таким расчетам относились сборщики налогов на землю.

Впоследствии из Древнего Египта геометрия перекочевала в Древнюю Элладу, где получила дальнейшее развитие. Древние греки с большим почтением относились к этой науке и отождествляли ее с математикой. «Пусть сюда не входит тот, кто не знает геометрии», — такие слова встречали учеников Платона на пороге Академии.

В названиях многих геометрических фигур заключены слова, описывающие предметы, похожие на данные фигуры. Так, трапеция обязана своим названием сходству со столом, который в древнегреческом обиходе именовался «трапезион». Сосновая шишка, именуемая в греческом языке словом «конос», дала название известному нам конусу. А вот «линия» имеет латинский корень («линум» переводится как «льняная нить»).

Очень интересным по своим свойствам является круг. Если сравнивать все геометрические фигуры, имеющие одинаковый периметр, то круг будет иметь наибольшую площадь. И наоборот, если рассматривать все фигуры, имеющие одинаковую площадь, то окажется, что минимальный периметр — у круга.

Во второй половине 20 века появилось новое слово в геометрии — фракталы. Его ввел Бенуа Мандельброт, который считается основателем фрактальной геометрии, хотя сами фрактальные структуры существовали в природе задолго до этого. Ведь фракталы — это множества самоподобных элементов. Примером такого множества является красивое соцветие капусты сорта Романеско. Его бутоны расположены в соответствии со строгой логарифмической спиралью, каждый бутон, в свою очередь, состоит из более мелких бутонов, расположение которых аналогично. И эта структура повторяется многократно.

Закономерность, присущую фрактальным структурам, вывел еще известный итальянский ученый Леонардо да Винчи: если на определенной высоте измерить диаметр ствола дерева и возвести его в квадрат, то полученное значение будет равно сумме квадратов диаметров ветвей, расположенных на той же высоте. Впоследствии это было подтверждено и другими исследователями с одним уточнением: степень в формуле не всегда является квадратной, ее величина может принадлежать интервалу от 1,8 до 2,3. Описанное Леонардо да Винчи явление изначально объяснялось необходимостью обеспечения оптимальной структуры дерева, позволяющей более эффективно снабжать растение питательными соками. Позднее этому факту было предложено иное объяснение: подобная фрактальная структура дерева уменьшает вероятность того, что сильные порывы ветра могут сломать ветки.

Расположение листьев на ветке также подчинено определенному закону. Угол расхождения, который образуется между соседними листьям, для каждого растения свой, но описывается он всегда простой дробью. В числителе и знаменателе такой дроби — числа из ряда Фибоначчи, который представляет собой последовательность чисел, где каждое следующее число представляет собой сумму двух предыдущих, причем два первых — это 0 и 1, либо 1 и 1. Например, угол расположения листьев бука составляет 1/3 или 120 градусов, у абрикоса этот угол равен 2/5, у груши — 3/8, а у ивы — 5/13. Располагаясь подобным образом, листья получают оптимальный ресурс солнечного света.

Основоположником геометрии как науки является Евклид, который свыше 2000 лет назад дал наиболее логичное и стройное ее изложение в своей книге «Начала». Впоследствии его учение так и стало называться «евклидова геометрия». И только в начале 19 века некоторые ученые предположили возможность существования иной геометрии, отличной от евклидовой. Первый из них — Николай Иванович Лобачевский, профессор Казанского университета. Геометрия Лобачевского имеет в своей основе те же положения, что и «евклидова геометрия», за исключением аксиомы о параллельности прямых. В соответствии с учением Евклида, существует только одна прямая, проходящая через точку вне заданной прямой и принадлежащая той же плоскости. Это верно для плоскости, не имеющей отклонения или кривизны. Лобачевский вводит понятие плоскости с отрицательной кривизной (поэтому геометрию Лобачевского называют еще «гиперболическая геометрия»). И тогда прямые, принадлежащие этой плоскости, приобретают иные свойства, которые допускают возможность существования как минимум двух прямых, имеющих общую точку, лежащую вне данной прямой, и не пересекающих данную прямую. Следует отметить, что геометрия Лобачевского нашла отражение в теории относительности А. Эйнштейна, согласно которой пространство нашей Вселенной имеет гиперболическую форму.

Геометрия факты интересные. Интересные факты о геометрии

Геометрия факты интересные. Интересные факты о геометрии

1. Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
2. Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
3. С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
4. Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
5. Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
6. Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
7. В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
8. Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
9. Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
10. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
11. Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
12. Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
13. Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
14. При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
15. Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

Интересные факты о стереометрии. Стереометрия

Стереоме́трия (от др.-греч. «твёрдый; объёмный, пространственный» + «измеряю») — раздел евклидовой геометрии , в котором изучаются свойства фигур в пространстве. Основными (простейшими) фигурами в пространстве являются точки , прямые и плоскости . В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые . Это одно из немногих существенных отличий стереометрии от планиметрии , так как во многих случаях задачи по стереометрии решаются путём рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников . Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми . Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань .

Источник: https://interesnyefakty.com/novosti/interesnye-fakty-geometriya-interesnye-fakty-o-geometrii

Интересные факты о углах. 10 интересных фактов о математике, которые удивляют

Человек может и не быть математиком. 

Более того, он может даже не знать эту науку на минимальном уровне, но тяжело отрицать – математику человек видит практически везде. 

Цифры, фигуры и математические законы преследуют человека повсюду, поэтому нелишним будет узнать кое-что об этой науке.

1. Абрахам де Муавр (математик из Англии) в своей глубокой старости вдруг понял, что его сон увеличивается на 15 минут в каждый последующий день. После этого он составил прогрессию и определил тот день, когда сон займет весь день. Случилось это 27 ноября в 1754 году, и это был день его смерти.

2. Религиозные и верующие евреи стараются всеми силами избегать любых знаков, которые связаны с крестом или символику Христа. К примеру, вместо плюса в школах используют перевернутую «Т».

3. Подлинность денежной купюры евро всегда можно узнать по ее серийному номеру – это буква и 11 цифр. Необходимо поменять букву на то число, которое является порядковым номером этой буквы в алфавите. После этого необходимо сложить все числа и складывать результаты до тех пор, пока не будет одна цифра. И если в итоге получится 8, это говорит о подлинности купюры. Другой способ – сложение всех цифр, без буквы. Итоговый результат, состоящий их буквы и цифры, должен подходить под ту страну, на территории которой появилась купюра. К примеру, Германия – это Х2.

4. Есть версия, что Альфред Нобель отказался включать математику в длинный список наук для своей премии по личным причинам – жена Альфреда спала с математиком. Но в действительности Нобель был холостым. Нет достоверных доказательств того, почему математику не включили, однако есть предположения. К примеру, уже тогда существовала своя премия, но созданная шведским королем. Другая версия – математика является чисто теоретическим предметом, поэтому математики не способны сделать ничего действительно важного для людей и человечества в целом.

5. Есть такая фигура, как треугольник Рело. Она образовывается через пересечение трех идентичных по радиусу кругов, причем центры этих кругов расположены в вершинах треугольника с равными сторонами. Сверло, созданное на основе этого треугольника, дает возможность сверлить только квадратные отверстия. При этом стоит помнить, что сверление таких отверстий с использованием треугольника Рело может иметь погрешность в 2 процента.

6. В русской литература и математике 0 не относится к спискам натуральных чисел, однако на западе 0 является одним из представителей множества таких чисел.

7. Джордж Данциг, математик из Америки, будучи всего лишь университетским аспирантом, один раз опоздал на занятие и, увидев несколько уравнений и подумал о том, что эти уравнения являются общими домашними задачами, которые необходимо выполнить. Это задание показалось ему намного сложнее того, что давали обычно, но он их выполнил и принес результаты преподавателю. И только после этого он узнал, что смог решить 2 нерешаемых уравнения статистики. Причем это были те задачи, которые не могли решить ученые в течение нескольких лет.

8. Если сложить все числа в рулетке, получится 666.

9. Небезызвестная Софья Ковалевская познакомилась с этой наукой о числах в далеком детстве – в ее комнате не было обоев, были лишь лекции ученого Остроградского об исчислениях.

10. В Индиане (штат США) в 1897-ом году выпустили билль, согласно которому число Пи будет равно 3,2. Однако билль не превратился в закон благодаря тому, что в этот процесс вовремя вмешался университетский профессор.

Интересные факты о трапеции. Презентация 8 класса на тему: «Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина.». Скачать бесплатно и без регистрации. — Транскрипт:

---

1 Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина

2 Цели: 1.Узнать интересную информацию о геометрической фигуре «трапеция»; 2.Показать, что она встречается в нашей жизни чаще, чем нам кажется.

3 То, что мы знаем о трапеции: Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции ее средняя линия параллельна основаниям и равна их полусумме; если трапеция равнобедренная, то ее диагонали равны и углы при основании равны; / 5

4 А вот то, что мы еще не знаем: ее средняя линия равна полусумме оснований; если трапеция равнобедренная, то около нее можно описать окружность; если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

9 Задача 1. Треугольник из трапеций! Сложите из трех одинаковых трапеций равносторонний треугольник. Трапеции нельзя накладывать друг на друга, разрезать. Треугольник должен получиться целый (без отверстий внутри) и без лишних частей снаружи фигуры.

11 Задача 2. Четыре из одной! Разрежьте данную фигуру на четыре равные и одинаковые по форме части, не повторяющие, однако, исходную форму.

13 Итак: С помощью этой презентации вы узнали, как часто встречается трапеция в нашей жизни! Вы решили несколько интересных задач, связанных с трапецией. Мы надеемся, что вам было интересно!

Интересные факты о конусе. Конусы

Брюхоногие моллюски рода конус обладают раковиной, длина которой 15 20 см, а форма напоминает коническую. Раковины этих животных окрашены в красивые тона и имеют на поверхности изысканный узор, чем и привлекают коллекционеров, стремящихся заполучить такую раковину. Эти раковины привлекают внимание и охотников за моллюсками, так как на рынках они высоко ценятся туристами.

K наиболее распространенным и брюхоногих моллюсков рода конус относятся:

• , живущие в зоне от Полинезии до Индийского океана;
• , обитающий в зоне Полинезии, и вплоть, до восточного побережья Африки;
• обитающие в регионе от Красного моря до Полинезии;
• — житель берегов Австралии и восточного побережья Африки.

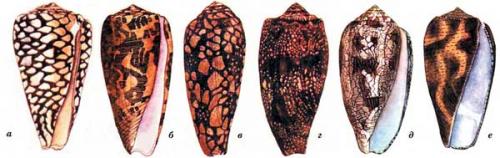
Ловцы конусов могут получить уколы от этих животных, когда они складывают моллюсков в сетчатые мешки, а также могут пострадать и при неосторожной транспортировке мешка, который они, как правило, привязывают к поясу. Сказанное относится к ловцам-профессионалам. Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.

Готовясь напасть , моллюск выдвигает зубы в переднюю часть головы, чтобы вонзить их в тело жертвы. К зубам подходит яд из канала радулы и глотки. В хоботке расположен один из зубов радулы. При уколе пузырек сжимается и яд под давлением вгоняется в свернутые, похожие на острый полый гарпун — зубы радулы.

Конусы обычно предпочитают держаться или свободно . Тропические виды этих моллюсков представляют реальную угрозу для человека, так как их яд, попавший в организм, часто вызывает гибель пострадавших. Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.

Б. Холстед считает, что при развивающихся симптомах отравления ядом расстройства дыхания обычно не бывает, а В. Н. Орлова и Д. Б. Гелашвили указывают, что в тяжелых случаях человек погибает не от остановки сердца, а от паралича дыхательной мускулатуры.

Для предупреждения поражений этими моллюсками можно порекомендовать единственный способ, а именно, быть крайне аккуратным при прикосновении к раковинам неизвестных моллюсков. Брать их необходимо очень осторожно, избегая мягких тканей животного.

15 интересных фактов о геометрии

За долгие годы, прошедшие с момента её изобретения, геометрия изменилась не так уж и значительно. Появились новые её разновидности, но сама геометрия в классическом понимании этого слова до сих пор базируется на принципах, открытых сотни и тысячи лет назад. Она является одной из фундаментальных наук, на которые опирается человечество, и переоценить её важность попросту невозможно.

Интересные факты о геометрии

1. Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
2. Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
3. С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
4. Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне).
5. Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
6. Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
7. В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
8. Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
9. Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами (25 интересных фактов о Пифагоре).
10. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
11. Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
12. Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
13. Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
14. При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
15. Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

Интересное о геометрии. «Школьная газета » Интересные факты о геометрии»

Интересное о геометрии. «Школьная газета » Интересные факты о геометрии»

Интересные факты о геометрии.Слово «трапеция» произошло от древнегреческого слова «трапезион»(обозначает столик). также от данного слова произошли уже немногоподзабытые в обиходе слова, такие как «трапеза» и прочие родственныеему слова.Математика для древних греков была, прежде всего, геометрией.Поэтому над двери Академии, в стенах которой Платон учил своих учеников, висела надпись: «Пусть сюда не входит тот, кто не знает геометрии».Греческое слово «конос», обозначающее сосновую шишку, является словарной основой для такого термина как «конус», а известный в геометрии термин «линия» возник уже от латинского слова «линум» (что в переводе на русский язык означает «льняная нить»).Пирог разрезается всего тремя касаниями ножа на восемь равных долей. Причем, существует только два способа это сделать. Под треугольником Рёло понимают геометрическую фигуру, образованную пересечением 3 кругов одинакового радиуса D с центрами, находящимися в вершинах равностороннего треугольника, такой же по длине стороны. на основе треугольника Рёло было придумано сверло, позволяющее просверливатьпочти квадратные отверстия. В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180. В геометрии Римана сумма углов треугольника всегда больше 180.Если число 111 111 111 помножить на себя самого, то получится интересное число 12 345 678 987 654 321 (все числа сначала возрастают, а потом убывают по порядку).Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.Еще факты Знаете ли вы? Что Шарль Перро, автор «Красной Шапочки», написал сказку «Любовь циркуля и линейки»?   Что Наполеон Бонапарт писал математические труды и один геометрический факт называется «Задача Наполеона»?   Что Пифагор был победителем из кулачного боя на 58-х Олимпийских играх, проходивших в 548 году до н. э., а затем побеждал еще на нескольких Олимпиадах? Выполнил Меркулов Лев,Педагог Меркулова О.Р.

Интересные факты о треугольниках в геометрии. Интересные факты о геометрии

1. Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
2. Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
3. С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
4. Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
5. Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
6. Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
7. В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
8. Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
9. Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
10. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
11. Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
12. Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
13. Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
14. При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
15. Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

Интересные факты о углах. Интересные факты об угле

Человек использует уголь в качестве топлива с древнейших времен. С момента изобретения его использовали для самых разных целей. Это было и приготовление еды, и промышленное производство. Благодаря углю стало возможно изготавливать сталь. С углем связано множество интересных фактов, а его роль в нашей жизни колоссальна.

Образование угля в недрах земли – очень долгий процесс. Здесь много общего с нефтью. Уголь образуется из погибших растений, которые по тем или иным причинам оказывались под землей. Здесь без кислорода они не гнили, и их остатки не теряли содержавшийся в них углерод – основу угля. Далее в течение миллионов лет под воздействием самых разных факторов эти остатки превращались в торф, а из него в уголь. А дальнейший процесс приводит к образованию графита.Прежде, чем углубляться в интересные факты о технология добычи и интересных ситуаций, связанных с углем, поговорим об углях, необходимых для приготовления пищи:Вообще основное отличие японской кухни от европейской – доминирование морепродуктов. Их используют повсеместно. И даже для шашлыков, которые японцы называют «тэмпора». Правда, при этом они не очень часто используют уголь для их приготовления. Считается, что он способен впитывать запахи и затем отдавать их готовящемуся блюду. Углю в основном предпочитают открытый огонь. А в дополнение часто используют имбирь, который также устраняет запахи.

В Северной Африке во франкоговорящих странах любят использовать сухой кустарники и прочие мелкие растения. Здесь пустыня, и крупных деревьев нет. Угли делают, например, из саксаула. Они получаются горячими и обладающими специфическим ароматом.

У нас же в России привычнее использовать уголь для шашлыка в брикетах. Лично от себя могу посоветовать компанию «Добрый уголь», которая специализирутеся на производстве угля для кальяна и барбекю наивысшего качества.

Шахты, в которых добывают уголь, являются довольно опасным местом. В них выделяются различные газы. Особо опасен метан. Он вытесняет часть кислорода и делает воздух взрывоопасным. Раньше, когда индикаторов метана не существовало, использовали канареек. Их брали с собой в шахту, и если птицам становилось плохо, это означало, что в шахте скопился метан.

Среди других опасностей выделяются пожары в шахтах. Как в случаях с горящим торфом, они могут длить достаточно долго. Рекордным получился пожар на месторождении Люхуангоу в Китае. На его устранение ушло целых 130 лет, и окончательно его потушили только в 2004 году. Было уничтожено около 260 млн. тонн угля.

С углем и его месторождениями связано множество забавных ситуаций. В нем часто находили сокровища. Так в 1891 году повезло некой госпоже Калп, нашедшей в большом куске угля старинную золотую цепочку. Уголь хранит множество древних артефактов. Шахтеры не раз находили останки древних сооружений. Как, например, в американском городке Хаммондвилле, где в 1869 году нашли останки стены с иероглифами.

Уголь продолжает играть большую роль в жизни людей и даже целых городов. Интересно проследить судьбу японского города Хасима, находящегося на одноименном острове, который был некогда богат углем. Начиная с 30-х годов века прошлого, этот город долгое время считался самым густонаселенным в мире. Остров обладал береговой линией всего в 1 км, но его население составляло более 5 тыс. человек. Но к середине 70-х уголь здесь закончился. Люди начали покидать это место. Город стал абсолютно заброшенным. Сейчас там даже проводят экстремальные экскурсии.

В России находятся огромные запасы угля. Ученые заявляют о 4 триллионах тонн запасов. Это чуть менее трети от общемировых.

Уголь может иметь не только привычную твердую форму. Сегодня имеются технологии, превращающие его в жидкое топливо, очень похожее на нефть.

В промышленности уголь используют не только в качестве топлива. Он является сырьем для производства различных материалов. Например, из каменного угля делают искусственный графит. А еще из угля добывают содержащиеся в нем полезные материалы: свинец, серу, галлий, цинк и другие.

Источник: https://interesnyefakty.com/novosti/geometriya-fakty-interesnye-interesnye-fakty-o-geometrii

Интересные факты о конусе. Конусы

Брюхоногие моллюски рода конус обладают раковиной, длина которой 15 20 см, а форма напоминает коническую. Раковины этих животных окрашены в красивые тона и имеют на поверхности изысканный узор, чем и привлекают коллекционеров, стремящихся заполучить такую раковину. Эти раковины привлекают внимание и охотников за моллюсками, так как на рынках они высоко ценятся туристами.

K наиболее распространенным и брюхоногих моллюсков рода конус относятся:

• , живущие в зоне от Полинезии до Индийского океана;
• , обитающий в зоне Полинезии, и вплоть, до восточного побережья Африки;
• обитающие в регионе от Красного моря до Полинезии;
• — житель берегов Австралии и восточного побережья Африки.

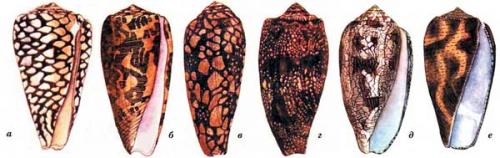
Ловцы конусов могут получить уколы от этих животных, когда они складывают моллюсков в сетчатые мешки, а также могут пострадать и при неосторожной транспортировке мешка, который они, как правило, привязывают к поясу. Сказанное относится к ловцам-профессионалам. Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.

Готовясь напасть , моллюск выдвигает зубы в переднюю часть головы, чтобы вонзить их в тело жертвы. К зубам подходит яд из канала радулы и глотки. В хоботке расположен один из зубов радулы. При уколе пузырек сжимается и яд под давлением вгоняется в свернутые, похожие на острый полый гарпун — зубы радулы.

Конусы обычно предпочитают держаться или свободно . Тропические виды этих моллюсков представляют реальную угрозу для человека, так как их яд, попавший в организм, часто вызывает гибель пострадавших. Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.

Б. Холстед считает, что при развивающихся симптомах отравления ядом расстройства дыхания обычно не бывает, а В. Н. Орлова и Д. Б. Гелашвили указывают, что в тяжелых случаях человек погибает не от остановки сердца, а от паралича дыхательной мускулатуры.

Для предупреждения поражений этими моллюсками можно порекомендовать единственный способ, а именно, быть крайне аккуратным при прикосновении к раковинам неизвестных моллюсков. Брать их необходимо очень осторожно, избегая мягких тканей животного.

История развития геометрии Интересные факты. История развития геометрии

Самые первые понятия в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков. Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».

Греческие ученые на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.

Однако в труде Евклида ничего не сказано ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру (хотя присутствует теорема о площади круга). История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду, который смог вычислит число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость.

Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний во II веке до нашей эры сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.

Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Однако в дальнейшем история развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.

Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.

Источник: https://interesnyefakty.com/novosti/interesnye-fakty-geometriya-interesnye-fakty-o-geometrii

Интересные факты геометрия. Интересные факты о геометрии

Интересные факты геометрия. Интересные факты о геометрии

1. Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
2. Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
3. С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
4. Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
5. Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
6. Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
7. В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
8. Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
9. Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
10. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
11. Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
12. Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
13. Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
14. При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
15. Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

История развития геометрии Интересные факты. «Школьная газета » Интересные факты о геометрии»

Интересные факты о геометрии.Слово «трапеция» произошло от древнегреческого слова «трапезион»(обозначает столик). также от данного слова произошли уже немногоподзабытые в обиходе слова, такие как «трапеза» и прочие родственныеему слова.Математика для древних греков была, прежде всего, геометрией.Поэтому над двери Академии, в стенах которой Платон учил своих учеников, висела надпись: «Пусть сюда не входит тот, кто не знает геометрии».Греческое слово «конос», обозначающее сосновую шишку, является словарной основой для такого термина как «конус», а известный в геометрии термин «линия» возник уже от латинского слова «линум» (что в переводе на русский язык означает «льняная нить»).Пирог разрезается всего тремя касаниями ножа на восемь равных долей. Причем, существует только два способа это сделать. Под треугольником Рёло понимают геометрическую фигуру, образованную пересечением 3 кругов одинакового радиуса D с центрами, находящимися в вершинах равностороннего треугольника, такой же по длине стороны. на основе треугольника Рёло было придумано сверло, позволяющее просверливатьпочти квадратные отверстия. В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180. В геометрии Римана сумма углов треугольника всегда больше 180.Если число 111 111 111 помножить на себя самого, то получится интересное число 12 345 678 987 654 321 (все числа сначала возрастают, а потом убывают по порядку).Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.Еще факты Знаете ли вы? Что Шарль Перро, автор «Красной Шапочки», написал сказку «Любовь циркуля и линейки»?   Что Наполеон Бонапарт писал математические труды и один геометрический факт называется «Задача Наполеона»?   Что Пифагор был победителем из кулачного боя на 58-х Олимпийских играх, проходивших в 548 году до н. э., а затем побеждал еще на нескольких Олимпиадах? Выполнил Меркулов Лев,Педагог Меркулова О.Р.

Интересные факты о конусе. Конусы

Брюхоногие моллюски рода конус обладают раковиной, длина которой 15 20 см, а форма напоминает коническую. Раковины этих животных окрашены в красивые тона и имеют на поверхности изысканный узор, чем и привлекают коллекционеров, стремящихся заполучить такую раковину. Эти раковины привлекают внимание и охотников за моллюсками, так как на рынках они высоко ценятся туристами.

K наиболее распространенным и брюхоногих моллюсков рода конус относятся:

• , живущие в зоне от Полинезии до Индийского океана;
• , обитающий в зоне Полинезии, и вплоть, до восточного побережья Африки;
• обитающие в регионе от Красного моря до Полинезии;
• — житель берегов Австралии и восточного побережья Африки.

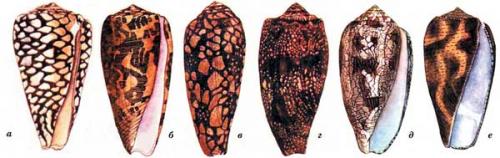
Ловцы конусов могут получить уколы от этих животных, когда они складывают моллюсков в сетчатые мешки, а также могут пострадать и при неосторожной транспортировке мешка, который они, как правило, привязывают к поясу. Сказанное относится к ловцам-профессионалам. Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.

Готовясь напасть , моллюск выдвигает зубы в переднюю часть головы, чтобы вонзить их в тело жертвы. К зубам подходит яд из канала радулы и глотки. В хоботке расположен один из зубов радулы. При уколе пузырек сжимается и яд под давлением вгоняется в свернутые, похожие на острый полый гарпун — зубы радулы.

Конусы обычно предпочитают держаться или свободно . Тропические виды этих моллюсков представляют реальную угрозу для человека, так как их яд, попавший в организм, часто вызывает гибель пострадавших. Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.

Б. Холстед считает, что при развивающихся симптомах отравления ядом расстройства дыхания обычно не бывает, а В. Н. Орлова и Д. Б. Гелашвили указывают, что в тяжелых случаях человек погибает не от остановки сердца, а от паралича дыхательной мускулатуры.

Для предупреждения поражений этими моллюсками можно порекомендовать единственный способ, а именно, быть крайне аккуратным при прикосновении к раковинам неизвестных моллюсков. Брать их необходимо очень осторожно, избегая мягких тканей животного.

Интересные факты о углах. 10 интересных фактов о математике, которые удивляют

Человек может и не быть математиком. 

Более того, он может даже не знать эту науку на минимальном уровне, но тяжело отрицать – математику человек видит практически везде. 

Цифры, фигуры и математические законы преследуют человека повсюду, поэтому нелишним будет узнать кое-что об этой науке.

1. Абрахам де Муавр (математик из Англии) в своей глубокой старости вдруг понял, что его сон увеличивается на 15 минут в каждый последующий день. После этого он составил прогрессию и определил тот день, когда сон займет весь день. Случилось это 27 ноября в 1754 году, и это был день его смерти.

2. Религиозные и верующие евреи стараются всеми силами избегать любых знаков, которые связаны с крестом или символику Христа. К примеру, вместо плюса в школах используют перевернутую «Т».

3. Подлинность денежной купюры евро всегда можно узнать по ее серийному номеру – это буква и 11 цифр. Необходимо поменять букву на то число, которое является порядковым номером этой буквы в алфавите. После этого необходимо сложить все числа и складывать результаты до тех пор, пока не будет одна цифра. И если в итоге получится 8, это говорит о подлинности купюры. Другой способ – сложение всех цифр, без буквы. Итоговый результат, состоящий их буквы и цифры, должен подходить под ту страну, на территории которой появилась купюра. К примеру, Германия – это Х2.

4. Есть версия, что Альфред Нобель отказался включать математику в длинный список наук для своей премии по личным причинам – жена Альфреда спала с математиком. Но в действительности Нобель был холостым. Нет достоверных доказательств того, почему математику не включили, однако есть предположения. К примеру, уже тогда существовала своя премия, но созданная шведским королем. Другая версия – математика является чисто теоретическим предметом, поэтому математики не способны сделать ничего действительно важного для людей и человечества в целом.

5. Есть такая фигура, как треугольник Рело. Она образовывается через пересечение трех идентичных по радиусу кругов, причем центры этих кругов расположены в вершинах треугольника с равными сторонами. Сверло, созданное на основе этого треугольника, дает возможность сверлить только квадратные отверстия. При этом стоит помнить, что сверление таких отверстий с использованием треугольника Рело может иметь погрешность в 2 процента.

6. В русской литература и математике 0 не относится к спискам натуральных чисел, однако на западе 0 является одним из представителей множества таких чисел.

7. Джордж Данциг, математик из Америки, будучи всего лишь университетским аспирантом, один раз опоздал на занятие и, увидев несколько уравнений и подумал о том, что эти уравнения являются общими домашними задачами, которые необходимо выполнить. Это задание показалось ему намного сложнее того, что давали обычно, но он их выполнил и принес результаты преподавателю. И только после этого он узнал, что смог решить 2 нерешаемых уравнения статистики. Причем это были те задачи, которые не могли решить ученые в течение нескольких лет.

8. Если сложить все числа в рулетке, получится 666.

9. Небезызвестная Софья Ковалевская познакомилась с этой наукой о числах в далеком детстве – в ее комнате не было обоев, были лишь лекции ученого Остроградского об исчислениях.

10. В Индиане (штат США) в 1897-ом году выпустили билль, согласно которому число Пи будет равно 3,2. Однако билль не превратился в закон благодаря тому, что в этот процесс вовремя вмешался университетский профессор.

Интересные факты о стереометрии. Изображение пространственных объектов

В планиметрии мы изучали свойства плоских фигур. Хотя в природе их не найдешь – любой объект объёмный. Почему же мы так много времени уделили плоским фигурам, которых не существует в окружающем мире?

Есть природа, а есть модели природных объектов, которые у нас получается исследовать – отрезки, углы, фигуры. Они, в свою очередь, являются элементами объёмных тел. Изучив подробно свойства плоских фигур, теперь мы сможем применять полученные знания для исследования тел в пространстве.

Кирпич имеет форму параллелепипеда, а его грани – форму прямоугольника. Бревно имеет форму цилиндра, а спил (сечение) – форму круга, если спил сделан перпендикулярно оси бревна, и эллипса, если под углом.

То есть переход от планиметрии к стереометрии – это расширение математической модели, а не замена одной на другую.

В планиметрии с изображением фигур было все просто: лист бумаги, по сути, представлял плоскость, и изобразить на нём плоскую фигуру (например, квадрат со стороной а) не составляло труда.

В стереометрии мы будем объёмные фигуры изображать на плоскости, что потребует от нас определенных навыков.

Особенности нашего зрения

Мы привыкли доверять своим глазам и не задаемся вопросом, почему один и тот же объект вблизи выглядит крупнее, чем вдали? Или почему разные по величине предметы порой кажутся одного размера? Механизмы зрения довольно сложны, однако некоторые его особенности можно объяснить на основе геометрических представлений.

Всякий предмет имеет линейные размеры: длину, ширину и высоту. Но как только он попадает в наше поле зрения, то приобретает еще один размер – угловой. Давайте разберемся, что это означает. Когда мы смотрим на предмет, то через каждую его точку можно провести от глаза луч, называемый лучом зрения. Понятно, что их будет бесконечно много. Любые два луча зрения образуют угол зрения (см. рис. 1).

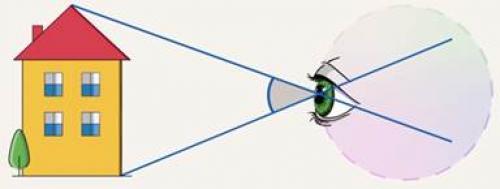
Рис. 1. Угол зрения

Тот угол зрения, под которым предмет виден целиком, и принято называть угловым размером предмета. Как и всякий плоский угол, он измеряется в градусах, минутах, секундах или в радианах.

Угловой размер предмета – величина не постоянная и зависит от расстояния предмета от глаза: чем предмет дальше, тем меньше угол зрения, под которым он виден.

Чтобы понять причину этого явления, вспомним, что на сетчатке глаза изображение предмета получается обратным и уменьшенным. При удалении предмета его изображение на сетчатке становится меньше, поэтому он и кажется нам уменьшающимся (см. рис. 2). При сокращении расстояния изображение, напротив, увеличивается, и предмет кажется увеличивающимся (см. рис. 3).

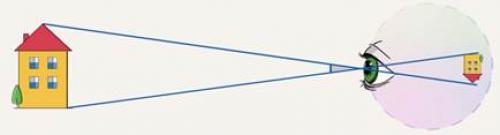
Рис. 2. Предмет кажется уменьшающимся при его удалении

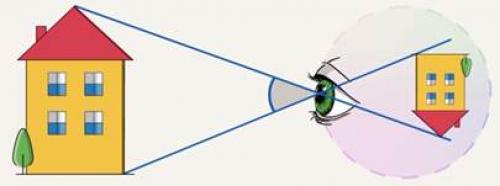
Рис. 3. Предмет кажется увеличивающимся при его приближении

Теперь легко объяснить, почему две «убегающие» вдаль параллельные линии (железнодорожные рельсы, края прямолинейного шоссе) кажутся «сходящимися» в одной точке (см. рис. 4). Такое же впечатление создают ряды телеграфных столбов или деревьев вдоль дороги. Это лишь иллюзия, которая возникает из-за видимого уменьшения расстояния между прямыми по мере их удаления.

Рис. 4. Железнодорожные рельсы кажутся «сходящимися» в одной точке

Часто приходится сталкиваться и с другой ситуацией. Если рассматривать предметы одинаковой формы, но разных линейных размеров под одним и тем же углом зрения, то кажется, что их размеры равны. Поэтому мы можем закрыть монеткой Луну или Солнце.

А при полном солнечном затмении лунный диск в точности заслоняет солнечный (см. рис. 5). В этот момент наблюдатель с Земли видит оба небесных тела под одним углом зрения.

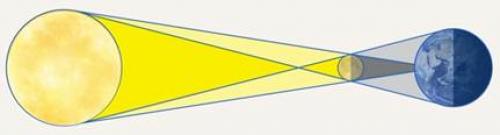
Рис. 5. При полном солнечном затмении лунный диск в точности заслоняет солнечный

Увидеть такое уникальное явление было бы невозможно, если бы линейные размеры Солнца и Луны, а также расстояния от них до Земли не состояли в определенной математической зависимости: диаметры Солнца и Луны (и) и расстояния от этих тел до Земли (и) связаны пропорцией:

Исходя из указанных особенностей нашего зрения, важно научиться правильно изображать объекты, чтобы избежать оптического обмана и искажения восприятия.

Работая с такими фигурами, необходимо научиться изображать их на бумаге. Для этого нужно следовать двум соображениям:

1. При изображении дли́ны отрезков и величи́ны углов могут меняться, т.е. длинный отрезок вполне может быть изображен коротким, а прямой угол острым или тупым;
2. Параллельность отрезков сохраняется всегда. Длины параллельных отрезков меняются в одинаковой степени, т.е. параллельные равные отрезки всегда будут изображены тоже как параллельные и равные.

Пока мы будем использовать эти утверждения без доказательства, так как у нас не хватает теоретической базы. Но скоро мы сможем это сделать. А пока потренируемся изображать различные тела.

Интересное в геометрии. Интересные факты о геометрии

Интересное в геометрии. Интересные факты о геометрии

1. Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
2. Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
3. С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
4. Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
5. Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
6. Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
7. В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
8. Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
9. Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
10. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
11. Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
12. Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
13. Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
14. При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
15. Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

Интересные факты о углах. Интересные факты об угле

Человек применяет уголь в качестве горючего с старейших времен. С момента изобретения его применяли для самых различных целей. Это было и приготовление еды, и производство.

Благодаря углю стало вероятно изготавливать сталь. С углем связано множество любопытных фактов, а его роль в нашей жизни велика.

Образование угля в недрах почвы – весьма продолжительный процесс. Тут большое количество неспециализированного с нефтью. Уголь образуется из погибших растений, каковые по тем либо иным обстоятельствам выяснялись под почвой. Тут без кислорода они не гнили, и их остатки не теряли находившийся в них углерод – базу угля. Потом в течение миллионов лет под действием самых различных факторов эти остатки преобразовывались в торф, а из него в уголь.

А предстоящий процесс ведет к образованию графита.

Прежде, чем углубляться в интересные факты о разработка интересных ситуаций и добычи, которые связаны с углем, поболтаем об углях, нужных для того чтобы:
По большому счету главное отличие японской кухни от европейской – доминирование морепродуктов. Их применяют везде. А также для шашлыков, каковые японцы именуют «тэмпора». Действительно, наряду с этим они не частенько применяют уголь для их изготовление. Считается, что он способен впитывать запахи и после этого отдавать их подготавливающемуся блюду.

Углю по большей части предпочитают открытый пламя. А в дополнение довольно часто применяют имбирь, что кроме этого ликвидирует запахи.

В Северной Африке во франкоговорящих государствах обожают применять сухой кустарники и другие небольшие растения. Тут пустыня, и больших деревьев нет. Угли делают, к примеру, из саксаула.

Они получаются тёплыми и владеющими своеобразным запахом.

У нас же в Российской Федерации привычнее применять уголь для шашлыка в брикетах. Лично от себя могу дать совет компанию Хороший уголь, которая специализирутеся на производстве угля для кальяна и барбекю наивысшего качества.

Шахты, в которых добывают уголь, являются достаточно страшным местом. В них выделяются разные газы. Очень страшен метан. Он вытесняет часть кислорода совершает воздушное пространство взрывоопасным. Раньше, в то время, когда индикаторов метана не существовало, применяли канареек.

Их забирали в шахту, и в случае если птицам становилось не хорошо, это означало, что в шахте скопился метан.

Среди вторых опасностей выделяются пожары в шахтах. Как в случаях с горящим торфом, они смогут длить достаточно продолжительно. Рекордным оказался пожар на месторождении Люхуангоу в Китае.

На его устранение ушло целых 130 лет, и совсем его потушили лишь в 2004 году. Было стёрто с лица земли около 260 млн. тысячь киллограм угля.

С его месторождениями и углём связано множество забавных обстановок. В нем довольно часто обнаружили сокровища. Так в первой половине 90-ых годов XIX века повезло некой госпоже Калп, отыскавшей в громадном куске угля древнюю золотую цепочку.

Уголь хранит множество древних артефактов. Шахтеры неоднократно обнаружили останки древних сооружений. Как, к примеру, в американском городе Хаммондвилле, где во второй половине 60-ых годов XIX века нашли останки стенки с иероглифами.

Уголь играет громадную роль в жизни людей а также целых городов. Весьма интересно проследить судьбу японского города Хасима, находящегося на одноименном острове, что был некогда богат углем. Начиная с 30-х годов века прошлого, данный город продолжительное время считался самым многолюдным в мире. Остров владел береговой линией всего в 1 км, но его население составляло более 5 тыс. человек.

Но к середине 70-х уголь тут закончился. Люди начали покидать это место. Город стал полностью закинутым.

на данный момент в том месте кроме того выполняют экстремальные экскурсии.

В Российской Федерации находятся огромные запасы угля. Ученые заявляют о 4 триллионах тысячь киллограм запасов. Это чуть менее трети от общемировых.

Уголь может иметь не только привычную жёсткую форму. Сейчас имеются разработке, превращающие его в жидкое горючее, весьма похожее на нефть.

В индустрии уголь применяют не только в качестве горючего. Он есть сырьем для производства разных материалов. К примеру, из каменного угля делают неестественный графит.

И вдобавок из угля добывают содержащиеся в нем нужные материалы: свинец, серу, галлий, цинк и другие.

Интересные факты о трапеции. Презентация 8 класса на тему: «Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина.». Скачать бесплатно и без регистрации. — Транскрипт:

---

1 Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина

2 Цели: 1.Узнать интересную информацию о геометрической фигуре «трапеция»; 2.Показать, что она встречается в нашей жизни чаще, чем нам кажется.

3 То, что мы знаем о трапеции: Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции ее средняя линия параллельна основаниям и равна их полусумме; если трапеция равнобедренная, то ее диагонали равны и углы при основании равны; / 5

4 А вот то, что мы еще не знаем: ее средняя линия равна полусумме оснований; если трапеция равнобедренная, то около нее можно описать окружность; если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

9 Задача 1. Треугольник из трапеций! Сложите из трех одинаковых трапеций равносторонний треугольник. Трапеции нельзя накладывать друг на друга, разрезать. Треугольник должен получиться целый (без отверстий внутри) и без лишних частей снаружи фигуры.

11 Задача 2. Четыре из одной! Разрежьте данную фигуру на четыре равные и одинаковые по форме части, не повторяющие, однако, исходную форму.

13 Итак: С помощью этой презентации вы узнали, как часто встречается трапеция в нашей жизни! Вы решили несколько интересных задач, связанных с трапецией. Мы надеемся, что вам было интересно!

Интересные факты о конусе. Есть много интересных фактов о конусе

Есть много интересных фактов о конусе. Во многих религиях и учениях , конус имеет культовое значение. Имеется множество обрядов ,в которых затрагивается магические свойства конуса , например, у ведьм и колдуний имеется ритуал — «конус силы».

Слайд 22 из презентации «Конус»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Конус.ppt» можно в zip-архиве размером 786 КБ.

Похожие презентации

краткое содержание других презентаций на тему слайда

«Конус и усечённый конус» — Одна из частей представляет собой конус, а другая называется усеченным конусом. Осевое сечение. Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Используя формулу (2), получаем. Усеченный конус. Боковая поверхность. В. Для вычисления площади SКОН полной поверхности конуса получается формула.

«Цилиндр конус шар» — Объём шара радиуса R равен . Определение цилиндра. Объём шара Теорема. Найти объём и площадь поверхности шара. Виды тел вращения. Объём шарового сегмента. Шаровой сегмент. Сечения шара. Сечения цилиндра.  — Шаровые сегменты. Объём шарового сектора. Задача № 3. Сечение конуса. Тела вращения. Завершить работу.

«Конус» — Конус, усеченный конус. Усеченный конус – геометрическое тело, отсеченное от конуса плоскостью, параллельной основанию. Доказательство Пусть b – плоскость перпендикулярная оси конуса и пересекающая конус. Формулы. Теорема. Геометрия. Усеченный конус.

«Урок конус» — Кусты в королевском саду. Объем конуса. Проблемно-поисковый семинар работа в группах. Тема урока: «Конус. Карликовое дерево. Работа в группах 6) 5 мин: Коррекция. Задача №2: Стог сена имеет форму цилиндра с коническим верхом. Вопрос №8: По какой формуле можно вычислить объем цилиндра? Развивающие задачи урока.

«Объём конуса» — 1. Высота конуса равна 8 см. 2. В правильную треугольную пирамиду вписан конус. Объем конуса равен V. Найдите объем пирамиды. Решение задач. 3. В конус вписана правильная треугольная пирамида. Объем конуса.

«Конус геометрия» — Основание. R-радиус основания. Образующие. H-высота. Вершина. Конус. L-образующая. Применение конуса и усеченного конуса в повседневной жизни. Центр основания. С конусом люди знакомы с глубокой древности. Конус в переводе с греческого «konos» означает «сосновая шишка».