Электрическое поле — Википедия

Материал из Википедии — свободной энциклопедии

Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле^[1], существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела^[2].

Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия.

В классической физике система уравнений Максвелла описывает взаимодействие электрического поля, магнитного поля и воздействие зарядов на эту систему полей.

Основным действием электрического поля является силовое воздействие на неподвижные относительно наблюдателя электрически заряженные тела или частицы. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца).

Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле

u=12(E→D→),{\displaystyle u={\frac {1}{2}}\left({\vec {E}}{\vec {D}}\right),}

где E — напряжённость электрического поля, D — индукция электрического поля.

Однородное поле[править | править код]

Направление линий напряжённости между двумя разнозаряженными пластинами

Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства. Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу.

Наблюдение электрического поля в быту[править | править код]

Для того, чтобы создать электрическое поле, необходимо создать электрический заряд. Натрите какой-нибудь диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные чистые волосы. На ручке создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, например, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие электрических разрядов.

Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с ЭЛТ) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице.

Электрическое поле внутри проводников с избыточными зарядами[править | править код]

Из опытов, приводимых в электростатике, известно, что избыточные заряды привнесённые в проводник извне, перемещаются к поверхности проводника и остаются у поверхности проводника. Само перемещение избыточных зарядов к поверхности проводника свидетельствует о наличии электрического поля внутри проводника в период перемещения к поверхности проводника.

Электрическое поле внутри проводников с недостатком собственных электронов[править | править код]

При недостатке собственных электронов тело получает положительный заряд «дырочной» природы. Дырки при этом ведут себя подобно электронам и также распределяются по поверхности тела.

Расчёты электрического поля можно проводить аналитическими^[3][4][5]

или численными методами^[6]. Аналитические методы удается применить лишь в простейших случаях, на практике в основном используются численные методы. Численные методы включают в себя: метод сеток или метод конечных разностей; вариационные методы; метод конечных элементов; метод интегральных уравнений; метод эквивалентных зарядов^[6].

• Орир, Джей — Популярная физика: [пер. с англ.].: Мир, 1966. — 446 с.
• Учебник «Элементарный учебник физики» под ред. Ландсберга Г. С., Часть 2 (Электричество и магнетизм.)
• Трофимова Т. И. Курс физики: Учеб. пособие для вузов.—2-е изд., перераб. и доп.— М.: Высш. шк., 1990.—478 с.: ил. ISBN 5-06-001540-8

1.8. Электромагнитная индукция. Взаимосвязь электрических и магнитных полей.

Электрические и магнитные поля порождаются одними и теми же источниками — электрическими зарядами. Поэтому можно было предположить, что между этими полями существует определенная связь. Это предположение нашло экспериментальное подтверждение.

Когда в 1820 г. Эрстед впервые обнаружил, что магнетизм может быть получен электрическим током, вдохновлённый новизнойидеи Майкл Фарадей задумался об обратном процессе — превращении магнетизма в электрический ток. Поставленную задачу превращения магнетизма в электричество Фарадей зафиксировал в своем дневнике в 1821 г. С тех пор он, не переставая, думал об этом.

Как часто бывает в истории науки, новые идеи приходят не только к одному ученому. Так было и с идеей получения электричества с помощью магнетизма. Практически одновременно над проблемой бились Фарадей и другие ученые. Швейцарский физик Жан-Даниэль Колладон (1802-1893 гг.) также пытался получить электрический ток с помощью магнита. При работе он пользовался гальванометром. Чтобы магнит не оказывал непосредственного влияния на стрелку гальванометра, концы катушки, в которую Колладон вдвигал магнит, надеясь получить в ней ток, были выведены в соседнюю комнату. Вдвинув магнит в катушку, Колладон направлялся в комнату, где находился гальванометр, и с огорчением отмечал, что стрелка гальванометра стояла на нуле, т.е. ток в катушке не возникал. Стоило ему все время наблюдать за гальванометром или попросить кого-либо заняться магнитом, замечательное открытие было бы сделано Колладоном. Но этого не случилось. Покоящийся относительно катушки магнит мог лежать преспокойно внутри нее сколь угодно долго, не вызывая в катушке тока.

! Лишь движущийся магнит, создающий изменяющееся магнитное поле, является причиной появления электрического тока.

Вто же время за океаном другой ученый — американецДжозеф Генри (1799-1878 гг.), родившийся, как и Фарадей, в бедной семье и также вынужденный заниматься самообразованием, экспериментальным путем пришел к открытию нового явления. Случилось это за год до открытия Фарадея, но в силу жизненных обстоятельств результатов своих Генри не опубликовал.

29 августа 1831 г., ничего не зная об открытии Генри, Фарадей фиксирует появление индукционного тока в замкнутом проводнике, помещенном в переменное магнитное поле. Данное явление Фарадей назвал индукцией тока. (По-русски слово «индукция» означает наведение). Первоначально была открыта индукция неподвижных друг относительно друга токов.

!В замкнутом контуре возникает индукционный ток при изменении числа силовых линий магнитного поля, пронизывающих площадь, ограниченную этим контуром.

!Чем быстрее меняется число линий магнитного поля, тем больше электрический ток.

Причина изменения силовых линий безразлична: это может быть и изменение силы тока, и сближение катушек, и движение магнита.

Возникающий индукционный ток немедленно начинает взаимодействовать с породившим его током или магнитом. Направление индукционного тока определяется с помощью правила Ленца:

Возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которым вызывается данный ток.

Истинный смысл электромагнитной индукции был найден Дж. Максвеллом (1831-1879 гг.). Максвелл развил идеи М. Фарадея, создал теорию электромагнитного поля. Основная часть теории — это уравнения, описывающие законы электромагнетизма, так называемые уравнения Максвелла. Их изучение не входит в рамки нашего курса, следует только заметить, что известные нам законы — Кулона, Ампера являются частными случаями этих уравнений. Уравнения имеют лаконичную форму, на языке высшей математики описывают поведение электрических и магнитных полей. Одно из уравнений имеет такой смысл: изменяясь во времени

, переменное магнитное поле порождает вокруг себя электрическое.

Согласно теории Максвелла: переменное магнитное поле порождает переменное электрическое поле; переменное электрическое поле порождает переменное магнитное.

Переменное электрическое и переменное магнитные поля — это две составляющие единого электромагнитного поля. Распространяется электромагнитное поле в пространстве в виде электромагнитных волн со скоростью, равной скорости света в вакууме (3 • 10⁸м/с).

!Источником электромагнитных волн являются электрические заряды, движущиеся с ускорением.

При ускоренном движениивозникающее электромагнитное поле «отрывается» от частицы и начинает существовать самостоятельно в виде электромагнитных волн. Электромагнитные волны могут распространяться не только в среде, но и в вакууме. Векторы напря­

женности электрического поля и магнитной индукции в электромагнитной волне перпендикулярны друг другу и вектору скорости распространения волны (рис. 9).

Первоначально существование электромагнитных волн было предсказано теоретически. Примерно через полтора десятка лет немецкий физикГ. Герц (1857-1894 гг.) экспериментально доказал существование электромагнитных волн. Началось изучение свойств электромагнитных волн. Ещё через десяток лет нашлись первые пути их практического применения: была осуществлена беспроводная радиосвязь.

Glava_18_Teoria_Maxvella

Глава 18. Связь электрического и магнитного полей.

Электромагнитные волны.

§ 18.1

Теория Максвелла. Ток смещения. Уравнения Максвелла

Анализируя связь между величинами электрического и магнитного поля и обобщая результаты опытов Эрстеда и Фарадея, Максвелл создал теорию электромагнитного поля. Теория Максвелла с единой точки зре­ния позволяет объяснять свойства электрических и магнитных полей. Основные закономерности электромагнитных явлений описываются уравнениями Максвелла, и они составляют основу как электротехники и радиотехники, так и теории любых электромагнитных явлений.

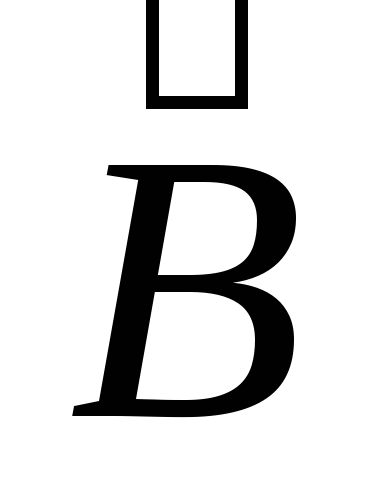В каждой точке пространства и в каждый момент времени состояние электромагнитного поля характеризуется двумя векторами – вектором напряжённости электрического поля и вектором магнитного поля -магнитной индукцией . Вектора и являются силовыми характеристиками электромагнитного поля, т.е. такими характеристиками, от которых зависит сила, действующая со стороны этого поля на любую находящуюся в нём заряженную частицу.

Электромагнитное поле по разному действует на заряженную частицу в том случае, когда эта частица покоится, и в том случае, когда она движется.

Сила, с которой электромагнитное поле действует на покоящийся в данной системе отсчёта заряд, называется электрической силой:

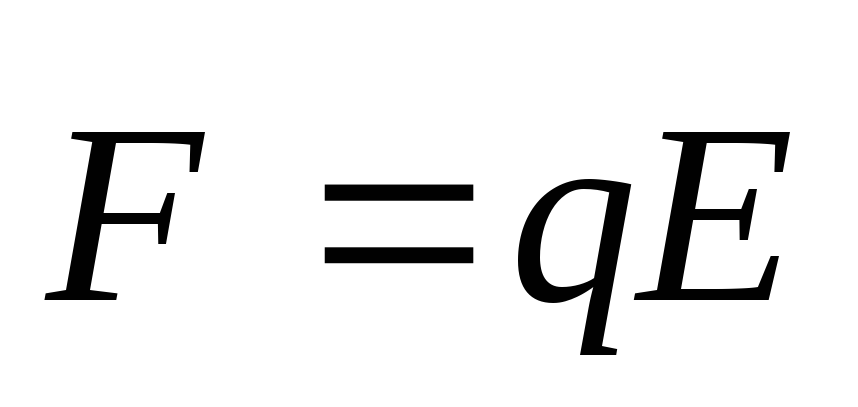
Сила, действующая в электромагнитном поле на движущийся заряд и дополнительная к электрической силе, называется магнитной силой или силой Лоренца:

В 1892 г. Лоренц получает формулу силы, с которой электромагнитное поле действует на любую находящуюся в нём заряженную частицу:

(18.1)

Эта сила называется электромагнитной силой Лоренца, а данное выражение является одним из основных законов классической электродинамики.

В теории решена основная задача электродинамики — по заданному распределению зарядов и токов определяются характеристики создавае­мых ими электрических и магнитных полей. Уравнения Максвелла учитывают среду феноменологически, т. е. не раскрывают механизма взаимодействия среды и поля. Среда описывается с помощью трех величин: диэлектрической проницаемостью ε, магнитной проницаемостью μ и удельной электрической проводимостью γ.

Теория Максвелла – теория близкодействия, согласно которой электрические и магнитные взаимодействия распространяются с конечной скоростью, равной скорости света в данной среде.

В основе теории Максвелла лежат два положения.

1. Всякое переменное электрическое поле порождает вихревое магнитное.

2. Всякое переменное магнитное поле порождает вихревое электрическое.

При изучении явления электромагнитной индукции было показано, что переменное магнитное поле порождает вихревое электрическое поле, которое не связано с зарядами, как в случае электростатиче­ского поля; его силовые линии не начинаются и не заканчиваются на за­рядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля.

Сущность явления электромагнитной индукции заключается не столько в появле­нии индуцированного тока, сколько в возникновении вихревого электрического поля. Это фундаментальное положение электродинамики установлено Максвеллом как обобщение закона электромагнитной индукции Фарадея.

Направление вектора напряженности вихревого электрического поля устанавливается в соответствии с законом электромагнитной индукции Фарадея и правилом Ленца:

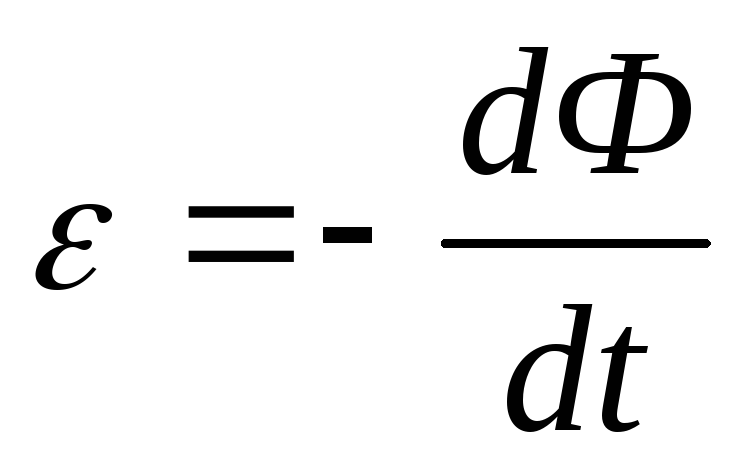
Согласно определению электродвижущей силы

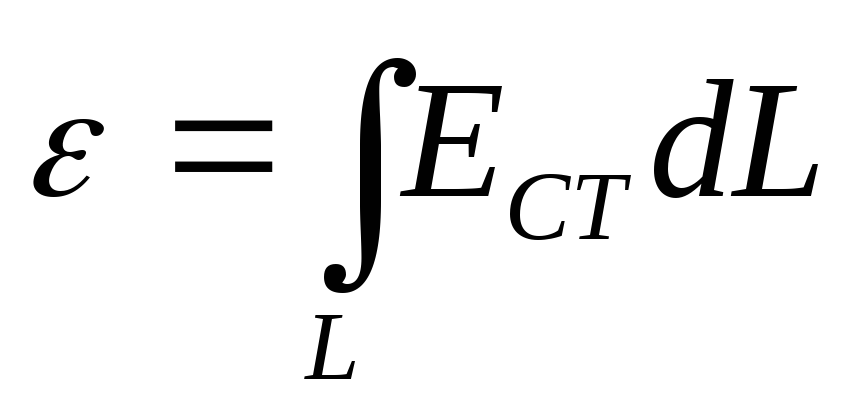
E_СТ -напряжённость поля сторонних сил.

В явлении электромагнитной индукции этой величиной является напряжённость вихревого электрического поля, поэтому

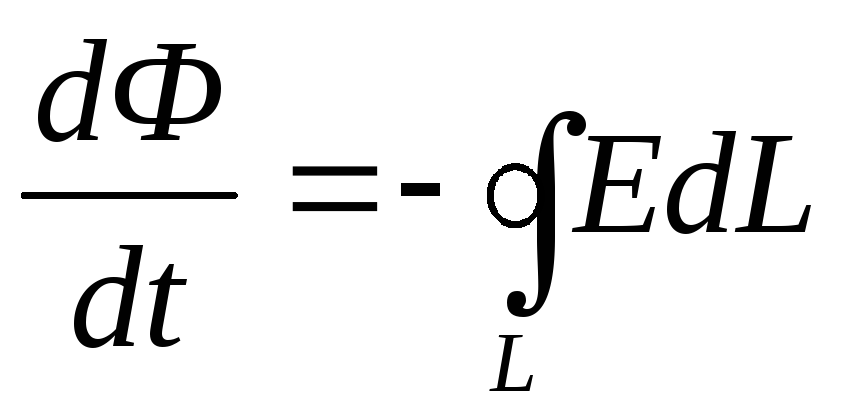(18.2)

Уравнение (18.2) выражает количественную связь между изменяю­щимся магнитным полем В и вихревым электрическим полем Е:

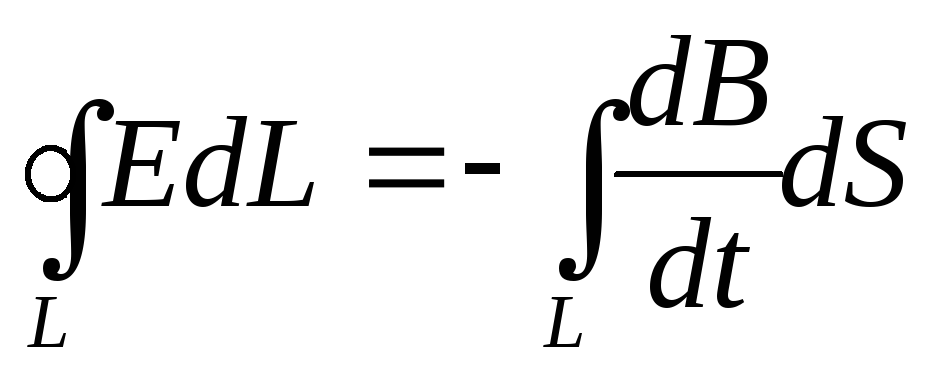(18.3)

Циркуляция вектора напряженности электрического поля по любому замкнутому контуру пропорциональна скорости приращения магнитного потока сквозь любую поверхность, ограниченную данным контуром.

При этом циркуляция электрического поля и скорость приращения магнитного потока имеют противоположные знаки.

Формула (18.3) выражает первое уравнение Максвелла в интегральной форме.

При рассмотрении постоянного и переменного токов в проводнике имеют место физические эффекты, которые, как правило, отличаются друг от друга. Например, когда по проводнику проходит постоянный ток, то линии тока всегда замкнуты. Обратимся к процессу прохождения переменного тока по цепи, содержащей конденсатор. Между пластинами конденсатора заряды не могут перемещаться. Это приводит к тому, что линии тока обрываются у поверхности пласти­ны конденсатора, в результате чего ток проводимости, текущий по проводнику, соединяющему обкладки конденсатора, оказывается разомкнутым. До сих пор мы исходили из представления, что электрические токи представляют собой движение электрических зарядов по проводникам и что плотность их определяется электропроводимостью проводника. В плоском конденсаторе одна из обкладок его имеет положительный заряд с поверхностной плотностью +σ, другая — отрицательный с поверхностной плотностью — σ (рис.18.1). При разряде конденсатора через проводник, соединяющий обкладки, ток течет от обкладки М к N.

Плотность тока j внутри обкладки конденсатора определяется производной по времени от плотности электрического заряда:

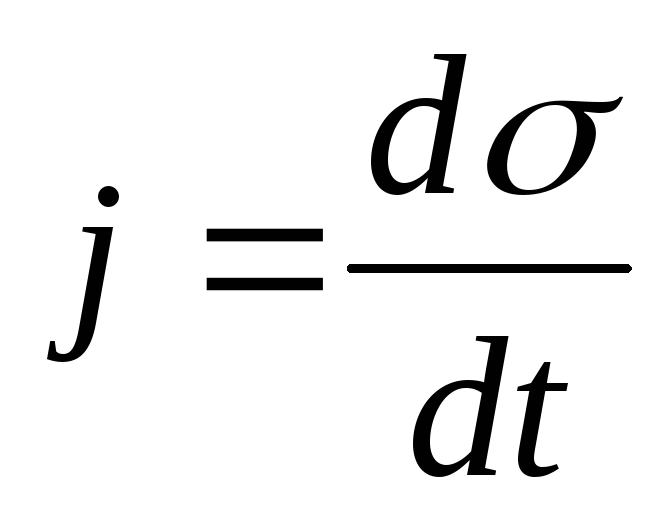(18.4)

Ток такой плотности течет от обкладки М конденсатора.

Обратимся теперь к тому, что происходит в это время между обкладками конденсатора. Как известно, электрическое смещение поля связано с напряженностью соотношением

D=εε₀Е (18.5)

а напряженность поля внутри конденсатора равна

(18.6)

Объединяя формулы (18.5), (18.6), получаем, что электрическая индукция между обкладками конденсатора равна

D= σ (18.7)

При разряде конденсатора изменяется со временем поверхностная плотность σ заряда пластин конденсатора; следовательно, в соответствии с формулой (18.7) изменяется и электрическая индукция D:

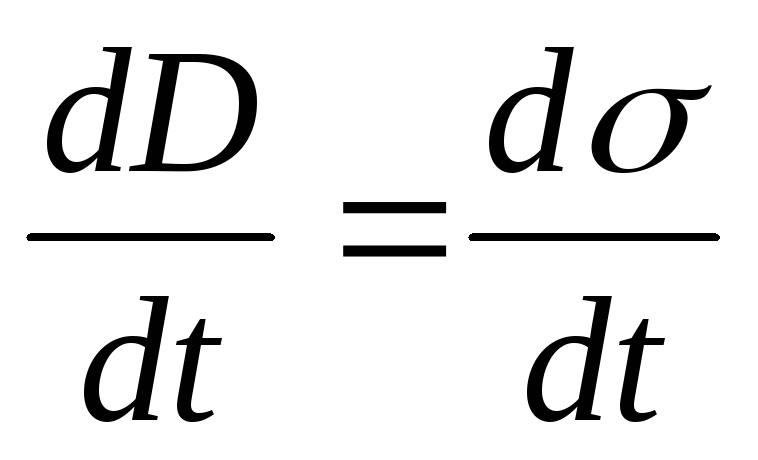(18.8)

Так как вектор электрического смещения поля направлен от положительно заряженной пластины N к отрицательно заряженной пластине М, то при разряде конденсатора скорость изменения электрической индукции отрицательна и направлена в сторону, противоположную вектору D. Из сказанного следует, что направление вектора 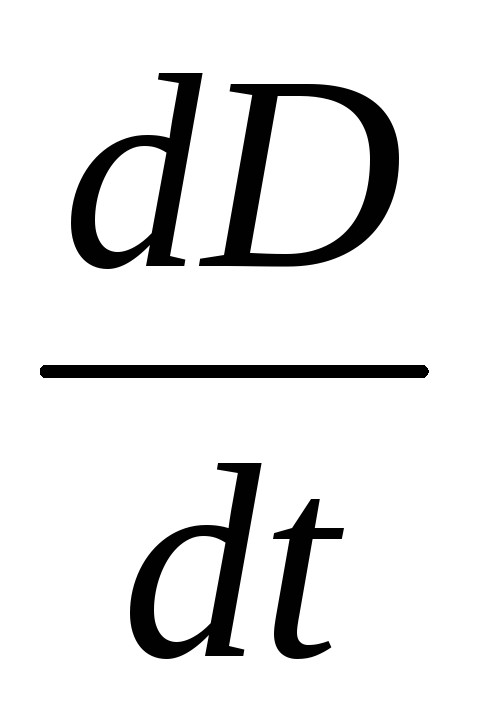совпадает с направлением тока в цепи, в которую включен конденсатор. Как видно из уравнений (18.4) и (18.8), плотность электрического тока j и величина равны между собой.

Максвелл назвал величину 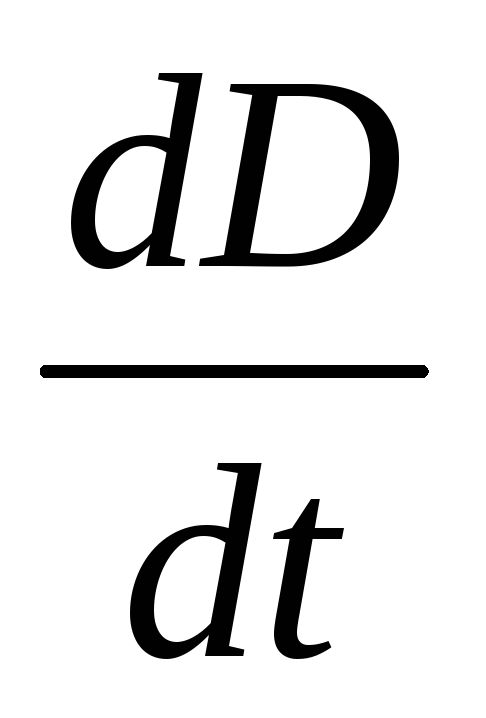плотностью тока смещения:

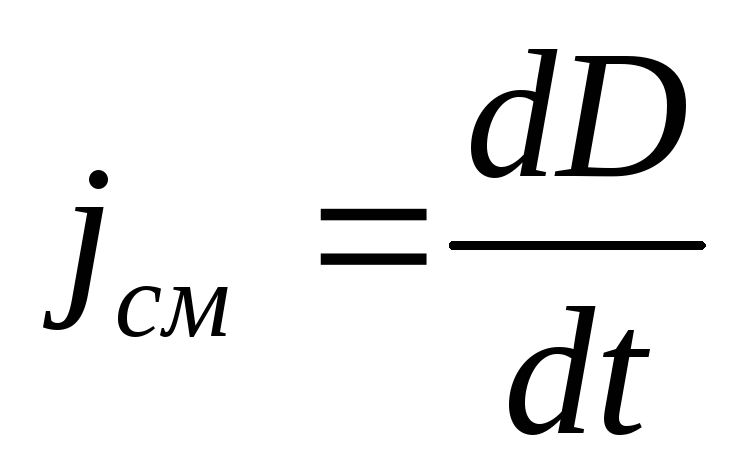(18.9)

Таким образом, ток смещения — это скорость изменения электрического смещения, определяемого по формуле

D=ε₀Е+P

[Е — напряженность электрического поля, Р — поляризованность].

Плотность тока смещения

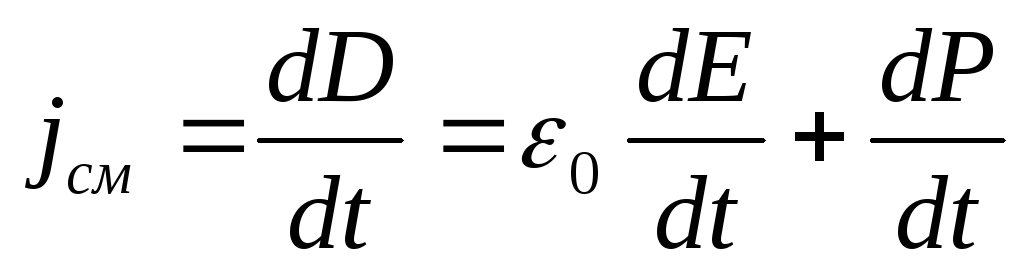(18.10)

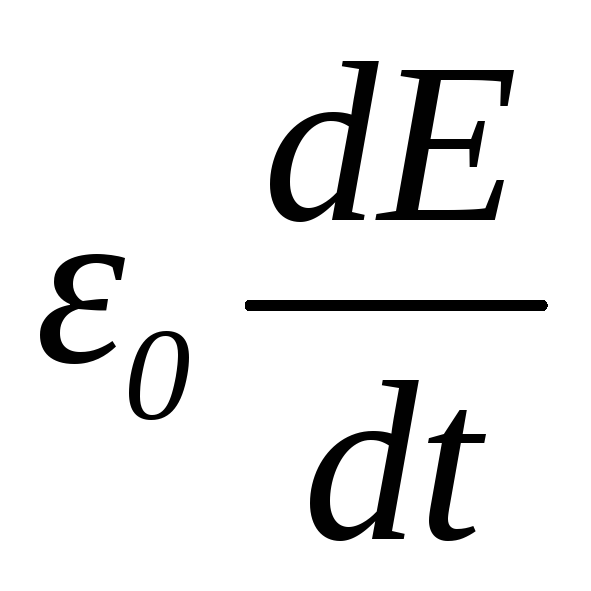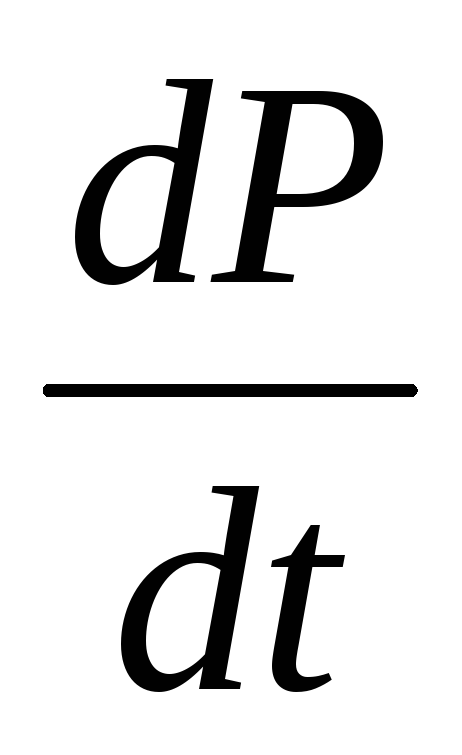[— плотность тока смещения в вакууме: — плотность тока поляризации, т. е. упорядоченного движения электрических зарядов в диэлектрике].

Так как числовые значения плотности тока смещения j_см и плотности тока проводимости j равны, то линии плотности тока проводимости внутри проводника (естественно, включая и пластины конденсатора) не­прерывно переходят в линии плотности тока смещения между обкладками конденсатора. Для того чтобы ток был замкнут, вводится понятие полного тока, который включает в себя сумму тока проводимости и тока смещения; т. е. плотность полного тока равна

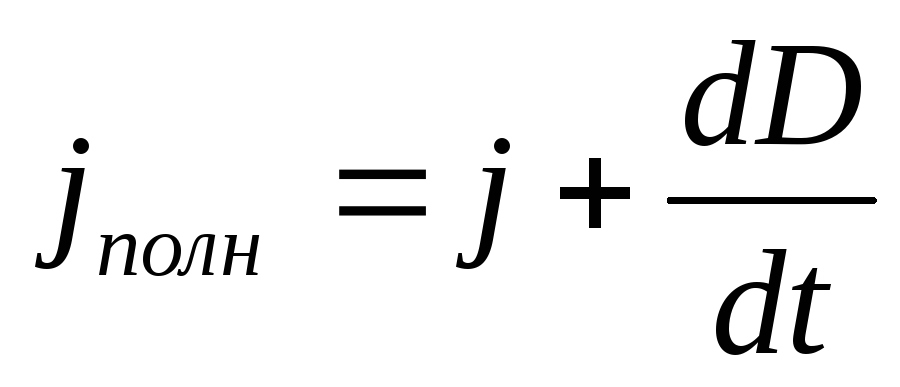(18.11)

Таким образом, ток смещения – переменное электрическое поле; подобно току проводимости, порождает магнитное поле, силовые линии которого всегда замкнуты.

Максвелл, обобщая закон полного тока

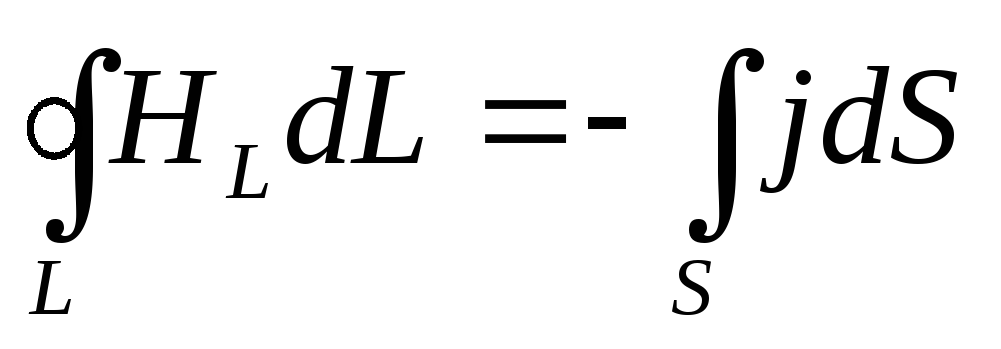(18.12)

и вводя в правую часть тока проводимости также ток смещения, нашёл уравнение

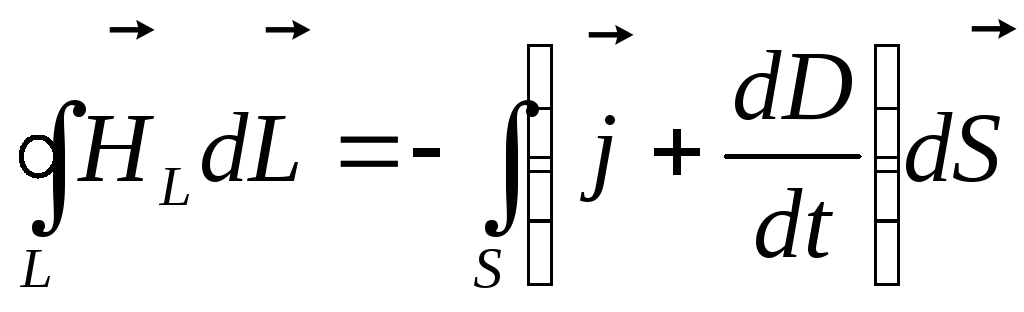(18.13)

Получившее название второго уравнения Максвелла.

В систему уравнений Максвелла кроме двух описанных выше входят теорема Гаусса для электрического и магнитных полей:

При непрерывном распределении заряда внутри замкнутой поверхности с объёмной плотностью выражение имеет вид

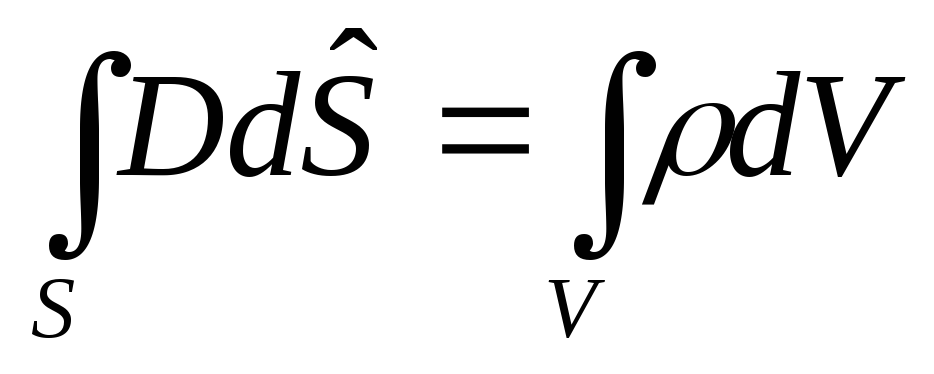
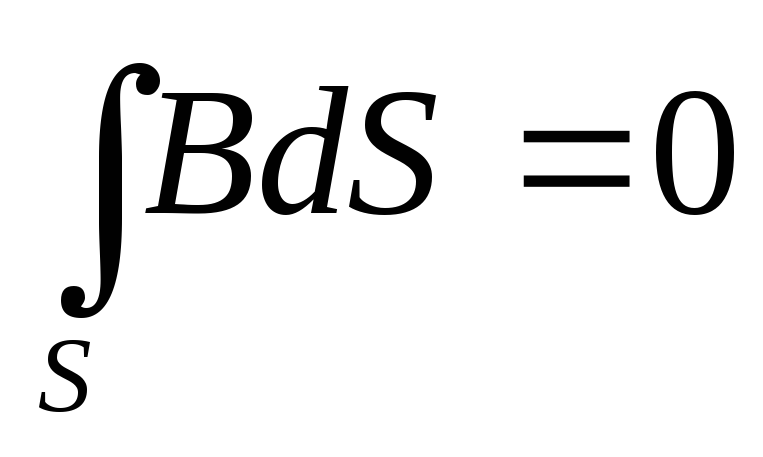
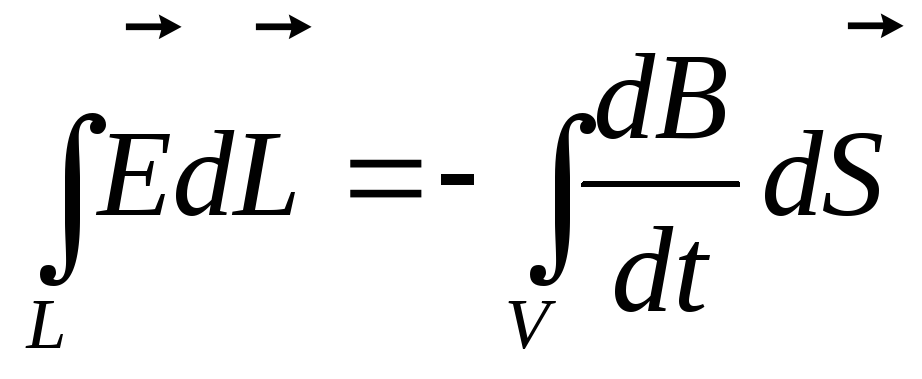
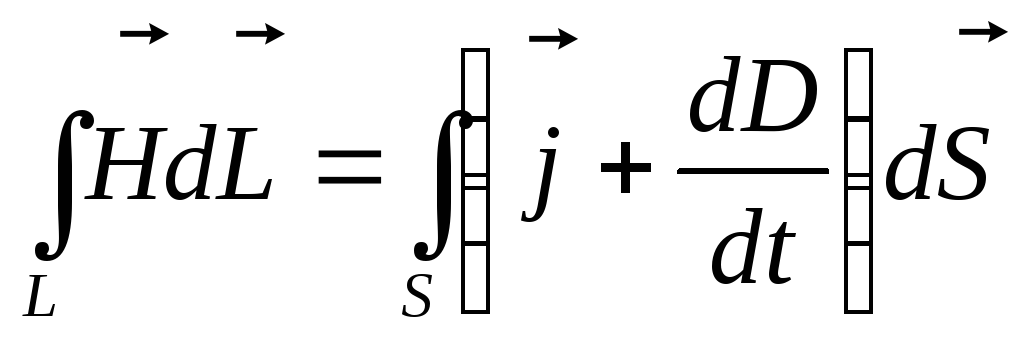
Первые два уравнения свидетельствуют о том, что электрическое поле возникает как вокруг неподвижных зарядов, так и в том случае, когда происходит изменение индукции магнитного поля во времени.

Вторые два уравнения показывают, что магнитное поле является вихревым и возникает лишь при наличии электрических токов или изменяющегося во времени электрического поля или того и другого одновременно, т.е. никаких магнитных зарядов не существует.

Из уравнений Максвелла следует, что электрические и магнитные поля являются проявлением единого электромагнитного поля.

Обычно к системе уравнений максвелла присоединяют формулы, выражающие связь между и , и

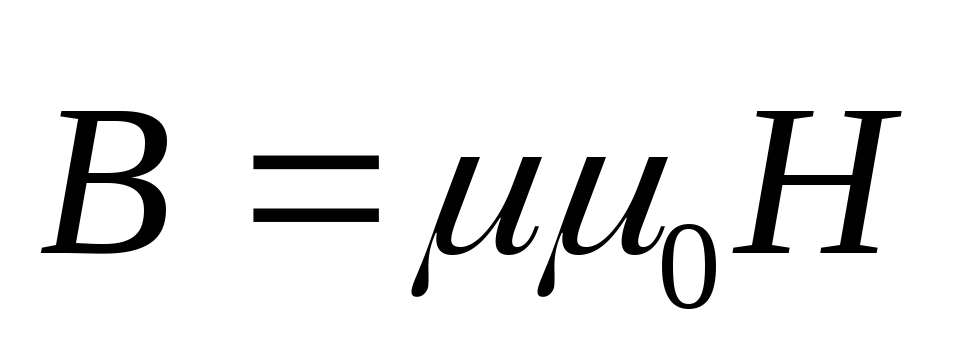
Физический смысл уравнений Максвелла:

1.Электромагнитное поле можно разделить на электрическое и магнитное лишь относительно;

2. Изменяющееся магнитное поле порождает электрическое поле, и изменяющееся электрическое поле порождает магнитное, причём эти поля взаимосвязаны.

Из уравнений Максвелла следует, что электромагнитное поле способно существовать в отсутствии электрических зарядов и токов.

При этом изменение его состояния имеет волновой характер, т.е. является электромагнитной волной. Электромагнитная волна в вакууме распространяется со скоростью света. Теоретические предсказания Максвелла подтвердили опыты Герца и изобретение радио Поповым

§ 18.2 Электромагнитные волны

Гипотеза Максвелла предполагает существование электромагнитной волны, которая представляет собой распространяющиеся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис.18.3).

Электромагнитные волны распространяются в веществе с конечной скоростью

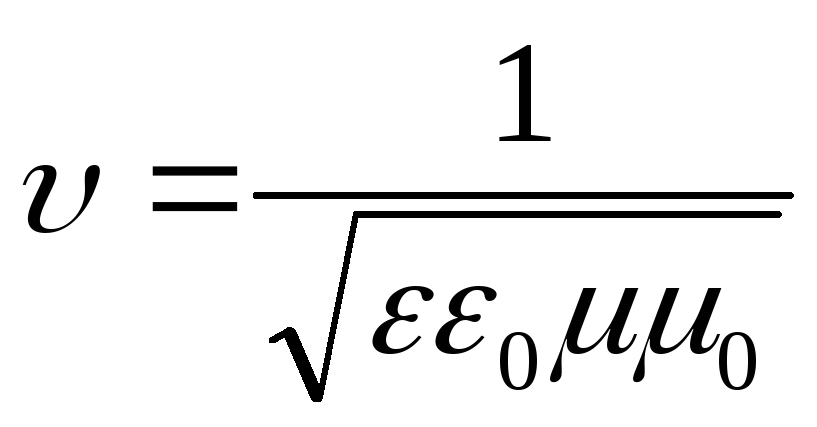(18.14)

где ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м.

Длина волны λ в синусоидальной волне связана со скоростью υ распространения волны соотношением λ = υT 

Скорость электромагнитных волн в вакууме (ε = μ = 1):

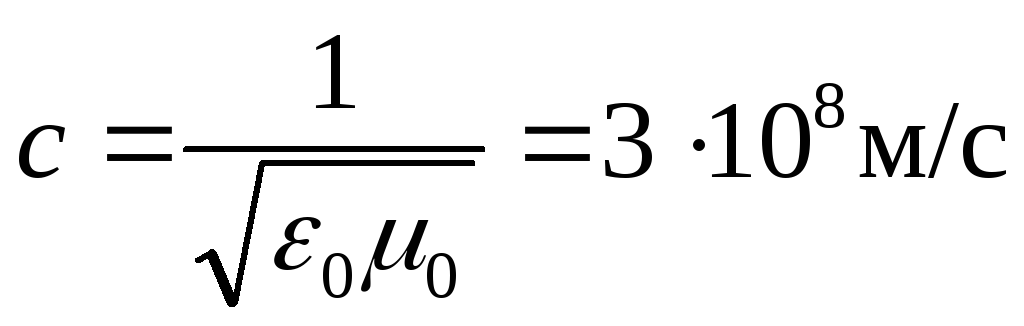(18.15)

Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.

Вывод Максвелла о конечной скорости распространения электромагнитных волн находился в противоречии с принятой в то время теорией дальнодействия, в которой скорость распространения электрического и магнитного полей принималась бесконечно большой. Поэтому теорию Максвелла называют теорией близкодействия.

В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: ω_Э= ω_м

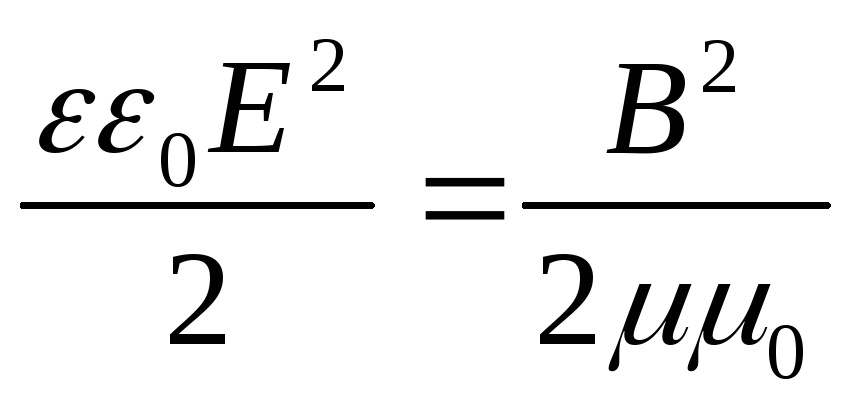(18.16)

Отсюда следует, что в электромагнитной волне модули индукции магнитного поля и напряженности электрического поля в каждой точке пространства связаны соотношением

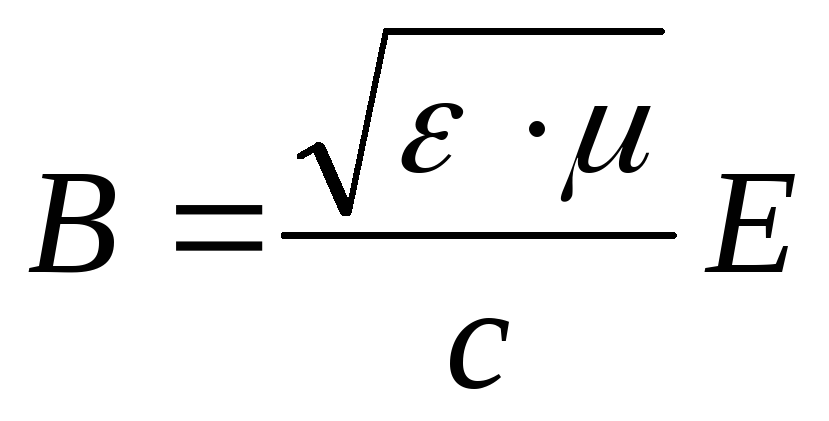(18.17)

Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 2.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔW_эм, равная

ΔWэм = (ωэ + ωм)υSΔt.

Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:

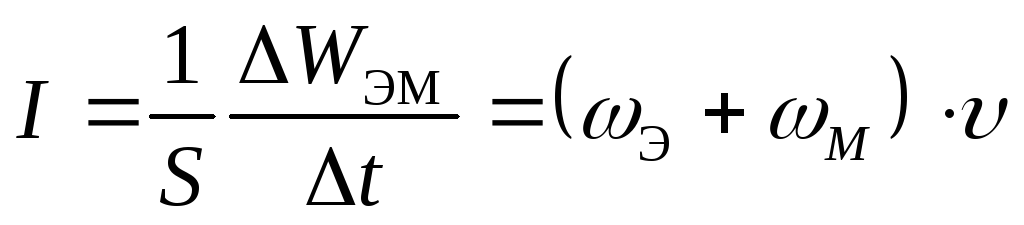
Подставляя сюда выражения для ω_э, ω_м и υ, можно получить:

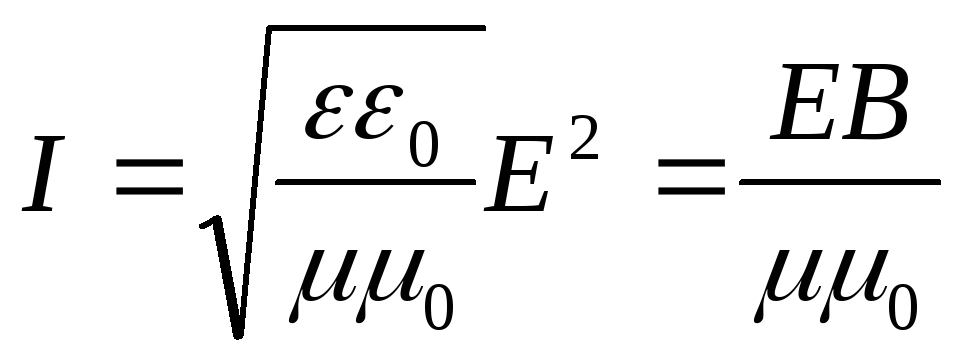(18.18)

Поток энергии в электромагнитной волне можно задавать с помощью вектора , направление которого совпадает с направлением распространения волны, а модуль равен . Этот вектор называют вектором Умова-Пойнтинга.

В синусоидальной (гармонической) волне в вакууме среднее значение I_ср плотности потока электромагнитной энергии равно

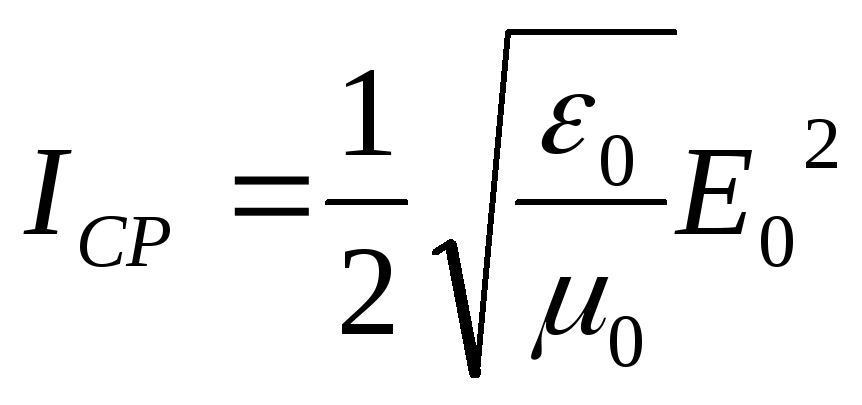(18.19)

где E₀ – амплитуда колебаний напряженности электрического поля.

Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м²).

Из теории Максвелла следует, что электромагнитные волны должны оказывать давление на поглощающее или отражающее тело. Давление электромагнитного излучения объясняется тем, что под действием электрического поля волны в веществе возникают слабые токи, то есть упорядоченное движение заряженных частиц. На эти токи действует сила Ампера со стороны магнитного поля волны, направленная в толщу вещества. Эта сила и создает результирующее давление. Обычно давление электромагнитного излучения ничтожно мало. Так, например, давление солнечного излучения, приходящего на Землю, на абсолютно поглощающую поверхность составляет примерно 5 мкПа. Первые эксперименты по определению давления излучения на отражающие и поглощающие тела, подтвердившие вывод теории Максвелла, были выполнены П. Н. Лебедевым в 1900 г. Опыты Лебедева имели огромное значение для утверждения электромагнитной теории Максвелла.

Существование давления электромагнитных волн позволяет сделать вывод о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля в единичном объеме выражается соотношением

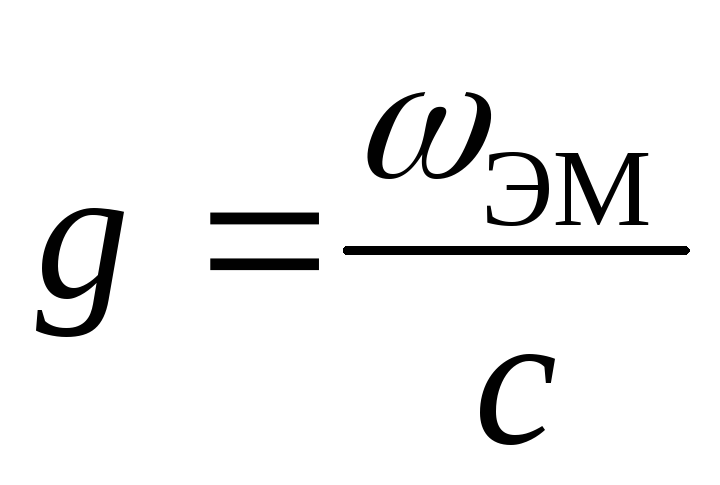
где ω_эм – объемная плотность электромагнитной энергии, c – скорость распространения волн в вакууме. Наличие электромагнитного импульса позволяет ввести понятие электромагнитной массы.

Для поля в единичном объеме

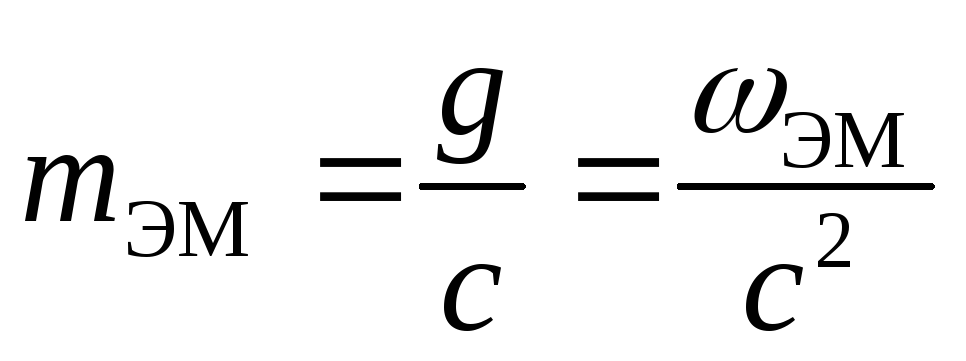
Отсюда следует:

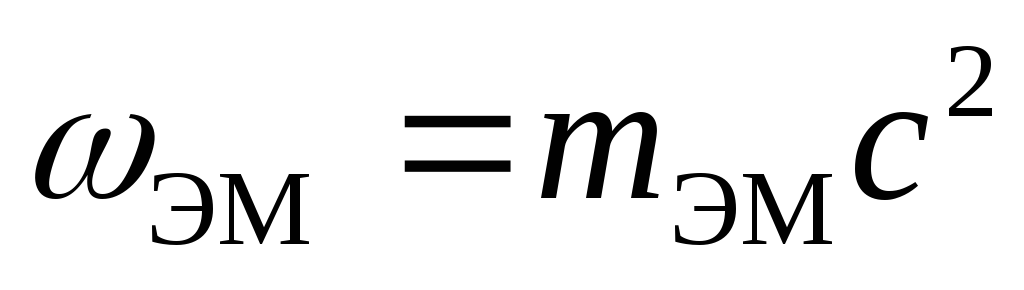
Это соотношение между массой и энергией электромагнитного поля в единичном объеме является универсальным законом природы. Согласно специальной теории относительности, оно справедливо для любых тел независимо от их природы и внутреннего строения.

Таким образом, электромагнитное поле обладает всеми признаками материальных тел – энергией, конечной скоростью распространения, импульсом, массой. Это говорит о том, что электромагнитное поле является одной из форм существования материи.

Первое экспериментальное подтверждение электромагнитной теории Максвелла было дано примерно через 15 лет после создания теории в опытах Г. Герца (1888 г.). Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства – поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Ему удалось измерить на опыте длину волны и скорость распространения электромагнитных волн, которая оказалась равной скорости света.

Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи (А. С. Попов, 1895 г.).

Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент  которого быстро изменяется во времени: p=р₀cosωt.

Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны λ (рис. 18.4).

Рис. 18.5 дает представление о структуре электромагнитной волны, излучаемой таким диполем. Следует обратить внимание на то, что максимальный поток электромагнитной энергии излучается в плоскости, перпендикулярной оси диполя. Вдоль своей оси диполь не излучает энергии. Герц использовал элементарный диполь в качестве излучающей и приемной антенн при экспериментальном доказательстве существования электромагнитных волн.

Из теории Максвелла следует, что различные электромагнитные волны имеют общую природу.

Опытами Герца была установлена идентичность природы электро­магнитного излучения и света. Из этого следовал очень важный вывод, что видимый свет представляет электромагнитное излучение. Дальней­шие исследования подтвердили, что не только видимый свет, но и инфракрасное и ультрафиолетовое излучения, рентгеновское и гамма- излучение имеют электромагнитную природу, т. е. электромагнитные волны имеют очень широкий диапазон частот или длин волн.

Спектр электромагнитного излучения охватывает радиоволны, ин­фракрасное излучение, видимый свет, ультрафиолетовое, рентгеновское и гамма-излучение. Названия для лучей, лежащих в различных областях спектра, сложились исторически. Электромагнитные волны всех участков распространяются в пространстве с одной и той же скоростью. Отлича­ются они друг от друга только длиной волны:

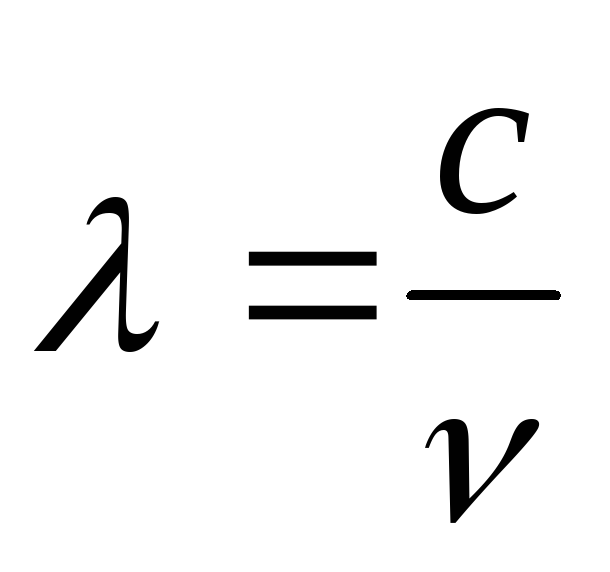
[с — скорость света, ν— частота].

Радиоволны и УКВ имеют длину волны от нескольких километров до нескольких сантиметров. Генерируют их с помощью вибраторов различных конструкций. В лабораторных условиях получено с помощью радиотехниче­ских устройств электромагнитное излучение, длина которого измеряется миллиметрами, т. е. находится в диапазоне инфракрасного излучения.

Инфракрасное излучение, видимый свет и ультрафиолетовые лучи испускают тела, нагретые до различных температур. Чем выше темпера­тура тела, тем короче длина волны испускаемых им электромагнитных волн. Рентгеновское излучение возникает при резком торможении заря­женных частиц — электронов. Гамма-излучение испускается при радио­активном распаде атомов.

Электромагнитное взаимодействие — Википедия

Электромагни́тное взаимоде́йствие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающими электрическим зарядом^[1]. С современной точки зрения электромагнитное взаимодействие между заряженными частицами осуществляется не прямо, а только посредством электромагнитного поля.

С точки зрения квантовой теории поля^[2] электромагнитное взаимодействие переносится безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля). Сам фотон электрическим зарядом не обладает, но может взаимодействовать с другими фотонами путём обмена виртуальными электрон-позитронными парами.

Из фундаментальных частиц в электромагнитном взаимодействии участвуют также имеющие электрический заряд частицы: кварки, электрон, мюон и тау-лептон (из фермионов), а также заряженные калибровочные W^±-бозоны. Остальные фундаментальные частицы Стандартной Модели (все типы нейтрино, бозон Хиггса и переносчики взаимодействий: калибровочный Z⁰-бозон, фотон, глюоны) электрически нейтральны.

Электромагнитное взаимодействие отличается от слабого^[3] и сильного^[4] взаимодействия своим дальнодействующим характером — сила взаимодействия между двумя зарядами спадает только как вторая степень расстояния (см.: закон Кулона). По такому же закону спадает с расстоянием гравитационное взаимодействие. Электромагнитное взаимодействие заряженных частиц намного сильнее гравитационного, и единственная причина, по которой электромагнитное взаимодействие не проявляется с большой силой в космических масштабах — электрическая нейтральность материи, то есть наличие в каждой области Вселенной с высокой степенью точности равных количеств положительных и отрицательных зарядов. В то же время, некоторые космологические модели, такие как плазменная космология Альфвена, предполагают, что на больших масштабах электромагнитное взаимодействие является определяющим в космических процессах.

В классических (неквантовых) рамках электромагнитное взаимодействие описывается классической электродинамикой.

В электромагнитном взаимодействии могут принимать участие только объекты, обладающие электрическим зарядом (в том числе и нейтральные в целом, но состоящие из заряженных частиц). Таковыми являются большинство известных фундаментальных элементарных частиц, в частности, все кварки, все заряженные лептоны (электрон, мюон и тау-лептон), а также заряженные калибровочные бозоны W^±. По современным представлениям электромагнитное взаимодействие осуществляется через электромагнитное поле, кванты которого — фотоны — являются переносчиками электромагнитного взаимодействия^[5].

В отличие от слабого и сильного взаимодействий, электромагнитное взаимодействие так же, как и гравитационное, является дальнодействующим. В частности, сила притяжения неподвижных противоположно заряженных тел спадает на больших расстояниях степенным образом — по закону обратного квадрата (см. закон Кулона). Дальнодействие электромагнитных сил обусловлено отсутствием массы у фотонов как переносчиков этого взаимодействия^[5].

В микромире интенсивность (эффективное сечение) электромагнитного взаимодействия характеризуется величиной постоянной тонкой структуры (в СГСЭ):

α=e2ℏc≈1137{\displaystyle \alpha ={\frac {e^{2}}{\hbar c}}\approx {\frac {1}{137}}},

где e{\displaystyle e} — элементарный электрический заряд, ℏ{\displaystyle \hbar } — постоянная Планка, c{\displaystyle c} — скорость света в вакууме. На уровне ядерных реакций по «силе» электромагнетизм занимает промежуточное положение между сильным и слабым взаимодействиями. Характерные времена распадов, вызванных электромагнитным взаимодействием, — около 10⁻¹² — 10⁻²⁰ с, в то время, как для сильного взаимодействия — порядка 10⁻²³ с, а для слабого — 10³ — 10⁻¹³ с. В качестве примера можно привести сравнение сечения рассеяния на протоне фотона с энергией 1 ГэВ и пиона с соответствующей полной энергией в системе центра масс. Для пиона, взаимодействие которого с протоном обусловлено сильным взаимодействием, сечение в 10 000 раз больше^[5].

Электромагнитное взаимодействие сохраняет пространственную чётность (так называемую Р-чётность), зарядовую чётность (так называемую C-чётность), а также такие квантовые числа, как странность, очарование, красота. Это отличает электромагнетизм от слабого взаимодействия. Одновременно, в отличие от сильного взаимодействия, электромагнитное взаимодействие в процессах с адронами не сохраняет изотопический спин (сопровождаясь испусканием фотона, он может меняться на ±1 или 0) и нарушает G-чётность^[5].

Наличие законов сохранения с учётом свойств фотонов накладывает определённые правила отбора на процессы с участием электромагнитного взаимодействия. Например, поскольку спин фотона равен 1, запрещены излучательные переходы между состояниями с нулевым моментом импульса. Необходимость сохранять зарядовую чётность приводит к тому, что системы с положительной зарядовой чётностью распадаются с испусканием только чётного количества фотонов, а с отрицательной зарядовой чётностью — только нечётного. В частности, парапозитроний распадается на два фотона, а ортопозитроний — на три (см. позитроний)^[5].

За счёт дальнодействия электромагнитное взаимодействие заметно проявляется как на макроскопическом, так и на микроскопическом уровнях. Фактически, подавляющее большинство физических сил в классической механике — силы упругости, силы трения, силы поверхностного натяжения и т. д. — имеют электромагнитную природу^[5].

Электромагнитное взаимодействие определяет большинство физических свойств макроскопических тел и, в частности, изменение этих свойств при переходе из одного агрегатного состояния в другое. Электромагнитное взаимодействие лежит в основе химических превращений. Электрические, магнитные и оптические явления также сводятся к электромагнитному взаимодействию^[5].

На микроскопическом уровне электромагнитное взаимодействие (с учётом квантовых эффектов) определяет структуру электронных оболочек атомов, структуру молекул, а также более крупных молекулярных комплексов и кластеров. В частности, величина элементарного электрического заряда определяет размеры атомов и длину связей в молекулах. Например, радиус Бора равен 4πε0ℏ2mee2{\displaystyle {{4\pi \varepsilon _{0}\hbar ^{2}} \over {m_{e}e^{2}}}}, где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная, ℏ{\displaystyle \hbar } — постоянная Планка, me{\displaystyle m_{e}} — масса электрона, e{\displaystyle e} — элементарный электрический заряд^[5].

Классическая электродинамика[править | править код]

В большинстве случаев макроскопические электромагнитные процессы с необходимой степенью точности могут быть описаны в рамках классической электродинамики. В этом случае взаимодействующие объекты рассматриваются как совокупность материальных точек, характеризуемых помимо массы также и электрическим зарядом. При этом полагается, что взаимодействие осуществляется посредством электромагнитного поля — отдельным видом материи, пронизывающим всё пространство.

Электростатика[править | править код]

Электростатика рассматривает взаимодействие неподвижных заряженных тел. Основным законом электростатики является закон Кулона, устанавливающий связь между силой притяжения/отталкивания двух заряженных материальных точек, величиной их заряда и расстоянием между ними. В математической форме закон Кулона имеет вид^[6]:

F→12=kq1q2r123r→12,{\displaystyle {\vec {F}}_{12}=k{\frac {q_{1}q_{2}}{r_{12}^{3}}}{\vec {r}}_{12},}

где F→12{\displaystyle {\vec {F}}_{12}} — сила, с которой частица 1 действует на частицу 2, q1,2{\displaystyle q_{1,2}} — величины зарядов частиц 1 и 2 соответственно, r→12{\displaystyle {\vec {r}}_{12}} — радиус-вектор, проведённый из точки расположения частицы 1 в точку расположения частицы 2 (r12{\displaystyle r_{12}} — модуль этого вектора), k{\displaystyle k} — размерный коэффициент, значение которого зависит от используемой системы единиц, в СГС он равен 1, в СИ:

k=14πε0,{\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}},}

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная.

В рамках электростатики величина электрического поля, создаваемого точечным зарядом, определяется выражением^[6]:

E→=kqr3r→,{\displaystyle {\vec {E}}=k{\frac {q}{r^{3}}}{\vec {r}},}

где E→{\displaystyle {\vec {E}}} — напряжённость электрического поля в данной точке, q{\displaystyle q} — величина заряда частицы, создающей это поле, r→{\displaystyle {\vec {r}}} — радиус-вектор, проведённый из точки расположения частицы в точку, где определяется поле (r{\displaystyle r} — модуль этого вектора).

Сила, действующая на заряженную частицу, помещённую в электрическое поле, определяется выражением:

F→=qE→,{\displaystyle {\vec {F}}=q{\vec {E}},}

где q{\displaystyle q} — величина электрического заряда частицы, E→{\displaystyle {\vec {E}}} — векторная сумма напряжённостей электрических полей, созданных всеми частицами (за исключением рассматриваемой) в точке, где находится частица^[6].

В случае, если заряд распределён в некотором объёме с плотностью ρ(r→){\displaystyle \rho ({\vec {r}})}, то электростатическое поле, создаваемое им, может быть найдено из электростатической теоремы Гаусса, имеющей в дифференциальной форме в системе СГС следующий вид^[7]:

divE→=4πρ.{\displaystyle \mathrm {div} {\vec {E}}=4\pi \rho .}

В присутствии поляризуемой диэлектрической среды величина электрического поля, создаваемого свободными зарядами, изменяется из-за влияния связанных зарядов, входящих в состав среды. Это изменение во многих случаях может быть охарактеризовано посредством введения вектора поляризации среды P→{\displaystyle {\vec {P}}} и вектора электрической индукции D→.{\displaystyle {\vec {D}}.} При этом выполняется следующее соотношение^[8]:

D→=E→+4πP→.{\displaystyle {\vec {D}}={\vec {E}}+4\pi {\vec {P}}.}

Теорема Гаусса в этом случае записывается в виде^[8]:

divD→=4πρ,{\displaystyle \mathrm {div} {\vec {D}}=4\pi \rho ,}

где под ρ{\displaystyle \rho } понимается плотность только свободных зарядов.

В большинстве случаев рассматриваемые поля значительно слабее внутриатомных полей, поэтому справедлива линейная связь между вектором поляризации и напряжённостью электрического поля в данной точке. Для изотропных сред математически этот факт выражается следующим равенством^[9]:

P→=αE→,{\displaystyle {\vec {P}}=\alpha {\vec {E}},}

где α{\displaystyle \alpha } — коэффициент, характеризующий поляризуемость данного диэлектрика при данных температуре и давлении. Аналогично, справедлива линейная связь между напряжённостью и индукцией^[9]:

D→=εE→,{\displaystyle {\vec {D}}=\varepsilon {\vec {E}},}

где коэффициент ε=1+4πα{\displaystyle \varepsilon =1+4\pi \alpha } носит название диэлектрической проницаемости^[9].

С учётом поляризуемой среды приведённые выше формулы для силы электростатического взаимодействия и напряжённости электростатического поля принимают вид^[10]:

F→12=kq1q2εr123r→12,{\displaystyle {\vec {F}}_{12}=k{\frac {q_{1}q_{2}}{\varepsilon r_{12}^{3}}}{\vec {r}}_{12},}

E→=kqεr3r→.{\displaystyle {\vec {E}}=k{\frac {q}{\varepsilon r^{3}}}{\vec {r}}.}

Магнитостатика[править | править код]

Магнитостатика изучает взаимодействие постоянных по величине и неподвижных в пространстве электрических токов, представляющих по своей сути поток заряженных частиц. В основе магнитостатики лежат закон Био — Савара — Лапласа и закон Ампера. Закон Био — Савара — Лапласа позволяет находить величину магнитного поля, создаваемого малым элементом тока. Если имеется линейный элемент тока длиною dl,{\displaystyle \mathrm {d} l,} сила тока в котором равна I,{\displaystyle {\mathcal {I}},} то он создаёт в окружающем пространстве магнитное поле, индукция которого определяется выражением^[11]:

dB→=k′I[dl→×r→]r3,{\displaystyle {\vec {\mathrm {d} B}}=k^{\prime }{\mathcal {I}}{\frac {\left[{\vec {\mathrm {d} l}}\times {\vec {r}}\right]}{r^{3}}},}

где r→{\displaystyle {\vec {r}}} — радиус-вектор, проведённый от точки расположения элемента тока до точки пространства, в которой определяется магнитное поле (r{\displaystyle r} — модуль этого радиус-вектора), dl→{\displaystyle {\vec {\mathrm {d} l}}} — вектор, длина которого равна dl,{\displaystyle \mathrm {d} l,} а направление совпадает с направлением тока I{\displaystyle {\mathcal {I}}} (считая, что направление тока определяется движением положительно заряженных частиц), k′{\displaystyle k^{\prime }} — константа, зависящая от выбора системы единиц: в системе СИ k′=μ0/4π{\displaystyle k^{\prime }=\mu _{0}/4\pi } (μ0{\displaystyle \mu _{0}} — магнитная постоянная), в системе СГС k′=1/c{\displaystyle k^{\prime }=1/c} (c{\displaystyle c} — скорость света в вакууме). Знаком × в квадратных скобках здесь и ниже обозначается векторное произведение.

Закон Ампера определяет величину силы, с которой магнитное поле в данной точке действует на элемент тока^[12]:

dF→=k′′I[dl→×B→],{\displaystyle {\vec {\mathrm {d} F}}=k^{\prime \prime }{\mathcal {I}}\left[{\vec {\mathrm {d} l}}\times {\vec {B}}\right],}

где B→{\displaystyle {\vec {B}}} — величина магнитного поля в данной точке, равная векторной сумме магнитных полей, создаваемых всеми другими токами, k′′{\displaystyle k^{\prime \prime }} — коэффициент, зависящий от выбранной системы единиц: в системе СИ он равен единице, в системе СГС — k′′=1/c{\displaystyle k^{\prime \prime }=1/c} (c{\displaystyle c} — скорость света в вакууме).

Закон Ампера является прямым следствием выражения для магнитной составляющей силы Лоренца — силы, с которой электромагнитное поле действует на заряженную частицу^[13]:

F→=k′′q[v→×B→],{\displaystyle {\vec {F}}=k^{\prime \prime }q\left[{\vec {v}}\times {\vec {B}}\right],}

где q{\displaystyle q} — заряд частицы, v→{\displaystyle {\vec {v}}} — её скорость.

Закон Био — Савара — Лапласа может быть переписан в виде для плотности тока j→{\displaystyle {\vec {j}}}^[14]:

dB→=k′[j→×r→]r3dV,{\displaystyle {\vec {\mathrm {d} B}}=k^{\prime }{\frac {\left[{\vec {j}}\times {\vec {r}}\right]}{r^{3}}}\mathrm {d} V,}

где dV{\displaystyle \mathrm {d} V} — объём элемента объёмного тока, создающего поле. Из этой формы закона Био — Савара — Лапласа можно вывести теорему о циркуляции магнитной индукции, которая в дифференциальной форме принимает вид^[15]:

rotB→=4πk′j→.{\displaystyle \mathrm {rot} {\vec {B}}=4\pi k^{\prime }{\vec {j}}.}

В присутствии магнитной среды (то есть среды, способной к намагничиванию) её влияние характеризуется векторами намагниченности среды I→{\displaystyle {\vec {I}}} и напряжённости магнитного поля H→.{\displaystyle {\vec {H}}.} При этом справедлива связь:

H→=B→μ0

Энергия электромагнитного поля — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 3 правки.

Эне́ргия электромагни́тного по́ля — энергия, заключенная в электромагнитном поле^{[источник не указан 2667 дней]}. Сюда же относятся частные случаи чистого электрического и чистого магнитного поля.

Работа электрического поля по перемещению заряда[править | править код]

Понятие работы A{\displaystyle A} электрического поля E{\displaystyle E} по перемещению заряда Q{\displaystyle Q} вводится в полном соответствии с определением механической работы:

A=∫F(x)dx=∫Q⋅E(x)dx=Q⋅U,{\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}

где U=∫Edx{\displaystyle U=\int E\,dx} — разность потенциалов (также употребляется термин напряжение).

Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t){\displaystyle U(t)}, в таком случае формулу для работы следует переписать следующим образом:

A=∫U(t)dQ=∫U(t)I(t)dt,{\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}

где I(t)=dQdt{\displaystyle I(t)={dQ \over dt}} — сила тока.

Мощность P{\displaystyle P} электрического тока для участка цепи определяется обычным образом, как производная от работы A{\displaystyle A} по времени, то есть выражением:

P(t)=dAdt=U(t)⋅I(t),{\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}

Это наиболее общее выражение для мощности в электрической цепи.

С учётом закона Ома

U=I⋅R{\displaystyle U=I\cdot R}

электрическую мощность, выделяемую на сопротивлении R{\displaystyle R}, можно выразить как через ток

P=I(t)2⋅R,{\displaystyle P=I(t)^{2}\cdot R,}

так и через напряжение:

P=U(t)2R.{\displaystyle P={{U(t)^{2}} \over R}.}

Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:

A=∫P(t)dt=∫I(t)2⋅Rdt=∫U(t)2Rdt.{\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}

Энергия электрического и магнитного полей[править | править код]

Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.

Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.

В системе СИ:

u=E⋅D2+B⋅h3.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}

В вакууме (а также в веществе при рассмотрении микрополей):

u=ε0E22+B22μ0=ε0E2+c2B22=E2/c2+B22μ0,{\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}

где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света, ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная и μ0{\displaystyle \mu _{0}} — магнитная постоянная. Иногда для констант ε0{\displaystyle \varepsilon _{0}} и μ0{\displaystyle \mu _{0}} — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.

В системе СГС:^[1]

u=E⋅D+B⋅H8π.{\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}

Энергия электромагнитного поля в колебательном контуре[править | править код]

Энергия электромагнитного поля в колебательном контуре:

W=CU22+LI22,{\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}},}

где:

U — электрическое напряжение в цепи,

C — электроемкость конденсатора,

I — сила тока,

L — индуктивность катушки или витка с током.

Потоки энергии электромагнитного поля[править | править код]

Для электромагнитной волны плотность потока энергии определяется вектором Пойнтинга S (в русской научной традиции — вектор Умова — Пойнтинга).

В системе СИ вектор Пойнтинга равен S=E×H{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} } (векторному произведению напряжённостей электрического и магнитного полей) и направлен перпендикулярно векторам E и H. Это естественным образом согласуется со свойством поперечности электромагнитных волн.

Вместе с тем, формула для плотности потока энергии может быть обобщена для случая стационарных электрических и магнитных полей и имеет тот же вид: S=E×H{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} }.

Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.

Обсуждение:Магнитное поле — Википедия

Теорема Стокса Ссылка на теорему о циркуляции к закону Ампера отношения не имеет

а выводов чаво нету?

А какие должны быть-то, мило́й? Здесь не доклад и не урок 🙂 infovarius 14:46, 8 января 2010 (UTC)

Магнитное поле — силовое свойство электрического поля[править код]

Mагнитное поле в Wikipedia (WP) рассматривается как один из видов материи (магнитная материя) и одновременно как релятивистская составляющая электрического поля (также по определению WP один из видов материи − электрическая материя). Отсюда приходим к выводу: магнитное поле − магнитная материя, являющаяся релятивистской составляющей электрической материи. Неопределенность и загадочность такой формулировки, полностью лишенной наглядности, здесь вполне очевидны.

Предлагаемое альтернативное определение рассматривает магнитное поле как одно из проявлений силовых свойств электрического поля. Тем самым две сущности (магнитное и электрическое поля) сводятся к одной − электрическому полю. Однозначность альтернативного определения гарантируется его выражением в виде формул, указывающим на конкретное свойство электрического поля в точке наблюдения − его завихрённость (наличие ротации). Это свойство электрического поля возникает при движении электрических зарядов вследствие конечной скорости с ( с − скорость света) распространения их электрических (кулоновских) полей (эффект запаздывания). При таком подходе переменное и стационарное магнитные поля, например, для магнитной индукции B бесконечно-длинного прямолинейного провода с током могут быть представлены в следующем виде:

1. Переменное магнитное поле [СИ]. Из уравнений Максвелла для отдельной гармоники B непосредственно имеем:

                                                                               B=(i/w)rotE ,

где E и B – комплексные амплитуды электрического и магнитного полей в точке наблюдения; i − мнимая единица, w – круговая частота.

2. Стационарное магнитное поле [СИ]. Для магнитной индукции B согласно работе (Б.Г. Сапожников «Запаздывающее электрическое поле постоянного тока», 2010) http://www.hge.pu.ru/index.php?option=com_content&task=view&id=2263&Itemid=120 имеем:

                                                                             B=(-4r/πc)rotE',

где E’ – запаздывающее электрическое поле постоянного тока, r – расстояние от оси провода до точки наблюдения.

Альтернативное определение магнитного поля гарантирует также наглядность определения − возможность непосредственного объяснения рассматриваемого свойства. Так, например, траектория электрона, пролетающего через стационарное однородное электрическое поле с указанным свойством (с постоянным магнитным полем) в общем случае закручивается в спираль. Причем, чем интенсивнее магнитное поле (больше завихрённость запаздывающего электрического поля E’ ), тем выше плотность “намотки” витков спирали.

Более подробно об альтернативном определении магнитного поля см. приведенную ссылку, которую можно найти также через Google. (195.70.202.10 17:48, 31 января 2011 (UTC))

Известно [2], что существование стационарного магнитного поля зависит от субъективного выбора системы координат. В подвижной системе движущемуся электрическому заряду отвечает магнитное поле (особый вид материи по определению WP). В случае выбора неподвижной системы с неподвижным зарядом — материя исчезает, нарушая, к сожалению, определение этой философской категории и подвергая сомнению определение магнитного поля WP. В то же время свойство объекта может быть разным в различных системах. По этой причине при субъективном изменении системы координат предлагаемому определению магнитного поля не грозит фатальный исход.

Уважаемые коллеги! Просьба серьезно отнестись к альтернативному определению магнитного поля и принять участие в его обсуждении и критике с целью устранения возможных физ.-мат. ошибок и при желании — с целью участия в дальнейшей разработке вопроса. Доп.ссылка http://www.hge.pu.ru/index.php?option=com_content&task=view&id=2532&Itemid=120 Для обсуждения предлагается почтовый адрес [email protected] с тем, чтобы не нарушать сложившиеся правила WP (статьи и обсуждение (?) на территории WP возможны только на основе обобщения и противопоставления друг другу авторитетных источников, избегая оригинальных опубликованных (депонированных) исследований и собственного мнения, отличающегося от авторитетного). (195.70.202.10 08:45, 3 февраля 2011 (UTC))

Цитата из Г. В. Николаева[править код]

Магнитное поле — проявление электрического в результате движения зарядов из-за конечной скорости распространения взаимодействия, можно считать математически удобным понятием, но не самостоятельным полем. Если магнитное поле считать самостоятельным физическим полем пусть даже в составе элетромагнитного, то это приводит к парадоксам когда магнитное поле то существует то не существует в зависимости от выбора системы отсчета. Николаев Г.В. «Современная электродинамика»: стр. 29 — «…в свое время Ампер, Гроссман, Гаусс, Ленц, Нейман, Вебер, Риман и др. стояли на точке зрения, что, не обращаясь к понятию «магнитного поля», любые магнитные взаимодействия можно свести к обычным взаимодействиям токовых элементов или движущихся зарядов…» вывод можно посмотреть в той же книжке. Ruslan Gubaidullin 10:32, 28 марта 2011 (UTC)

• Г. В. Николаев — очень плохой физик. Не читайте его. — Артём Коржиманов 10:44, 28 марта 2011 (UTC)

Нейтральность и объективность. Плохой-хороший время покажет.

Если точка зрения на какой-то объект имеет место в обществе в энциклопедии можно об этом указать. Это ведь не единственный человек который вносит поправку в понятие магнитное поле Ву Хыу Тоян. Ruslan Gubaidullin 10:51, 28 марта 2011 (UTC)

• См. ВП:МАРГ: «Из статей на научную тематику следует исключать предположения, не подвергавшиеся критическому анализу научным сообществом или отвергнутые им.» — Артём Коржиманов 11:41, 28 марта 2011 (UTC)

Семиков С.А. АЛЬТЕРНАТИВНАЯ ЭЛЕКТРОДИНАМИКА АЛЬТЕРНАТИВНАЯ ЭЛЕКТРОДИНАМИКА (К 100-летней годовщине смерти Вальтера Ритца) напечатано в журнале Инженер №8-9, 2009

ВАЛЬТЕР РИТЦ КРИТИЧЕСКИЙ АНАЛИЗ ОБЩЕЙ ЭЛЕКТРОДИНАМИКИ

Гришаев А.А. РАЗНОИМЁННЫЕ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ, КАК ПРОТИВОФАЗНЫЕ КВАНТОВЫЕ ПУЛЬСАЦИИ

Петров Ю.И. Некоторые фундаментальные представления физики: критика и анализ. Серия «Relata Refero» ISBN 5-484-00290-7 Во второй главе выясняется смысл магнитного поля и законов электродинамики. В соответствии с представлениями Ампера установлено, что магнитное поле является фиктивной, хотя и очень полезной в расчетах, величиной

И т.д. —Ruslan Gubaidullin 13:01, 28 марта 2011 (UTC)

• Все эти источники не относятся к академическим. — Артём Коржиманов 14:38, 28 марта 2011 (UTC)

МАРГ «Например, отсутствие критики креационизма в рецензируемых журналах не должно быть основанием для того, чтобы отодвигать научную критику этой теории на задний план или вовсе удалять её из статьи — рецензируемые журналы попросту не печатают статей на эту тему, а представление о взглядах сторонников этой теории также можно получить лишь из материалов, не прошедших экспертной оценки» — отсутствие как критики так и АИ не является препятствием. НТЗ-основное правило

На месте картинки с опилками, моё мнение, лучше бы поместить картинку с линиями равной магнитной напряжённости. Картинка была бы намного информативнее. А потом как пример притяжения ферромагнитных опилок градиентом поля поместить ту картинку которая есть.

И ещё: показать рядом вокруг сечения проводов соленоида кружочки с равной папряжённостью магнитного поля. А только далее пойдут линии. Как пример невозможности бытия плоских электромагнитных волн — то же что и небытие монополя Дирака.

С уважением. (андроид) 91.205.25.30 23:48, 20 февраля 2013 (UTC)

СТО специальная теория относительности[править код]

Эйн.. правильно Айнштайн — не являетсся автором этой теории, а им является Лоренц. А.А. лишь интерпретатор теории Лоренца, а вся математика и все формулы уже в СТО Лоренца. Математически эквивалетнтые теории. А.А отверг лишь «необнаруживаемый этэр», который предполагал Лоренц и Пуанкаре после результата Михельсона и Морли. Результат этот явно был ненаучно сверхинтерпретирован как «несуществование этэра» тогда как его значение лишь факт, что не найден именно искомый этэр с этэрным ветром. А неизвестные этэры без этэрного ветра естественно не могли быть исключены, что сделали Лорэнц и Пуанкре как ученный.

И конечная скорость света и конртрактация длин и дилатация времени уже в СТО Лорэнца. Все это приписывают А.А. А.А. утверждал, что не читал работ Лорэнца, хотя те были в том же журнале и тема вся именно Лорэнца до АА.

Но в 1920м г А.А. в своей речи в Ляйдэне пел песнь во славу этэра, по его словам «без этэра нет ничего». и «искривления пространства есть этэр общей теории относительности».

Все популярные примеры СТО от близнецов и прочих ракет, пролетающих сквоь сквозной гараж написаны другими авторами, не Айнштаном, но приписаны тоже ему. Все эти примеры точно также дейтсвительны для СТО Лорэнца.

В данной статье написано, что магнитное поле есть особая материя. Что соврешенно подходит под «необнаруживаемый этэр» Лорэнца. Вся квантовая механика говорит об именно чем-то в непустом пространстве. что опять же подходит под необнаруживаемый этэр Лорэнца. А.А. видимо верил в свою безэтэрность до ОТО. Но обьяснить что и как передает силы магнитного или электрического поля он не мог, исключив этэр.

5.28.91.44 13:33, 18 августа 2018 (UTC)

Электромагнитное излучение — Википедия

Электромагни́тные во́лны / электромагни́тное излуче́ние — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.^[1]

Среди электромагнитных полей, порождённых электрическими зарядами и их движением, принято относить к излучению ту часть переменных электромагнитных полей, которая способна распространяться наиболее далеко от своих источников — движущихся зарядов, затухая наиболее медленно с расстоянием.

Электромагнитные волны подразделяются на:

Электромагнитное излучение способно распространяться практически во всех средах. В вакууме (пространстве, свободном от вещества и тел, поглощающих или испускающих электромагнитные волны) электромагнитное излучение распространяется без затуханий на сколь угодно большие расстояния, но в ряде случаев достаточно хорошо распространяется и в пространстве, заполненном веществом (несколько изменяя при этом своё поведение).

Классификация диапазонов спектра электромагнитного излучения по-английски. Колонки: 1 (чёрная) — аббревиатуры обозначения диапазонов, 2 — частота, 3 — длина волны, 4 — энергия фотона

Характеристики электромагнитного излучения[править | править код]

Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию.

Длина волны прямо связана с частотой через (групповую) скорость распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше. Фазовая скорость электромагнитного излучения в вакууме также равна скорости света, в различных средах она может быть как меньше, так и больше скорости света^[2].

Описанием свойств и параметров электромагнитного излучения в целом занимается электродинамика, хотя свойствами излучения отдельных областей спектра занимаются определённые более специализированные разделы физики (отчасти так сложилось исторически, отчасти обусловлено существенной конкретной спецификой, особенно в отношении взаимодействия излучения разных диапазонов с веществом, отчасти также спецификой прикладных задач). К таким более специализированным разделам относятся оптика (и её разделы) и радиофизика. Жёстким электромагнитным излучением коротковолнового конца спектра занимается физика высоких энергий^[3]; в соответствии с современными представлениями (см. Стандартная модель), при высоких энергиях электродинамика перестаёт быть самостоятельной, объединяясь в одной теории со слабыми взаимодействиями, а затем — при ещё более высоких энергиях — как ожидается — со всеми остальными калибровочными полями.

Существуют различающиеся в деталях и степени общности теории, позволяющие смоделировать и исследовать свойства и проявления электромагнитного излучения. Наиболее фундаментальной^[4] из завершённых и проверенных теорий такого рода является квантовая электродинамика, из которой путём тех или иных упрощений можно в принципе получить все перечисленные ниже теории, имеющие широкое применение в своих областях. Для описания относительно низкочастотного электромагнитного излучения в макроскопической области используют, как правило, классическую электродинамику, основанную на уравнениях Максвелла, причём существуют упрощения в прикладных применениях. Для оптического излучения (вплоть до рентгеновского диапазона) применяют оптику (в частности, волновую оптику, когда размеры некоторых частей оптической системы близки к длинам волн; квантовую оптику, когда существенны процессы поглощения, излучения и рассеяния фотонов; геометрическую оптику — предельный случай волновой оптики, когда длиной волны излучения можно пренебречь). Гамма-излучение чаще всего является предметом ядерной физики, с других — медицинских и биологических — позиций изучается воздействие электромагнитного излучения в радиологии. Существует также ряд областей — фундаментальных и прикладных — таких, как астрофизика, фотохимия, биология фотосинтеза и зрительного восприятия, ряд областей спектрального анализа, для которых электромагнитное излучение (чаще всего — определенного диапазона) и его взаимодействие с веществом играют ключевую роль. Все эти области граничат и даже пересекаются с описанными выше разделами физики.

Некоторые особенности электромагнитных волн c точки зрения теории колебаний и понятий электродинамики:

• электромагнитные волны в свободном пространстве — это поперечные волны, в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, но они существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приёмнику в том числе и через вакуум.

Диапазоны электромагнитного излучения[править | править код]

Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения (в вакууме) постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.

Ультракороткие радиоволны принято разделять на метровые, дециметровые, сантиметровые, миллиметровые и децимиллиметровые волны (гипервысокие частоты, ГВЧ, 300—3000 ГГц) — стандартные диапазоны радиоволн по общепринятой классификации^[5]. По другой классификации указанные стандартные диапазоны радиоволн, исключая метровые волны, называют микроволнами или волнами сверхвысоких частот (СВЧ)^[6].

Ионизирующее электромагнитное излучение. К этой группе традиционно относят рентгеновское и гамма-излучение, хотя, строго говоря, ионизировать атомы может и ультрафиолетовое излучение, и даже видимый свет. Границы областей рентгеновского и гамма-излучения могут быть определены лишь весьма условно. Для общей ориентировки можно принять, что энергия рентгеновских квантов лежит в пределах 20 эВ — 0,1 МэВ, а энергия гамма-квантов — больше 0,1 МэВ. В узком смысле гамма-излучение испускается ядром, а рентгеновское — атомной электронной оболочкой при выбивании электрона с низколежащих орбит, хотя эта классификация неприменима к жёсткому излучению, генерируемому без участия атомов и ядер (например, синхротронному или тормозному излучению).

Радиоволны[править | править код]

Из-за больших значений λ распространение радиоволн можно рассматривать без учёта атомистического строения среды. Исключение составляют только самые короткие радиоволны, примыкающие к инфракрасному участку спектра. В радиодиапазоне слабо сказываются и квантовые свойства излучения, хотя их всё же приходится учитывать, в частности, при описании квантовых генераторов и усилителей сантиметрового и миллиметрового диапазонов, а также молекулярных стандартов частоты и времени, при охлаждении аппаратуры до температур в несколько кельвинов.

Радиоволны возникают при протекании по проводникам переменного тока соответствующей частоты. И наоборот, проходящая в пространстве электромагнитная волна возбуждает в проводнике соответствующий ей переменный ток. Это свойство используется в радиотехнике при конструировании антенн.

Естественным источником волн этого диапазона являются грозы. Считается, что они же являются источником стоячих электромагнитных волн Шумана.

Микроволновое излучение[править | править код]

Инфракрасное излучение (тепловое)[править | править код]

Видимое излучение (оптическое)[править | править код]

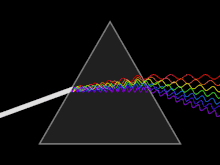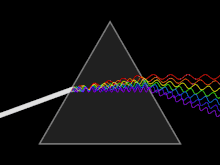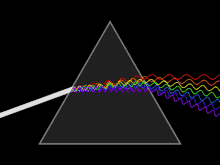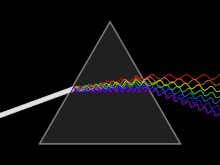Прозрачная призма разлагает луч белого цвета на составляющие его лучи^[7]

Видимое, инфракрасное и ультрафиолетовое излучение составляет так называемую оптическую область спектра в широком смысле этого слова. Выделение такой области обусловлено не только близостью соответствующих участков спектра, но и сходством приборов, применяющихся для её исследования и разработанных исторически главным образом при изучении видимого света (линзы и зеркала для фокусирования излучения, призмы, дифракционные решётки, интерференционные приборы для исследования спектрального состава излучения и пр.).

Частоты волн оптической области спектра уже сравнимы с собственными частотами атомов и молекул, а их длины — с молекулярными размерами и межмолекулярными расстояниями. Благодаря этому в этой области становятся существенными явления, обусловленные атомистическим строением вещества. По этой же причине, наряду с волновыми, проявляются и квантовые свойства света.

Самым известным источником оптического излучения является Солнце. Его поверхность (фотосфера) нагрета до температуры 6000 K и светит ярко-белым светом (максимум непрерывного спектра солнечного излучения расположен в «зелёной» области 550 нм, где находится и максимум чувствительности глаза). Именно потому, что мы родились возле такой звезды, этот участок спектра электромагнитного излучения непосредственно воспринимается нашими органами чувств.

Излучение оптического диапазона возникает, в частности, при нагревании тел (инфракрасное излучение называют также тепловым) из-за теплового движения атомов и молекул. Чем сильнее нагрето тело, тем выше частота, на которой находится максимум спектра его излучения (см.: Закон смещения Вина). При определённом нагревании тело начинает светиться в видимом диапазоне (каление), сначала красным цветом, потом жёлтым и так далее. И наоборот, излучение оптического спектра оказывает на тела тепловое воздействие (см.: Болометрия).

Оптическое излучение может создаваться и регистрироваться в химических и биологических реакциях. Одна из известнейших химических реакций, являющихся приёмником оптического излучения, используется в фотографии. Источником энергии для большинства живых существ на Земле является фотосинтез — биологическая реакция, протекающая в растениях под действием оптического излучения Солнца.

Ультрафиолетовое излучение[править | править код]

Жёсткое излучение[править | править код]

В области рентгеновского и гамма-излучения на первый план выступают квантовые свойства излучения.

Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате процессов, происходящих внутри электронных оболочек атомов. Гамма-излучение появляется в результате процессов, происходящих внутри атомных ядер, а также в результате превращения элементарных частиц.

Особенности электромагнитного излучения разных диапазонов[править | править код]

Распространение электромагнитных волн, временны́е зависимости электрического E(t){\displaystyle {\mathit {E}}(t)} и магнитного H(t){\displaystyle {\mathit {H}}(t)} полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.

Электромагнитные излучения различных частот взаимодействуют с веществом также по-разному. Процессы излучения и поглощения радиоволн обычно можно описать с помощью соотношений классической электродинамики; а вот для волн оптического диапазона и, тем более, жёстких лучей необходимо учитывать уже их квантовую природу.

• Первые волновые теории света (их можно считать старейшими вариантами теорий электромагнитного излучения) восходят по меньшей мере к временам Гюйгенса, когда они получили уже и заметное количественное развитие. В 1678 году Гюйгенс выпустил «Трактат о свете» (фр. Traité de la lumière^[en]) — набросок волновой теории света. Другое замечательное сочинение он издал в 1690 году; там он изложил качественную теорию отражения, преломления и двойного лучепреломления в исландском шпате в том самом виде, как она излагается теперь в учебниках физики. Сформулировал так называемый принцип Гюйгенса, позволяющий исследовать движение волнового фронта, впоследствии развитый Френелем (принцип Гюйгенса — Френеля) и сыгравший важную роль в волновой теории света, и теории дифракции. В 1660—1670-е годы существенный теоретический и экспериментальный вклад в физическую теорию света внесли также Ньютон и Гук.
• Многие положения корпускулярно-кинетической теории М. В. Ломоносова (1740—1750-е годы) предвосхищают постулаты электромагнитной теории: вращательное («коловратное») движение частиц как прообраз электронного облака, волновая («зыблющаяся») природа света, общность её с природой электричества, отличие от теплового излучения и т. д.
• В 1800 году английский учёный У. Гершель открыл инфракрасное излучение.
• В 1801 году Риттер открыл ультрафиолетовое излучение^[8].
• Существование электромагнитных волн предсказал английский физик Фарадей в 1832 году.
• В 1865 году английский физик Дж. Максвелл завершил построение теории электромагнитного поля классической (неквантовой) физики, строго оформив её математически, и на её основе получив твёрдое обоснование существования электромагнитных волн, а также найдя скорость их распространения (неплохо совпадавшую с известным тогда значением скорости света), что позволило ему обосновать и предположение о том, что свет является электромагнитной волной.
• В 1888 году немецкий физик Герц подтвердил теорию Максвелла опытным путём. Интересно, что Герц не верил в существование этих волн и проводил свой опыт с целью опровергнуть выводы Максвелла.
• 8 ноября 1895 года Рентген открыл электромагнитное излучение (получившее впоследствии название рентгеновского) более коротковолнового диапазона, чем ультрафиолетовое.
• В конце XIX столетия белорусский ученый, профессор Я. Наркевич-Иодко впервые в мире исследовал возможности использования электромагнитного излучения газоразрядной плазмы для электрографии (визуализации) живых организмов, то есть для нужд практической медицины.
• В 1900 году Поль Виллар при изучении излучения радия открыл гамма-излучение.
• В 1900 году Планк при теоретическом исследовании проблемы излучения абсолютно чёрного тела открывает квантованность процесса электромагнитного излучения. Эта работа стала началом квантовой физики.
• Начиная с 1905 года Эйнштейн, а затем и Планк публикуют ряд работ, приведших к формированию понятия фотона, что стало началом создания квантовой теории электромагнитного излучения.
• Дальнейшие работы по квантовой теории излучения и его взаимодействия с веществом, приведшие в итоге к формированию квантовой электродинамики в её современном виде, принадлежат ряду ведущих физиков середины XX века, среди которых можно выделить, применительно именно к вопросу квантования электромагнитного излучения и его взаимодействия с веществом, кроме Планка и Эйнштейна, Бозе, Бора, Гейзенберга, де Бройля, Дирака, Фейнмана, Швингера, Томонагу.

Излучения электромагнитного диапазона при определённых уровнях могут оказывать отрицательное воздействие на организм человека, животных и других живых существ, а также неблагоприятно влиять на работу электрических приборов. Различные виды неионизирующих излучений (электромагнитных полей, ЭМП) оказывают разное физиологическое воздействие. На практике выделяют диапазоны магнитного поля (постоянного и квазипостоянного, импульсного), ВЧ- и СВЧ-излучений, лазерного излучения, электрического и магнитного поля промышленной частоты от высоковольтного оборудования и др.

Влияние на живые существа[править | править код]

Существуют национальные и международные гигиенические нормативы уровней ЭМП, в зависимости от диапазона, для селитебной зоны и на рабочих местах.

Оптический диапазон[править | править код]

Существуют гигиенические нормы освещённости; также разработаны нормативы безопасности при работе с лазерным излучением.

Радиоволны[править | править код]

Допустимые уровни электромагнитного излучения (плотность потока электромагнитной энергии) отражаются в нормативах, которые устанавливают государственные компетентные органы, в зависимости от диапазона ЭМП. Эти нормы могут быть существенно различны в разных странах.

Установлены биологические последствия сильного воздействия полей высоких уровней (значительно выше 100 µT), которые объясняются действием признанных биофизических механизмов. Внешние магнитные поля крайне низкой частоты (КНЧ) индуцируют электрические поля и токи в организме человека, которые, при очень высокой мощности поля, оказывают стимулирующее воздействие на нервы и мышцы и вызывают изменение возбудимости нервных клеток в центральной нервной системе.

Что касается долгосрочных последствий, то ввиду недостаточности фактических данных, подтверждающих связь между воздействием магнитных полей КНЧ и детской лейкемией, польза для здоровья от снижения уровней воздействия представляется неясной.^[9]

В ряде исследований было изучено воздействие радиочастотных полей на электрическую активность мозга, когнитивные функции, сон, сердечный ритм и кровяное давление у добровольцев. На сегодняшний день исследования не предполагают каких-либо последовательных доказательств неблагоприятного воздействия на здоровье от воздействия радиочастотных полей на уровнях ниже уровней, которые вызывают нагревание тканей. Кроме того, исследования не смогли обнаружить причинно-следственную связи между воздействием электромагнитных полей и «симптомами самооценки» или «электромагнитной гиперчувствительностью». Эпидемиологические исследования, изучающие потенциальные долгосрочные риски от радиочастотного воздействия, в основном имели цель найти связь между опухолями головного мозга и использованием мобильных телефонов. Результаты исследований на животных не показывают повышенного риска развития рака от долгосрочного воздействия радиочастотных полей.^[10]

Эти данные не должны быть причиной для радиофобии, однако очевидна необходимость в существенном углублении сведений о действии ЭМИ на живые организмы.

В России с 2017 года действует СанПиН 2.2.4.3359-16 «Санитарно-эпидемиологические требования к физическим факторам на рабочих местах. Санитарно-эпидемиологические правила и нормативы»^[11], заменивший и отменивший ранее действовавшие отдельные гигиенические нормативы.

• Допустимые уровни излучения различных передающих радиотехнических средств на частотах >300 МГц в санитарно-селитебной зоне в некоторых странах заметно различаются:

Россия, Украина, Польша, Беларусь, Казахстан: 10 мкВт/см².

США, Европа (за исключением некоторых стран), Япония, Корея: 200 — 1000 мкВт/см².^[12][13]

Канада: 130 — 2000 мкВт/см².^[14]

Китай: 10 (40) — 2000 мкВт/см².^[15][16]

Параллельное развитие гигиенической науки в СССР и западных странах привело к формированию разных подходов к оценке действия ЭМИ. Для части стран постсоветского пространства сохраняется преимущественно нормирование в единицах плотности потока энергии (ППЭ), а для США и стран ЕС типичным является оценка удельной мощности поглощения (SAR).

«Современные представления о биологическом действии ЭМИ от мобильных радиотелефонов (МРТ) не позволяют прогнозировать все неблагоприятные последствия, многие аспекты проблемы не освещены в современной литературе и требуют дополнительных исследований. В связи с этим, согласно рекомендациям ВОЗ, целесообразно придерживаться предупредительной политики, т. е. максимально уменьшить время использования сотовой связи».

Ионизирующее излучение[править | править код]

Допустимые нормативы регулируются нормами радиационной безопасности — НРБ-99.

Влияние на радиотехнические устройства[править | править код]

Существуют административные и контролирующие органы — инспекция по радиосвязи (на Украине, например, Украинский частотный надзор, который регулирует распределение частотных диапазонов для различных пользователей, соблюдение выделенных диапазонов, отслеживает незаконное пользование радиоэфиром).

1. ↑ Петрусевич Ю.М. Излучения // Большая медицинская энциклопедия : в 30 т. / гл. ред. Б.В. Петровский. — 3 изд. — Москва : Советская энциклопедия, 1978. — Т. 9. Ибн-Рошд — Йордан. — 483 с. — 150 300 экз.
2. ↑ (Принцип максимальности скорости света теории относительности при этом не нарушается, так как скорость переноса энергии и информации — связанная с групповой, а не фазовой скоростью — в любом случае не превышает световой скорости)
3. ↑ Также вопросы, связанные с жесткими и сверхжесткими излучениями могут возникать в астрофизике; там иногда они имеют особую специфику, например, генерация излучения может происходить в областях огромного размера.
4. ↑ Наиболее фундаментальной, не считая упомянутых выше теорий Стандартной модели, отличия которой от чистой квантовой электродинамики проявляются, впрочем, лишь при очень высоких энергиях.
5. ↑ ^{1 2} ГОСТ 24375-80. Радиосвязь. Термины и определения
6. ↑ 48.Особенности диапазона свч. Деление свч диапазона на поддиапазоны. (неопр.). StudFiles. Дата обращения 24 октября 2017.
7. ↑ Структура луча показана условно. Синусоидальность лучей показана условно. Разная скорость света в призме для разных длин волн не показана.
8. ↑ Догадки о наличии излучения за пределами видимого спектра высказывались и ранее Гершеля и Риттера, однако они показали это экспериментально.
9. ↑ [http://www.who.int/peh-emf/publications/facts/fs322_ELF_fields_russian.pdf Электромагнитные поля и общественное здравоохранение] (неопр.). Всемирная организация здравоохранения (Июнь 2007 г.).
10. ↑ Electromagnetic fields and public health: mobile phones (неопр.). Всемирная организация здравоохранения (Октябрь 2014 г.).
11. ↑ http://docs.cntd.ru/document/420362948
12. ↑ https://transition.fcc.gov/bureaus/oet/info/documents/bulletins/oet65/oet65.pdf
13. ↑ https://www.icnirp.org/cms/upload/publications/ICNIRPemfgdl.pdf
14. ↑ https://www.canada.ca/content/dam/hc-sc/migration/hc-sc/ewh-semt/alt_formats/pdf/consult/_2014/safety_code_6-code_securite_6/final-finale-eng.pdf
15. ↑ http://www.nhc.gov.cn/ewebeditor/uploadfile/2014/11/20141103161157888.pdf
16. ↑