Кластеризация (кластерный анализ): что это такое

Кластеризация — это разбиение множества объектов на подмножества (кластеры) по заданному критерию. Каждый кластер включает максимально схожие между собой объекты. Представим переезд: нужно разложить по коробкам вещи по категориям (кластерам) — например одежда, посуда, декор, канцелярия, книги. Так удобнее перевозить и раскладывать предметы в новом жилье. Процесс сбора вещей по коробкам и будет кластеризацией.

Критерии кластеризации определяет человек, а не алгоритм, — этим она отличается от классификации. Этот метод машинного обучения (Machine Learning) часто применяют в различных неструктурированных данных — например если нужно автоматически разбить коллекцию изображений на мини-группы по цветам.

Визуализация кластеризации. Источник

Кластерный анализ применяют в разных сферах:

• в маркетинге — для сегментирования клиентов, конкурентов, исследования рынка;
• медицине — для кластеризации симптомов, заболеваний, препаратов;
• биологии — для классификации животных и растений;
• социологии — для разбиения респондентов на однородные группы;
• компьютерных науках — для группировки результатов при поиске сайтов, файлов и других объектов.

Курс Уверенный старт в IT Поможем определить подходящую вам IT-профессию и освоить её с нуля. Вы на практике попробуете разные направления: разработку на разных языках, аналитику данных, Data Science, менеджмент в IT. Это самый подходящий курс для построения карьеры в IT в новой реальности.

Подробнее

Объект описывается при помощи набора характеристик. Признаки бывают числовые и категориальные. Например, можно кластеризовать группу покупателей на основе их покупок в интернет-магазине. В качестве входных данных будут средний чек, возраст, количество покупок в месяц, любимая категория покупок и другие критерии.

Это симметричная таблица, где по строкам и столбцам расположены объекты, а на пересечении — расстояние между ними: например, таблица с расстояниями между отелями в разных городах. Такой способ может помочь выделить кластеры отелей, которые сгруппированы в одной и той же локации.

Кластеризация актуальна, если исходная выборка слишком большая. В результате от каждого кластера остается по одному типичному представителю. Количество кластеров может быть любым — здесь важно обеспечить максимальное сходство объектов внутри каждой группы.

Разбиение объектов на кластеры позволяет добавить дополнительный признак каждому объекту. Так, если в результате кластерного анализа выявилось, что определенный покупатель относится к первому кластеру, и мы знаем, что первый кластер — это кластер людей, которые тратят большое количество денег на покупки по средам, то можно сказать, что это покупатель приобретает продукты в основном по средам.

В этом случае выделяют нетипичные объекты, не подходящие ни к одному сформированному кластеру. Интересны отдельные объекты, которые не вписываются ни в одну из сформированных групп.

Общепринятой классификации методов нет, но есть несколько групп подходов.

1. Вероятностный подход. В рамках него предполагается, что каждый из объектов относится к одному из классов.

• EM-алгоритм применяется для нахождения оценок максимального правдоподобия параметров вероятностных моделей (если есть зависимость от скрытых переменных).
• K-средних — алгоритм минимизирует суммарное квадратичное отклонение точек кластеров от их центров.
• Алгоритмы семейства FOREL основаны на идее объединения объектов в один кластер в областях их максимальной концентрации.

2. Подходы с учетом систем искусственного интеллекта. Большая условная группа методов, разнится с методической точки зрения.

• Метод нечеткой кластеризации C-средних предполагает разбиение имеющегося множества элементов на определенное число нечетких множеств. Метод является усовершенствованным вариантом К-средних.
• Нейронная сеть Кохонена — класс нейронных сетей со слоем Кохонена, состоящим из линейных формальных нейронов.
• Генетический алгоритм — алгоритм поиска, применяемый для решения задач оптимизации и моделирования с помощью случайного подбора, вариации и комбинирования искомых параметров. Используются механизмы, аналогичные естественному отбору в природе.

4. Иерархический подход. Предполагает наличие вложенных групп — кластеров разного порядка. Выделяются агломеративные и дивизионные (объединительные и разделяющие) алгоритмы. В зависимости от количества признаков могут выделяться политетические (используют при сравнении нескольких признаков одновременно) и монотетические (используют при применении одного признака) методы классификации.

В кластеризации имеют дело с множеством объектов (X) и множеством номеров кластеров (Y). Задана функция расстояния между объектами (p). Нужно разбить обучающую выборку на кластеры, так чтобы каждый кластер состоял из объектов, близких по метрике p, а объекты разных кластеров существенно отличались. При этом каждому объекту приписывается номер кластера y(i).

Алгоритм кластеризации — это функция, которая любому объекту X ставит в соответствие номер кластера Y.

Обзор алгоритмов кластеризации данных / Хабр

Приветствую!

В своей дипломной работе я проводил обзор и сравнительный анализ алгоритмов кластеризации данных. Подумал, что уже собранный и проработанный материал может оказаться кому-то интересен и полезен.
О том, что такое кластеризация, рассказал sashaeve в статье «Кластеризация: алгоритмы k-means и c-means». Я частично повторю слова Александра, частично дополню. Также в конце этой статьи интересующиеся могут почитать материалы по ссылкам в списке литературы.

Так же я постарался привести сухой «дипломный» стиль изложения к более публицистическому.

Понятие кластеризации

Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.

Применение кластерного анализа в общем виде сводится к следующим этапам:

1. Отбор выборки объектов для кластеризации.
2. Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных.
3. Вычисление значений меры сходства между объектами.
4. Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
5. Представление результатов анализа.

После получения и анализа результатов возможна корректировка выбранной метрики и метода кластеризации до получения оптимального результата.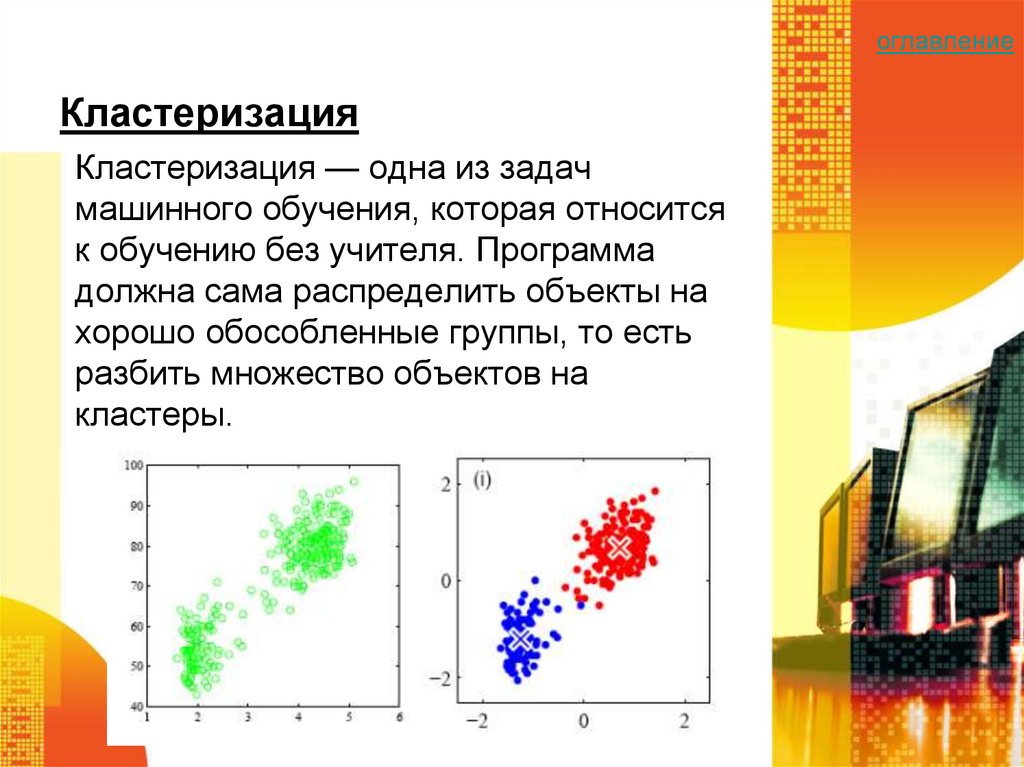

Меры расстояний

Итак, как же определять «похожесть» объектов? Для начала нужно составить вектор характеристик для каждого объекта — как правило, это набор числовых значений, например, рост-вес человека. Однако существуют также алгоритмы, работающие с качественными (т.н. категорийными) характеристиками.

После того, как мы определили вектор характеристик, можно провести нормализацию, чтобы все компоненты давали одинаковый вклад при расчете «расстояния». В процессе нормализации все значения приводятся к некоторому диапазону, например, [-1, -1] или [0, 1].

Наконец, для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик, вот лишь основные из них:

1. Евклидово расстояние
   Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:
   
   
2. Квадрат евклидова расстояния
   Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
   
   
3. Расстояние городских кварталов (манхэттенское расстояние)
   Это расстояние является средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако для этой меры влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:
   
   
   
4. Расстояние Чебышева
   Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой-либо одной координате. Расстояние Чебышева вычисляется по формуле:
   
   
5. Степенное расстояние
   Применяется в случае, когда необходимо увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле:
   ,
   где r и p – параметры, определяемые пользователем. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра – r и p — равны двум, то это расстояние совпадает с расстоянием Евклида.

Выбор метрики полностью лежит на исследователе, поскольку результаты кластеризации могут существенно отличаться при использовании разных мер.

Классификация алгоритмов

Для себя я выделил две основные классификации алгоритмов кластеризации.

1. Иерархические и плоские.
   Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.о. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.
   Плоские алгоритмы строят одно разбиение объектов на кластеры.
2. Четкие и нечеткие.
   Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.

Объединение кластеров

В случае использования иерархических алгоритмов встает вопрос, как объединять между собой кластера, как вычислять «расстояния» между ними. Существует несколько метрик:

1. Одиночная связь (расстояния ближайшего соседа)
   В этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Результирующие кластеры имеют тенденцию объединяться в цепочки.
   
2. Полная связь (расстояние наиболее удаленных соседей)
   В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т. е. наиболее удаленными соседями). Этот метод обычно работает очень хорошо, когда объекты происходят из отдельных групп. Если же кластеры имеют удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.
   
3. Невзвешенное попарное среднее
   В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных («цепочечного» типа) кластеров.
   
4. Взвешенное попарное среднее
   Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому данный метод должен быть использован, когда предполагаются неравные размеры кластеров.
   
5. Невзвешенный центроидный метод
   В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.
   
6. Взвешенный центроидный метод (медиана)
   Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учета разницы между размерами кластеров. Поэтому, если имеются или подозреваются значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
   

Обзор алгоритмов

Алгоритмы иерархической кластеризации

Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры. Более распространены восходящие алгоритмы, которые в начале работы помещают каждый объект в отдельный кластер, а затем объединяют кластеры во все более крупные, пока все объекты выборки не будут содержаться в одном кластере. Таким образом строится система вложенных разбиений. Результаты таких алгоритмов обычно представляют в виде дерева – дендрограммы. Классический пример такого дерева – классификация животных и растений.

Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью (см. обзор мер расстояний между кластерами).

К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.

Алгоритмы квадратичной ошибки

Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:

где c_j — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).

Алгоритмы квадратичной ошибки относятся к типу плоских алгоритмов. Самым распространенным алгоритмом этой категории является метод k-средних. Этот алгоритм строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:

1. Случайно выбрать k точек, являющихся начальными «центрами масс» кластеров.
2. Отнести каждый объект к кластеру с ближайшим «центром масс».
3. Пересчитать «центры масс» кластеров согласно их текущему составу.
4. Если критерий остановки алгоритма не удовлетворен, вернуться к п. 2.

В качестве критерия остановки работы алгоритма обычно выбирают минимальное изменение среднеквадратической ошибки. Так же возможно останавливать работу алгоритма, если на шаге 2 не было объектов, переместившихся из кластера в кластер.

К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.

Нечеткие алгоритмы

Наиболее популярным алгоритмом нечеткой кластеризации является алгоритм c-средних (c-means). Он представляет собой модификацию метода k-средних. Шаги работы алгоритма:

1. Выбрать начальное нечеткое разбиение n объектов на k кластеров путем выбора матрицы принадлежности U размера n x k.
2. Используя матрицу U, найти значение критерия нечеткой ошибки:
   ,
   где c_k — «центр масс» нечеткого кластера k:
   .
3. Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
4. Возвращаться в п. 2 до тех пор, пока изменения матрицы U не станут незначительными.

Этот алгоритм может не подойти, если заранее неизвестно число кластеров, либо необходимо однозначно отнести каждый объект к одному кластеру.

Алгоритмы, основанные на теории графов

Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа G=(V, E), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность вносения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации.

Алгоритм выделения связных компонент

В алгоритме выделения связных компонент задается входной параметр R и в графе удаляются все ребра, для которых «расстояния» больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры.

Для подбора параметра R обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика – один соответствует внутрикластерным расстояниям, второй – межкластерным расстояния. Параметр R подбирается из зоны минимума между этими пиками. При этом управлять количеством кластеров при помощи порога расстояния довольно затруднительно.

Алгоритм минимального покрывающего дерева

Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом. На рисунке изображено минимальное покрывающее дерево, полученное для девяти объектов.

Путём удаления связи, помеченной CD, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: {A, B, C} и {D, E, F, G, H, I}. Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра EF, которое имеет длину, равную 4,5 единицам.

Послойная кластеризация

Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния c. Например, если расстояние между объектами , то .

Алгоритм послойной кластеризации формирует последовательность подграфов графа G, которые отражают иерархические связи между кластерами:

,

где G^t = (V, E^t) — граф на уровне с^t,
,
с^t – t-ый порог расстояния,
m – количество уровней иерархии,
G⁰ = (V, o), o – пустое множество ребер графа, получаемое при t⁰ = 1,
G^m = G, то есть граф объектов без ограничений на расстояние (длину ребер графа), поскольку t^m = 1.

Посредством изменения порогов расстояния {с⁰, …, с^m}, где 0 = с⁰ < с¹ < …< с^m = 1, возможно контролировать глубину иерархии получаемых кластеров. Таким образом, алгоритм послойной кластеризации способен создавать как плоское разбиение данных, так и иерархическое.

Сравнение алгоритмов

Вычислительная сложность алгоритмов

Алгоритм кластеризации	Вычислительная сложность
Иерархический	O(n2)
k-средних	O(nkl), где k – число кластеров, l – число итераций
c-средних
Выделение связных компонент	зависит от алгоритма
Минимальное покрывающее дерево	O(n2 log n)
Послойная кластеризация	O(max(n, m)), где m < n(n-1)/2

Сравнительная таблица алгоритмов

Алгоритм кластеризации	Форма кластеров	Входные данные	Результаты
Иерархический	Произвольная	Число кластеров или порог расстояния для усечения иерархии	Бинарное дерево кластеров
k-средних	Гиперсфера	Число кластеров	Центры кластеров
c-средних	Гиперсфера	Число кластеров, степень нечеткости	Центры кластеров, матрица принадлежности
Выделение связных компонент	Произвольная	Порог расстояния R	Древовидная структура кластеров
Минимальное покрывающее дерево	Произвольная	Число кластеров или порог расстояния для удаления ребер	Древовидная структура кластеров
Послойная кластеризация	Произвольная	Последовательность порогов расстояния	Древовидная структура кластеров с разными уровнями иерархии

Немного о применении

В своей работе мне нужно было из иерархических структур (деревьев) выделять отдельные области. Т.е. по сути необходимо было разрезать исходное дерево на несколько более мелких деревьев. Поскольку ориентированное дерево – это частный случай графа, то естественным образом подходят алгоритмы, основанными на теории графов.

В отличие от полносвязного графа, в ориентированном дереве не все вершины соединены ребрами, при этом общее количество ребер равно n–1, где n – число вершин. Т.е. применительно к узлам дерева, работа алгоритма выделения связных компонент упростится, поскольку удаление любого количества ребер «развалит» дерево на связные компоненты (отдельные деревья). Алгоритм минимального покрывающего дерева в данном случае будет совпадать с алгоритмом выделения связных компонент – путем удаления самых длинных ребер исходное дерево разбивается на несколько деревьев. При этом очевидно, что фаза построения самого минимального покрывающего дерева пропускается.

В случае использования других алгоритмов в них пришлось бы отдельно учитывать наличие связей между объектами, что усложняет алгоритм.

Отдельно хочу сказать, что для достижения наилучшего результата необходимо экспериментировать с выбором мер расстояний, а иногда даже менять алгоритм. Никакого единого решения не существует.

Список литературы

1. Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. Курс лекций. МГУ, 2007.
2. Jain A., Murty M., Flynn P. Data Clustering: A Review. // ACM Computing Surveys. 1999. Vol. 31, no. 3.
3. Котов А., Красильников Н. Кластеризация данных. 2006.
3. Мандель И. Д. Кластерный анализ. — М.: Финансы и Статистика, 1988.
4. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989.
5. Информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных — www.machinelearning.ru
6. Чубукова И.А. Курс лекций «Data Mining», Интернет-университет информационных технологий — www. intuit.ru/department/database/datamining

Кластеризация в машинном обучении — GeeksforGeeks

Введение в кластеризацию

В основном это тип метода обучения без учителя . Метод обучения без учителя — это метод, в котором мы получаем ссылки из наборов данных, состоящих из входных данных без помеченных ответов. Как правило, он используется как процесс для поиска значимой структуры, объяснительных основных процессов, порождающих функций и группировок, присущих набору примеров.

Кластеризация — это задача разделения совокупности или точек данных на ряд групп таким образом, чтобы точки данных в одних и тех же группах были более похожи на другие точки данных в той же группе и отличались от точек данных в других группах. Это в основном совокупность объектов на основе сходства и несходства между ними.

Например, — точки данных на графике ниже, сгруппированные вместе, могут быть отнесены к одной группе. Мы можем различить кластеры, и мы можем определить, что на изображении ниже есть 3 кластера.

Кластеры не обязательно должны быть сферическими. Например:

DBSCAN: пространственная кластеризация приложений с шумом на основе плотности  
Эти точки данных группируются с использованием базовой концепции, согласно которой точка данных находится в пределах заданного ограничения от центра кластера. Для расчета выбросов используются различные дистанционные методы и методы.

Зачем нужна кластеризация?  
Кластеризация очень важна, поскольку она определяет внутреннюю группировку среди присутствующих неразмеченных данных. Критериев хорошей кластеризации нет. От пользователя зависит, какие критерии он может использовать для удовлетворения своих потребностей. Например, нас может интересовать поиск представителей для однородных групп (редукция данных), поиск «естественных кластеров» и описание их неизвестных свойств («естественные» типы данных), поиск полезных и подходящих группировок («полезные» классы данных). или при обнаружении необычных объектов данных (обнаружение выбросов). Этот алгоритм должен делать некоторые предположения, которые составляют сходство точек, и каждое предположение создает разные и одинаково достоверные кластеры.

Методы кластеризации:  

• Методы на основе плотности: Эти методы рассматривают кластеры как плотную область, имеющую некоторые сходства и отличия от более низкой плотной области пространства. Эти методы обладают хорошей точностью и возможностью объединения двух кластеров. Пример DBSCAN (Пространственная кластеризация приложений с шумом на основе плотности) , OPTICS (Точки заказа для определения структуры кластеризации) и т. д.
• Иерархические методы: Кластеры, сформированные этим методом, образуют древовидную структуру на основе иерархии. Новые кластеры формируются с использованием ранее сформированного. Он разделен на две категории
  • Агломеративные (снизу вверх Подход )
  • Разделительные (сверху вниз подход )

Примеры (кластера с использованием представителей Сокращение кластеризации и использование иерархий) и т. д.

• Методы разделения: Эти методы разбивают объекты на k кластеров, и каждый раздел образует один кластер. Этот метод используется для оптимизации функции подобия объективного критерия, например, когда расстояние является основным параметром. Пример K-средних, CLARANS (кластеризация крупных приложений на основе случайного поиска) и т. д.
• Методы на основе сетки: In В этом методе пространство данных разбивается на конечное число ячеек, образующих структуру, подобную сетке. Все операции кластеризации, выполняемые в этих сетках, выполняются быстро и не зависят от количества объектов данных, пример 9.0007 STING (статистическая информационная сетка), кластер волн, CLIQUE (кластеризация в поисках) и т. д.

Алгоритмы кластеризации:  
Алгоритм кластеризации K-средних — это простейший алгоритм обучения без учителя, который решает проблему кластеризации. означает, что алгоритм разбивает n наблюдений на k кластеров, где каждое наблюдение принадлежит кластеру с ближайшим средним значением, служащим прототипом кластера.

Применение кластеризации в различных областях   

• Маркетинг: Его можно использовать для характеристики и выявления сегментов клиентов в маркетинговых целях.
• Биология: Может использоваться для классификации различных видов растений и животных.
• Библиотеки: Используется для группирования различных книг по темам и информации.
• Страховка: Используется для подтверждения клиентов, их полисов и выявления мошенничества.

Градостроительство: Используется для создания групп домов и изучения их стоимости в зависимости от их географического положения и других факторов.

Исследования землетрясений: Изучив районы, пострадавшие от землетрясения, мы можем определить опасные зоны.

Ссылки:
Wiki
Иерархическая кластеризация
Ijarcs
matteucc
analyticsvidhya
knowm

Кластеризация в машинном обучении — Javatpoint

следующий → ← предыдущая Кластеризация или кластерный анализ — это метод машинного обучения, который группирует немаркированный набор данных. Его можно определить как «Способ группировки точек данных в разные кластеры, состоящие из похожих точек данных. Объекты с возможным сходством остаются в группе, которая имеет меньше или совсем не имеет сходства с другой группой». Он делает это, находя в немаркированном наборе данных некоторые похожие шаблоны, такие как форма, размер, цвет, поведение и т. д., и разделяет их в соответствии с наличием и отсутствием этих похожих шаблонов. Это метод обучения без учителя, поэтому алгоритм не контролируется и работает с немаркированным набором данных. После применения этого метода кластеризации каждому кластеру или группе присваивается идентификатор кластера. Система машинного обучения может использовать этот идентификатор для упрощения обработки больших и сложных наборов данных. Метод кластеризации обычно используется для статистического анализа данных. Примечание. Кластеризация чем-то похожа на алгоритм классификации, но разница заключается в типе набора данных, который мы используем. При классификации мы работаем с помеченным набором данных, тогда как при кластеризации мы работаем с неразмеченным набором данных. Пример : Давайте разберемся с техникой кластеризации на реальном примере торгового центра: когда мы посещаем любой торговый центр, мы можем наблюдать, что вещи с одинаковым использованием сгруппированы вместе. Например, футболки сгруппированы в одну секцию, а брюки — в другие секции, точно так же в овощные секции яблоки, бананы, манго и т. Д. Сгруппированы в отдельные секции, чтобы мы могли легко найти вещи. Точно так же работает и метод кластеризации. Другими примерами кластеризации являются группировка документов по теме. Технику кластеризации можно широко использовать в различных задачах. Некоторые наиболее распространенные варианты использования этой техники: Сегментация рынка Статистический анализ данных Анализ социальных сетей Сегментация изображения Обнаружение аномалий и т. д. Помимо этих общих применений, он используется Amazon в своей системе рекомендаций для предоставления рекомендаций в соответствии с прошлым поиском продуктов. Netflix также использует эту технику, чтобы рекомендовать фильмы и веб-сериалы своим пользователям в соответствии с историей просмотра. На приведенной ниже диаграмме поясняется работа алгоритма кластеризации. Мы видим, что разные фрукты делятся на несколько групп со схожими свойствами. Типы методов кластеризации Методы кластеризации в целом делятся на Жесткая кластеризация (точка данных принадлежит только к одной группе) и Мягкая кластеризация (точки данных могут также принадлежать к другой группе). Но существуют и другие различные подходы кластеризации. Ниже приведены основные методы кластеризации, используемые в машинном обучении: Разделение Кластеризация Кластеризация на основе плотности Кластеризация на основе модели распределения Иерархическая кластеризация Нечеткая кластеризация Разделение Кластеризация Это тип кластеризации, который делит данные на неиерархические группы. Он также известен как метод на основе центроида . Наиболее распространенным примером кластеризации разделов является Алгоритм кластеризации K-средних . В этом типе набор данных разделен на набор из k групп, где K используется для определения количества предопределенных групп. Центр кластера создается таким образом, чтобы расстояние между точками данных одного кластера было минимальным по сравнению с центроидом другого кластера. Кластеризация на основе плотности Метод кластеризации на основе плотности соединяет области с высокой плотностью в кластеры, и распределения произвольной формы формируются до тех пор, пока плотная область может быть соединена. Этот алгоритм делает это, идентифицируя различные кластеры в наборе данных и соединяя области с высокой плотностью в кластеры. Плотные области в пространстве данных отделены друг от друга более разреженными областями. Эти алгоритмы могут столкнуться с трудностями при кластеризации точек данных, если набор данных имеет разную плотность и большую размерность. Кластеризация на основе модели распределения В методе кластеризации на основе модели распределения данные разделяются на основе вероятности принадлежности набора данных к определенному распределению. Группировка выполняется путем предположения о некоторых распределениях, обычно Распределение Гаусса . Примером этого типа является Алгоритм кластеризации максимизации ожидания , в котором используются модели гауссовских смесей (GMM). Иерархическая кластеризация Иерархическая кластеризация может использоваться в качестве альтернативы секционированной кластеризации, поскольку не требуется предварительно указывать количество создаваемых кластеров. В этом методе набор данных делится на кластеры для создания древовидной структуры, которую также называют дендрограммой . Наблюдения или любое количество кластеров можно выбрать, разрезав дерево на нужном уровне. Наиболее распространенным примером этого метода является Агломеративный иерархический алгоритм . Нечеткая кластеризация Нечеткая кластеризация — это тип мягкого метода, при котором объект данных может принадлежать более чем одной группе или кластеру. Каждый набор данных имеет набор коэффициентов принадлежности, которые зависят от степени принадлежности к кластеру. Алгоритм нечетких C-средних является примером такого типа кластеризации; иногда его также называют алгоритмом нечетких k-средних. Алгоритмы кластеризации Алгоритмы кластеризации можно разделить на основе их моделей, описанных выше. Опубликованы различные типы алгоритмов кластеризации, но широко используются лишь некоторые из них. Алгоритм кластеризации основан на типе данных, которые мы используем. Например, некоторые алгоритмы должны угадывать количество кластеров в данном наборе данных, тогда как некоторые должны найти минимальное расстояние между наблюдениями за набором данных. Здесь мы обсуждаем в основном популярные алгоритмы кластеризации, которые широко используются в машинном обучении: Алгоритм K-средних: Алгоритм k-средних является одним из самых популярных алгоритмов кластеризации. Он классифицирует набор данных, разделяя выборки на разные кластеры с одинаковыми отклонениями. В этом алгоритме необходимо указать количество кластеров. Это быстро с меньшим количеством необходимых вычислений, с линейной сложностью O (n). Алгоритм среднего сдвига: Алгоритм среднего сдвига пытается найти плотные области в гладкой плотности точек данных. Это пример модели на основе центроида, которая работает над обновлением кандидатов на центроид, чтобы он стал центром точек в заданной области. Алгоритм DBSCAN: Обозначает для пространственной кластеризации приложений на основе плотности с шумом . Это пример модели на основе плотности, аналогичной модели среднего сдвига, но с некоторыми замечательными преимуществами. В этом алгоритме области с высокой плотностью отделяются от областей с низкой плотностью. Из-за этого кластеры могут быть найдены в любой произвольной форме. Кластеризация с максимизацией ожидания с использованием GMM: Этот алгоритм можно использовать в качестве альтернативы алгоритму k-средних или в тех случаях, когда K-средние могут не сработать. В GMM предполагается, что точки данных распределены по Гауссу. Агломеративный иерархический алгоритм: Агломеративный иерархический алгоритм выполняет восходящую иерархическую кластеризацию. При этом каждая точка данных сначала рассматривается как отдельный кластер, а затем последовательно объединяется. Иерархию кластера можно представить в виде древовидной структуры. Affinity Propagation: Отличается от других алгоритмов кластеризации тем, что не требует указания количества кластеров. При этом каждая точка данных отправляет сообщение между парой точек данных до сходимости. Он имеет O(N 2 T) временная сложность, что является основным недостатком этого алгоритма. Применение кластеризации Ниже приведены некоторые широко известные применения метода кластеризации в машинном обучении: При идентификации раковых клеток: Алгоритмы кластеризации широко используются для идентификации раковых клеток. Он делит наборы данных о раковых и нераковых заболеваниях на разные группы. В поисковых системах: Поисковые системы также работают над техникой кластеризации. Результат поиска отображается на основе ближайшего объекта к поисковому запросу. Он делает это, группируя схожие объекты данных в одну группу, которая находится далеко от других разнородных объектов. Точный результат запроса зависит от качества используемого алгоритма кластеризации. Сегментация клиентов: Используется в исследованиях рынка для сегментации клиентов на основе их выбора и предпочтений. По биологии: Используется в биологии для классификации различных видов растений и животных с использованием техники распознавания изображений. В землепользовании: Техника кластеризации используется для определения площади аналогичного землепользования в базе данных ГИС. Это может быть очень полезно, чтобы выяснить, для какой цели следует использовать конкретную землю, а значит, для какой цели она больше подходит. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт