Алгоритм Denso И Yazaki И Др — Одометры

Вот что пишут к примеру

Как пересчитать пробег в спидометрах TOYOTA DENSO. Кодировка пробега.

Рассмотрим алгоритм пересчета пробега в спидометрах с EEPROM, 93с46, 93с56, 93с66, 93A57, и их модификаций. Данный алгоритм очень прост, и применяется на большинстве автомобилей TOYOTA, а так же других японских и корейских автомобилях. В основном это спидометры DENSO. Начиная с 2006 года, TOYOTA немного видоизменила алгоритм пересчета пробега. Изменились адреса, а так же по-другому стали пересчитываться младшие цифры пробега.

Старый тип спидометров (тип 1).

Пробег в этих спидометрах занимает 3 байта+1 пустой байт, и повторяется в дампе 3 раза.
Первый 08h,09h,0Ah,0Bh.
Второй 0Ch,0Dh,0Eh,0Fh.
Третий 10h,11h,12h,13h.
По адресам 0Bh, 0Fh, 13h. В левом полубайте находятся сотни тысяч пробега, в правом полубайте десятки тысяч пробега. По адресам 08h, 0Ch, 10h. В левом полубайте находятся единицы тысяч пробега, а в правом сотни километров. По адресам 09h, 0Dh, 11h. В левом полубайте находятся десятки километров пробега, а в правом единицы километров пробега. Каждая цифра пробега хранится в инверсном виде. Например, цифра 1 будет преобразована в E, а 5 в A. Это можно записать в виде выражения (ПРОБЕГ НА ОДОМЕТРЕ) NOT=(ПРОБЕГ В ПАМЯТИ). Здесь операция NOT, это инверсия. Ещё можно записать так, 0Fh-(ПРОБЕГ НА ОДОМЕТРЕ)= ПРОБЕГ В ПАМЯТИ.

Новый тип спидометров (тип 2).

Здесь пробег шифруется таким же образом. По адресам, первый 62h, 63h, 64h, 65h, второй 66h, 67h, 68h, 69h, третий 6Ah, 6Bh, 6Ch, 6Dh. Цифры кодируются точно так же, за исключением десятков и единиц километража пробега. Здесь байты 63h, 67h, 6Bh показывают, 0 километров или 50 километров. А в верхней части EEPROM, выделен участок в 50 байт, который изначально заполнен значением FFh. Затем каждый километр спидометр записывает маркер на ближайший к началу и свободный ( без маркера ) байт. Так продолжается пока не заполнятся все 50 байт. Далее спидометр очищает все 50 байт массива, и записывает значение 50 километров в ячейки 63h, 67h, 6Bh. Далее процесс повторяется.

Опубликована база с 320 млн уникальных паролей (5,5 ГБ) / Habr

Проверка аккаунтов на живучесть

Одно из главных правил при выборе пароля — не использовать пароль, который уже засветился в каком-нибудь взломе и попал в одну из баз, доступных злоумышленникам. Даже если в вашем пароле 100500 символов, но он есть там — дело плохо. Например, потому что в программу для брутфорса паролей можно загрузить эту базу как словарный список. Как думаете, какой процент хешей она взломает, просто проверив весь словарный список? Вероятно, около 75% (реальную статистику см. ниже).

Так вот, откуда нам знать, какие пароли есть у злоумышленников? Благодаря специалисту по безопасности Трою Ханту можно проверить эти базы. Более того, их можно скачать к себе на компьютер и использовать для своих нужд. Это два текстовых файла в архивах: с 306 млн паролей (5,3 ГБ) и с 14 млн паролей (250 МБ).

Базы лежат на этой странице.

Все пароли в базе представлены в виде хешей SHA1. Перед хешированием все символы переведены в верхний регистр (прописные буквы). Трой Хант говорит, что применил функцию HASHBYTES, которая переводит хеши в верхний регистр. Так что делая свой хеш, следует осуществить аналогичную процедуру, если хотите найти совпадение.

Прямые ссылки:

https://downloads.pwnedpasswords.com/passwords/pwned-passwords-1.0.txt.7z
(306 млн паролей, 5,3 ГБ), зеркало
SHA1 hash of the 7-Zip file: 90d57d16a2dfe00de6cc58d0fa7882229ace4a53
SHA1 hash of the text file: d3f3ba6d05b9b451c2b59fd857d94ea421001b16

В разархивированном виде текстовый файл занимает 11,9 ГБ.

https://downloads.pwnedpasswords.com/passwords/pwned-passwords-update-1.txt.7z
(14 млн паролей, 250 МБ), зеркало
SHA1 hash of the 7-Zip file: 00fc585efad08a4b6323f8e4196aae9207f8b09f
SHA1 hash of the text file: 3fe6457fa8be6da10191bffa0f4cec43603a9f56

Если вы глупы бесстрашны, то на той же странице можете ввести свой уникальный пароль и проверить его на наличие в базах, не скачивая их. Трой Хант обещает, что никак не будет использовать ваш пароль и его сервис абсолютно надёжен. «Не отправляйте свой активно используемый пароль ни на какой сервис — даже на этот!», — предупреждается на странице. Программные интерфейсы этого сервиса полностью документированы, они принимают хеши SHA1 примерно таким образом:

GET https://haveibeenpwned.com/api/v2/pwnedpassword/ce0b2b771f7d468c0141918daea704e0e5ad45db?originalPasswordIsAHash=true

Но всё равно надёжнее проверять свой пароль в офлайне. Поэтому Трой Хант выложил базы в открытый доступ на дешёвом хостинге. Он отказался сидировать торрент, потому что это «затруднит доступ людей к информации» — многие организации блокируют торренты, а для него небольшие деньги за хостинг ничего не значат.

Хант рассказывает, где он раздобыл эти базы. Он говорит, что источников было много. Например, база Exploit.in содержит 805 499 391 адресов электронной почты с паролями. Задачей Ханта было извлечение уникальных паролей, поэтому он сразу начал анализ на совпадения. Оказалось, что в базе всего лишь 593 427 119 уникальных адресов и лишь 197 602 390 уникальных паролей. Это типичный результат: абсолютное большинство паролей (в данном случае, 75%) не уникальны и используются многими людьми. Собственно, поэтому и даётся рекомендация после генерации своего мастер-пароля сверять его по базе.

Вторым по величине источником информации был Anti Public: 562 077 488 строк, 457 962 538 уникальных почтовых адресов и ещё 96 684 629 уникальных паролей, которых не было в базе Exploit.in.

Остальные источники Трой Хант не называет, но в итоге у него получилось 306 259 512 уникальных паролей. На следующий день он добавил ещё 13 675 934, опять из неизвестного источника — эти пароли распространяются отдельным файлом.

Так что сейчас общее число паролей составляет 319 935 446 штук. Это по-настоящему уникальные пароли, которые прошли дедупликацию. Из нескольких версий пароля (P@55w0rd и p@55w0rd) в базу добавляется только одна (p@55w0rd).

После того, как Трой Хант спросил в твиттере, какой дешёвый хостинг ему могут посоветовать, на него вышла известная организация Cloudflare и предложила захостить файлы забесплатно. Трой согласился. Так что смело качайте файлы с хостинга, это бесплатно для автора.

Про алгоритмы для новичков

Если вы когда-либо слышали, что алгоритмы нужно знать всем разработчикам, но что это такое представляете с трудом – вам сюда.

Для опытных программистов некоторые понятия, в том числе и алгоритмы, настолько фундаментальны, что не возникает даже мыслей о том, что, то или иное определение может оказаться непонятным, сложным или вообще, пугающим, для новичка.

Алгоритм – вызывает ассоциации ни то с логарифмами, ни то с арифметикой.

И это слово действительно пришло из математики и использовалось для описания алгоритма Евклида, который применяется для нахождения наибольшего общего делителя двух целых чисел.

Если говорить нормальным языком, алгоритм – это пошаговая инструкция, где результат прошлого шага строго определен и используется в качестве входных данных для следующего шага.

Однако, поскольку в реальной жизни при написании программы совсем нечасто нужно искать общий делитель у целых чисел, раскладывать на множители и вообще думать о математиках, творивших в 300-е года до н.э., рассмотрим немного более жизненный пример применения алгоритмов.

Давайте представим, что телефонный справочник все еще актуален (да, тот бумажный, если вы их застали). Допустим, мы хотим набрать Николая Должанского. Принимая во внимание, что Николай есть в телефонном справочнике, мы можем найти его номер несколькими различными способами.

Самый простой способ найти что-то в списке – пройти по нему по порядку, сравнивая с искомым значением. То есть:

1. Надежда Александрова –> не подходит

2. Николай Алексеев –> не подходит

…

И так далее, пока вы не найдете наконец Николая Должанского. Вероятно, понадобятся десятки и даже сотни операций сравнения. То есть, если вы захотите поболтать с Ярославом Яковлевым, то это займет порядком больше времени.

Как вы уже поняли, смысл алгоритма линейного поиска заключается в простом переборе значений от начала списка и до конца (или искомого результата). Это брутфорс. Этот алгоритм крайне прост и может возникнуть множество ситуаций, где его использование будет иметь смысл.

Например, если нужно найти телефон приятеля не в целой книге, а, предположим, на клочке бумаги, где помимо его номера всего десяток других записей – пройти список сверху вниз, в этом случае, будет умным решением.

У большинства людей просто не хватит терпения перебирать весь справочник. Поэтому они пойдут более прагматичным путем – будут разделять книгу на части.

Процесс деления на части предполагает сначала нахождение основной области, где, предположительно, находится искомое значение. Мы тут все еще ищем Николая Должанского.

Поиск начнем, перелистнув книгу на 30 страниц вперед. Мы увидим, что все фамилии начинаются на «Б». Перейдем еще на 60 вперед и увидим «Г». Достоверно известно, что «Г» находится прямо перед «Д», а значит, Коля где-то рядом и с этого момента мы будем двигаться осторожнее.

Этот алгоритм описывает, как большинство людей ищут что-то в справочниках. Но поскольку мы, люди, часто выбираем неоптимальные пути решения задач, рассмотрим правильный подход к делению на части – бинарный алгоритм поиска.

Вот это уже звучит серьезно, да? На самом деле, ничего сложного. Бинарный поиск предполагает, что мы будем делить исходный массив данных пополам, отбрасывать ту часть, где искомого значения быть не может и делить остаток пополам снова, пока область поиска не сократится до минимально возможной.

В терминах телефонной книги, работа будет строиться следующим образом. Наш справочник содержит 400 страниц. Даже если мы все еще ищем Николая Должанского, который находится на 136 странице, мы можем воспользоваться бинарным поиском. Делим книгу пополам и по счастливой случайности попадаем прямо между буквами «М» и «Н» на 199 и 200 страницах соответственно. Мы знаем, что буква «Д» в алфавите находится перед «М», так что справедливо будет утверждение:

Николай Должанский находится на странице между 0 и 199

Ту часть, что начинается с «Н» мы выбрасываем.

Далее, мы делим на две части первые 200 страниц телефонного справочника и видим, что попали мы прямо на страницу с буквой «Г», а «Г», как известно, идет перед «Д». То есть нам снова стал известен неоспоримый факт:

Телефон Николая Должанского находится между 99 и 199 страницами

И вот, стартовав с 400 страниц, мы, всего через две операции сравнения, сократили область поиска на 3/4. Учитывая, что телефон Коли находится на 136 странице, нам предстоит сделать следующие операции:

[99-199] -> [99-149] -> [124-149] -> [124-137] -> [130-137] -> [133-137] -> [135-137] -> [136]

Еще 6 сравнений. Чтобы рассчитать количество операций необходимых для нахождения нужной страницы бинарным поиском, мы можем взять логарифм от количества страниц с основанием 2 и получим:

log2(400) = 8.644

то есть, округлив, в худшем случае – 9 операций сравнения. Рядом с исходным числом страниц, конечно, ерунда. Но давайте поговорим о по-настоящему серьезных книгах. Пусть в нашем справочнике будет не 400, а 4 000 000 страниц. Попробуйте представить, сколько операций сравнения нам потребуется? На самом деле, немного:

log2(4000000) = 21.932

то есть, 22 раза нужно будет провести сравнение частей справочника, прежде, чем 4 000 000 превратятся в 1.

Сравните скорость работы линейного и бинарного алгоритмов поиска для такого количества страниц.

В общем, так и со всеми алгоритмами. Изучение алгоритмов – это изучение способов решать проблемы и задачи наиболее оптимальным путем. Алгоритм – это решение, рассмотренное со всех сторон и преобразованное в эдакий todo-list действий, которые нужно совершить, чтобы воспроизвести его.

И отдельная тема, это преобразование алгоритма в код на конкретном языке, ведь в разных языках алгоритмы (особенно поисковые) могут реализовываться по-разному. Иногда, это может быть уже встроенная в язык функция, которая выдаст нужный результат из массива одной строкой, а где-то понадобиться пара-тройка десятков строк.

И, для примера, вот так будет реализован бинарный поиск на Ruby:

def binary_search(target, list)
  position = (list.count / 2).floor
  mid = list[position]

  return mid if mid == target

  if(mid < target)
    return binary_search(target, list.slice(position + 1, list.count/2))
  else
    return binary_search(target, list.slice(0, list.count/2))
  end
end


puts binary_search(9, [1,2,3,4,5,6,7,8,9,10])

Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы

Знай сложности алгоритмов / Habr

Эта статья рассказывает о времени выполнения и о расходе памяти большинства алгоритмов используемых в информатике. В прошлом, когда я готовился к прохождению собеседования я потратил много времени исследуя интернет для поиска информации о лучшем, среднем и худшем случае работы алгоритмов поиска и сортировки, чтобы заданный вопрос на собеседовании не поставил меня в тупик. За последние несколько лет я проходил интервью в нескольких стартапах из Силиконовой долины, а также в некоторых крупных компаниях таких как Yahoo, eBay, LinkedIn и Google и каждый раз, когда я готовился к интервью, я подумал: «Почему никто не создал хорошую шпаргалку по асимптотической сложности алгоритмов? ». Чтобы сохранить ваше время я создал такую шпаргалку. Наслаждайтесь!

Поиск

Сортировка

Структуры данных

Кучи

Представление графов

Пусть дан граф с |V| вершинами и |E| ребрами, тогда

Нотация асимптотического роста

1. (О — большое) — верхняя граница, в то время как (Омега — большое) — нижняя граница. Тета требует как (О — большое), так и (Омега — большое), поэтому она является точной оценкой (она должна быть ограничена как сверху, так и снизу). К примеру, алгоритм требующий Ω (n logn) требует не менее n logn времени, но верхняя граница не известна. Алгоритм требующий Θ (n logn) предпочтительнее потому, что он требует не менее n logn (Ω (n logn)) и не более чем n logn (O(n logn)).
2. f(x)=Θ(g(n)) означает, что f растет так же как и g когда n стремится к бесконечности. Другими словами, скорость роста f(x) асимптотически пропорциональна скорости роста g(n).
3. f(x)=O(g(n)). Здесь темпы роста не быстрее, чем g (n). O большое является наиболее полезной, поскольку представляет наихудший случай.

Короче говоря, если алгоритм имеет сложность __ тогда его эффективность __

График роста O — большое

Наивный Байесовский классификатор в 25 строк кода / Habr

Наивный Байесовский классификатор один из самых простых из алгоритмов классификации. Тем не менее, очень часто он работает не хуже, а то и лучше более сложных алгоритмов. Здесь я хочу поделиться кодом и описанием того, как это все работает.

И так, для примера возьму задачу определения пола по имени. Конечно, чтобы определить пол можно создать большой список имен с метками пола. Но этот список в любом случае будет неполон. Для того чтобы решить эту проблему, можно «натренировать» модель по маркированным именам.
Если интересует, прошу .

Немного теории

Пусть у нас есть строка текста O. Кроме того, имеются классы С, к одному из которых мы должны отнести строку. Нам необходимо найти такой класс с, при котором его вероятность для данной строки была бы максимальна. Математически это записывается так:

Вычислить P(C|O) сложно. Но можно воспользоваться теоремой Байеса и перейти к косвенным вероятностям:

Так как мы ищем максимум от функции, то знаменатель нас не интересует (он в данном случае константа). Кроме того, нужно взглянуть на строку O. Обычно, нет смысла работать со всей строкой. Намного эффективней выделить из нее определенные признаки (features). Таким образом формула примет вид:

Знаменатель нас не интересует. Числитель же можно переписать так.

Но это опять сложно. Здесь включаем «наивное» предположение о том, что переменные O зависят только от класса C, и не зависят друг от друга. Это сильно упрощение, но зачастую это работает. Числитель примет вид:

Финальная формула примет вид:

(1)

Т.е. все что нужно сделать, это вычислить вероятности P( C ) и P(O|C). Вычисление этих параметров и называется тренировкой классификатора.

Код

Ниже — код на питоне. Содержит всего две функции: одна для тренировки (подсчета параметров формулы), другая для классификации (непосредственный расчет формулы).

from __future__ import division
from collections import defaultdict
from math import log

def train(samples):
    classes, freq = defaultdict(lambda:0), defaultdict(lambda:0)
    for feats, label in samples:
        classes[label] += 1                 # count classes frequencies
        for feat in feats:
            freq[label, feat] += 1          # count features frequencies

    for label, feat in freq:                # normalize features frequencies
        freq[label, feat] /= classes[label]
    for c in classes:                       # normalize classes frequencies
        classes[c] /= len(samples)

    return classes, freq                    # return P(C) and P(O|C)

def classify(classifier, feats):
    classes, prob = classifier
    return min(classes.keys(),              # calculate argmin(-log(C|O))
        key = lambda cl: -log(classes[cl]) + \
            sum(-log(prob.get((cl,feat), 10**(-7))) for feat in feats))

В функции train первые пять строк производят подсчет количества классов C, а также частоту появления фич O и С в одном семпле. Вторая часть метода просто нормирует эти частоты. Таким образом на выходе получаются вероятности P© и P(O|C).

В функции classify происходит поиск наиболее вероятного класса. Единственное отличие от формулы (1) в том, что я заменяю произведение вероятностей на сумму логарифмов, взятых с отрицательным знаком, и вычисляю не argmax, а argmin. Переход к логарифмам — распространненный прием чтобы избежать слишком маленьких чисел, которые могли бы получится при произведении вероятностей.
Число 10(^-7), которое подставляется в логарифм, это способ избежать нуля в аргументе логарифма (т.к. он будет иначе он будет неопределен).

Чтобы натренировать классификатор возьмем размеченный список мужских и женских имен и воспользуемся этим кодом:

def get_features(sample): return (sample[-1],) # get last letter

samples = (line.decode('utf-8').split() for line in open('names.txt'))
features = [(get_features(feat), label) for feat, label in samples]
classifier = train(features)

print 'gender: ', classify(classifier, get_features(u'Аглафья'))

Файл ‘names.txt’ можно скачать здесь.

В качестве фич я выбрал последнюю букву имени (см функцию get_features). Работает неплохо, но для рабочего варианта лучше использовать схему посложнее. К примеру, выбрать первую букву имени и две последних. К примеру, вот так:

def get_features(sample): return (
        'll: %s' % sample[-1],          # get last letter
        'fl: %s' % sample[0],           # get first letter
        'sl: %s' % sample[1],           # get second letter
        )

Алгоритм можно использовать для произвольного числа классов. К примеру, можно попробовать построить классификатор текстов по эмоциональной окраске.

Тесты

Я протестировал классификатор на части исходного корпуса с именами. Точность составила 96%. Это не блестящий результат, но для многих задач вполне достаточно.

Элементарные шифры на понятном языке / Habr

Привет, Хабр!

Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.

Прежде всего, разберемся в терминологии.

Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.

Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.

Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.

Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.

Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.

Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.

Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.

Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.

Например, есть у нас алфавит, который полностью соответствует обычной латинице.

a b c d e f g h i j k l m n o p q r s t u v w x y z

Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:

И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра

Исходное сообщение: I love habr
Зашифрованное: r olev szyi

Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.

Опять же, для наглядности, возьмем латиницу

a b c d e f g h i j k l m n o p q r s t u v w x y z

И теперь сместим вправо или влево каждую букву на ключевое число значений.

Например, ключ у нас будет 4 и смещение вправо.

Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v

Пробуем написать сообщение:

hello world

Шифруем его и получаем следующий несвязный текст:

dahhk sknhz

• Шифр Вернама (XOR-шифр)

Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).

Исходный алфавит — все та же латиница.

Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.

Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.

XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.

Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.

Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ

Например:

сообщение: LONDON
ключ: SYSTEM

Переведем их в бинарный код и выполним XOR:

01001100 01001111 01001110 01000100 01001111 01001110
01010011 01011001 01010011 01010100 01000101 01001101
_______________________________________________________
00011111 00010110 00011101 00010000 00001010 00000011

В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:

31 22 29 16 10 3. 

С виду — совершенно несвязный набор чисел, но мы-то знаем.

• Шифр кодового слова

Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.

Например, возьмем для разнообразия, кириллический алфавит.

абвгдеёжзийклмнопрстуфхцчшщъыьэюя

Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».

Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.

абвгдеёжзийклмнопрстуфхцчшщъыьэюя
лукомрьеабвгдёжзийнпстфхцчшщъыэюя

И теперь запишем любое сообщение и зашифруем его.

"Златая цепь на дубе том"

Получим в итоге следующий нечитаемый бред:

"Адлпля хриы жл мсур пиё"

• Шифр Плейфера

Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.

Пусть кодовое слово у нас будет «HELLO».

Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.

Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».

Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.

IL OV EH AB RA ND GI TH UB.

Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.

Шифрование выполняется по нескольким несложным правилам:

1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.

Например, EH становится LE.

2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.

Например, если бы у нас была биграмма LX, то она стала бы DL.

3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.

Например, биграмма RA.

По этим правилам, шифруем все сообщение.

IL OV EH AB RA ND GI TH UB.
KO HY LE HG EU MF BP QO QG

Если убрать пробелы, то получим следующее зашифрованное сообщение:

KOHYLEHGEUMFBPQOQG

Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.

Спасибо за внимание.

RSA — Википедия

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений, включая PGP, S/MIME, TLS/SSL, IPSEC/IKE и других^[3].

Опубликованная в ноябре 1976 года статья Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» (англ. New Directions in Cryptography)^[4] перевернула представление о криптографических системах, заложив основы криптографии с открытым ключом. Разработанный впоследствии алгоритм Диффи — Хеллмана позволял двум сторонам получить общий секретный ключ, используя незащищенный канал связи. Однако этот алгоритм не решал проблему аутентификации. Без дополнительных средств пользователи не могли быть уверены, с кем именно они сгенерировали общий секретный ключ.

Изучив эту статью, трое учёных Рональд Ривест, Ади Шамир и Леонард Адлеман из Массачусетского технологического института (MIT) приступили к поискам математической функции, которая бы позволяла реализовать сформулированную Уитфилдом Диффи и Мартином Хеллманом модель криптографической системы с открытым ключом. После работы над более чем 40 возможными вариантами им удалось найти алгоритм, основанный на различии в том, насколько легко находить большие простые числа и насколько сложно раскладывать на множители произведение двух больших простых чисел, получивший впоследствии название RSA. Система была названа по первым буквам фамилий её создателей.

В августе 1977 года в колонке «Математические игры» Мартина Гарднера в журнале Scientific American, с разрешения Рональда Ривеста^[5] появилось первое описание криптосистемы RSA^[6]. Читателям также было предложено дешифровать английскую фразу, зашифрованную описанным алгоритмом:

9686 1477 8829 7431 0816 3569 8962 1829

9613 1409 0575 9874 2982 3147 8013 9451

7546 2225 9991 6951 2514 6622 3919 5781

2206 4355 1245 2093 5708 8839 9055 5154

В качестве открытых параметров системы были использованы числа n= (129 десятичных знаков, 425 бит, также известно как RSA-129) и e=9007. За расшифровку была обещана награда в 100 долларов США. По заявлению Ривеста, для факторизации числа потребовалось бы более 40 квадриллионов лет^[7][3]. Однако чуть более чем через 15 лет, 3 сентября 1993 года было объявлено о запуске проекта распределённых вычислений с координацией через электронную почту по нахождению сомножителей числа RSA-129 и решению головоломки. На протяжении полугода более 600 добровольцев из 20 стран жертвовали процессорное время 1600 машин (три из которых были факс-машинами^{[источник не указан 1482 дня]}). В результате были найдены простые множители и расшифровано исходное сообщение, которое представляет собой фразу «THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE (англ.)» («Волшебные слова — это брезгливый ягнятник»)^[8][9]. Полученную награду победители пожертвовали в фонд свободного программного обеспечения.

После публикации Мартина Гарднера полное описание новой криптосистемы любой желающий мог получить, выслав по почте запрос Рональду Ривесту с приложенным конвертом с обратным адресом и марками на 35 центов.^[6] Полное описание новой криптосистемы было опубликовано в журнале «Communications of the ACM» в феврале 1978 года^[10].

Заявка на патент была подана 14 декабря 1977 года, в качестве владельца был указан MIT. Патент 4405829 был выдан 20 сентября 1983 года, а 21 сентября 2000 года срок его действия истёк^[11]. Однако за пределами США у изобретателей патента на алгоритм не было, так как в большинстве стран его необходимо было получить до первой публикации^[12].

В 1982 году Ривест, Шамир и Адлеман организовали компанию RSA Data Security (англ.) (в настоящий момент — подразделение EMC). В 1989 году RSA, вместе с симметричным шифром DES, упоминается в RFC 1115, тем самым начиная использование алгоритма в зарождающейся сети Internet^[13], а в 1990 году использовать алгоритм начинает министерство обороны США^[14].

В ноябре 1993 года открыто публикуется версия 1.5 стандарта PKCS1 (англ.), описывающего применение RSA для шифрования и создания электронной подписи. Последние версии стандарта также доступны в виде RFC (RFC 2313 — 1.5, 1993 год; RFC 2437 — 2.0, 1998 год; RFC 3447 — 2.1, 2002 год).

В декабре 1997 года была обнародована информация, согласно которой британский математик Клиффорд Кокс (Clifford Cocks), работавший в центре правительственной связи (GCHQ) Великобритании, описал криптосистему, аналогичную RSA в 1973 году^[15].

Введение[править | править код]

Криптографические системы с открытым ключом используют так называемые односторонние функции, которые обладают следующим свойством:

• если известно x{\displaystyle x}, то f(x){\displaystyle f(x)} вычислить относительно просто;
• если известно y=f(x){\displaystyle y=f(x)}, то для вычисления x{\displaystyle x} нет простого (эффективного) пути.

Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.

В основу криптографической системы с открытым ключом RSA положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители.

В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными, то есть:

∀{\displaystyle \forall } допустимых пар открытого и закрытого ключей (p,s){\displaystyle (p,s)}

∃{\displaystyle \exists } соответствующие функции шифрования Ep(x){\displaystyle E_{p}(x)} и расшифрования Ds(x){\displaystyle D_{s}(x)} такие, что

∀{\displaystyle \forall } сообщения m∈M{\displaystyle m\in M}, где M{\displaystyle M} — множество допустимых сообщений,

m=Ds(Ep(m))=Ep(Ds(m)).{\displaystyle m=D_{s}(E_{p}(m))=E_{p}(D_{s}(m)).}

Алгоритм создания открытого и секретного ключей[править | править код]

RSA-ключи генерируются следующим образом:^[16]

1. Выбираются два различных случайных простых числа p{\displaystyle p} и q{\displaystyle q} заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение n=p⋅q{\displaystyle n=p\cdot q}, которое называется модулем.
3. Вычисляется значение функции Эйлера от числа n{\displaystyle n}:

   φ(n)=(p−1)⋅(q−1).{\displaystyle \varphi (n)=(p-1)\cdot (q-1).}

4. Выбирается целое число e{\displaystyle e} (1<e<φ(n){\displaystyle 1<e<\varphi (n)}), взаимно простое со значением функции φ(n){\displaystyle \varphi (n)}.
   • Число e{\displaystyle e} называется открытой экспонентой (англ. public exponent)
   • Обычно в качестве e{\displaystyle e} берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые из чисел Ферма: 17, 257 или 65537, так как в этом случае время, необходимое для шифрования с использованием быстрого возведения в степень будет меньше.
   • Слишком малые значения e{\displaystyle e}, например 3, потенциально могут ослабить безопасность схемы RSA.^[17]
5. Вычисляется число d{\displaystyle d}, мультипликативно обратное к числу e{\displaystyle e} по модулю φ(n){\displaystyle \varphi (n)}, то есть число, удовлетворяющее сравнению:

   d⋅e≡1(modφ(n)).{\displaystyle d\cdot e\equiv 1{\pmod {\varphi (n)}}.}

6. Пара (e,n){\displaystyle (e,n)} публикуется в качестве открытого ключа RSA (англ. RSA public key).
7. Пара (d,n){\displaystyle (d,n)} играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.

Шифрование и расшифрование[править | править код]

Предположим, Боб хочет послать Алисе сообщение m{\displaystyle m}.

Сообщениями являются целые числа в интервале от 0{\displaystyle 0} до n−1{\displaystyle n-1}, т.е m∈Zn{\displaystyle m\in \mathbb {Z} _{n}}.

Данная схема на практике не используется по причине того, что она не является практически надёжной (semantically secured). Действительно, односторонняя функция E(m) является детерминированной — при одних и тех же значениях входных параметров (ключа и сообщения) выдаёт одинаковый результат. Это значит, что не выполняется необходимое условие практической (семантической) надёжности шифра.

Алгоритм шифрования сеансового ключа[править | править код]

Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается.

Алгоритм шифрования сеансового ключа выглядит следующим образом^[18]:

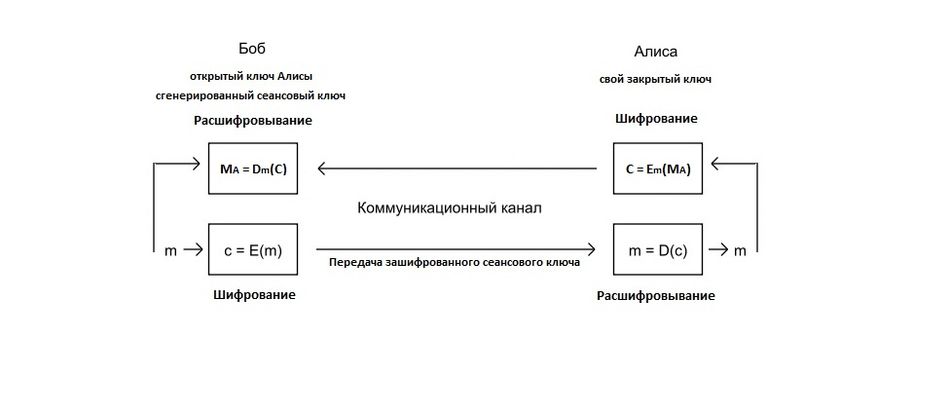
В случае, когда сеансовый ключ больше, чем модуль n{\displaystyle n}, сеансовый ключ разбивают на блоки нужной длины (в случае необходимости дополняют нулями) и шифруют каждый блок.

Корректность схемы RSA[править | править код]

Уравнения (1){\displaystyle (1)} и (2){\displaystyle (2)}, на которых основана схема RSA, определяют взаимно обратные преобразования множества Zn{\displaystyle \mathbb {Z} _{n}}