Частотность поисковых запросов — сервис для определения частотности
Частота ключевых слов и SEO
Если вы пытаетесь занять место по ключевому слову органически , важно знать частоту ваших ключевых слов. Если частота ваших ключевых слов слишком низкая, у вас возникнут проблемы с рейтингом по этому ключевому слову, если только уровень конкуренции не будет очень низким. Поисковые системы, такие как Google, должны видеть «доказательство» в виде ключевых слов, что ваш контент действительно соответствует запросу.
Однако, если частота вашего ключевого слова слишком высока, это посылает негативный сигнал поисковым системам. Избегайте черных методов, известного как «наполнение ключевыми словами», когда частота ваших ключевых слов неестественно высока и отвлекает пользователей.
Как определить частотность
Веб-мастер и SEO-специалист определяет частотность запроса при помощи специализированных сервисов. Например, в Яндексе это Вордстат (читайте, как это сделать в нашей статье).
Если воспользоваться кавычками, перед запросом и после него, то в итоге система выдает данные о частоте, учитывая необходимую последовательность слов. Для получения точных данных по частоте с имеющейся морфологией, перед словом следует ставить «!».
Какая частота ключевых слов считается хорошей?
Новички в SEO и платном поиске часто спрашивают, какая частота ключевых слов «хорошая» или какие рекомендации им следует соблюдать, когда дело доходит до определения правильной плотности ключевых слов. К сожалению, как и в случае со многими элементами SEO и интернет-рекламы, существует несколько настоящих «правил» относительно частоты ключевых слов. Однако есть некоторые общепринятые передовые методы, которым вы, возможно, захотите следовать.
Вообще говоря, многие профессионалы SEO согласны с тем, что ключевое слово не должно появляться чаще одного раза на 200 слов текста. Это означает, что из каждых 200 слов текста на веб-странице данное ключевое слово не должно появляться более одного раза.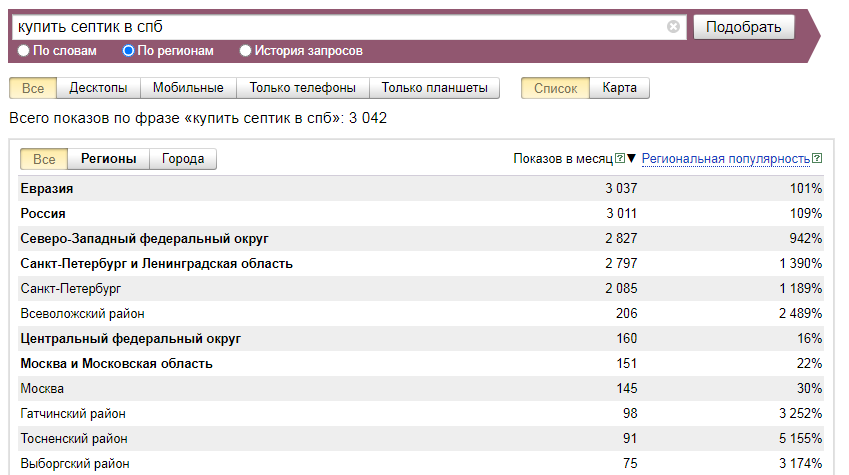
Сюда входят близкие варианты ключевого слова. Например, «подержанные автомобили» — это вариант ключевого слова «подержанные автомобили». Хотя эти два термина различны, они тесно связаны семантически; их значения идентичны, и только их формулировка отличает их друг от друга. Это означает, что вам следует попытаться разделить варианты ключевых слов, как если бы вы использовали несколько экземпляров одного и того же ключевого слова.
Насколько важна частота ключевых слов?
Хотя частота ключевых слов может повлиять на степень обнаружения сайта или веб-страницы, это лишь один из многих таких факторов.
В прошлом многие сайты обходились без «наполнения ключевыми словами» — практики запихивания как можно большего количества ключевых слов и вариантов на одной веб-странице в попытке манипулировать рейтингом страницы. Однако сегодня алгоритмы поиска значительно сложнее, что делает такие методы в значительной степени бесполезными и потенциально даже вредными.
Частота ключевых слов и пользовательский опыт
Возможно, было бы более эффективно думать о частоте ключевых слов не в контексте внутреннего SEO, а скорее в контексте пользовательского опыта.
Независимо от того, какой тип контента содержит веб-страница — список продуктов, сообщение в блоге, целевая страница, страница с благодарностью — всегда учитывайте взаимодействие с пользователем. Все тексты должны читаться легко и естественно, а включение вынужденных, неудобных ключевых слов — один из самых быстрых способов испортить впечатление вашей аудитории.
Заблуждения, связанные с частотностью
Миф первый. Частотность по Wordstat соответствует частоте запросов в поисковой системе Яндекс
Число, которое размещенное напротив определенного запроса, является только предварительным прогнозным значением показов в течение месяца. Точная информация может быть получена исключительно по факту. Для этого необходимо выбрать запрос как ключ и проверить статистику на основании отчетного промежутка времени.
Для получения более точного прогнозного значения необходимо помнить о специализированных операторах – восклицательный знак и кавычки. Также можно указывать регион и использовать прочий инструментарий, предлагаемый сервисом.
Миф второй. Трафик можно предсказывать с помощью информации из Wordstat Результаты экспериментов, которые проводили оптимизаторы, продемонстрировали, что если сайт находится в ТОП-10 по высокочастотному запросу, то это не гарантирует ему трафик.
Миф третий. Информация о частоте запросов из Вордстат позволяет составить семантическое ядро
Информация, предлагаемая данным сервисом, не может считаться полноценным источником формирования семантического ядра для продвижения. Конкурентным и целевым может считаться менее частотный запрос. С помощью таких запросов удается увеличить не только прирост трафика, но и увеличение продаж. Даже если напротив запроса указана цифра 9, то это еще не значит, что данный запрос никто не вводит в строку поиска. Высокочастотный запрос иногда не имеет соответствующего частоте трафикового потенциала.
Анализ рынка и опыт специалиста является залогом успеха.
Частота, таблицы частот и уровни измерения
РЕЗУЛЬТАТЫ обучения
- Создание и интерпретация таблиц частот.
Когда у вас есть набор данных, вам нужно будет организовать его, чтобы вы могли анализировать, как часто каждый элемент данных встречается в наборе. Однако при расчете частоты вам может понадобиться округлить ответы, чтобы они были максимально точными.
Ответы и округление
Простой способ округления ответов состоит в том, чтобы добавить в окончательный ответ еще один десятичный знак по сравнению с исходными данными. Округлите только окончательный ответ. По возможности не округляйте промежуточные результаты. Если возникнет необходимость округлить промежуточные результаты, доведите их как минимум до удвоенного количества знаков после запятой, чем окончательный ответ. Например, среднее из трех оценок викторины — четыре, шесть и девять — [latex]6,3[/latex], округленное до десятых, поскольку данные представляют собой целые числа.
Большинство ответов будут округлены таким образом.
Уровни измерения
Способ измерения набора данных называется уровнем измерения . Правильные статистические процедуры зависят от того, знаком ли исследователь с уровнями измерения. Не каждую статистическую операцию можно использовать с каждым набором данных. Данные можно разделить на четыре уровня измерения. Это (от низшего к высшему уровню):
- Номинальный уровень шкалы
- Уровень порядковой шкалы
- Уровень шкалы интервалов
- Уровень шкалы отношений
Данные, измеренные с использованием номинальной шкалы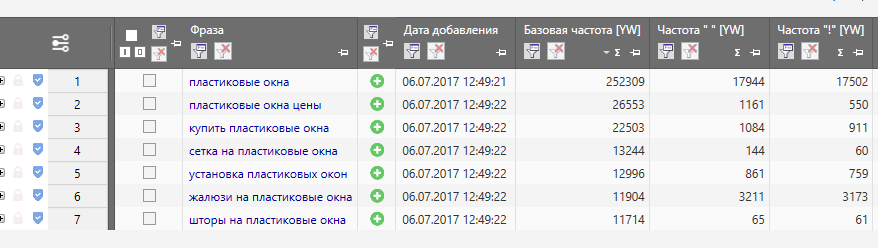 
Ставить пиццу на первое место, а суши — на второе, не имеет смысла.
Компании-смартфоны — еще один пример данных номинальной шкалы. Некоторыми примерами являются Sony, Motorola, Nokia, Samsung и Apple. Это всего лишь список, и нет согласованного порядка. Некоторые люди могут отдать предпочтение Apple, но это вопрос мнения. Данные номинального масштаба нельзя использовать в расчетах.
Данные, измеренные с использованием порядковой шкалы , аналогичны данным номинальной шкалы, но есть большая разница. Данные порядковой шкалы можно заказать. Примером данных в порядковой шкале является список пяти лучших национальных парков США. Пять лучших национальных парков США можно ранжировать от одного до пяти, но мы не можем измерить разницу между данными.
Другим примером использования порядковой шкалы является опрос о круизах, где ответы на вопросы о круизе: «отлично», «хорошо», «удовлетворительно» и «неудовлетворительно». Эти ответы упорядочены от наиболее желаемого ответа к наименее желательному.
Но различия между двумя фрагментами данных не могут быть измерены. Как и данные номинальной шкалы, данные порядковой шкалы нельзя использовать в расчетах.
Данные, измеренные с использованием интервальной шкалы , аналогичны данным порядкового уровня, поскольку они имеют определенный порядок, но между данными есть разница. Различия между данными шкалы интервалов могут быть измерены, хотя данные не имеют отправной точки.
Температурные шкалы, такие как шкалы Цельсия (C) и Фаренгейта (F), измеряются с помощью шкалы интервалов. В обоих измерениях температуры [латекс]40°[/латекс] равно [латекс]100°[/латекс] минус [латекс]60°[/латекс]. Различия имеют смысл. Но [латекс]0[/латекс] градусов не соответствует, потому что в обеих шкалах [латекс]0[/латекс] не является самой низкой температурой. Существуют такие температуры, как [латекс]-10°[/латекс] F и [латекс]-15°[/латекс] С, и они ниже, чем [латекс]0[/латекс].
Данные интервального уровня можно использовать в расчетах, но нельзя проводить один тип сравнения.
[латекс]80°[/латекс] C не в четыре раза горячее, чем [латекс]20°[/латекс] C (и [латекс]80°[/латекс] F в четыре раза горячее, чем [латекс]20° [/латекс] F). Нет смысла в соотношении [латекс]80[/латекс] к [латексу]20[/латекс] (или четыре к одному).
Данные, измеренные с использованием шкалы соотношений решают проблему соотношений и дают вам больше информации. Данные шкалы отношений аналогичны данным шкалы интервалов, но имеют точку [latex]0[/latex], и отношения можно рассчитать. Например, четыре финальных экзамена по статистике с несколькими вариантами ответов: [латекс]80[/латекс], [латекс]68[/латекс], [латекс]20[/латекс] и [латекс]92[/латекс] (из возможных [латексных]100[/латексных] баллов). Экзамены проходят машинную оценку.
Данные можно расположить в порядке от низшего к высшему: [латекс]20[/латекс], [латекс]68[/латекс], [латекс]80[/латекс], [латекс]92[/латекс].
Различия между данными имеют значение. Оценка [latex]92[/latex] больше, чем оценка [latex]68[/latex] на [latex]24[/latex] балла.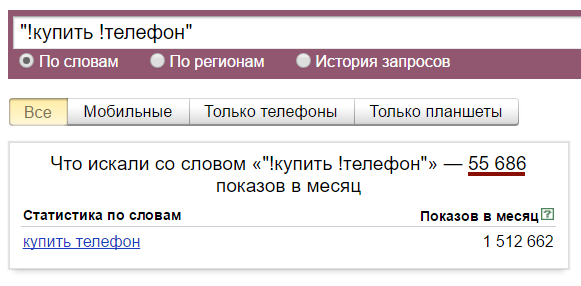
Коэффициенты можно рассчитать. Наименьшая оценка — [латекс]0[/латекс]. Итак, [латекс]80[/латекс] в четыре раза больше [латекс]20[/латекс]. Оценка [latex]80[/latex] в четыре раза лучше, чем оценка [latex]20[/latex].
Частота
Двадцать студентов спросили, сколько часов они работают в день. Их ответы в часах следующие: [латекс]5[/латекс], [латекс]6[/латекс], [латекс]3[/латекс], [латекс]3[/латекс], [латекс]2 [/латекс], [латекс]4[/латекс], [латекс]7[/латекс], [латекс]5[/латекс], [латекс]2[/латекс], [латекс]3[/латекс], [латекс]5[/латекс], [латекс]6[/латекс], [латекс]5[/латекс], [латекс]4[/латекс], [латекс]4[/латекс], [латекс]3[ /латекс], [латекс]5[/латекс], [латекс]2[/латекс], [латекс]5[/латекс], [латекс]3[/латекс].
В следующей таблице перечислены различные значения данных в порядке возрастания и их частоты.
| ЗНАЧЕНИЕ ДАННЫХ | ЧАСТОТА |
|---|---|
| [латекс]2[/латекс] | [латекс]3[/латекс] |
| [латекс]3[/латекс] | [латекс]5[/латекс] |
| [латекс]4[/латекс] | [латекс]3[/латекс] |
| [латекс]5[/латекс] | [латекс]6[/латекс] |
| [латекс]6[/латекс] | [латекс]2[/латекс] |
| [латекс]7[/латекс] | [латекс]1[/латекс] |
Частота — это количество раз, когда значение данных встречается. Согласно таблице, трое студентов работают два часа, пять студентов работают три часа и так далее. Сумма значений в столбце частот [latex]20[/latex] представляет собой общее количество учащихся, включенных в выборку.
Относительная частота — это отношение (доля или пропорция) количества раз, когда значение данных встречается в наборе всех результатов, к общему количеству результатов. Чтобы найти относительные частоты, разделите каждую частоту на общее количество студентов в выборке — в данном случае [латекс]20[/латекс]. Относительные частоты могут быть записаны в виде дробей, процентов или десятичных знаков.
| ЗНАЧЕНИЕ ДАННЫХ | ЧАСТОТА | ОТНОСИТЕЛЬНАЯ ЧАСТОТА |
|---|---|---|
| [латекс]2[/латекс] | [латекс]3[/латекс] | [латекс]\displaystyle\frac{3}{20}[/латекс] или [латекс]0,15[/латекс] |
| [латекс]3[/латекс] | [латекс]5[/латекс] | [латекс]\displaystyle\frac{5}{20}[/латекс] или [латекс]0,25[/латекс] |
| [латекс]4[/латекс] | [латекс]3[/латекс] | [латекс]\displaystyle\frac{3}{20}[/латекс] или [латекс]0,15[/латекс] |
| [латекс]5[/латекс] | [латекс]6[/латекс] | [латекс]\displaystyle\frac{6}{20}[/латекс] или [латекс]0,30[/латекс] |
| [латекс]6[/латекс] | [латекс]2[/латекс] | [латекс]\displaystyle\frac{2}{20}[/латекс] или [латекс]0,10[/латекс] |
| [латекс]7[/латекс] | [латекс]1[/латекс] | [латекс]\displaystyle\frac{1}{20}[/латекс] или [латекс]0,05[/латекс] |
Сумма значений в столбце относительной частоты предыдущей таблицы равна [латекс]\фракция{20}{20}[/латекс] или [латекс]1[/латекс].
Суммарная относительная частота — это накопление предыдущих относительных частот. Чтобы найти совокупные относительные частоты, добавьте все предыдущие относительные частоты к относительной частоте для текущей строки, как показано в таблице ниже.
| ЗНАЧЕНИЕ ДАННЫХ | ЧАСТОТА | РОДСТВЕННИК ЧАСТОТА | СОВОКУПНЫЙ ОТНОСИТЕЛЬНЫЙ ЧАСТОТА |
|---|---|---|---|
| [латекс]2[/латекс] | [латекс]3[/латекс] | [латекс]\displaystyle\frac{3}{20}[/латекс] или [латекс]0,15[/латекс] | [латекс]0,15[/латекс] |
| [латекс]3[/латекс] | [латекс]5[/латекс] | [латекс]\displaystyle\frac{5}{20}[/латекс] или [латекс]0,25[/латекс] | [латекс] 0,15 + 0,25 = 0,40 [/латекс] |
| [латекс]4[/латекс] | [латекс]3[/латекс] | [латекс]\displaystyle\frac{3}{20}[/латекс] или [латекс]0,15[/латекс] | [латекс] 0,40 + 0,15 = 0,55 [/латекс] |
| [латекс]5[/латекс] | [латекс]6[/латекс] | [латекс]\displaystyle\frac{6}{20}[/латекс] или [латекс]0,30[/латекс] | [латекс] 0,55 + 0,30 = 0,85 [/латекс] |
| [латекс]6[/латекс] | [латекс]2[/латекс] | [латекс]\displaystyle\frac{2}{20}[/латекс] или [латекс]0,10[/латекс] | [латекс] 0,85 + 0,10 = 0,95 [/латекс] |
| [латекс]7[/латекс] | [латекс]1[/латекс] | [латекс]\displaystyle\frac{1}{20}[/латекс] или [латекс]0,05[/латекс] | [латекс] 0,95 + 0,05 = 1,00 [/латекс] |
Последняя запись в столбце кумулятивной относительной частоты равна единице, что указывает на то, что накоплено сто процентов данных.
ПРИМЕЧАНИЕ
Из-за округления сумма столбца относительной частоты может не всегда равняться единице, и последняя запись в столбце совокупной относительной частоты может не быть единицей. Однако каждый из них должен быть близок к единице.
Обзор концепции
Некоторые расчеты генерируют искусственно точные числа. Нет необходимости сообщать значение с точностью до восьми знаков после запятой, если измерения, сгенерировавшие это значение, были точными только до ближайшей десятой. Округлите окончательный ответ на один знак после запятой больше, чем было в исходных данных. Это означает, что если у вас есть данные, измеренные с точностью до десятых долей, сообщайте окончательную статистику с точностью до сотых.
Помимо округления ответов, вы можете измерить свои данные, используя следующие четыре уровня измерения.
- Номинальный уровень шкалы: данные, которые нельзя ни заказать, ни использовать в расчетах
- Порядковый уровень шкалы: данные, которые можно заказать; различия не могут быть измерены
- Уровень интервальной шкалы: данных с определенным порядком, но без начальной точки; различия можно измерить, но такого понятия, как отношение, не существует.
- Уровень шкалы отношений: данных с начальной точкой, которую можно заказать; различия имеют смысл, и отношения могут быть рассчитаны.
При организации данных важно знать, сколько раз встречается значение. Сколько студентов, изучающих статистику, готовятся к экзамену пять или более часов? Какой процент семей в нашем квартале имеет двух домашних животных? Частота, относительная частота и кумулятивная относительная частота — это меры, которые отвечают на подобные вопросы.
Каталожные номера
«Краткие сведения о штатах и округах», Бюро переписи населения США. http://quickfacts.census.gov/qfd/download_data.html (по состоянию на 1 мая 2013 г.).
«Краткие сведения о штатах и округах: быстрый и простой доступ к фактам о людях, бизнесе и географии», Бюро переписи населения США. http://quickfacts.census.gov/qfd/index.html (по состоянию на 1 мая 2013 г.).
«Таблица 5: Прямые попадания ураганов на материковой части США (1851–2004 гг.
)», Национальный центр ураганов, http://www.nhc.noaa.gov/gifs/table5.gif (по состоянию на 1 мая 2013 г.).
«Уровни измерения», http://infinity.cos.edu/faculty/woodbury/stats/tutorial/Data_Levels.htm (по состоянию на 1 мая 2013 г.).
Кортни Тейлор, «Уровни измерения», about.com, http://statistics.about.com/od/HelpandTutorials/a/Levels-Of-Measurement.htm (по состоянию на 1 мая 2013 г.).
Дэвид Лейн. «Уровни измерения», Connexions, http://cnx.org/content/m10809/latest/ (по состоянию на 1 мая 2013 г.).
load — как рассчитать частоту вызова метода
спросил
Изменено 5 лет, 4 месяца назад
Просмотрено 319 раз
Я хочу написать простой балансировщик нагрузки.
Допустим, у меня есть два сервера, на которых запущен один и тот же веб-сервис.
Балансировщику нагрузки необходимо знать, сколько раз веб-служба недавно вызывалась на каждом сервере. Нижний вызываемый сервер будет рекомендован для использования клиентом.
Веб-служба может быть вызвана многими клиентами одновременно.
Мне нужен способ подсчитать, сколько раз метод вызывался в последнюю минуту. Лучше не использовать блокировку для блокировки параллельного вызова и не использовать слишком много памяти. Время вызова метода не обязательно должно быть точным.
- load
- rate
Итак, как насчет однопоточного асинхронного ввода-вывода (т. е. node.js или Twisted/Tornado?), балансировщик нагрузки будет маршрутизировать запросы, пока он поддерживает необходимые подсчеты (блокировки не требуются)? Как обновление одного счетчика, так и передача запроса должны быть быстрыми, «неблокирующими» операциями.
Обе библиотеки в основном представляют собой инструменты мультиплексирования ввода-вывода, которые полностью используют один единственный поток, а не создают несколько потоков.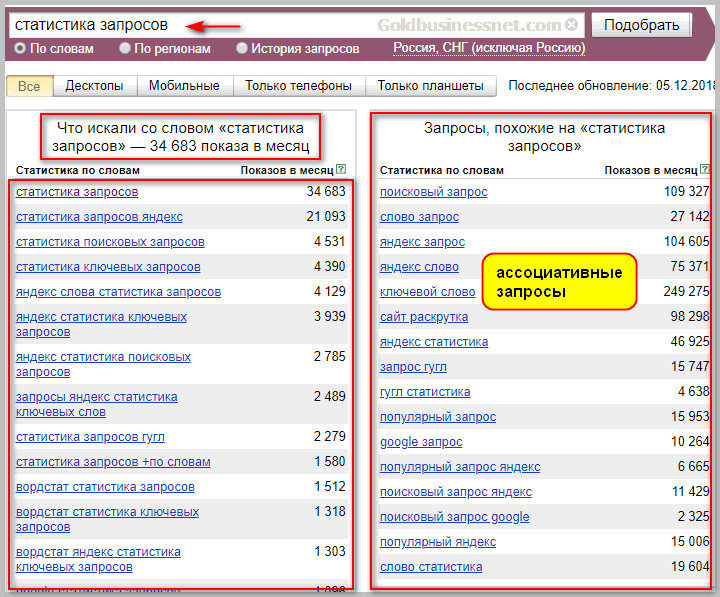
Учитывая, что большая часть времени выполнения сетевых приложений находится в ожидании ввода-вывода, способность одного потока выполнять другой код во время ввода-вывода делает его способным соответствовать или превосходить производительность многопоточных серверов. Для этого он использует функции epoll/select, подобные функциям ОС. Одним из преимуществ является то, что синхронизация не требуется.
Несколько довольно минимальных рабочих примеров для прокси в tornado (python) и node.js: https://codeforgeek.com/2015/12/обратный-прокси-использование-expressjs/ https://gist.github.com/netdesign/1267537/635425784393fc8397fb928d1e573e4495696d82
Чтобы использовать скользящую сумму, вам необходимо определить окно (оценочное количество вызовов за период, указанный в окне).
Затем (псевдокод):
var server1sum = 0, сервер2сумма = 0, маршруты = [], window = <количество сохраняемых запросов>; маршрут функции (запрос): если сумма_сервера < сумма_сервера: маршрут_запрос (сервер1) маршруты.
