Уникальность текста: что это такое
Уникальность текста – это показатель, который определяет, нет ли в текстовом контенте заимствований из других текстов. Уникальность – один из базовых показателей качества: если контент неуникальный и дублируется на других сайтах, на ресурс, который разместил дубль, скорее всего, наложит санкции поисковик. Параметр влияет и на отношение пользователя: к площадкам, которые размещают заимствованный чужой контент, доверия меньше. Вдобавок люди заслуженно считают такие ресурсы менее полезными.
Классификация уникальностиПо типу. Поскольку «уникальность» – понятие размытое, выделяют несколько ее видов:
- формальная
– определяет, не содержит ли текст заимствований словесных блоков.
Оцениваются только технические параметры: использование конкретных фраз,
структура, объем, порядок слов. Такое определение уникальности никак не
затрагивает смысловое наполнение. Полностью уникальный формально текст
может дублировать по смыслу другие аналогичные записи в интернете.

- смысловая уникальность полностью противоположна формальной. Оценивается не столько оригинальность структуры, сколько новизна идей, изложенных в тексте. Уникальный по смыслу текст содержит идеи, которые не публиковались больше нигде. Высокую смысловую уникальность имеют экспертные статьи, информационные сводки: их обычно пишут профессионалы в своей нише – делятся сведениями, которых ни у кого нет.
Оптимальный контент – тот, который уникален и по смыслу, и формально.
По источнику. Еще одна классификация разделяет уникальность не по подаче информации и содержанию, а относительно источника:
- внутренняя – определяет, насколько текст уникален внутри сайта;
- внешняя – дает представление, нет ли заимствований на других ресурсах.
Значение
имеют оба типа. Чтобы продвинуть сайт и избежать санкций, следует
добиваться того, чтобы каждый текст был уникален и в пределах источника,
и относительно других сайтов.
Показатель не бинарная переменная, имеющая только два значения «да» и «нет». Чаще всего оригинальность текста выражают в процентном соотношении.
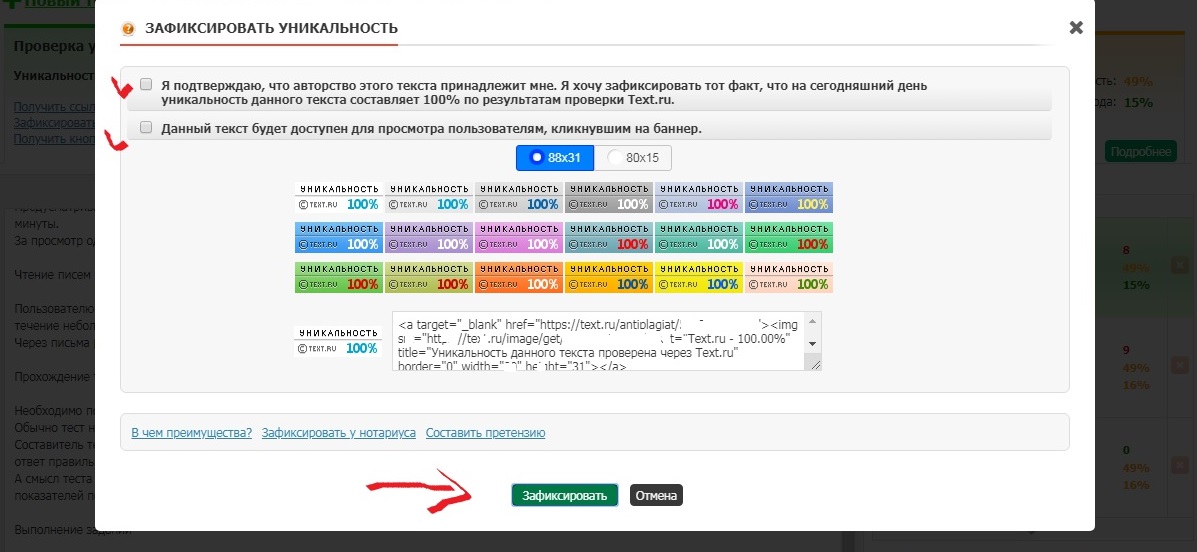
- Полностью скопированные тексты имеют оригинальность ниже 10 %. Чаще всего 0 %, если контент позаимствован полностью. Это очень плохо, причем и для сайта, скопировавшего информацию, и для изначального источника: если поисковик не разберется, кто именно позаимствовал текст, под санкции могут попасть оба сайта. К счастью, вебмастерские панели позволяют заявить об авторстве.
- Меньше 50 % получают тексты, которые срерайтили с других (то есть переписали своими словами), причем не очень качественно, с сохранением структуры и отдельных фраз. Такой контент не рекомендуется публиковать: можно ухудшить позиции.
- До 80 % набирает качественный рерайт. Такие тексты не вредят позициям, их можно размещать.
- Значение выше 80 % говорит, что текст уникален и сможет «работать» для продвижения.

Идеальный показатель – 100 %, но он не всегда достижим. Например, если статья техническая или юридическая и содержит много длинных тяжеловесных терминов, это бьет по проценту оригинальности. Повышать уникальность по возможности рекомендуется, но не в ущерб смыслу и содержанию.
Структура. При оценке уникальности специальные сервисы смотрят на сходство последовательностей слов. Уменьшить это сходство можно, изменив структуру, поменяв местами блоки или абзацы. Это касается и пунктов списка, и даже простых словосочетаний: замена «деревянного дома» на «дом из дерева» повысит оригинальность.
Клише и канцеляризмы.
Люди во время разговора используют штампы, устоявшиеся выражения. Это
характерно и для письменной речи: в каждой тематике есть свои клише. При
написании статьи такие штампы способны серьезно повредить уникальности,
хотя особенной смысловой нагрузки они не несут и пользы тексту не
приносят. От них следует избавляться.
Заголовки. Уникальность может снизиться из-за подзаголовка, состоящего из шаблонной фразы («что делать», «как это работает» и т. д.), или из-за блока текста, не разбитого заголовками на части. Следите за подзаголовками: если это нужно, вставляйте новые или перефразируйте существующие.
Абзацы и списки. Маркированные списки можно представить в виде текста, разбитого на абзацы, и наоборот: информацию, поданную одним блоком текста, переписать как набор пунктов. Если поменять порядок предложений, уникальность повысится дополнительно.
Добавление слов. Не бойтесь играть
со словесными конструкциями. Даже при рерайте можно подать ту же самую
информацию по-новому и сделать текст полностью уникальным. Добавляйте
новые слова, заменяйте фразы на синонимы, а если найдете где-то другие
актуальные сведения, можете написать о них своими словами – текст от
этого только выиграет. Главное – следить, чтобы информация была
достоверной, иначе пострадает смысл.
Добавляйте
новые слова, заменяйте фразы на синонимы, а если найдете где-то другие
актуальные сведения, можете написать о них своими словами – текст от
этого только выиграет. Главное – следить, чтобы информация была
достоверной, иначе пострадает смысл.
Смысловую оригинальность сможет проверить только человек, а вот для определения процента формальной уникальности существует несколько популярных сервисов. Работают они все по похожему принципу: исключают служебные слова (предлоги, междометия и т. д.), разбивают текст на шиндлы (короткие последовательности из нескольких слов) и ищут аналогичные словесные блоки по всему интернету. Чем меньше размер шиндла, тем более строгой окажется проверка. В некоторых сервисах это можно настраивать. Неуникальные фрагменты программа обычно подсвечивает, чтобы их было удобнее найти.
Онлайн-сервисы. Позволяют проверять текст
прямо на странице сайта. Обычно это дочерние сервисы бирж копирайтинга
или ресурсов по продвижению, некоторые крупные организации используют
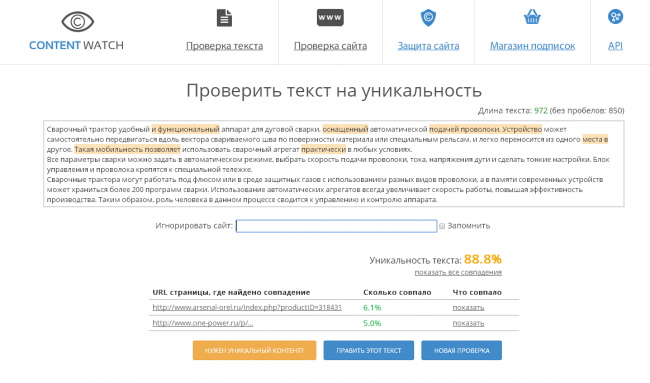
самописные системы.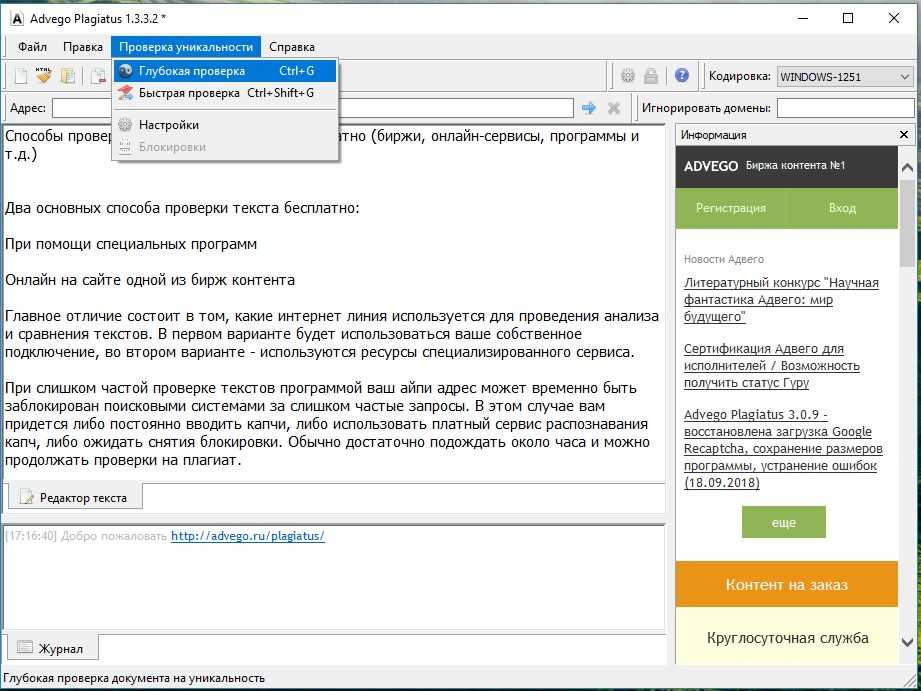 Из ярких примеров – Text.Ru, Miratools. Популярные
ресурсы имеют ограничения на объем текста и реагируют на запросы
пользователей в порядке очереди из-за высокой нагрузки.
Из ярких примеров – Text.Ru, Miratools. Популярные
ресурсы имеют ограничения на объем текста и реагируют на запросы
пользователей в порядке очереди из-за высокой нагрузки.
Офлайн-приложения. Программы для определения уникальности можно установить на компьютер. Обычно они имеют более широкую функциональность, но в свою очередь требуют внимания со стороны пользователя, например ввода капчи. Пример – «ETXT Антиплагиат».
что это такое, как ее проверить, повысить и что это значит для продвижения
Делаем вашу страницу интересной и стимулируем подписчиков почаще заглядывать к вам на страницу или на сайт за покупками
Свежие публикации регулярно
Получи нашу книгу «Контент-маркетинг в социальных сетях: Как засесть в голову подписчиков и влюбить их в свой бренд».
Подпишись на рассылку и получи книгу в подарок!
Уникальность текста — это параметр качества материала, он показывает, какой процент текста заимствован из других источников без изменения.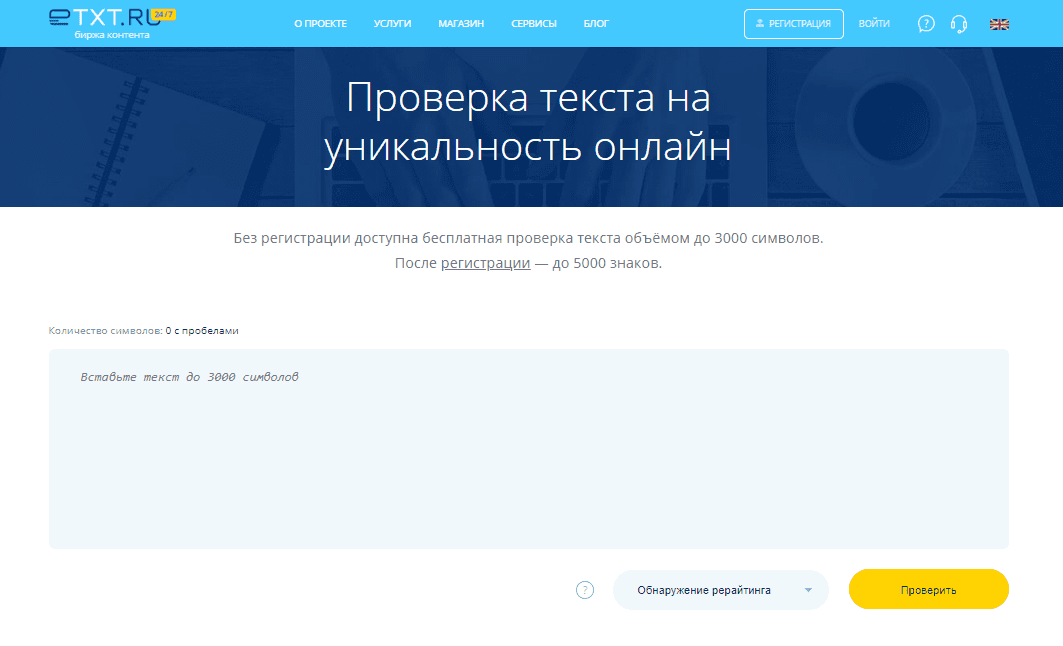
Больше видео на нашем канале — изучайте интернет-маркетинг с SEMANTICA
- Важность уникальности
- Синонимайзеры
- Проверка текста на уникальность онлайн
- Advego Plagiatus
- Текст.ру
- Как повысить уникальность
Уникальным считается тот текст, который больше нигде не встречается.
Например, на сайте А есть текст: “Съешь же еще этих французских булок. И выпей чай.” На сайте Б — текст: “Съешь же еще этих французских булок. Запей кофе. И ложись спать.” В статье сайта Б будет считаться заимствованным первое предложение. Ведь оно уже встречалось на сайте А.
Можно рассчитать процент уникальности материала. Это будет отношение объемов заимствованного текста и авторского.
Это будет отношение объемов заимствованного текста и авторского.
Таким образом, при наличии нулевой уникальности можно смело говорить о полном и безоговорочном плагиате, а при обратном варианте (100%) об оригинальности изложенного материала и отсутствию найденных совпадений с иными статьями. Для тех, кто желает расставить все по полочкам существует даже специальная общепринятая шкала:
- 95-100% — чрезвычайно высокий уровень уникальности.
- 90-95% — высокий уровень.
- 80-90% — средняя уникальность (вызывает вопросы).
- 79% и ниже – низкий уровень уникальности.
Существует множество инструментов, которые помогут определить уникальность написанного материала, причем работают они по различным принципам и выдают действительно реальный результат. Как именно и чем проверить текст на уникальность мы расскажем чуть ниже.
Важность уникальности
Введем два важных определения.
- Копирайтинг — написание уникального материала с нуля.

- Рерайтинг — за основу берется готовый текст, но полностью переписывается.
Когда-то для того, чтобы материал считался уникальным, достаточно было поменять местами слова в предложении, немного поменять падежи.
Сейчас поисковые системы заинтересованы в том, чтобы давать пользователю уникальный, авторский материал. И анализируется не просто порядок слов, но даже схожесть синонимов, структуры.
Потому текст должен быть оригинальным и осмысленным, для того, чтобы веб-сайт всегда находился на вершине выдачи. Все поисковики, к примеру, Google, Mail.ru, «Рамблер», Yahoo,
Уникальные тексты ценятся всеми поисковиками. Поэтому каждая статья на вашем сайте должна быть уникальной, неповторимой. И полезной для читателя, то есть, давать ему тот материал, который он больше нигде не увидит.
Синонимайзеры
Уникальность теста чрезвычайно важна, при этом, рерайт позволяет добиться исключительно технической оригинальности, оставляя смысловую нагрузку взятых для работы источников.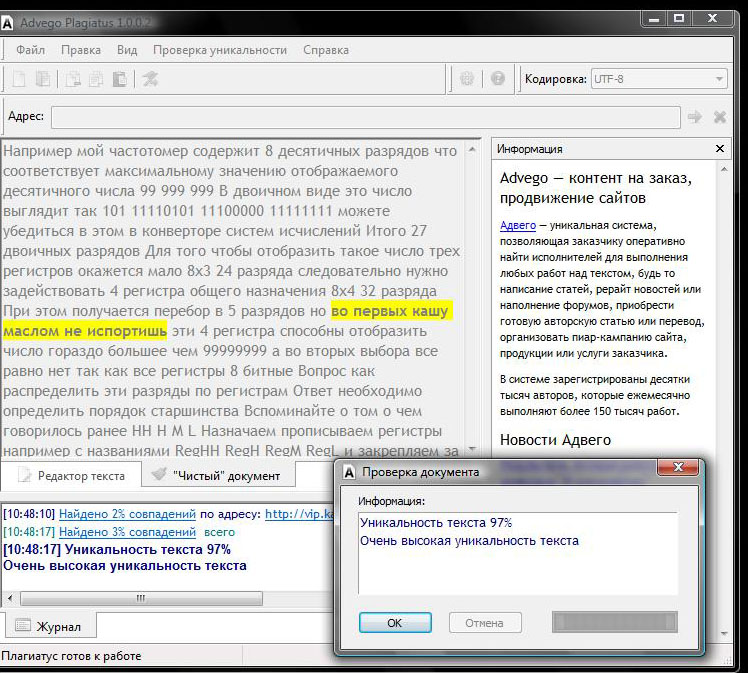
Они помогают подобрать синонимы ко всем или некоторым словам, порой удивляя своей эффективностью. Однако в большинстве случаев после обработки таким софтом тексты требуют весьма серьезной доработки и исправлений.
- Supernatural synonymizer – удобная программа, помогающая сделать текст уникальнее, без танцев с бубном, отправки платных СМС и даже регистрации на портале.
- USyn – еще один чрезвычайно выгодный вариант, помогающий каждому отыскать множество вариантов написания одного и того же по смыслу предложения. Тут можно отсеять стоп-слова и выбрать наиболее подходящий синоним.
- Бесплатный online синонимайзер русского текста http://fromtlt.ru/sinonim/# предлагает быстрый подбор синонимов. Однако качество выдаваемого текста, конечно же, тоже оставляет желать лучшего.

Все эти сервисы работают по принципу простой замены неуникального слова синонимом. Машина не всегда подбирает лучший и правильный вариант. Так что дорабатывать материал все равно придется.
Проверка текста на уникальность онлайн
Есть разные, платные и бесплатные сервисы проверки текстов.
Advego Plagiatus
https://advego.ru/plagiatus/
Наиболее известным софтом, что сперва требуется установить на свое устройство, является пресловутый Advego Plagiatus, о котором слушал и использовал хотя бы несколько раз каждый копирайтер в сети. Причем этот сервис имеет множество дополнительных функций и удобных проверок, благодаря интеллектуальным алгоритмам проверок.
- Синонимайзинг и перестановку местами слов не помогут обойти проверку, так как происходит лексический анализ текстов.
- Замена букв в словах символами из другой раскладки тоже уже не пройдет, антиплагиат отыщет и выделяет подобные места.
- Текст на проверке автоматически очищается от невидимых или любых иных (к примеру, разметочных) символов, которые были установлены для повышения уникальности.

- Отсеивается также изменение падежей, времени, вставка «водных» слов и целых фраз.
Чтобы сделать материал действительно уникальным, лучше использовать не один и два, а пять-семь источников, из которых и выводить наиболее важные мысли и фразы. Избавляйтесь от воды и общепринятых штампов, тогда хорошие результаты вам гарантированы.
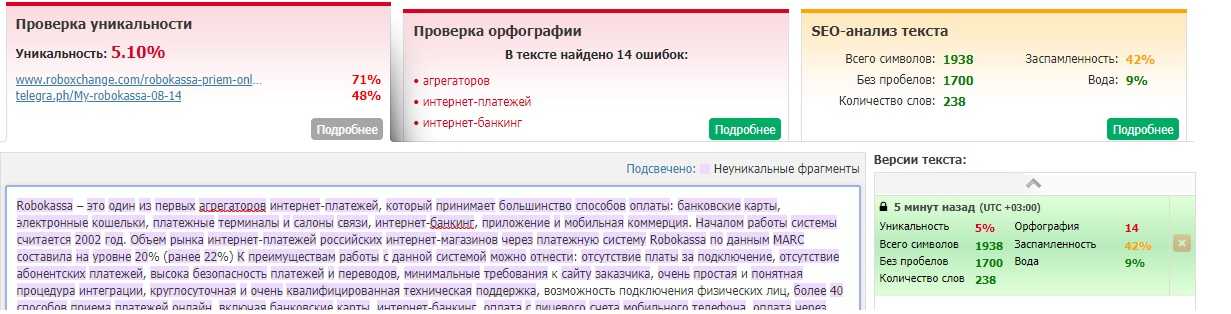
Текст.ру
https://text.ru/antiplagiat
Это еще один популярный сервис
- Программа легко обнаруживает вариант с заменой каждого четвертого слова в материале, что было действенно ранее.
- Интеллектуальный алгоритм проверки позволяет выявить переставленные местами слова, проводя общий анализ материала.
- Добавление «лишних» слов, к примеру, дополнительных определений, тоже не поможет обмануть умную программу, такие участки будут выявлены быстро и просто.
Добиться большого процента уникальности по версии Text.ru. не так и сложно. Главное тут применять несколько источников, пользоваться собственным воображением и словарным запасом, а также писать тексты самостоятельно. Постарайтесь перефразировать, изменить фразы, что подсвечиваются фиолетовым и вы увидите, как все быстро меняется в лучшую сторону в процентном соотношении.
Постарайтесь перефразировать, изменить фразы, что подсвечиваются фиолетовым и вы увидите, как все быстро меняется в лучшую сторону в процентном соотношении.
Как повысить уникальность
Проверив текст и увидев, что уникальность его недостаточно высока, придется браться за работу и для этого вовсе не обязательно использовать какой-либо софт (программы-синонимайзеры). Чтобы проверка, а вслед затем и поисковые роботы приняли вашу работу, как уникальную, можно последовать нескольким простым советам, которые нетрудно запомнить.
- Начните изменения с самого заголовка, так как зачастую все дело кроется именно в нем. Н1 должен быть емким, четким, можно использовать в нем ключевые запросы, но перебарщивать не стоит.
- Перепишите начало, так как именно оттуда и начинаются все остальные проблемы. Поисковые машины в первую очередь проверяют именно начало и «видят», откуда оно могло бы быть скопировано.
- В середине текста достаточно будет изменить падежи, время, заменить слова синонимами, более читаемыми и емкими.
 Так времени можно будет истратить меньше, а результат получить гораздо выше.
Так времени можно будет истратить меньше, а результат получить гораздо выше. - Завершающая часть текста не менее важна, чем его начало, потому и над ней стоит поработать, а при потребности и переписать полностью, от первого и до последнего слова.
- Нужно учитывать, что чаще всего на вершине выдачи появляется тот материал, который полностью правильно отформатирован, потому стоит уделить данному моменту достаточно внимания.
- При добавлении ссылок на другие статьи и веб-сайты уникальность текста только выигрывает.
Последним советом, который хотелось бы озвучить, остается тот, что всегда следует оставаться собой и писать тексты исключительно от себя, как говорят, по зову сердца, тогда и получится оригинально. Используйте вступления, заключения, списки, ссылки и все, что только может прийти вам в голову, главное добиться нужной читабельности и уникальности, а при определенном уровне понимания таких процессов это вполне выполнимо.
5 причин, по которым ваша оценка эссе зависит от уникальности текста
Большинство старшеклассников и студентов знакомы с термином плагиат. Это акт кражи чьей-либо интеллектуальной собственности путем ее копирования в вашем академическом эссе или статье. Некоторые учащиеся делают это без особого намерения, поэтому они могут выполнить задания высокого качества, но забывают отдать должное первоначальным авторам, работая над различными типами эссе.
Это акт кражи чьей-либо интеллектуальной собственности путем ее копирования в вашем академическом эссе или статье. Некоторые учащиеся делают это без особого намерения, поэтому они могут выполнить задания высокого качества, но забывают отдать должное первоначальным авторам, работая над различными типами эссе.
Как только у вас появятся интересные идеи для эссе, вы сразу же начнете искать подходящие источники, которые вы можете использовать для поиска информации и данных. Тем не менее, вы должны научиться проверять плагиат, чтобы убедиться, что он уникален. Вот почему оценка вашего эссе зависит от проверки на плагиат и уникальности вашего текста.
ИЗОБРАЖЕНИЕ: PEXELS
1. Учителя и профессора должны оценить вашу работу
Основная цель задания эссе — проверить понимание учащимися и выяснить, кто действительно усердно работал над изучением темы. Профессора имеют доступ к надежным инструментам, которые позволяют им обнаруживать скопированный текст, поэтому они узнают, не является ли ваше эссе на 100% уникальным и оригинальным.
Некоторые учащиеся присылают плагиатные тексты, не желая этого. Они либо забывают соблюдать правильные правила цитирования, либо у них нет доступа к профессиональной проверке на плагиат. Эти онлайн-инструменты помогают учащимся и учителям обнаруживать скопированный текст и предпринимать необходимые действия. Средство проверки на плагиат помогает иностранным студентам, которые дома не привыкли к проблемам уникальности.
Если вы не можете написать или отправить эссе своими словами, учителя и преподаватели не поставят вам справедливую оценку, потому что они не могут оценить ваш фактический уровень понимания. Вам действительно может понадобиться помощь профессора, а они не окажут вам должной помощи, потому что вы копируете чужую работу.
2. Учащиеся должны проявить свою индивидуальность
Когда учащиеся пишут эссе, это их шанс выразить себя и свое мнение. Если вы копируете другой источник или занимаетесь плагиатом, вы не покажете свою индивидуальность. Написание академического эссе позволяет учащимся проявить творческий подход в безопасной среде.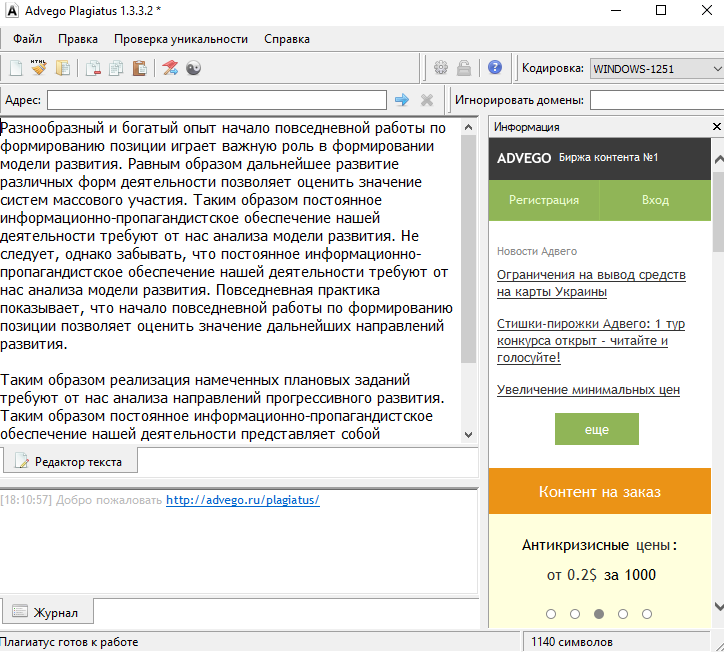
Они могут обсуждать любую тему или даже выбирать особую тему, о которой они могут писать. Они могут рассказывать свои собственные истории и даже использовать эти тексты для передачи определенных сообщений. Академическое эссе может продвигать определенное благое дело или убеждать людей в необходимости действовать. Вы не должны упускать этот шанс, копируя чужую работу.
3. Опирайтесь на предыдущую литературу
Тот факт, что вы используете ранее опубликованный источник, не означает, что он на 100% верен. С развитием технологий сегодняшние студенты имеют доступ к множеству различных источников и инструментов, которые позволяют им сравнивать записи и выделять противоречивые данные. Ваше эссе может быть вашим шансом указать на ошибки в другом ресурсе или на несоответствие между несколькими онлайн-источниками и книгами.
Студенты должны признавать интеллектуальную собственность, избегать плагиата и отдавать должное оригинальному автору любого заимствованного текста.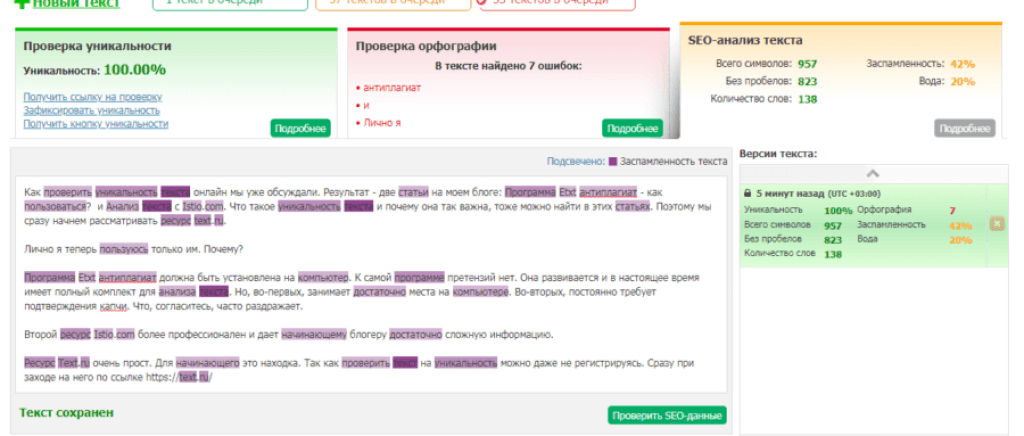 В конце концов, научный прогресс никогда не был бы возможен, если бы ученые и студенты не могли изучать ранее опубликованную литературу. Вы можете делиться работой других людей, но вы также должны признавать их усилия.
В конце концов, научный прогресс никогда не был бы возможен, если бы ученые и студенты не могли изучать ранее опубликованную литературу. Вы можете делиться работой других людей, но вы также должны признавать их усилия.
Когда вы пишете свои собственные слова, вы можете создать новое и уникальное значение, выражающее ваше мнение по определенной теме. После того, как вы процитируете работу других, очень важно добавить свои собственные слова и объяснить их ценность.
4. Улучшите свои навыки письма
Работа над академическими эссе поможет вам улучшить свои навыки письма. Это один из самых важных навыков, который вы можете использовать позже, когда будете работать. Письменное общение — один из самых важных инструментов, который люди используют независимо от выбора своей карьеры. Независимо от того, что вы решите изучать, позже вам, вероятно, придется представить письменный отчет или статью, которая должна быть выполнена в отличном качестве.
Учащиеся, которые не умеют хорошо писать, становятся лучшими авторами, если пишут часто. Академические эссе дают людям возможность указать на свои ошибки и исправить их, чтобы они стали лучшими писателями. Когда они заканчивают учебу, они могут лучше писать электронные письма и деловые предложения, потому что у них была возможность учиться и получать рекомендации от своих учителей и профессоров.
Академические эссе дают людям возможность указать на свои ошибки и исправить их, чтобы они стали лучшими писателями. Когда они заканчивают учебу, они могут лучше писать электронные письма и деловые предложения, потому что у них была возможность учиться и получать рекомендации от своих учителей и профессоров.
Если учащиеся мало практикуются и отправляют неуникальный текст, они могут получить незаслуженную оценку, но не узнают ничего, что могло бы им пригодиться в дальнейшем. Плагиат не поможет вам улучшить свои навыки письма.
5. Избегайте обвинений в плагиате
Основная причина, по которой учителя выявляют плагиат и проверяют уникальность для оценки вашего эссе, заключается в том, что последствия плагиата негативно сказываются на вашем академическом и профессиональном будущем. Плагиатные эссе и статьи обычно отклоняются, а студенты, которые их представляют, обычно наказываются. Студенты, которые рискуют, предлагая неуникальный текст, обычно повторяют свою работу. Это настоящая проблема, особенно если у них приближается крайний срок.
Это настоящая проблема, особенно если у них приближается крайний срок.
Если вы не хотите тратить свое время и силы, то вам следует проверить свой текст на уникальность с помощью программы проверки на плагиат до установленного срока. Это позволит преподавателям проверить вашу работу, объективно оценить ее и поставить вам оценку, которую вы действительно заслуживаете.
Учителя ценят вашу работу, а письму всегда нужно учиться. Вам не нужно беспокоиться о том, чтобы каждый раз отправлять идеальные эссе. Оригинальные эссе всегда будут впечатлять окружающих, даже если они содержат несколько ошибок. Это ваш шанс узнать, как стать лучше.
Если вас интересуют еще больше статей и информации, связанных с образом жизни, от нас здесь, в Bit Rebels, у нас есть из чего выбрать.
ИЗОБРАЖЕНИЕ: PEXELS
Энтропия | Бесплатный полнотекстовый | Относительная энтропия, гауссова концентрация и единственность равновесных состояний
1.
 Введение
Введение1.1. Критерии уникальности для мер Гиббса
В математической статистической механике важно иметь хорошие и полезные критерии отсутствия фазового перехода или, что то же самое, уникальности меры Гиббса, связанной с данным потенциалом. Такие критерии, также известные под названием высокотемпературных критериев, показывают, что при достаточно малом взаимодействии (высокая температура) фазовый переход отсутствует, а уникальная фаза обладает сильными перемешивающими свойствами, т. е. близка к степени произведения (бесконечная температура).
Наиболее известным среди таких критериев является критерий единственности Добрушина; см., например, ([1], гл. 8). По критерию единственности Добрушина, помимо единственности, выводятся сильные перемешивающие свойства единственной меры Гиббса, т. е. количественные оценки убывания ковариации локальных наблюдаемых, и количественные оценки разности между ожиданиями конечного и бесконечного объема, т. е. влияние граничного условия на математическое ожидание локальной функции. Основная идея критерия единственности Добрушина состоит в том, что, когда он выполняется, оператор условного ожидания действует как сжатие на пространстве вероятностных мер, снабженном расстоянием Вассерштейна. Поскольку мера Гиббса является неподвижной точкой этого сжатия, а неподвижные точки сокращений единственны, получается единственность мер Гиббса. Позднее критерий Добрушина был обобщен до критерия Добрушина–Шлосмана, и была установлена связь между этим критерием и важным функциональным неравенством — логарифмическим неравенством Соболева. Точнее, для глауберовской динамики спинов Изинга с конечным радиусом в [2] доказана эквивалентность критерия Добрушина-Шлосмана лог-неравенству Соболева. Это означает, например, что по критерию Добрушина–Шлосмана обратимая динамика Глаубера экспоненциально быстро (в L∞) сходится к своей единственной стационарной мере.
Основная идея критерия единственности Добрушина состоит в том, что, когда он выполняется, оператор условного ожидания действует как сжатие на пространстве вероятностных мер, снабженном расстоянием Вассерштейна. Поскольку мера Гиббса является неподвижной точкой этого сжатия, а неподвижные точки сокращений единственны, получается единственность мер Гиббса. Позднее критерий Добрушина был обобщен до критерия Добрушина–Шлосмана, и была установлена связь между этим критерием и важным функциональным неравенством — логарифмическим неравенством Соболева. Точнее, для глауберовской динамики спинов Изинга с конечным радиусом в [2] доказана эквивалентность критерия Добрушина-Шлосмана лог-неравенству Соболева. Это означает, например, что по критерию Добрушина–Шлосмана обратимая динамика Глаубера экспоненциально быстро (в L∞) сходится к своей единственной стационарной мере.
Связанный с критерием Добрушина, существует общий критерий в контексте взаимодействующих систем частиц, при котором достигается единственность стационарной меры и равномерная эргодичность, т.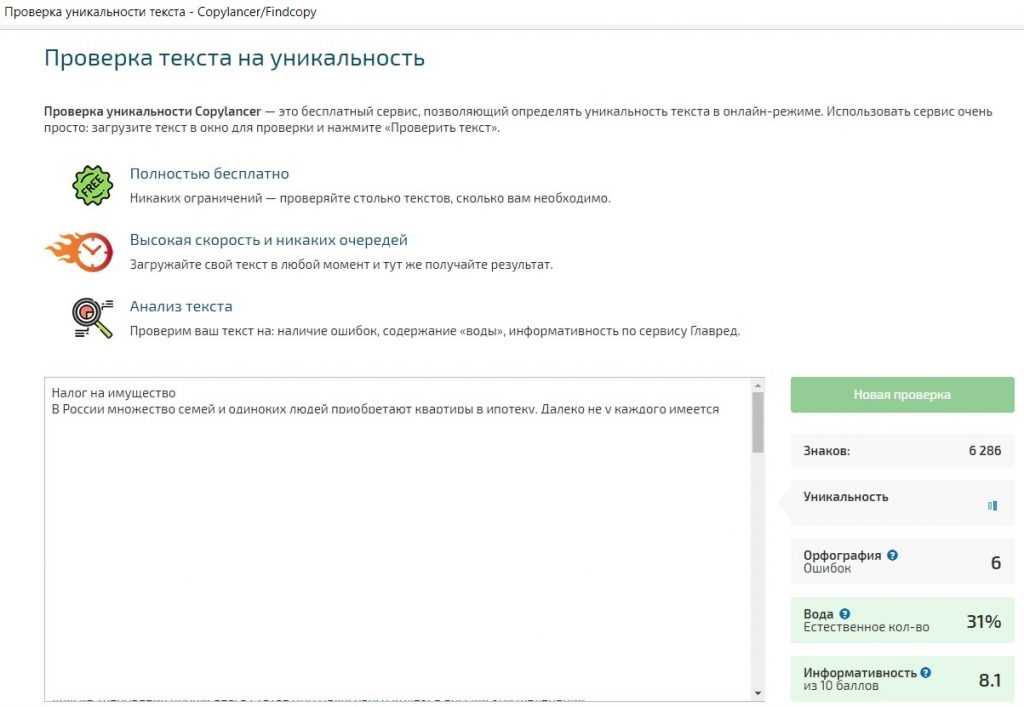 е. от любых начальных мер динамика во времени экспоненциально быстро сходится к уникальные стационарные меры. Этот критерий, так называемый «критерий M<ε» ([3], гл. 1), основан на аналогичном аргументе сжатия, т. е. когда он выполняется, полугруппа системы взаимодействующих частиц действует как сжатие на подходящем пространство функций, снабженное нормой (так называемой тройной (полу)-нормой), управляющей колебаниями функции, причем полугруппа действует как стягивание в этой норме. Аналогично постановке единственности мер в постановке единственности Добрушина, также при критерии M<ε, получаются свойства сильного перемешивания единственной стационарной меры.
е. от любых начальных мер динамика во времени экспоненциально быстро сходится к уникальные стационарные меры. Этот критерий, так называемый «критерий M<ε» ([3], гл. 1), основан на аналогичном аргументе сжатия, т. е. когда он выполняется, полугруппа системы взаимодействующих частиц действует как сжатие на подходящем пространство функций, снабженное нормой (так называемой тройной (полу)-нормой), управляющей колебаниями функции, причем полугруппа действует как стягивание в этой норме. Аналогично постановке единственности мер в постановке единственности Добрушина, также при критерии M<ε, получаются свойства сильного перемешивания единственной стационарной меры.
В контексте вероятностных клеточных автоматов, а также в контексте динамики Глаубера показано, что критерий M<ε эквивалентен критерию единственности Добрушина для пространственно-временной меры Гиббса; см. [4,5].
1.2. Неравенства концентрации
Неравенства концентрации — это неравенства, в которых оценивается отклонение между функцией f=f(σ1,…,σn) n случайных величин σ1,…,σn и ее математическим ожиданием E(f). Идея состоит в том, что если функция слабо зависит от отдельных переменных σi, а распределение (σ1,…,σn) является произведением или близким к произведению, то вероятность отклонения f от E(f) становится очень малой. . Для измерения зависимости f отдельных координат рассматривается, например, колебание
Идея состоит в том, что если функция слабо зависит от отдельных переменных σi, а распределение (σ1,…,σn) является произведением или близким к произведению, то вероятность отклонения f от E(f) становится очень малой. . Для измерения зависимости f отдельных координат рассматривается, например, колебание
Важным примером неравенства концентрации является так называемая граница концентрации Гаусса.
где C>0 — константа, не зависящая от f и, в частности, не зависящая от n. Например, если f(σ)=1n∑i=1nσi и σi∈{−1,1}, то δif=2/n, и мы находим верхнюю границу 2e−Cnε2/4 для всех n≥1. Сила концентрационных неравенств типа (1) заключается в том, что они справедливы для общего f, т. е. далеко за пределами эмпирических средних значений.
Неравенства концентрации в контексте мер Гиббса для решеточных спиновых систем изучались в нескольких работах. В частности, в [6] автор доказывает неравенство типа (1) по критерию единственности Добрушина. См. [7] для недавнего обзора неравенств концентрации в контексте мер Гиббса.
См. [7] для недавнего обзора неравенств концентрации в контексте мер Гиббса.
1.3. Концентрация и уникальность
Центральный вопрос этой статьи заключается в следующем. Предположим, что мера Гиббса, связанная с данным потенциалом, удовлетворяет гауссовой границе концентрации, т. е. неравенству типа (1). Можем ли мы тогда заключить, что это единственная мера Гиббса, т. е. что фазового перехода нет?
В этой статье мы ограничимся трансляционно-инвариантными мерами Гиббса (т. е. так называемыми состояниями равновесия), но в очень общей постановке. Следуя [8], мы начали в [9] изучение связи между гауссовской границей концентрации и единственностью состояний равновесия в контексте спиновых систем на решетке Zd, где спин в каждом узле решетки принимает конечное число значений. Примеры включают модель Изинга при высокой температуре. Обратите внимание, что для этой модели при низкой температуре в d ≥ 2 происходит фазовый переход, а вероятности больших отклонений намагниченности подобны поверхности, а не объему. Это проявление фазового перехода исключает гауссовский предел концентрации, при котором все эргодические средние имеют объемные вероятности больших отклонений.
Это проявление фазового перехода исключает гауссовский предел концентрации, при котором все эргодические средние имеют объемные вероятности больших отклонений.
Здесь мы показываем единственность состояний равновесия при неравенстве типа (1), а затем обобщаем как контекст концентрационного неравенства, так и контекст мер Гиббса, показывая единственность в контексте так- называются наборами с нулевой информацией. Важным результатом в контексте состояний равновесия является вариационный принцип, который подразумевает, что относительная плотность энтропии между двумя состояниями равновесия равна нулю. Поэтому, если можно показать строго положительную нижнюю границу относительной плотности энтропии, получается единственность состояний равновесия. Набор состояний равновесия, связанных с данным трансляционно-инвариантным потенциалом, является частным случаем набора, в котором относительная плотность энтропии между двумя элементами набора всегда равна нулю. Мы называем такое множество множеством с нулевой информацией и обобщаем наши результаты уникальности на этот контекст, который включает, например, преобразования мер Гиббса и стационарные меры некоторых взаимодействующих систем частиц.
1.4. Содержание и организация статьи
Как показано выше, мы получаем нижнюю границу для нижней относительной плотности энтропии в терминах естественного расстояния между трансляционно-инвариантными вероятностными мерами, напоминающую и в духе результатов Бобкова и Гётце [10]. ], который доказал (в другой обстановке) нижнюю границу относительной энтропии в терминах квадрата расстояния Вассерштейна. Поскольку мы работаем в термодинамическом пределе пространства-произведения и интересуемся трансляционно-инвариантными вероятностными мерами, в конфигурационном пространстве нет трансляционно-инвариантного расстояния, для которого мы можем применить теорему Бобкова-Гётце. Мы можем избежать этой проблемы, введя подходящее расстояние для трансляционно-инвариантных вероятностных мер (а не для конфигураций).
Мы начнем с доказательства нижней границы нижней относительной плотности энтропии в контексте систем спинов общей решетки с пространством состояний Ω=SZd, где отдельные спины принимают значения в метрическом пространстве S ограниченного диаметра.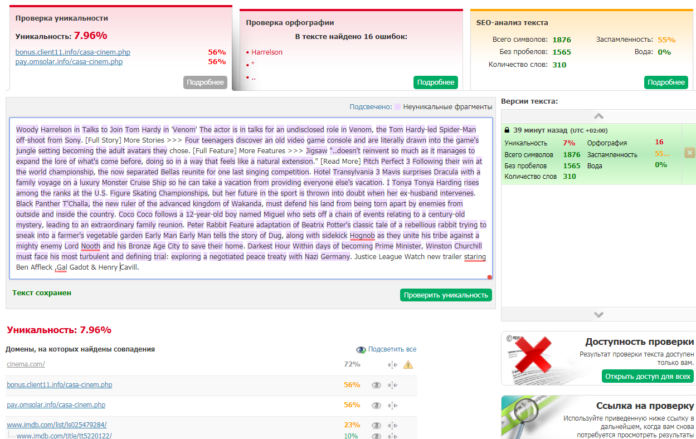 Свойство ограниченного диаметра позволяет связать квазилокальную функцию f с естественной последовательностью колебаний δif,i∈Zd, где δif представляет максимальное влияние на функцию f изменения спина в узле i. В заключительном разделе этой статьи мы даем обобщение этого, допуская более абстрактные односпиновые пространства и более общие связанные последовательности колебаний.
Свойство ограниченного диаметра позволяет связать квазилокальную функцию f с естественной последовательностью колебаний δif,i∈Zd, где δif представляет максимальное влияние на функцию f изменения спина в узле i. В заключительном разделе этой статьи мы даем обобщение этого, допуская более абстрактные односпиновые пространства и более общие связанные последовательности колебаний.
Остальная часть нашей статьи организована следующим образом. В разделе 2 мы вводим основные положения систем спинов решетки и важных функциональных пространств. В разделе 3 мы вводим гауссову границу концентрации, относительную энтропию (плотность), а также формулируем и доказываем наш основной результат в контексте односпинового пространства конечного диаметра. В разделе 4 мы обсуждаем приложения нашего результата к множествам с нулевым информационным расстоянием, включая, например, множество состояний равновесия относительно абсолютно суммируемых трансляционно-инвариантных потенциалов. В разделе 5 мы рассматриваем обобщение, вводя абстрактную последовательность колебаний, связанную с ней гауссовскую границу концентрации и состояние, и доказываем аналог нашего основного результата в этом обобщенном контексте.
2. Настройка
2.1. Конфигурационное пространство и оператор трансляции
Начнем со стандартного борелевского пространства (S,b) с метрикой dS и положим diam(S)=sups,s′∈SdS(s,s′). (Измеримое пространство (S,b) называется стандартным борелевским, если существует метрика на S, которая делает его полным сепарабельным метрическим пространством, и тогда b обозначает ассоциированную борелевскую σ-алгебру.) В дальнейшем для удобства обозначений , мы опускаем символ b и называем S стандартным борелевским пространством, где мы всегда предполагаем, что ассоциированная σ-алгебра является борелевской σ-алгеброй b.
Предположим, что diam(S)<∞. Позже, в разделе 5, мы покажем, как ослабить это предположение.
Это пространство S представляет собой “односпиновое пространство”, т.е. мы будем рассматривать конфигурации спинов решетки, в которых отдельные “спины” принимают значения в S. Обозначим через (ΩΛ,bΛ) пространство произведений (SΛ,∏i∈ Λbi), а (Ω,B) — конфигурационное пространство спинов решетки (ΩZd,bZd). Оборудуем это пространство топологией продукта. Элементы Ω называются конфигурациями. Для η∈Ω обозначим через ηi∈S его оценку в узле i∈Zd. Под σΛ мы понимаем элемент из ΩΛ, а под ηΛξΛc — конфигурацию, совпадающую с η на Λ и с ξ на Λc. Обозначим через S множество конечных подмножеств Zd.
Оборудуем это пространство топологией продукта. Элементы Ω называются конфигурациями. Для η∈Ω обозначим через ηi∈S его оценку в узле i∈Zd. Под σΛ мы понимаем элемент из ΩΛ, а под ηΛξΛc — конфигурацию, совпадающую с η на Λ и с ξ на Λc. Обозначим через S множество конечных подмножеств Zd.
Обозначим через τi:Zd→Zd, i∈Zd, карту, которая сдвигается или сдвигается на i; т. е. τi(j)=j+i, j∈Zd, а для Λ⊂Zd мы пишем τi(Λ)=Λ+i={j∈Zd:j=k+i,k∈Λ}, Λ ⊂Зд. Определим оператор сдвига, действующий на конфигурации, следующим образом (и используем тот же символ). Для каждого i∈Zd (τiσ)j=σj−i для всех j∈Zd. Это соответствует переводу σ вперед на i. Этим же символом обозначим оператор сдвига, действующий на функцию f:Ω→R. Для каждого i∈Zd функция τif определяется как τif(σ)=f(τiσ). Вероятностная (борелевская) мера на Ω является трансляционно-инвариантной, если для всех B∈B и для всех i∈Zd выполняется µ(τiB)=µ(B).
Обозначим через Pτ(Ω) множество трансляционно-инвариантных вероятностных мер на Ω.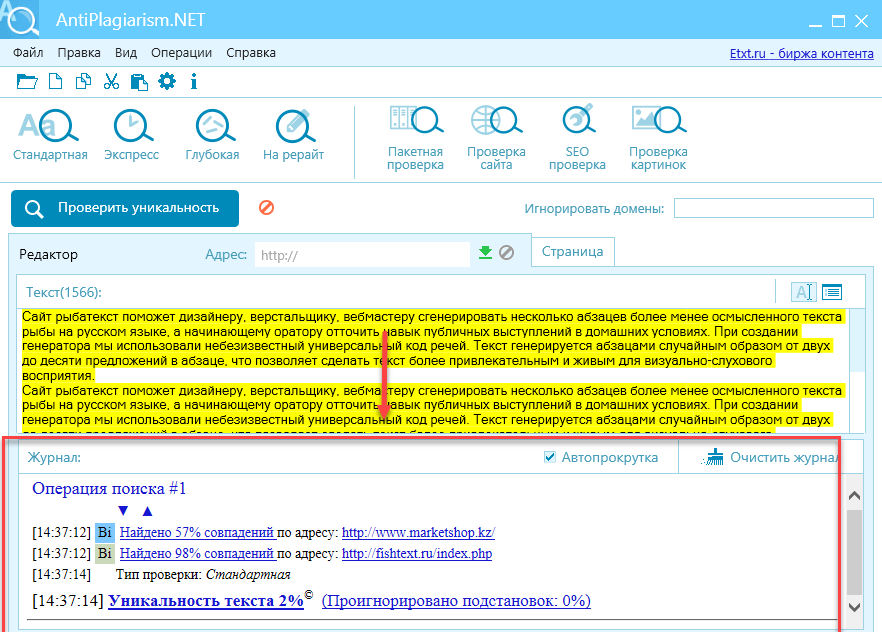 Обозначим через C(Ω),Cb(Ω) пространство непрерывных, соответственно ограниченных, непрерывных вещественнозначных функций на Ω.
Обозначим через C(Ω),Cb(Ω) пространство непрерывных, соответственно ограниченных, непрерывных вещественнозначных функций на Ω.
2.2. Локальные колебания и функциональные пространства
Непрерывной функции f:Ω→R мы связываем «последовательность» «локальных колебаний», δf:=(δif)i∈Zd, определяемую через
Позже, в разделе 5, в котором мы рассматриваем случай, когда S может иметь бесконечный диаметр, мы рассмотрим более абстрактное определение δf. В случае, когда S имеет конечный диаметр, (2) является наиболее естественным выбором.
Для целого числа p≥1 определим обычную ℓp-норму δf, ∥δf∥pp=∑i∈Zd(δif)p и ∥δf∥∞=supi∈Zdδif.
Мы называем непрерывную функцию локальной, если δif≠0 для конечного числа i∈Df⊂Zd. Набор Df тогда называется набором зависимостей f. Обозначим через L(Ω) множество локальных непрерывных функций на Ω.
Мы называем непрерывную функцию квазилокальной, если она является равномерным пределом последовательности локальных непрерывных функций. Если S компактно, то по теореме Стоуна–Вейерштрасса локальные непрерывные функции равномерно плотны в C(Ω).
Если S компактно, то по теореме Стоуна–Вейерштрасса локальные непрерывные функции равномерно плотны в C(Ω).
Обозначим через QL(Ω) пространство всех непрерывных квазилокальных функций на Ω.
Для 1≤p≤∞ введем пространства
Будем говорить, что µn→µ, если для всех ограниченных непрерывных локальных функций выполняется ∫fdµn→∫fdµ (тогда по определению квазилокальности то же верно для ограниченных непрерывных квазилокальных функций). Это индуцирует так называемую слабую квазилокальную топологию на вероятностных мерах. Заметим, что в нашем случае, когда по предположению односпиновое пространство S является полным сепарабельным метрическим пространством, эта топология совпадает с обычной слабой топологией; см. [11] (стр. 898).
В нашем случае множество ограниченных квазилокальных непрерывных функций является мероразделяющим, т. е. для двух вероятностных мер µ≠µ′ существует ограниченная квазилокальная непрерывная функция f такая, что
Поскольку по определению ограниченные непрерывные квазилокальные функции могут быть равномерно аппроксимированы ограниченными непрерывными локальными функциями, если множество ограниченных квазилокальных функций является мероразделяющим, то множество ограниченных непрерывных локальных функций также является мероразделяющим. Следовательно, в наших условиях для двух вероятностных мер µ≠µ′ существует ограниченная локальная f (не постоянная), такая, что
Следовательно, в наших условиях для двух вероятностных мер µ≠µ′ существует ограниченная локальная f (не постоянная), такая, что
Это можно увидеть следующим образом. Если µ≠µ′, то существует ограниченное замкнутое цилиндрическое множество A⊂Ω такое, что µ(A)≠µ′(A), поскольку борелевская σ-алгебра на Ω порождается такими множествами. Индикатор этого множества можно аппроксимировать ограниченными локальными непрерывными функциями как в L1(µ), так и в L1(µ′).
3. Гауссов предел концентрации и относительная энтропия
3.1. Абстрактная граница концентрации по Гауссу
Теперь мы можем дать определение границы концентрации по Гауссу в наших условиях.
Следующее предложение утверждает, что (5) автоматически распространяется на более широкий класс функций.
3.2. Относительная энтропия
Для вероятностной меры µ через µΛ обозначим ее ограничение на подалгебру BΛ=σ{ηi,i∈Λ}, порожденную проекцией pΛ:Ω→ΩΛ. Мы также обозначаем через BΛ множество ограниченных BΛ-измеримых функций из Ω в R.
Мы также обозначаем через BΛ множество ограниченных BΛ-измеримых функций из Ω в R.
Для двух вероятностных мер µ,µ′ на Ω и Λ∈S определим относительную энтропию µ′ относительно µ равенством
Обозначим далее через (Λn)n∈N последовательность «кубов» Λn=[−n,n]d∩Zd, n李1.
Имеем следующую вариационную характеристику относительной энтропии (доказательство см., например, в [13] (стр. 100))
где супремум берется по всем BΛ-измеримым функциям таким, что ∫efdµΛ<∞.
3.3. Основной результат
В приведенной ниже основной теореме мы доказываем, что из гауссовой границы концентрации следует строгая положительность нижней относительной плотности энтропии. Вводя соответствующую метрику на множестве вероятностных мер, мы показываем, что нижняя относительная плотность энтропии ограничена снизу константой, умноженной на квадрат этого расстояния. Этот результат существенно обобщает соответствующий результат из [9], где существенна конечность односпинового пространства. Кроме того, доказательство проще и основано на вариационной формуле для относительной энтропии в сочетании с квадратичной оценкой функции, производящей логарифмический момент, исходя из предполагаемой гауссовой границы концентрации.
Этот результат существенно обобщает соответствующий результат из [9], где существенна конечность односпинового пространства. Кроме того, доказательство проще и основано на вариационной формуле для относительной энтропии в сочетании с квадратичной оценкой функции, производящей логарифмический момент, исходя из предполагаемой гауссовой границы концентрации.
Определенная выше метрика порождает квазилокальную топологию, поэтому сходимость по этой метрике влечет слабую сходимость. В самом деле, сходимость µn→µ в метрике d, очевидно, влечет ∫fdµn→∫fdµ для всех локально непрерывных f, а значит, и для всех квазилокальных непрерывных f. Последнее влечет µn→µ в квазилокальной топологии, что совпадает со слабой топологией.
Теперь мы можем сформулировать наш основной результат.
Начнем с леммы из [7]. Для удобства читателя мы повторим здесь краткое доказательство.
Следующее следствие показывает, что сходимость по относительной плотности энтропии подразумевает сходимость по расстоянию d.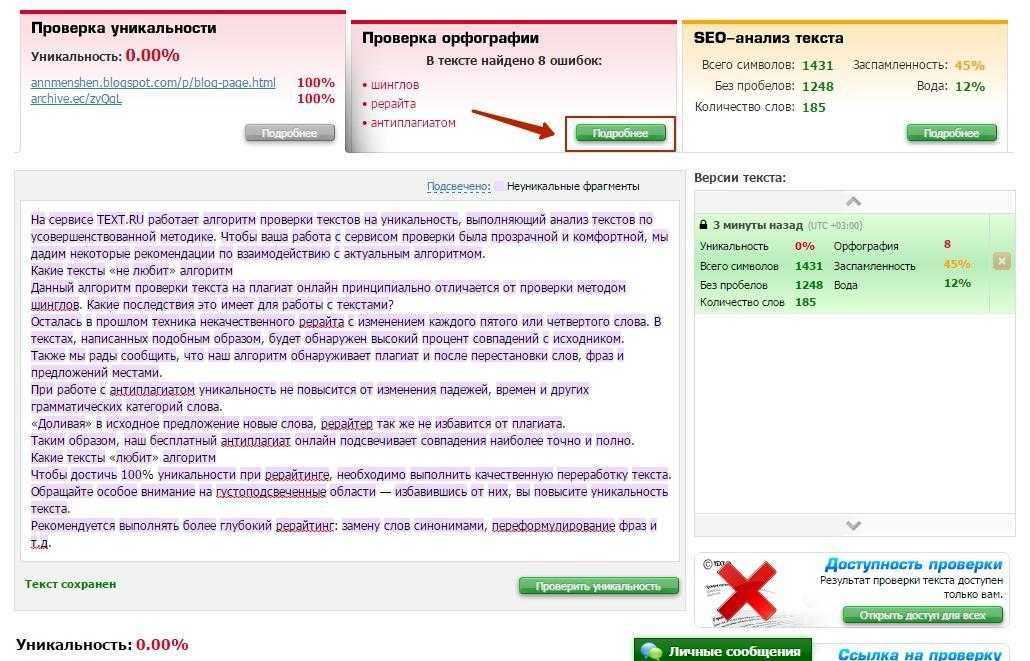 Это можно использовать для стохастической динамики, если можно показать, что относительная плотность энтропии сходится. См. раздел приложений ниже для некоторых примеров.
Это можно использовать для стохастической динамики, если можно показать, что относительная плотность энтропии сходится. См. раздел приложений ниже для некоторых примеров.
Мы завершаем этот раздел двумя дополнительными замечаниями, касающимися нашего результата с критерием Бобкова-Гётце.
4. Приложения: единственность состояний равновесия и не только трансляционно-инвариантных мер Гиббса, связанных с абсолютно суммируемым потенциалом. Затем мы рассмотрим обобщения и модификации таких множеств.
4.1. Уникальность равновесных состояний
В этом подразделе мы кратко познакомим вас с необходимыми основами мер Гиббса. Читатель, знакомый с теорией меры Гиббса, может пропустить этот подраздел. Читатель может обратиться к [1] (особенно глава 16) или [11] (глава 2) для получения дополнительной информации о формализме Гиббса.
Пусть λ — вероятностная мера на S, а для λΛ(dσΛ)=⊗i∈Λλ(dσi) — соответствующая мера произведения на SΛ. Мера λ называется «априорной» мерой на S с ассоциированной с ней априорной мерой ⊗i∈Zdλ(dσi) на Ω.
Мера λ называется «априорной» мерой на S с ассоциированной с ней априорной мерой ⊗i∈Zdλ(dσi) на Ω.
Равномерно абсолютно суммируемый трансляционно-инвариантный потенциал мы называем функцией
со следующими свойствами:
- (a)
Локальность: для всех A∈S U(A,·) BA-измерима и непрерывна.
- (б)
Абсолютная суммируемость: ∑A∋0∥U(A,·)∥∞<∞.
- (c)
Трансляционная инвариантность: U(A+i,τiσ)=U(A,σ) для всех σ∈Ω, A∈S.
Назовем U множеством равномерно абсолютно суммируемых трансляционно-инвариантных потенциалов. Затем строим локальные меры Гиббса с краевым условием ξ∈Ω. Для конечного подмножества Λ∈S мера Гиббса в объеме Λ с граничным условием ξ вне Λ определяется через
где HΛξ — гамильтониан в объеме Λ с краевым условием ξ:
и где ZΛξ — нормировка
Семейство (γΛ(dσΛ|·))Λ∈S называется спецификацией Гиббса, связанной с потенциалом U (с априорной мерой λ).
Ввиду равномерной абсолютной суммируемости U автоматически получаем, что для всех f, локальных и непрерывных, функция ξ↦∫f(σΛξΛc)γΛ(dσΛ|ξ) квазилокальна и непрерывна. Мы говорим, что спецификация γΛ(·|·) квазилокальна.
Тогда мы называем меру Гиббса µ с потенциалом U (и априорную меру λ), если γΛ(dσΛ|ξ) согласуется с мерами Гиббса конечного объема, т. е. если для всех f:Ω→R ограничено и измеримо, и Λ∈S, имеем
для µ-почти каждого ξ.
Обозначим через Gτ(U) множество трансляционно-инвариантных мер Гиббса, ассоциированных с потенциалом U. Эти меры называются «состояниями равновесия», ассоциированными с U.
Из вариационного принципа ([1], гл. 16) следует, что если µ,ν∈Gτ(U), то s*(µ|ν)=s*(ν|µ)=0, и наоборот, если µ∈Gτ(U) и ν∈Pτ, таково, что s*(ν |µ)=0, то ν∈Gτ(U). Тогда как следствие теоремы 1 мы получаем следующий результат:
Это существенно расширяет импликацию между GCBC и единственностью состояний равновесия из [9]. ], где мы рассматривали только конечные односпиновые пространства S.
], где мы рассматривали только конечные односпиновые пространства S.
4.2. Наборы с нулевым информационным расстоянием
Пример набора состояний равновесия из предыдущего подраздела естественным образом ведет к более общему понятию «множества с нулевым информационным расстоянием», определенному ниже.
Тогда из теоремы 1 сразу получаем следующее предложение.
Мы приводим еще четыре примера (помимо состояний равновесия) таких наборов расстояний с нулевой информацией, иллюстрирующих предложение 3.
- (a)
Асимптотически несвязанные меры и Πf-совместимые меры.
Первое обобщение гиббсовского контекста дается в области «асимптотически разделенных мер» через понятие Πf-совместимых мер, см. [16]. Этот параметр выходит за рамки квазилокальных спецификаций и поэтому включает множество соответствующих примеров негиббсовских мер.
В этой постановке множество Πf-совместимых мер (связанных с локальной функцией f) является множеством с нулевой информацией (см.
 [16, теорема 4.1]), и поэтому, если это множество содержит элемент µ, удовлетворяющий GCBC, то он совпадает с одноэлементным {µ}.
[16, теорема 4.1]), и поэтому, если это множество содержит элемент µ, удовлетворяющий GCBC, то он совпадает с одноэлементным {µ}.- (б)
Ренормализационные групповые преобразования мер Гиббса.
Другой важный класс примеров следующий. Мы говорим, что преобразование T:Pτ(Ω)→Pτ(Ω′) сохраняет множества расстояний с нулевой информацией, если множество расстояний с нулевой информацией отображается с помощью T в множество расстояний с нулевой информацией. Важными примерами таких преобразований T являются локальные и трансляционно-инвариантные преобразования ренормализационной группы, изучавшиеся в [11, раздел 3.1, стр. 9].60, условия Т1-Т2-Т3. Примеры таких преобразований включают усреднение блочного спина, прореживание и стохастические преобразования, такие как преобразование Каданова. Поскольку преобразования являются «локальными и трансляционно-инвариантными ядрами вероятностей», сразу следует свойство s*(µT|νT)≤s*(µ|ν).
В этом случае из предложения 3 следует, что если U∈U, µ∈Gτ(U) — ассоциированная трансляционно-инвариантная мера Гиббса, а µT удовлетворяет GCBC для некоторого C∈(0,∞), то ν=µT для всех ν, такое что s*(ν|µT)=0.
 В частности, отсюда следует, что µ′T=µT для всех µ′∈Gτ(U). Действительно, в этом случае s*(µ′T|µT)≤s*(µ′|µ)=0.
В частности, отсюда следует, что µ′T=µT для всех µ′∈Gτ(U). Действительно, в этом случае s*(µ′T|µT)≤s*(µ′|µ)=0.Обратите внимание, что µT может быть негиббсовским; следовательно, импликация ν=µT для всех ν, для которых s*(ν|µT)=0, не может быть получена из вариационного принципа.
- (c)
Проекции мер Гиббса.
Пусть µ — трансляционно-инвариантная мера Гиббса на пространстве состояний SZd (связанная с трансляционно-инвариантным потенциалом), которая удовлетворяет GCBC для некоторого C∈(0,∞). Пусть для d′
Как следствие, если µd′ является мерой Гиббса трансляционно-инвариантного потенциала Ud′′, то этот потенциал Ud′′ не имеет других трансляционно-инвариантных мер Гиббса.
 Это дает единственность для набора мер Гиббса, где потенциал определяется только неявно и может быть сложным, т. Е. Единственность не является следствием простого критерия.
Это дает единственность для набора мер Гиббса, где потенциал определяется только неявно и может быть сложным, т. Е. Единственность не является следствием простого критерия.Проекции мер Гиббса естественным образом возникают в контексте вероятностных клеточных автоматов, где стационарные меры являются проекциями пространственно-временных мер Гиббса [4]. В этом случае результат говорит нам, что если пространственно-временная мера удовлетворяет GCBC для некоторого C>0, то единственная стационарная мера, если Гиббс, имеет потенциал с уникальным состоянием равновесия. Проекции мер Гиббса могут не быть гиббсовскими, как показано в [17] для проекции низкотемпературной модели Изинга при d=2 на ось X. Это открытая и интересная проблема, чтобы исследовать, удовлетворяет ли эта спроектированная мера гауссовой границе концентрации.
- (d)
Стационарные меры для изинговской спиновой динамики Глаубера.
Дополнительным примером набора расстояний с нулевой информацией является набор стационарных и трансляционно-инвариантных мер для (изинговского спина, т.
 мера как стационарная мера; см. [18], раздел 4. См. также [19,20] более ранние результаты в постановке обратимой глауберовской динамики и [21] недавние результаты в том же духе для более общей локальной динамики. Как следствие предложения 3, мы заключаем, что если существует трансляционно-инвариантная мера Гиббса ν как стационарная мера и существует трансляционно-инвариантная стационарная мера µ, удовлетворяющая GCBC для некоторого C>0, то µ=ν совпадают, и µ – единственная трансляционно-инвариантная стационарная мера. Более того, если в этой постановке можно показать, что, начиная динамику с трансляционно-инвариантной начальной меры µ и обозначая µt для меры в момент времени t>0, мы имеем S*(µt|ν)→0 при t→ ∞, то из следствия 1 получаем, что µt→ν при t→∞ в смысле расстояния (7).
мера как стационарная мера; см. [18], раздел 4. См. также [19,20] более ранние результаты в постановке обратимой глауберовской динамики и [21] недавние результаты в том же духе для более общей локальной динамики. Как следствие предложения 3, мы заключаем, что если существует трансляционно-инвариантная мера Гиббса ν как стационарная мера и существует трансляционно-инвариантная стационарная мера µ, удовлетворяющая GCBC для некоторого C>0, то µ=ν совпадают, и µ – единственная трансляционно-инвариантная стационарная мера. Более того, если в этой постановке можно показать, что, начиная динамику с трансляционно-инвариантной начальной меры µ и обозначая µt для меры в момент времени t>0, мы имеем S*(µt|ν)→0 при t→ ∞, то из следствия 1 получаем, что µt→ν при t→∞ в смысле расстояния (7).
5. Обобщение
В условиях раздела 2.1 без дополнительного предположения о конечности диаметра S определение колебания f в (2) уже не подходит. В самом деле, становится естественным включать неограниченные функции, что делает (2) бесконечным. Рассмотрим, например, S=R и Ω=SZd, снабженные произведением гауссовских мер, тогда функция f(η)=ηi должна быть возможным выбором. Рассмотрим теперь общий стандартный борелевский S, который таков, что для пространства произведений Ω=SZd квазилокальные ограниченные функции являются мероразделяющими.
Рассмотрим, например, S=R и Ω=SZd, снабженные произведением гауссовских мер, тогда функция f(η)=ηi должна быть возможным выбором. Рассмотрим теперь общий стандартный борелевский S, который таков, что для пространства произведений Ω=SZd квазилокальные ограниченные функции являются мероразделяющими.
Чтобы продолжить, свяжем с функцией f:Ω→R абстрактную последовательность колебаний δf=(δif)i∈Zd, удовлетворяющую следующим условиям.
- 1.
Трансляционная инвариантность: (δ(τif))j=δi+jf, i,j∈Zd.
- 2.
Невырожденность: δif равно нулю для функции f тогда и только тогда, когда f не зависит от i-й координаты, т. е. δif=0 тогда и только тогда, когда для всех η,σ таких, что ηj=σj для всех j≠i, f(η)=f(σ).
- 3.
Монотонность: для ξ∈Ω и f ограниченной квазилокальной функции мы рассматриваем локальную аппроксимацию f, заданную выражением
Затем мы требуем, чтобы для всех ξ, для всех Λ и для всех i∈Zd δifΛ,ξ ≤δ, если.

- 4.
Однородность первой степени: δi(βf)=|β|δif для всех β∈R и для всех i∈Zd.
Обратите внимание, что из условия 3 следует, что для заданных f, ξ, Λ⊂Λ′ и i∈Zd выполняется δifΛ,ξ≤δifΛ′,ξ. В самом деле, заметим, что (fΛ′,ξ)Λ,ξ=fΛ,ξ для Λ⊂Λ′
. Наиболее естественным примером, отличным от (2), является
В более общем виде можно определить
где ψ:S×S→[0,∞) удовлетворяет условию ψ(s,s′)=0 тогда и только тогда, когда s=s′.
Для заданной последовательности колебаний δ функция называется δ-липшицевой, если supi∈Zdδif<∞. Затем мы вводим
Тогда мы имеем следующий аналог теоремы 1. Поскольку доказательство следует точно таким же шагам, что и доказательство теоремы 1, мы предоставляем его читателю.
В заключение отметим, что тот факт, что мы выбрали группу Zd, сделан для простоты.






 Так времени можно будет истратить меньше, а результат получить гораздо выше.
Так времени можно будет истратить меньше, а результат получить гораздо выше. [16, теорема 4.1]), и поэтому, если это множество содержит элемент µ, удовлетворяющий GCBC, то он совпадает с одноэлементным {µ}.
[16, теорема 4.1]), и поэтому, если это множество содержит элемент µ, удовлетворяющий GCBC, то он совпадает с одноэлементным {µ}.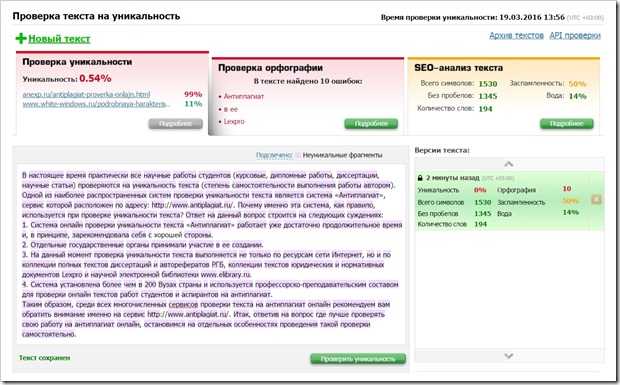 В частности, отсюда следует, что µ′T=µT для всех µ′∈Gτ(U). Действительно, в этом случае s*(µ′T|µT)≤s*(µ′|µ)=0.
В частности, отсюда следует, что µ′T=µT для всех µ′∈Gτ(U). Действительно, в этом случае s*(µ′T|µT)≤s*(µ′|µ)=0.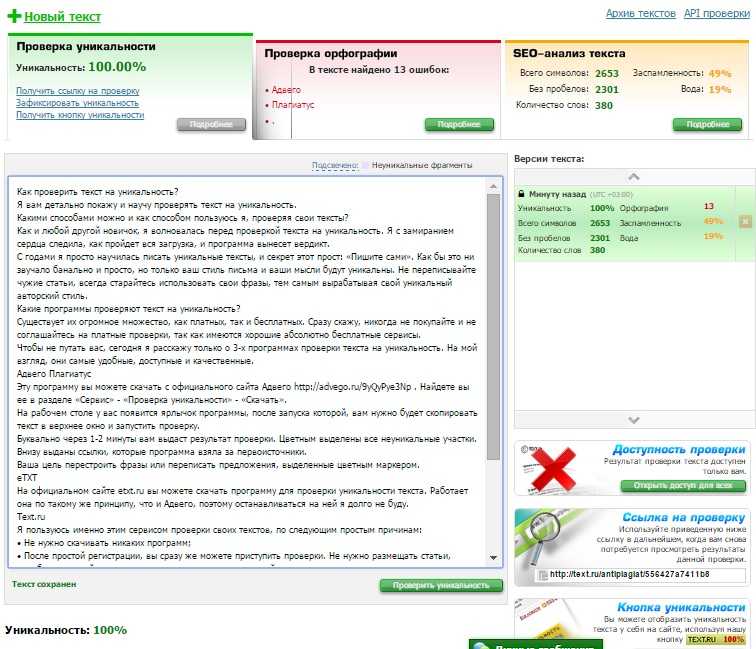 Это дает единственность для набора мер Гиббса, где потенциал определяется только неявно и может быть сложным, т. Е. Единственность не является следствием простого критерия.
Это дает единственность для набора мер Гиббса, где потенциал определяется только неявно и может быть сложным, т. Е. Единственность не является следствием простого критерия.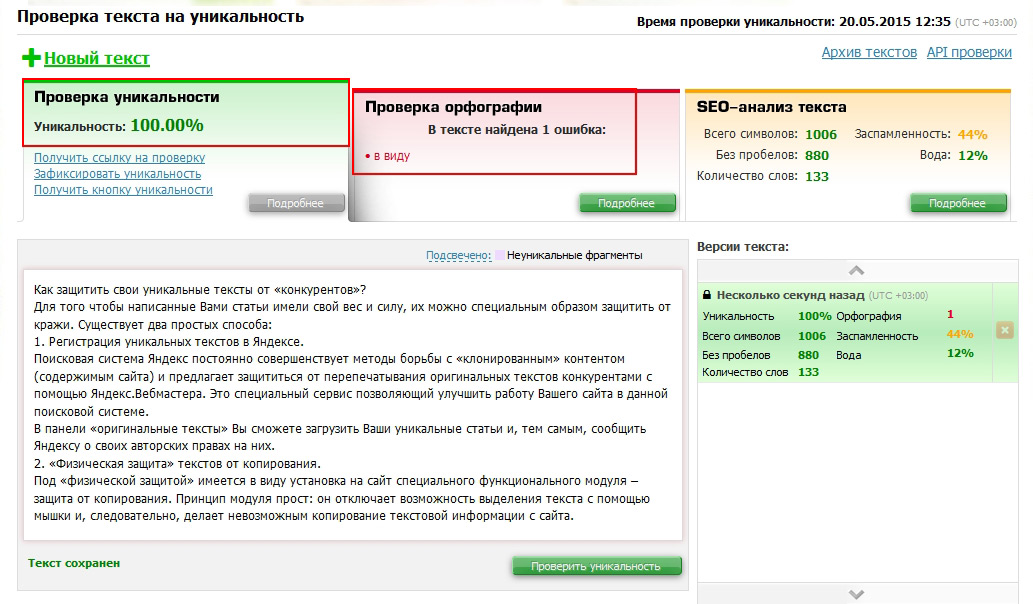 мера как стационарная мера; см. [18], раздел 4. См. также [19,20] более ранние результаты в постановке обратимой глауберовской динамики и [21] недавние результаты в том же духе для более общей локальной динамики. Как следствие предложения 3, мы заключаем, что если существует трансляционно-инвариантная мера Гиббса ν как стационарная мера и существует трансляционно-инвариантная стационарная мера µ, удовлетворяющая GCBC для некоторого C>0, то µ=ν совпадают, и µ – единственная трансляционно-инвариантная стационарная мера. Более того, если в этой постановке можно показать, что, начиная динамику с трансляционно-инвариантной начальной меры µ и обозначая µt для меры в момент времени t>0, мы имеем S*(µt|ν)→0 при t→ ∞, то из следствия 1 получаем, что µt→ν при t→∞ в смысле расстояния (7).
мера как стационарная мера; см. [18], раздел 4. См. также [19,20] более ранние результаты в постановке обратимой глауберовской динамики и [21] недавние результаты в том же духе для более общей локальной динамики. Как следствие предложения 3, мы заключаем, что если существует трансляционно-инвариантная мера Гиббса ν как стационарная мера и существует трансляционно-инвариантная стационарная мера µ, удовлетворяющая GCBC для некоторого C>0, то µ=ν совпадают, и µ – единственная трансляционно-инвариантная стационарная мера. Более того, если в этой постановке можно показать, что, начиная динамику с трансляционно-инвариантной начальной меры µ и обозначая µt для меры в момент времени t>0, мы имеем S*(µt|ν)→0 при t→ ∞, то из следствия 1 получаем, что µt→ν при t→∞ в смысле расстояния (7).