какой выбрать? – Блог – — Assorti-Market.ru
Это одна из самых популярных игрушек, в которую в детстве играли практически все, и в которую играют сейчас современные дети. В продаже можно встретить множество вариаций этой головоломки: начиная с детских облегченных вариантов, и заканчивая сложными геометрическими фигурами, для сборки которых, придется потратить не один час.
Сегодня мы рассмотрим и сравним различные виды Кубика Рубика, и поможем вам определиться с выбором.
Для начала, немного истории: Кубик Рубика (классический первоначальный размер был 3х3х3) был изобретен в 1974 году венгерским скульптором и преподавателем архитектуры Эрнё Рубиком. Причем к идее создания мировой головоломки он пришел совершенно случайно: Эрнё никак не мог втолковать своим студентам математическую теорию групп. Тогда он взял 27 маленьких деревянных кубиков и окрасил их в 6 разных цветов. Неожиданно для себя, Рубик понял, что сложить их в один куб, чтобы каждая грань была окрашена в свой цвет, было довольно сложно. Сам преподаватель сражался с этой задачей месяц!
Таким образом, Эрнё Рубиком была создана увлекательнейшая головоломка и учебное пособие в одном предмете. Последним и самым сложным шагом оставалось придумать механизм. И 30 января 1974 года Э. Рубик получает венгерский патент на свое изобретение «Волшебный Куб».
В начале 1980 года было решено переименовать изобретение из «Magic Cube» в «Rubick’s Cube». Именно в это время и начался настоящий бум и рассвет чудо-куба! Головоломка поступила в продажу по всему миру: люди скупали их моментально, это было похоже на настоящее помешательство. Венгрия не справлялась с производством кубов, и на рынке появилась море подделок. Венгрия могла производить не более нескольких миллионов штук в год, поэтому заводы начали открываться в Гонконге, Коста-Рике, Тайване и Бразилии.
Занимательные факты:
- Изначально Кубик Рубика рассматривался как учебное пособие для студентов.
- Число всех достижимых различных состояний Кубика Рубика 3x3x3 равно 43 252 003 274 489 856 000.
- В 80-ых годах было выпущено более 60 книг по сборке Кубика Рубика.
- Художники создавали произведения искусства из Кубиков Рубика.
- Существуют официальные соревнования по скоростной сборке Кубика.
- Действующий рекорд для кубика 3х3х3 — 4,904 сек
- Помимо классического куба существует множество других форм головоломки: пирамиды, шары, додекаэдры и проч.
- На данный момент самым большим «невиртуальным» Кубиком Рубика является кубик 13х13х13.
Ну а теперь рассмотрим Кубики Рубика, которые вы можете приобрести в нашем магазине.
1. Кубик Рубика 2х2 для детей
Это облегченный вариант
Купить Кубик Рубика 2х2 для детей

2. Кубик Рубика 2х2
Этот Кубик Рубика так же является облегченным вариантом, но посложнее чем детский. Если в детском Кубике Рубика грани окрашены лишь в два цвета, то в этом используется классический вариант: 6 граней — 6 цветов. Прекрасно подойдет для начинающих, а так же для тех юных гениев, что собрали детский вариант, и хотят перейти к более сложной головоломке!
Купить Кубик Рубика 2х2

3. Кубик Рубика 3х3 Классическая версия
Это классическая, первоначальная версия знаменитой головоломки. Именно в этом виде кубик был создан венгерским скульптором и архитектором Эрнё Рубиком. Идеально подойдет для всех возрастов. Собирать кубик можно как самому, полностью вовлекаясь в процесс разгадывания головоломки, как и по специальным формулам, чтобы отточить ловкость рук и скорость сборки. Данная модель изготовлена из качественного пластика, а поставляется вместе с оригинальной подставкой.
Купить Кубик Рубика 3х3 Классическая версия

4. Купить Кубик Рубика 3х3 Скоростной
Этот кубик для настоящего профессионала. Предназначен для супер-быстрой сборки. Как вы уже знаете, существуют соревнования по сборке Кубика Рубика, и именно эта модель пользуется популярностью у участников. Каждый элемент изготовлен максимально качественно, что позитивно отражается на скорости сборки.
Купить Кубик Рубика 3х3 Скоростной

5. Кубик Рубика 4х4
А вот и модель посложнее! Если вы в совершенстве овладели сборкой кубика версии 3х3, то вы просто обязаны перейти на новый уровень. Ведь у этой головоломки совершенно другие алгоритмы сборки, другие лазейки и уловки. Но этот кубик вам так же подойдет, если вы сразу хотите начать со сложного и хорошенько напрячь руки и мозги.
Купить Кубик Рубика 4х4

6. Кубик Рубика 5х5
Самая сложная головоломка из всей серии! Купить Кубик Рубика 5х5 стоит в обязательном порядке, если вы настоящий профессионал в сборке предыдущих легких версий, и хотите продвинуться на следующий уровень. Количество комбинаций и вариантов увеличивается, алгоритмы усложняются, а вместе с этим увеличивается время, которое вы потратите, сидя за этой моделью. Изготовлен из качественного пластика, в комплекте идет оригинальная подставка.
Купить Кубик Рубика 5х5

7. Башня Рубика
Необычная вариация головоломки. Представляет собой параллелепипед, со сторонами два и четыре кубика. Благодаря своей форме, башня намного сложнее классического кубика, поэтому поломать голову над ней придется не один час. Впервые Башня Рубика появилась в Японии, она настолько полюбилась японцам, что тут же стала популярна во всем мире.
Купить Башню Рубика

8. Змейка Рубика
Легкая и интересная головоломка для детей. Змейка состоит из 24 треугольников, которые вращаются, что позволяет создавать различные фигуры. Развивает моторику рук, фантазию и логику, такая змейка станет настоящей находкой для любознательного ребенка.
Купить Змейку Рубика

9. Кубик Рубика 3х3 VOID
Еще одна разновидность знаменитой головоломки. Представляет собой куб, полый внутри. Имеет совершенно другой механизм движений. VOID универсален: подойдет как новичкам, так и профессионалам складывания Кубика Рубика. Изготовлен из качественного, приятного на ощупь пластика.
Купить Кубик Рубика 3х3 VOID

10. Кубик Венеры
У этой модели принцип работы и механизм совершенно такой же, как и у классического Кубика. Разница лишь в форме — детали Кубика Венеры имеют разные причудливые формы. Расстояние между деталями сведено к минимуму. Прекрасная головоломка и для новичков, и для тех, кто захочет попробовать что-то еще, помимо классической версии.
Купить Кубик Венеры

11. Шестеренки со сдвигом
Необычная и оригинальная головоломка. Состоит не просто из граней, а из граней в виде шестеренок, вращающихся сразу в трех плоскостях. Невероятно занимательная игрушка, которая поможет развить логическое и пространственное мышление. Разгадывайте, крутите, находите пути сборки, создавая и записывая свои алгоритмы!
Купить Шестеренки со сдвигом

12. Шестеренчатый куб
Настоящая интеллектуальная головоломка! Имеет такой же принцип работы, как и у предыдущего куба: вращающиеся шестеренки. Но собирается этот кубик значительно легче, чем обычный Кубик Рубика, так что прекрасно подойдет для новичков и детей. Развивает пространственное мышление и моторику рук
.Шестеренчатый куб

13. Магия Рубика
Самая нестандартная головоломка из нашего ассортимента. Представляет собой пластину из 8 квадратных панелей, размером 4х2. Правильно собранная головоломка образует рисунок из трех соединенных и трех разъединенных колец. Принцип работы очень прост: все панели связаны между собой особой леской, что позволяет перемещать панели, как вам угодно. Складывать, раскладывать, гнуть, сворачивать. Самое важное в использовании данной игрушки: если вы чувствуете натяжение лески, лучше попробовать сложить игру в другом направлении, где процесс происходит мягче.
Купить Магию Рубика

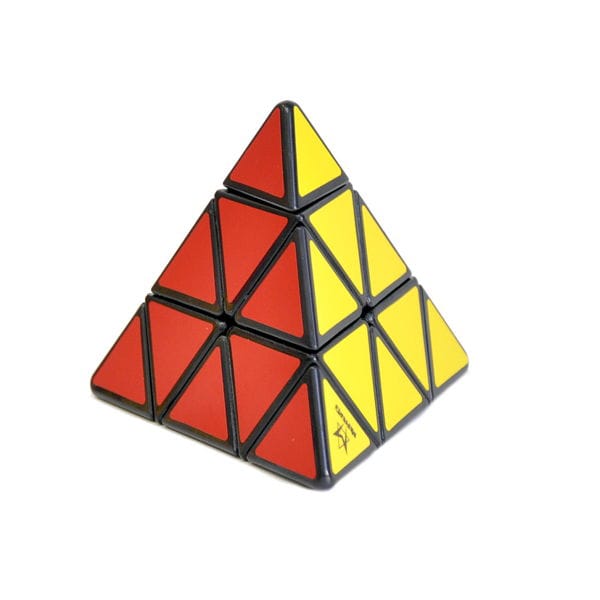
14. Пирамида Рубика (Пирамидка Мефферта)
Прекрасный тренажер для мозгов в виде пирамидки. Головоломка представляет собой пирамиду с 4 сторонами, каждая окрашена в свой цвет. Подойдет для начинающих, так как собрать Пирамиду Мефферта гораздо проще, чем классический Кубик Рубика.
Купить Пирамида Рубика (Пирамидка Мефферта)
Головоломки — отличный способ с пользой и удовольствием провести время. Дома, в дороге, на работе — осталось лишь выбрать и купить Кубик Рубика, подходящий именно для вас!
История кубика Рубика — Лаборатория Игр
| |
| «Тот факт, что каждая грань куба состоит из трёх слоев по три блока, имеет большое значение. Число три, кажется, обладает специфическим смыслом, выражающимся в некоторых странных связях между человеком и природой. Мать — Дитя — Отец. Небеса — Земля — Преисподняя. Создание — Сохранение — Разрушение. Рождение — Жизнь — Смерть«. Эрно Рубик |
| Число возможных различных состояний кубика Рубика равно (8! х 38-1) х (12! х 212-1)/2 = 43 252 003 274 489 856 000, т.е. более 43 квинтиллионов комбинаций. Несмотря на это, теоретически из любого состояния головоломку можно собрать за 22 хода — так называемый «алгоритм Господа». Задача поиска оптимального (по числу ходов) алгоритма является самой сложной и не решенной пока математической задачей, связанной с Кубиком Рубика. Первые Кубики сопровождались следующей аннотацией: «Эта игрушка развивает логическое мышление и стереоскопическое зрение у детей и взрослых. Синхронная манипуляция на многих поверхностях является очень сложным заданием, которое можно решить только при условии открытия логики поворотов». Все права на любое трехмерное воспроизведение, и даже на любое графическое или экранное представление этого объекта, остаются за Эрно Рубиком и будут актуальны вплоть до истечения 70 лет со дня смерти создателя гениального шедевра. |
В 1974 году 29-летний Эрно Рубик (Erno Rubik), в будущем первый официальный миллионер восточно-европейского социалистического блока, а тогда обычный молодой преподаватель живущий в одной квартире с родителями, трудился на факультете интерьерного дизайна (Department of Interior Design) будапештской Академии прикладных искусств и ремесел (Academy of Applied Arts and Crafts).
Он преподавал венгерским студентам промышленный дизайн и архитектуру. Увлекался также геометрией и трёхмерным предметным моделированием, находя его идеальным средством для развития в учащихся навыков пространственного воображения. Как это обычно и бывает с выдающимися изобретениями, проект кубика вынашивался не один год. В начале изобретение представляло собой набор из 27 деревянных кубиков с разноцветными гранями (всего 27 х 6=156 цветных граней).
По одной из версий, при помощи данного учебного пособия Рубик пытался втолковать непонятливым воспитанникам основы математической теории групп. Задача изобретателя была такова: заставить отдельные разноцветные кубики свободно вращаться на своих местах, не нарушая конструктивного единства всего приспособления.
Финальный прототип кубика Рубика. Источник: Beyond Rubik’s Cube.
В дальнейшем пришлось отбросить всё лишнее: в своем первом кубике Рубик оставил всего 54 внешние грани: одноцветные у шести центральных кубиков, двухцветные у двенадцати боковых, и трёхцветные у восьми угловых. Ровно в таком виде мы и видим кубик Рубика сейчас. На вакантное место единственного «внутреннего» кубика был помещен цилиндрический скрепляющий механизм, который был прочно связан со всеми наружными кубиками, но позволял им свободно вращаться друг относительно друга. Так из учебного пособия, кубик Рубика стал игрушкой!
В качестве первоиспытателей головоломки выступали друзья Рубика и студенты Академии. Поскольку культуры предпринимательства в коммунистической Венгрии не было, желание запатентовать конструкцию пришло в голову к Рубику только через некоторое время.
В 1975-м Рубик получил венгерский патент на своё изобретение. Однако выпуск опытной промышленной партии состоялся лишь в конце 1977-го. Первым производителем кубика был небольшой будапештский кооператив, выпустивший кубик как новогоднюю игрушку под Рождество 1978 года. Это был добротно сделанный под названием «Волшебный Кубик» (Buvuos Kocka) в красочной упаковке, единичные экземпляры которого появились и в СССР. До всемирного триумфа самой продаваемой в истории головоломки, которую держал в руках каждый восьмой житель планеты, кубику Рубика было ещё очень и очень далеко. Дело в том, что выпускавшийся с конца 1977-го в Венгрии ограниченным тиражом кубик Рубика далеко не сразу завоевал Запад.
Не исключено, что события и дальше развивались бы с черепашьей скоростью, если бы игрушкой не заинтересовался некто Тибор Лакзи (Tibor Laczi) — немецкий компьютерный предприниматель венгерского происхождения, который совершенно случайно увидел Кубик Рубика во время очередной деловой поездки в Венгрию. Тибор зашел выпить кофе и заметил головоломку в руках у официанта кафе. Увлекающийся математикой Лакзи пришёл в восхищение от игрушки и занялся ее продвижением вместе с Томом Кремером — успешным изобретателем игр и основателем компании Seven Towns Ltd.
Настоящее «кубическое» нашествие началось лишь в 1980, когда в результате совместных усилий Тома Кремера и Тибора Лакзи, лицензию на производство кубика-Рубика купила компания Ideal Toy Corporation (именно она дала головоломке имя Rubik’s Cube), которая разместила заказ на 1 000 000 шт. после чего начала рекламировать и продавать эту игрушку во всем мире. В то время было выпущено около 100 миллионов «легальных кубиков» и еще больше — подделок. В 80х через Кубик прошел, наверное, каждый десятый житель цивилизованного мира. На западе Кубик Рубика появился в мае 1980, а в СССР Кубик пришел «в массы» в 1981 году. По некоторым данным, права на выпуск игрушки обошлись СССР в немыслимую для советского человека сумму 3 миллиона долларов. Первыми силу головоломки ощутили на себе учителя — целые классы целеустремленно, не выходя на перемены, ожесточенно вертели Кубик. Школьники собирали его во время уроков под партами. Учителя, отобрав его во время уроков, сами скрипели кубиком на занятиях, отгородившись от учеников классным журналом. А потом допоздна засиживались в учительской, пытаясь собрать головоломку. В школах проходили «закрытые» чемпионаты на скорость — находись легендарные личности, которые смогли в первые годы «кубизации» собрать его за одну минуту (у самого Рубика в первый раз на сборку ушел целый месяц).
Счастливцев, обладающих настоящим Кубиком в начале 80х, было совсем не много, — кто-нибудь приносил Кубик в школу и к нему выстраивалась очередь потрогать головоломку, подержать в руках. Возможность осмысленно собрать его, при первом взгляде, казалась совершенно невероятной. Для тех, у кого кубика Рубика не было, в 1982 году журнал «Юный Техник» выпустил статью с иллюстрациями и чертежами под названием «Всем кубикам кубик» о том, как его сделать самостоятельно. Вскоре робкие критические заметки о мании «кубизма» по просьбе трудящихся сменились многочисленными публикациями «Что нужно сделать, чтобы все-таки собрать Кубик?» В те времена это смотрелось чрезвычайно интересно: в журнале «Наука и жизнь» рядом с рассказом о минеральных удобрениях и достижениях советской космонавтики большая статья — «Как собрать Кубик Рубика». Возможно, кто-то из читающих эти строки до сих пор помнит схему сборки по методу журнала “Наука и Жизнь”, состоящий из заклинаний вида Ф2В-1Л2.
Как писал в своей статье журнал «Огонек», Кубик Рубика открыл советскому народу проход в виртуальную реальность, хотя такого словосочетания в лексиконе советских людей тогда еще не было. А виртуальная реальность, как выясняется, очень даже была. Кубик оказался высококалорийным продуктом, одна игрушка с успехом заменяла: два съезда руководящей и направляющей, один чемпионат мира по хоккею с шайбой, двести пятьдесят граммов водки без закуски, месячную норму обезжиренного кефира и половину новогоднего застолья. В рейтинге подарков кубик намного превосходил как книгу, традиционно и лучший подарок, и источник знаний, так и почти самый лучший дар тех времен, флакон 0,75 восхитительной водки по прозвищу «Сибирская», а некоторым гражданам даже заменил секс, так как предполагал аналогичную трудоемкость, игривость мысли и занятость рук. Кубик крутили самозабвенно, отрешенно, прямо в метро, в трамвае, в конструкторских бюро, в санаториях, домах отдыха, в постели. А сколько человек ушли в запой, так и не сумев справиться с изобретением коварного венгра? Кубики часто гибли — со злости отчаявшиеся сборщики швыряли их об стенку, давили ногами. В нормальной (в смысле интеллигентной) семье тогда полагалось иметь не меньше двух кубиков одновременно — чтобы никому не приходилось ждать, с завистью глядя на собирающего. Кубик стал лучшим подарком, который можно было дарить во всех случаях жизни: на день рождения, свадьбу, новоселье, Новый Год.
Ходят слухи, что знаменитые британские ученые — на этот раз психологи — дали головоломку человекообразным обезьянам. Шимпанзе вначале с чрезвычайным интересом отнеслись к ней, но затем стали беспокоиться, беспокойство перешло в сильное волнение, сравнимое с отчаянием. Одна из обезьян выбросила кубик подальше от клетки, другая пыталась его съесть, третья в злобе разломала на мелкие кусочки. Если бы только обезьяны!.. По наблюдениям этих научных деятелей и их коллег-невропатологов, некоторые люди, более часа безрезультатно вертевшие в руках игрушку, начинали нервничать, злиться, люди, излишне неуравновешенные, становились агрессивными, у них появлялось желание сломать кубик. Точно не известно, но вроде бы, к услугам таких экспансивных людей в продажу были выпущены небольшие пластмассовые топорики, предназначенные для «наказания» строптивой игрушки. К покупке прилагалась инструкция, в которой говорилось о том, что можно сделать из деталей разломанного кубика.
В 1982 году в Будапеште прошел чемпионат мира по собиранию Кубика Рубика. В нём приняли участие представители 19 стран — победители в национальных чемпионатах. Для решения предлагались три задания. Засчитывалось лучшее время из трёх попыток. Каждый участник состязания получал новый кубик фирмы «Политойс». Все кубики были одинаково сложно запутаны 25-30 вращениями с помощью ЭВМ. Компьютер программировался как генератор случайных чисел и неизвестным заранее образом определял поворачиваемую грань кубика, направление и угол поворота. До начала отсчёта времени каждому участнику соревнования давалось 15 секунд для изучения исходной раскраски кубика и выбора пути решения. От участников соревнования требовалось собрать кубик не более чем за 60 секунд. Лучшее время сборки — 22,95 секунды показал 16-летний студент из Лос-Анджелеса Минх Тхай, а один из претендентов на победу в спешке сломал подряд два кубика и был дисквалифицирован. Хотя ходили легенды о неведомых вундеркиндах, собиравших кубик чуть ли не за 10 секунд. По иронии судьбы, первый мировой чемпионат совпал с пиком популярности Кубика. Вскоре волна всемирного ажиотажа начнёт спадать, а сотни миллионов кубиков попрячутся по пыльным углам. Но до этого еще несколько лет.
Рекорд собирания Кубика Рубика в минувшие годы неоднократно переходил из рук в руки и сегодня является практически недостижимым для обычного человека временем: менее 8 секунд (в среднем из 5 попыток!!!!). Текущий рекорд фиксируется на сайте WCA. Интересно, что многим куберам удается собрать кубик менее чем 30 поворотами граней (соревнование Rubik’s Cube: Fewest moves), однако математики убеждены, что настанет день, когда кубик сможет быть повержен не более чем 22 движениями из ЛЮБОГО изначального положения, а не только в случае редкой удачи!
Никаких проблем со сбытом головоломки не было, были проблемы с производством. Венгрия физически не могла делать больше нескольких миллионов штук в год. Фабрики по изготовлению кубиков открываются в Гонконге, Тайване, Коста-Рике и Бразилии.
Страсть к игрушке не имела языковых, социальных и возрастных границ. Почтенные матроны и менеджеры банков, игроки в бейсбол и пилоты, работники библиотек и дежурные на парковках вертели кубик круглые сутки. Во многих ресторанах кубик входил в число обязательных предметов сервировки стола наряду с солонкой и перечницей. От непрерывной многочасовой игры у людей попросту сводило запястья.
В авангарде всемирного движения шла молодежь, школьники и студенты. Сложность сборки кубика вызвала к жизни поток специальных изданий по проблеме: было выпущено более 60 книг. Не отставал и советский журнал «Наука и жизнь», на протяжении нескольких лет в каждом номере уделявший внимание кубику Рубика.
Уже в 1980-м кубик получает венгерский национальный приз за лучшее изобретение и выигрывает конкурсы на лучшую игрушку в США, Великобритании, Франции и Германии. В 1981 году кубик попадает в экспозицию Нью-Йоркского музея современного искусства (MOMA). В том же году ограниченным тиражом в Англии выходит
Royal Puzzle — версия Кубика Рубика, посвященная свадьбе принца Чарльза и леди Дианы, состоявшейся 29 июля 1981.
Между тем, падение интереса к разноцветному искусителю вовсе не было дружным и повсеместным. Так могло показаться лишь производителям игрушки, на волне игорного помешательства наштамповавшим десятки миллионов «лишних» кубиков и на год-другой забывшим, что рынок сбыта всё же ограничен. А может быть, тому виной вся масса неумех, так и не сумевших собрать Кубик? Или же логику пространственных поворотов заслонили политические дебаты, партии и демонстрации? Или просто настала электронная эра, и народ ушел играть в «Тетрис»?
В любом случае, результатом стал коллапс в сфере продаж, огромные складские запасы нереализованных кубиков на фабриках и в магазинах, а также отсутствие новых заказов на производство. Поэтому, начиная с 1983 года, кубик стало всё труднее, и затем и вовсе невозможно найти на прилавке.
Однако человек, стоявший у истоков экономического чуда Кубика Рубика, Том Кремер, сохранил светлую веру в непреходящий потенциал головоломки. Кремер считал его, подобно «Монополии» или Scrabble, игрой на все времена. Воспользовавшись удобной ситуацией, в 1985 году английская фирма Seven Towns принадлежащая Кремеру перекупает права на кубик и к 1991 году очень осторожно и выборочно начинает вновь потихоньку выпускать его на рынок. Победное возвращение “игрушки №1” началось в 1996 г., когда усилиями все того же Тома Кремера в США было продано 300 тыс. кубиков, а в Великобритании годом позже — 100 тыс.
На фото: Том Кремер и Эрно Рубик, 2007г
С появлением персональных компьютеров появился и виртуальный кубик Рубика — программы, в которых можно собирать головоломку на экране компьютера или смартфона. Однако, живой, осязаемый, фирменно скрипящий кубик Рубика, стал от этого только еще более популярным! Возможно по-этому, несмотря на то, что молодое поколение отдает предпочтение электронным играм, кубика Рубика регулярно объявляют бестселлером различные исследования, рейтинги и отраслевые издания.
В 2013г Rubik’s представил обновленный кубик Рубика, революционным отличием которого стало отсутствие наклеек — они были заменены на более практичные и красивые пластиковые вставки. Вместе с этим был обновлен и механизм головоломки (впервые за многие десятки лет!!), который получил шарообразное ядро, специальные тип пластика, обеспечивающий более плавное скольжение и мягкие повороты.
Что касается изобретателя, то он в неполные 40 лет став миллионером, богатейшим частным лицом Венгрии и человеком-легендой, объездив весь мир, достаточно быстро устал от публичного внимания и ушел в тень, чтобы спокойно заниматься своими экспериментами и изобретениями в основанной им Rubik’s Studio. Появившаяся таким образом знаменитая Змейка Рубика — развитие древнекитайской геометрической головоломки «танграм», также имела оглушительный успех, но до популярности незабвенного кубика даже ей более чем далеко.
Сейчас Энре Рубик проживает в пригороде Будапешта, изредка выступая с многозначительными и квазирелигиозными заявлениями для прессы, одно из которых приведено курсивом в начале страницы сразу под фотографией автора. Ежегодно многие любители и коллекционеры головоломок отмечают день рождение Рубика — 13 июля 1944г.
В 1988 г Эрно Рубик основал Международный фонд Рубика с целью поддержки молодых изобретателей. С 1990 г. Рубик — председатель венгерской инженерной академии, с 1996 г. – ее почетный председатель. В 1983 г. был награжден Венгерской Государственной премией, а в 1995 – премией им. Денеша Габора за творчество и инновативную деятельность. Сейчас Рубик заинтересовался компьютерами и ищет возможности, которые смогут изменить взаимоотношения компьютера и пользователя.
Количество комбинаций кубика Рубика (математика).
| Количество перестановок для кубика Рубика 2х2х2 | |
| Количество перестановок для кубика Рубика 3х3х3 | |
| Количество перестановок для кубика Рубика 4х4х4 | |
| Количество перестановок для кубика Рубика 5х5х5 |
Кубик Рубика: только факты
43,252,003,274,489,856,000 возможных комбинаций, и только 1 правильное решение.
Более 350 миллионов кубиков Рубика продано во всем мире. Если сложить их в 1 ряд, то полосу из кубиков Рубика можно было бы выложить с Северного Полюса до Южного Полюса.
Изобретен профессором архитектуры и дизайна Эрно Рубиком в 1974 в Будапеште как учебное пособие по геометрии, и не экспортировался из Венгрии до 1980г.
Первоначальное название, данное изобретателем — «Магический Кубик». Головоломка была переименована в кубик Рубика после презентации на старейшей выставке игрушек в Нюрнберге в 1980г и последующим миллионным заказом для США.
На пике популярности в 1980г, головоломку крутил каждый пятый житель земли!
Размер стороны оригинального кубика Рубика — 57мм. Это «золотой стандарт» игрушки, вычисленный Эрно Рубиком и до сих пор соблюдаемый брендом Rubik’s.
- Сотни тысяч видео-роликов о головоломке на YouTube
Первый Чемпионат Мира по кубику Рубика пошел в Венгрии в 1982г и был выигран студентом из Лос-Анджелеса по имени Мин Тай (Minh Thai), собравшим кубик Рубика за 22,95сек. Соревнования проходят в нескольких номинациях: сборка одной рукой, ногами, с закрытыми глазами и даже под водой на одном дыхании.
Считается, что дольше всех собирал свой кубик Рубика британец Грэм Паркер, получивший его в подарок на свое 19-летие и наконец собравший его впервые совсем недавно, в 47-летнем возрасте, т.е. через 26 лет!
Какой кубик выбрать для сборки одной рукой?
OH (One-Handed) — популярная спидкуберская дисциплина, в которой для сборки кубика Рубика используется только одна рука. В ней есть своя специфика — особые методики, адаптированные алгоритмы, а также необходимость подходящего для этой дисциплины кубика. Далеко не всегда те модели, которые Вас устраивали в классической сборке, подойдут для одной руки.

На удобство влияют 3 основных фактора:
- Качество кубика. Как бы банально и абстрактно это ни звучало, но если модель плоха даже для сборки двумя руками, стоит ли ожидать от нее чего-то большего в OH?
- Размер кубика. Поскольку во время сборки нужно довольно сильно тянуться пальцами, манипулируя гранями, трёшки с габаритами 56-57 мм часто оказываются неудобными. Они занимают много места в руке, препятствуют быстрым перехватам и чистому исполнению алгоритмов.
- Наличие магнитов. Этот пункт довольно спорный: одни считают, что преодоление силы магнитов способствует большему утомлению пальцев, а другие уверены в улучшении результатов, благодаря повышенному контролю и стабилизации, а также «помощи» в доведении граней. Администрация Кубмаркет больше склоняется ко второму мнению.
Для начала рассмотрим подробнее второй пункт, обозначив некоторые модели компактного размера, подходящие для сборки одной рукой.
1) GAN 354 M
Для многих этот куб является золотым стандартом в OH, а иной раз и в сборке двумя руками. Компактный размер 54мм оптимален для вращения кубика одной рукой, причем у других фирм данный размер не встречается — как правило, кубы делают меньше или больше. Ган 354 невероятно технологичный и качественный, большинство покупателей остается довольными кубиком, хотя, конечно, находятся и те, кто предпочитает что-то другое. GAN 354 M довольно дорогой, однако его цена сполна оправдана результатом.
2) MoFangGe 3×3 Valk 3 mini 47.4 mm
Этот кубик Рубика является уменьшенной копией знаменитого Valk 3. Сложно сказать однозначно, являются ли его габариты удачными, ведь 47.4 мм — это чуть ли не на сантиметр меньше стандарта, что поначалу весьма непривычно. Такой странный выбор размера обусловлен тем, что выход кубика приурочен к мировому рекорду Матса Валка — 4.74 сек.
В любом случае, идентичная модель классического размера давно одобрена огромным количеством спидкуберов, так что и к мини-версии стоит присмотреться. Если нет возможности покрутить такой куб перед покупкой, то хорошенько подумайте, ведь взрослому спидкуберу с большими руками собирать на нем вряд ли будет удобно. Зато ребятам помладше и девочкам он может очень понравиться.
3) MoYu MoFangJiaoShi 3×3 mini 50 mm
Казалось бы, от бюджетного кубика много ожидать не стоит, однако данная модель действительно хороша. Во-первых, она сделана весьма качественно, так что отлично подходит и для сборки двумя руками, незначительно уступая более дорогим моделям. Во-вторых, размер 50 мм покажется удобным для многих в сборке одной рукой. Да, это совсем немного больше предыдущего кубика, но эти габариты уже не кажутся такими миниатюрными. В любом случае, к кубику нужно будет привыкнуть, а перейти обратно на стандартные трешки в OH затем также получится не сразу, однако MF mini наверняка поможет Вам добиться хороших результатов в дисциплине.
Перечисленные модели, на наш взгляд, наиболее оптимальны среди мини-кубов, однако вы можете присмотреться и к другим кубикам от MoYu, Cyclone Boys и DaYan.
Важно помнить, что модели стандартного размера зачастую вполне могут устроить Вас для сборки одной рукой. Важно помнить, что тот самый «стандарт» за несколько лет успел поменяться. Раньше это был размер 57 мм, но теперь в это понятие вписываются размеры 55 мм, 55.5 мм и 56 мм. Если Вы видите трешку такого размера, и при этом она имеет хорошую репутацию, положительные отзывы и видеообзоры, то скорее всего для OH она тоже подойдет.
Оцените статью:
Спасибо за оценку20 интересных фактов о кубике Рубика :: Инфониак
 Невероятные факты
Невероятные факты Накануне 19 мая известной головоломке «кубик Рубика» исполнилось 40 лет. В 1974 году молодой преподаватель архитектуры Эрне Рубик из Будапешта создал практически невозможный объект.
Первый «Магический кубик», как его тогда называли, был продан в игрушечном магазине Будапешта в 1975 году.
Головоломка состояла из 26 уникальных миниатюрных кубиков. Это включает в себя и скрытые внутренние выступы, которые сцепляются с другими кубиками, в то же время, позволяя им вращаться.
Магический кубик был переименован кубиком Рубика в 1980-м году в честь его изобретателя.
Игра кубик Рубика
1. Рубик хотел создать рабочую модель для объяснения трехмерной геометрии.
2. Ему потребовалось больше месяца, чтобы узнать решение своей головоломки. Твердый кубик Рубика вращался и поворачивался, но при этом не ломался и не распадался на части. Некоторые люди до сих пор пытаются понять, как это происходит.
3. Кубик Рубика был признан Игрушкой года в 1980 и 1981 годах.
4. Больше 350 миллионов кубиков Рубика было продано по всему миру, благодаря чему он стал самой продаваемой игрушкой всех времен.
5. У кубика Рубика 43 252 003 274 489 856 000 возможных конфигураций. С учетом 6 цветных сторон, 21 частей и 54 поверхности, существует более 43 квинтиллионов различных возможных конфигураций.
6. Если бы вы поворачивали кубик Рубика каждую секунду, вам бы потребовалось 1400 триллионов лет, чтобы пройти все конфигурации.
7. Если бы вы начали этот проект во время Большого взрыва, вы бы до сих пор не закончили.
Сборка кубика Рубика
8. Однако лучшие спидкуберы могут собрать кубик меньше, чем за 6 секунд. Спидкуберы — это люди, участвующие в спикубинге – виде спорта, в котором участники занимаются быстрой сборкой кубика Рубика.
9. Нынешний рекорд по спидкубингу принадлежит Мэтсу Волку (Mats Valk) из Нидерландов. Он решил головоломку за 5,55 секунд.
10. Он побил рекорд австралийца Феликса Земдегса (Feliks Zemdegs) который составил 5,66 секунд.
11. Некоторые спидкуберы больше заботятся о стиле исполнения, чем просто скорости.
12. Хотя этому конкурсанту потребовалось 25 секунд, чтобы собрать кубик Рубика, он делал это, одновременно отжимаясь одной рукой.
13. Другому участнику потребовалось 28,80 секунд, чтобы найти решение с завязанными глазами.
14. Трехлетний ребенок из Китая собрал кубик меньше, чем за 2 минуты.
15. Лего-робот, работающий на смартфоне, может собрать кубик Рубика быстрее человека. Робот, названный «CubeStormer 3» решил головоломку за 3,253 секунды.

16. Любая комбинация кубика Рубика решается за 20 или меньше движений.
Кубик Рубика: рекорды
17. Самый большой кубик Рубика размером 3 метра и весом 500 кг находится в городе Ноксвилл, в штате Теннесси США.
18. Самый маленький кубик Рубика шириной 10 мм был сделан российским программистом Евгением Григорьевым. Это полностью функциональный кубик, который можно собирать, как обычный кубик.
19. Самым дорогим кубиком стал «Кубик-шедевр» созданный Diamond Cutters International в 1995 году. Кубик был выполнен из 22,5 карат аметиста, 34 карата рубинов, 34 карата изумрудов и 18-каратного золота, и оценивался в 1,5 миллиона долларов.
20. «Если вы любопытны, вы найдёте головоломки вокруг вас. Если вы решительны, вы их решите», — говорил Эрне Рубик.
Как собрать кубик Рубика (видео)
Математика кубика Рубика — Википедия
Эта статья о математических методах, использовавшихся для анализа кубика Рубика; о сборке кубика Рубика вручную см. b:Сборка кубика Рубика. Запутанный кубик Рубика Собранный кубик Рубика
Собранный кубик РубикаМатема́тика ку́бика Ру́бика — совокупность математических методов для изучения свойств кубика Рубика с абстрактно-математической точки зрения. Эта математика изучает алгоритмы сборки кубика и оценивает их. Основана на теории графов, теории групп, теории вычислимости и комбинаторике.
Существует множество алгоритмов, предназначенных для перевода кубика Рубика из произвольной конфигурации в конечную конфигурацию (собранный куб). В 2010 г. строго доказано, что для перевода кубика Рубика из произвольной конфигурации в собранную конфигурацию (часто этот процесс называют «сборкой» или «решением») достаточно не более чем 20 поворотов граней[1]. Это число — диаметр графа Кэли группы кубика Рубика[2]. В 2014 г. доказано, что для решения кубика Рубика только с помощью поворотов граней на 90° всегда достаточно 26 ходов[3].
Алгоритм, который решает головоломку за минимально возможное количество ходов, называют алгоритмом Бога>>>.
В этой статье для обозначения последовательности поворотов граней кубика Рубика 3×3×3 используются «обозначения Сингмастера»[4][5], разработанные Дэвидом Сингмастером и опубликованные им в 1981 году.
Буквы L,R,F,B,U,D{\displaystyle L,R,F,B,U,D} обозначают поворот на 90° по часовой стрелке левой (left), правой (right), передней (front), задней (back), верхней (up) и нижней (down) граней соответственно. Повороты на 180° обозначаются добавлением справа к букве цифры 2 или добавлением в верхнем индексе цифры 2 справа от буквы. Поворот на 90° против часовой стрелки обозначается добавлением штриха ( ′ ) или добавлением в верхнем индексе -1 справа от буквы. Так, например, записи L2{\displaystyle L^{2}} и L2{\displaystyle L2} эквивалентны, так же как записи L′{\displaystyle L’} и L−1{\displaystyle L^{-1}}.
Существует два наиболее распространённых способа измерения длины решения (метрики). Первый способ — одним ходом решения считается поворот грани на 90° (quarter turn metric, QTM). По второму способу, за 1 ход также считается и полуоборот грани (face turn metric, FTM, иногда это обозначают HTM — half-turn metric). Так, F2 (поворот передней грани на 180°) должен считаться за два хода в метрике QTM или за 1 ход в метрике FTM[6][7].
Для указания в тексте длины последовательности для используемой метрики используется нотация[8][9][10], состоящая из цифр числа ходов и строчной первой буквы обозначения метрики. 14f обозначает «14 ходов в метрике FTM», а 10q — «10 ходов в метрике QTM». Чтобы указать, что количество ходов является минимальным в данной метрике, используется звёздочка: 10f* обозначает оптимальность решения в 10 ходов FTM.
Кубик-Рубика может рассматриваться как пример математической группы.
Каждый из шести поворотов граней кубика Рубика может рассматриваться как элемент симметрической группы множества 48 этикеток кубика Рубика, не являющихся центрами граней. Более конкретно, можно пометить все 48 этикеток числами от 1 до 48 и сопоставить каждому из ходов {F,B,U,D,L,R}{\displaystyle \{F,B,U,D,L,R\}} элемент симметрической группы S48{\displaystyle S_{48}}.
Тогда группа кубика Рубика G{\displaystyle G} определяется как подгруппа S48{\displaystyle S_{48}}, порождаемая шестью поворотами граней:
G=⟨F,B,U,D,L,R⟩{\displaystyle G=\langle F,B,U,D,L,R\rangle }Порядок группы G{\displaystyle G} равен [11][12]:
|G|=8!⋅12!⋅38⋅2123⋅2⋅2=43 252 003 274 489 856 000=227⋅314⋅53⋅72⋅11{\displaystyle |G|={\dfrac {8!\cdot 12!\cdot 3^{8}\cdot 2^{12}}{3\cdot 2\cdot 2}}=43\ 252\ 003\ 274\ 489\ 856\ 000=2^{27}\cdot 3^{14}\cdot 5^{3}\cdot 7^{2}\cdot 11}Каждая из 4,325⋅1019{\displaystyle 4{,}325\cdot 10^{19}} конфигураций может быть решена не более чем за 20 ходов (если считать за ход любой поворот грани)[1].
Наибольший порядок элемента в G{\displaystyle G} равен 1260. Например, последовательность ходов (R U2 D′ B D′){\displaystyle (R\ U^{2}\ D^{\prime }\ B\ D^{\prime })} необходимо повторить 1260 раз, прежде чем кубик Рубика вернётся в исходное состояние[13].
Алгоритм Бога начали искать не позже 1980 года, когда открылся список рассылки для любителей кубика-Рубика[6]. С тех пор математики, программисты и любители стремились найти алгоритм Бога, чтобы на практике за минимальное число ходов собирать кубик-Рубика. Так как нужно кубик собрать полностью, то в алгоритме требовалось число ходов, достаточное для сборки головоломки.
В 2010 году программист из Пало-Альто Томас Рокики, учитель математики из Дармштадта Герберт Коцемба, математик из Кентского университета Морли Дэвидсон и инженер компании Google Inc. Джон Детридж доказали, что кубик-Рубика из любого разобранного состояния можно собрать за 20 ходов. При этом любой поворот грани считался одним ходом. Объём вычислений составил 35 лет процессорного времени, пожертвованного компанией Google[1][14][15]. Технические данные о производительности и количестве компьютеров не разглашаются. Продолжительность вычислений составляла несколько недель[16][17][18].
В 2014 году Томас Рокики и Морли Дэвидсон доказали, что кубик-Рубика можно собрать не более чем в 26 ходов без использования поворотов на 180°. Объём вычислений составил 29 лет процессорного времени в суперкомпьютерном центре Огайо[3].
Нижние оценки числа Бога[править | править код]
Легко показать, что существуют разрешимые конфигурации[19], которые не могут быть решены менее чем в 17 ходов в метрике FTM или 19 ходов в метрике QTM.
Эту оценку можно улучшить, принимая во внимание дополнительные тождества: коммутативность поворотов двух противоположных граней (L R = R L, L2 R = R L2 и т. д.) Подобный подход позволяет получить нижнюю оценку для числа Бога в 18f или 21q[20][21].
 «Суперфлип» — первая обнаруженная конфигурация, находящаяся на расстоянии 20f* от начальной
«Суперфлип» — первая обнаруженная конфигурация, находящаяся на расстоянии 20f* от начальнойЭта оценка долго оставалась наилучшей известной. Она вытекает из неконструктивного доказательства, так как оно не указывает конкретный пример конфигурации, требующей для сборки 18f или 21q.
Одной из конфигураций, для которой не удавалось найти короткое решение, был так называемый «суперфлип» или «12-флип». В «Суперфлипе» все угловые и рёберные кубики находятся на своих местах, но каждый рёберный кубик ориентирован противоположно[22]. Вершина, отвечающая суперфлипу в графе кубика-Рубика, — локальный максимум: любой ход из этой конфигурации уменьшает расстояние до начальной конфигурации. Это позволило предположить, что суперфлип находится на максимальном расстоянии от начальной конфигурации. То есть суперфлип — это глобальный максимум[23][24][25].
В 1992 году Дик Т. Винтер нашёл решение суперфлипа в 20f[26]. В 1995 году Майкл Рид доказал оптимальность этого решения[27], в результате чего нижняя оценка числа Бога стала равной 20 FTM. В 1995 году Майкл Рид обнаружил решение «суперфлипа» в 24q[28]. Оптимальность этого решения доказал Джерри Брайан[29]. В 1998 году Майкл Рид нашёл конфигурацию, оптимальное решение которой составляло 26q*[30].
Верхние оценки числа Бога[править | править код]
Чтобы получить оценку сверху для числа Бога, достаточно указать любой алгоритм сборки головоломки, состоящий из конечного числа ходов.
Первые оценки сверху для числа Бога были основаны на «человеческих» алгоритмах, состоящих из нескольких этапов. Сложение оценок сверху для каждого из этапов позволяло получить итоговую оценку порядка нескольких десятков или сотен ходов.
Вероятно, первую конкретную оценку сверху дал Дэвид Сингмастер в 1979 году. Его алгоритм сборки позволял собирать головоломку не более чем за 277 ходов[16][31]. Позднее Сингмастер сообщил, что Элвин Берлекэмп[en], Джон Конвей и Ричард Гай разработали алгоритм сборки, требующий не более 160 ходов. Вскоре группа «Conway’s Cambridge Cubists», составлявшая список комбинаций для одной грани, нашла 94-ходовый алгоритм[16][32]. В 1982 году в журнале «Квант» был опубликован список комбинаций, позволяющих решить кубик Рубика в 79 ходов[33].
Алгоритм Тистлетуэйта[править | править код]
В начале 1980-х английский математик Морвин Тистлетуэйт разработал алгоритм, позволивший значительно улучшить верхнюю оценку. Детали алгоритма опубликовал Дуглас Хофштадтер в 1981 году в журнале Scientific American. Алгоритм был основан на теории групп и включал в себя четыре этапа.
Описание[править | править код]
Тистлетуэйт использовал ряд подгрупп длины 4
G=G0⊇G1⊇G2⊇G3⊇G4={1}{\displaystyle G=G_{0}\supseteq G_{1}\supseteq G_{2}\supseteq G_{3}\supseteq G_{4}=\{1\}}, где:- G0=⟨L,R,F,B,U,D⟩{\displaystyle G_{0}=\langle L,R,F,B,U,D\rangle }
- Эта группа совпадает с группой кубика Рубика G{\displaystyle G}. Её порядок равен[34][35]
- G1=⟨L2,R2,F,B,U,D⟩{\displaystyle G_{1}=\langle L^{2},R^{2},F,B,U,D\rangle }
- Эта подгруппа включает в себя все конфигурации, которые могут быть решены без использования поворотов левой или правой граней на ±90°. Её порядок равен
- G2=⟨L2,R2,F2,B2,U,D⟩{\displaystyle G_{2}=\langle L^{2},R^{2},F^{2},B^{2},U,D\rangle }
- Эта подгруппа включает в себя все конфигурации, которые могут быть решены при условии, что повороты четырёх вертикальных граней на ±90° запрещены. Её порядок равен
- G3=⟨L2,R2,F2,B2,U2,D2⟩{\displaystyle G_{3}=\langle L^{2},R^{2},F^{2},B^{2},U^{2},D^{2}\rangle }
- Эта подгруппа включает в себя все конфигурации, которые могут быть решены с использованием только поворотов на 180° (half-turns). Она получила название «группа квадратов» (squares group). Её порядок равен
- G4={1}{\displaystyle G_{4}=\{1\}}
- Эта подгруппа включает в себя единственную начальную конфигурацию.
На первом этапе произвольно заданная конфигурация из группы G{\displaystyle G} приводится к конфигурации, лежащей в подгруппе G1{\displaystyle G_{1}}. Цель второго этапа состоит в том, чтобы привести кубик к конфигурации, находящейся в подгруппе G2{\displaystyle G_{2}}, не используя поворотов левой и правой граней на ±90°. На третьем этапе кубик Рубика приводится к конфигурации, принадлежащей группе G3{\displaystyle G_{3}}, при этом повороты вертикальных граней на ±90° запрещены. На заключительном, четвёртом этапе, кубик Рубика полностью собирается поворотами граней на 180°.
Индексы подгрупп [Gi:Gi+1]{\displaystyle [G_{i}:G_{i+1}]} при i=0,1,2,3{\displaystyle i=0,1,2,3} равны соответственно 2048, 1082565, 29400 и 663552.
Для каждого из четырёх семейств правых смежных классов Gi/Gi+1{\displaystyle G_{i}/G_{i+1}} строится таблица поиска Ti{\displaystyle T_{i}}, размер которой совпадает с индексом подгруппы Gi+1{\displaystyle G_{i+1}} в группе Gi{\displaystyle G_{i}}. Для каждого класса смежности по подгруппе Gi{\displaystyle G_{i}} таблица поиска Ti{\displaystyle T_{i}} содержит последовательность ходов, переводящую любую конфигурацию из этого класса смежности в конфигурацию, лежащую в самой подгруппе Gi{\displaystyle G_{i}}.
Чтобы уменьшить количество записей в таблицах поиска, Тистлетуэйт использовал упрощающие предварительные ходы. Первоначально он получил оценку в 85 ходов. В течение 1980 года эта оценка была снижена до 80 ходов, затем до 63 и 52[16][36]. Студенты Тистлетуэйта провели полный анализ каждого из этапов. Максимальные значения в таблицах равны 7, 10, 13 и 15 ходам FTM соответственно. Так как 7 + 10 + 13 + 15 = 45, кубик Рубика всегда может быть решён в 45 ходов FTM[25][37][38].
Граф Шрайера[править | править код]
Граф Шрайера[en] — граф S(G,X,H){\displaystyle S(G,X,H)}, ассоциированный с группой G{\displaystyle G}, порождающим множеством X={xi|i∈I}{\displaystyle X=\{x_{i}|i\in I\}} и подгруппой H⊆G{\displaystyle H\subseteq G}. Каждая вершина графа Шрайера является правым смежным классом Hg={hg|h∈H}{\displaystyle Hg=\{hg|h\in H\}} для некоторого g∈G{\displaystyle g\in G}. Рёбра графа Шрайера представляют собой пары (Hg,Hgxi){\displaystyle (Hg,Hgx_{i})}.
Каждый из четырёх этапов алгоритма Тистлетуэйта представляет собой обход в ширину графа Шрайера Si(Gi,Xi,Gi+1){\displaystyle S_{i}(G_{i},X_{i},G_{i+1})}, где Xi{\displaystyle X_{i}} — порождающее множество группы Gi{\displaystyle G_{i}}.
Таким образом, верхняя оценка в 45 ходов равна
- ∑i=03(ϵ(vi)){\displaystyle \sum _{i=0}^{3}(\epsilon (v_{i}))},
где
- ϵ(vi){\displaystyle \epsilon (v_{i})} — эксцентриситет вершины vi∈Si{\displaystyle v_{i}\in S_{i}}, соответствующей единичному смежному классу Gi+1{\displaystyle G_{i+1}}.
Понятие графа Шрайера было использовано в работах Раду[39], Канкла и Купермана[40].
Модификации алгоритма Тистлетуэйта[править | править код]
В декабре 1990 года Ханс Клоостерман использовал модифицированную версию метода Тистлетуэйта для доказательства достаточности 42 ходов[1][20][41].
В мае 1992 года Майкл Рид показал достаточность 39f или 56q[42]. В его модификации использовалась следующая цепочка подгрупп:
- G0=⟨U,F,R,L,B,D⟩{\displaystyle G_{0}=\langle U,F,R,L,B,D\rangle }
- G1=⟨U,R,F⟩{\displaystyle G_{1}=\langle U,R,F\rangle }
- G2=⟨U,R2,F2⟩{\displaystyle G_{2}=\langle U,R^{2},F^{2}\rangle }
- G3={1}{\displaystyle G_{3}=\{1\}}
Уже через несколько дней Дик Т. Винтер снизил оценку в метрике FTM до 37 ходов[43].
В декабре 2002 года Райан Хайз разработал вариант алгоритма Тистлетуэйта, предназначенный для скоростной сборки кубика Рубика[44].
Двухфазный алгоритм Коцембы[править | править код]
 Промежуточное состояние кубика Рубика в алгоритме Коцембы. Ходы, разрешённые на втором этапе, сохраняют расположение меток «+» и «—»
Промежуточное состояние кубика Рубика в алгоритме Коцембы. Ходы, разрешённые на втором этапе, сохраняют расположение меток «+» и «—»Алгоритм Тистлетуэйта в 1992 году улучшил учитель математики из Дармштадта Герберт Коцемба.
Описание[править | править код]
Коцемба сократил количество этапов алгоритма до двух[20][45][46]:
- G0=⟨U,D,L,R,F,B⟩{\displaystyle G_{0}=\langle U,D,L,R,F,B\rangle }
- G1=⟨U,D,L2,R2,F2,B2⟩{\displaystyle G_{1}=\langle U,D,L^{2},R^{2},F^{2},B^{2}\rangle }
- G2={1}{\displaystyle G_{2}=\{1\}}
Наглядное описание группы G1{\displaystyle G_{1}} можно получить, если произвести следующую разметку[20][47]:
- Все этикетки U и D пометить знаком «+».
- Этикетки F и B на рёберных элементах FR, FL, BL и BR пометить знаком «—».
- Все остальные этикетки оставить без меток.
Тогда все конфигурации группы G1{\displaystyle G_{1}} будут иметь одну и ту же разметку (совпадающую с разметкой на собранном кубике).
Решение состоит из двух этапов. На первом этапе заданная конфигурация x∈G0{\displaystyle x\in G_{0}} переводится последовательностью ходов s1{\displaystyle s_{1}} в некоторую конфигурацию x′∈G1{\displaystyle x^{\prime }\in G_{1}}. Иными словами, задача первого этапа — восстановить разметку, соответствующую начальной конфигурации, игнорируя цвета этикеток.
На втором этапе конфигурация x′∈G1{\displaystyle x^{\prime }\in G_{1}} переводится последовательностью ходов s2{\displaystyle s_{2}} в начальную конфигурацию. При этом повороты боковых граней на ±90° не используются, благодаря чему разметка автоматически сохраняется.
Склейка последовательностей ходов s1{\displaystyle s_{1}} и s2{\displaystyle s_{2}} является субоптимальным решением к исходной конфигурации[20][46][48].
Альтернативные субоптимальные решения[править | править код]
Алгоритм Коцембы не останавливается после обнаружения первого решения. Альтернативные оптимальные решения на первом этапе могут привести к более коротким решениям второго этапа, что сократит общую длину решения. Алгоритм продолжает искать также неоптимальные решения на первом этапе в порядке возрастания их длины[20][46][48].
Особенности реализации[править | править код]
Для поиска решений на каждом из двух этапов применяется алгоритм IDA* с эвристическими функциями, основанными на стоимостях решения соответствующих подзадач[48].
Задача первого этапа сводится к поиску пути в пространстве с тремя координатами из разметки с координатами (x1, y1, z1) в разметку (0, 0, 0)[49]:
- Ориентация x1 восьми угловых элементов (2187 значений)
- Ориентация y1 двенадцати рёберных элементов (2048 значений)
- Расстановка z1 четырёх рёберных элементов FR, FL, BL и BR (495 значений)
Рассмотрим три подзадачи поиска пути из разметки (x1, y1, z1) в разметки (x1’, y1’, 0), (x1’, 0, z1’), (0, y1’, z1’). Значение эвристической функции h1, используемой на первом этапе, равно максимальной из стоимостей решения этих подзадач. Стоимости решения подзадач предварительно вычисляются и хранятся в виде баз данных с шаблонами[50][51].
Задача второго этапа сводится к поиску пути в пространстве с тремя координатами из конфигурации (x2, y2, z2) в конфигурацию (0, 0, 0)[52]:
- Перестановка x2 восьми угловых элементов (40320 значений)
- Перестановка y2 восьми рёберных элементов верхней и нижней граней (40320 значений)
- Перестановка z2 четырёх рёберных элементов среднего слоя (24 значения)
Рассмотрим три подзадачи поиска пути из конфигурации (x2, y2, z2) в конфигурации (x2’,
Y-метод — действительно простой способ собрать кубик Рубика / Habr
Введение
В статье рассматривается «Y-метод» сборки кубика Рубика — его легко понять и запомнить. Он основан всего на одной последовательности, которая называется «Y-движение». Поняв этот алгоритм, вы навряд ли забудете как собрать кубик самостоятельно.
Если попытаться нагуглить инструкцию по сборке кубика Рубика, то найдётся много вариантов с описанием «простой сборки», в том числе на википедии. Которые, в целом, действительно достаточно простые к пониманию, но обладают существенным недостатком. Для того, чтобы собрать кубик, нужно знать порядка пяти или более нетривиальных последовательностей (алгоритмов) для перестановки отдельных кубиков, для сборки кубика Рубика по слоям. В связи с чем запомнить и воспроизвести самостоятельно эти инструкции затруднительно. Недавно я случайно наткнулся на упоминание алгоритма «The Ultimate Solution to Rubik’s Cube», о котором утверждалось, что его легко запомнить и понять, и в нём используются всего две последовательности. А когда стал выяснять подробнее, то нашёл также и другой алгоритм — «Y-метод», тоже простой и использующий всего одну последовательность.
К сожалению, описания данного алгоритма на русском я не нашёл, поэтому я решил восполнить этот пробел. Также мне кажется, что главное в этом методе — понимание того как он работает. Поэтому тут я не предлагаю готовых наборов движений для конкретных ситуаций, а вместо этого я постарался подробнее описать что происходит.
Картинки в данной статье сгенерированы с помощью инструмента на сайте ruwix.com. Ссылки на картинках откроют этот инструмент с параметрами, соответствующими картинке. Это либо описываемое состояние кубика и вы сможете его повертеть мышкой, или, в некоторых случаях, там заданы описываемые движения, которые можно «проиграть» туда-обратно.
Y-движение
Основу данного алгоритма составляет Y-движение. И довольно важная составляющая алгоритма — это разобраться в механике этого движения.
Данная последовательность поворотов так называется из-за того, что кубики, которые она затрагивает, выглядят как буква «Y», составленная тремя рёбрами, выходящими из одного угла кубика.
Y-движение довольно простое и состоит из четырёх поворотов двух смежных граней, например правой и передней. В распространённой нотаци поворотов для кубика Рубика это выглядит так: R’ F R F’. Что можно описать следующим образом:
- правая грань против часовой стрелки на четверть оборота
- передняя грань по часовой стрелке на четверть оборота
- правая грань по часовой стрелке на четверть оборота
- передняя грань против часовой стрелки на четверть оборота
То есть грани сначала по очереди поворачиваются «на себя», а потом в обратном порядке «от себя».
Назовём этот вариант «правым Y-движением» (т.к. поворачивается сначала грань справа). В этом случае меняется положение кубиков на ребре, общем у данных граней и на верхних рёбрах. Если начинать повороты с передней грани, то будут затронуты те же самые кубики, такой вариант мы будем называть «левым Y-движением» (т.к. поворачивается сначала грань слева).
Также можно начинать с поворотов «от себя» — это будет то же самое, если бы мы перевернули кубик и начинали с поворотов «на себя», поэтому назовём такие варианты «правым и левым перевёрнутым Y-движением». При перевёрнутых Y-движениях будет также затронуто смежное ребро, а также уже не верхние, а нижние рёбра, соседние с ним.
Принципиальной разницы во всех этих движениях, конечно же, нет. Такое разнообразие нужно исключительно для удобства.
Перечислим некоторые свойства Y-движений:
- Правое и левое Y-движения обратны друг другу, т.е. последовательность правого и левого или левого и правого движений не изменят состояния кубика.
- Одно Y-движение приводит к тому, что меняются местами в паре два угловых кубика на смежной грани и два других угловых кубика. А три кубика находящиеся посередине рёбер (рёберные) перемещаются по кругу.
- Как можно догадаться, после двух движений угловые кубики возвращаются на свои места. Но при этом они оказываются повёрнутыми.
- И если выполнить три раза по два движения, то кубики повернутся три раза и в результате вернутся в исходное состояние.
- Рёберные кубики возвращаются в исходное состояние после цикла из трёх движений.
- Таким образом, если выполнить Y-движение шесть раз подряд, то состояние кубика вернётся в изначальное.
- После одного Y-движения рёберные кубики перемещаются в направлении первого поворота, при этом два кубика как бы поворачиваются вдоль соответствующих граней (вокруг их оси), а третий также поворачивается, но при этом переворачивается. Переворачивается тот кубик, который перемещается между верхними рёбрами, в случае обычного (не перевёрнутого) Y-движения. При работе с рёберными кубиками Y-движение вдоль одних и тех же рёбер можно производить повернув кубик в разных направлениях, тем самым добиваясь переворота нужного нам кубика.
Последовательность сборки кубика
Сначала собираются два нижних слоя кубика за исключением одного вертикального ребра, проходящего через эти слои. Это место мы оставляем себе как пространство для манёвра. Нижний крест и нижние угловые кубики собираются довольно просто, но если есть затруднения, то не так сложно приспособить Y-движение для этого или посмотреть одну из инструкций для простой послойной сборки кубика.
Далее нужно собрать средние кубики на вертикальных рёбрах (рёберные). Для этого нужно повернуть верхнюю грань с нужным кубиком, чтобы он оказался на одной из соседних с целевым ребром граней. А также временно (не забываем потом вернуть на место) повернуть нижнюю грань, чтобы на месте целевого ребра оказался кубик, который мы специально оставили несобранным. Теперь можно воспользоваться Y-движением, чтобы переместить кубик с верхней грани на нужное нам место. Y-движение нужно делать такое, чтобы этот рёберный кубик повернулся в нужном направлении в сторону ребра и если нужно, то перевернулся.
Если нужный кубик не находится на верхней грани, то нужно его предварительно, также Y-движением, «освободить» оттуда, не забывая опять же подставить несобранный угол на нижней грани.
Пока что мы собрали два нижних слоя без одного ребра. Далее нам нужно будет собрать два рёберных кубика на верхних рёбрах, которые не граничат с тем, что мы специально не собираем. После этого из рёберных кубиков останется только три несобранных, на рёбрах, которые формируют букву «Y»: вертикальное, которое мы не собирали, и два верхних ребра, соседних с ним.
И, конечно же, мы собираем их с помощью одного или нескольких Y-движений, переворачивая и ставя на нужные места. Тут только нужно учесть один момент с количеством перестановок, который описан чуть ниже.
При сборке последних пяти рёберных кубиков нам может понадобиться развернуть эту букву «Y», чтобы сделать Y-движение в другом направлении (поворачивая другие грани вдоль этих рёбер), таким образом добиваясь перемещения нужных нам кубиков на другие места с переворотом или без него.
К этому моменту у нас будет почти собранный кубик, в котором не собраны только угловые кубики на верхней грани и на вертикальном ребре, которое мы не собирали. Описанными ниже методами сначала переставляем углы друг с другом, чтобы они оказались на своих местах, возможно неправильно ориентированные. А потом разворачиваем их.
Ура, наш кубик собран!
Считаем перестановки
На что же нужно обратить внимание когда мы собираем пять последних рёберных кубиков. Когда их останется только три, то чтобы у всё получилось с перестановкой их в пределах буквы «Y», нужно чтобы либо они все находились на своих местах (возможно перевёрнутые) или же все были не на своих местах. Это связано с тем, что Y-движение переставляет три рёберных кубика одновременно. Если рассмотреть это с точки зрения попарных обменов кубиков местами на соседних рёбрах, то происходит два обмена (перестановки). Теперь должно быть понятно почему в случае, когда у нас ровно два кубика не на своих местах, то мы не сможем их собрать. Т.к. нам нужно совершить одну перестановку, а с помощью Y-движений мы можем сделать только чётное число перестановок.
Что же делать в таком случае? Обратим внимание, что если повернуть грань кубика, то мы поменяем местами одновременно четыре рёберных кубика, что будет эквивалентно трём перестановкам, т.е. нечётному числу, что нам и нужно. Из этого следует, что верхняя грань должна быть правильно ориентирована для того, чтобы мы могли собрать последние три рёберных кубика. Если так вышло, что последние три рёберных кубика требуют одной перестановки, то это значит, что нужно переставить на соседние места два рёберных кубика, уже собранные на верхней грани.
Кроме того, мы можем заранее, до сборки первых двух кубиков из этой пятёрки, подсчитать число перестановок, которые потребуются, чтобы поставить все пять рёберных кубиков на свои места. Если это число чётное, то верхняя грань ориентирована правильно. А если нечётное, то её нужно повернуть один раз в любую сторону. Таким образом, мы сразу сможем поставить те два кубика на нужные места.
Работа с угловыми кубиками
На последнем этапе сборки нам нужно переставлять угловые кубики местами и поворачивать их. Для этого воспользуемся перечисленными ранее свойствами Y-движения в отношении угловых кубиков. Т.к. удобнее работать с угловыми кубиками, расположенными на верхней грани, то для этого нам больше подойдёт перевёрнутое Y-движение (начинается с поворота «от себя»). В этом разделе будет использоваться именно эти варианты, без дополнительного уточнения. Обратим сразу внимание, что это движение меняет состояние только одного кубика на верхней грани — это угловой кубик на «смежном ребре».
Для перестановки угловых кубиков заметим, что одиночное Y-движение (как левое, так и правое) меняет местами пару угловых кубиков на «смежном ребре», а также что последовательное применение левого и правого Y-движения (или правого и левого) возвращает весь кубик в исходное состояние. Давайте подумаем, что произойдёт, если между этими движениями мы повернём верхнюю грань. Как мы уже обратили внимание, на верхней грани меняется только один угловой кубик, который переставляется с парным кубиком на ребре. В таком случае у нас произойдёт два обмена угловыми кубиками на ребре, но каждый раз сверху будет подставлен разный угол, а все остальные кубики останутся как были (конечно, нужно ещё не забыть повернуть верхнюю грань в исходное состояние). Таким образом, мы осуществили обмен местами трёх угловых кубиков — одного с нижней грани и двух с верхней.
Теперь разберёмся с поворотом кубиков. Для этого воспользуемся похожим трюком. Будем делать два последовательных Y-движения в одном направлении. В результате этого угловые кубики остаются на месте, но меняют свою ориентацию. Тут нас интересуют два варианта комбинации движений: три двойных движения в одном направлении (левые или правые) или двойное движение в одном направлении и двойное движение в обратном направлении. В каждом из этих вариантов весь кубик возвращается в исходное состояние. И мы опять будем между двойными движениями подставлять очередной нужный нам угол на место верхнего угла «смежного ребра». Таким образом мы можем повернуть либо три угловых кубика на одной грани в одном направлении, либо два угловых кубика на одной грани в разных направлениях, не меняя состояния остальных кубиков. Обратим внимание, что после двойного движения верхний кубик смежного ребра поворачивается в том же направлении, в котором осуществляется первое Y-движение.
Заключение
Не знаю как будет в вашем случае, но для меня плюс данного алгоритма не только в том, что его легко запомнить и не нужно зубрить инструкцию по сборке. Но также и в том, что теперь, собирая кубик, я собираю его сам, понимая что происходит, вместо почти механического следования инструкции, а это намного приятнее. Чего и вам желаю!
▲Обзор кубиков Рубика. Как правильно выбрать кубик 3х3
Всем привет. Уже около года я занимают продажей популярных головоломок кубиков Рубика. За этот период времени я получил возможность протестировать не менее 20-ти различных кубиков Рубика. В основном это модели с розничной ценой до 10 у.е. (250 грн.). Сегодня я хотел бы рассказать, какие модели кубиков 3х3 являются самыми удачными по соотношению цены и качества, а также какой кубик Рубика подойдет именно вам.
Кстати, купить любой описанный кубик можно у меня в магазине «Cubes.in.ua» (доставка только по Украине) =).
А еще у нас можно купить хенд спиннеры и fidget кубики!
Обзор недорогих кубиков Рубика 3х3 до 4 у.е.
На самом деле найти удачный кубик Рубика в таком ценовом диапазоне достаточно сложно. Обычно за такую стоимость продаются либо не скоростные кубики, либо самые дешевые модели из скоростных. К скоростным кубикам можно отнести такие модели как:
- YONGJUN Guanlong
- Qiyi Qihang
- Shengshou Legend
- ShengShou Track
- ShengShou Wind
Конечно большинство данных моделей с трудом можно назвать скоростными. Но даже в этом ценовом диапазоне есть кубик, который без труда можно использовать для тренировок скоростной сборки.
Обзор кубика Shengshou Legend
Если оценивать из тех моделей, которые я держал в рука, Shengshou Legend это самая удачная модель кубика в своем ценовом диапазоне. Заказать данный кубик Рубика можно в моем магазине.
Материалы
Кубик выпускается из черного и белого пластика. Пластик в кубиках используатся совсем не толстый, но при этом качество деталей очень хорошее. Наклейки наклеены очень аккуратно и ровно, цвета наклеек очень яркие. Кубик без проблем настраивается при помощи болтов под крышечками центральных кубиков.
Скоростные характеристики
Нужно отметить, что Shengshou Legend однозначно владеет характеристиками кубиков Рубика совсем другого диапазона =). Плавность вращения сторон на 10 из 10. Срезка углов также более чем хорошая, углы в 35-45 градусов не проблема. Реберные кубики в этом модели содержат специальные углубления, для того, чтобы уменьшить трение с другими кубиками. Мало того, этот кубик сложно развалить. Даже с ослабленными болтами, Легенду сложно развалить на части (при скоростной сборке такое может случиться).
Видео обзор Shengshou Legend
Shengshou Legend. Видео 2
Qiyi Qihang
На втором месте из моделей до 4-х у.е. я бы разместил кубик Qiyi Qihang. Данный кубик также можно отнести к скоростным, но вот что касается качества сборки и пластика, то тут могут быть нюансы. Пластик в кубике также достаточно тонкий. Если заглянуть внутрь кубика, то можно увидеть что разработчики Qihang решили сэкономить и на механизме. Внутренние части кубиков сделаны максимально экономично, что не очень приятно. Несмотря на свои недостатки, за такие деньги эта модель является не очень плохой.
YONGJUN Guanlong
В сегменте дешевых кубиков есть также популярная модель YONGJUN Guanlong. На самом деле, я не пополняю запасы этих кубиков, потому что даже если приходят заказы на этот кубик, то я стараюсь человека переубедить купить более качественную модель. На самом деле этот кубик уже сложно назвать скоростным. Да, стороны крутяться плавно, но срезка углов, механизм и качество материалов увы на очень низком уровне. Конечно, если вы решили купить кубик Рубика в качестве недорогого подарка, то Guanlong однозначно будет значительно лучше базарных кубиков ценой до 2 у.е., но если вы уже умеете собирать кубик, например корявый базарный =), то лучше рассмотрите более дорогие модели для развития своих навыков и интереса.
Обзор недорогих кубиков Рубика 3х3 ценой 5-6 у.е.
Данный ценовой диапазон я считаю оптимальным для выбора кубика Рубика начинающему спидкуберу. В данном ценовом диапазоне огромное количество моделей с хорошими характеристиками, а цена на самом деле не сильно отличается от первой группы дешевых кубиков. Рассмотрим нескольку кубиков в данном ценовом диапазоне которые мне доводилось держать в руках. Купить одну из указанных моделей кубика 3х3 можно тут.
- YongJun Chilong
- Cyclone Boys XuanFeng
- «Cyclone Boys» FeiWu 3x3x3
- «Cyclone Boys» Jisuzhiyun jisu
- YONGJUN Yulong
- Yuxin Fire Kylin
- Shengshou Rainbow 3x3x3
- YongJun Sulong
Начнем с самых удачных моделей, по соотношению цены и качества. На самом деле в этой ценовой группе уже сложно выбрать одного лидера. Лучшими я бы назвал такие кубы: YongJun Chilong, Cyclone Boys XuanFeng, Cyclone Boys FeiWu, Cyclone Boys Jisuzhiyun jisu и YONGJUN Yulong. А вот номинацию лучшее соотношение цена качество я бы отдал кубику Cyclone Boys FeiWu, с него собственно и начнем.
Обзор кубика Cyclone Boys FeiWu
Цена этой модели в рознице обычно на уровне 5-6 долларов. Лично я использую именно этот кубик Рубика 3х3. Поскольку я не профессиональный спидкубер, этой модели мне с головой хватает для того, чтобы обучатся и иногда ставить новые рекорды. Пройдемся по основным параметрам кубика.
Материалы
Данная модель делается только без наклеек, из цветного пластика. Что касается пластика, то с ним нет никаких проблем, наоборот, именно качество материалов и сборки являются одним из значительных преимуществ данного кубика. Пластик гладкий (глянцевый) и достаточно толстый. При этом качество материалов хорошее не только с внешней стороны кубика, но и внутри.
Скоростные характеристики
Кубик Cyclone boys отлично срезает углы и очень легко крутится. Механизм у кубика уже заметно отличается от дешевых моделей до 4 у.е. Что хотелось бы отметить:
- центральный кубик содержит юбочку, которая выполняет скорее всего функцию дополнительной направляющей и не позволяет реберным кубикам легко вываливаться со своих мест,
- реберные кубики имеют сложное строение,
- жесткий пластик делает вращение кубика очень приятным, быстрым и контрольным.
В своем ценовом диапазоне данный кубик не имеет аналогов с подобными характеристиками.
Вот видео, на котором можно посмотреть на то как я без сложностей выполняю сборку.
На сегодня мой личный рекорд сборки данным кубиком составляет около 20 секунд. При сборке из 3 попыток думаю что результат будет в пределах 25-27 секунд. На самом деле собирать быстрее мне мешает не кубик, а то что я не знаю всех формул, ну и немного туплю =).
Сразу же отмечу что данный кубик имеет и старшего брата – Cyclone Boys Jisuzhiyun. Есть версия с наклейками из черного пластика и без наклеек. Версия без наклеек немного больше по размеру кубика FeiWu и имеет еще более быстрое строение. Разница в цене между этими моделями минимальная.
Обзор кубика YJ Yulong
Другой достойный кубик в данном ценовом диапазоне это YJ Yulong. Кубик Yulong можно смело отнести к недорогим кубика 3х3, его цена кубика может колебаться в пределах 5,5-7 у.е. Модель бывает в трех цветовых решениях: черный с наклейками, без наклеек, без наклеек с розовым цветом.
Материалы
Пластик в кубике YJ Yulong испльзуется значительно плотнее нежели в более деневых кубиках. Кроме того, даже заглядывая внутрь кубика можно заметить что все сделано очень качественно, без заусениц и брака. Болты для стяжки сторон также выглядят очень массивно. Центральные кубики открываются и закрываются без проблем, при этом не выпадают во время сборки. На модели к наклейками, сами наклейки могут быть наклеены не очень ровно.
Скоростная сборка
Специально для обзор собрал несколько раз кубик на скорость, для того, то бы отметить слабые и сильные мести.
Начнем с того, что шумность версии из черного пластика обусловлена тем, что этот пластик заметно жестче, я бы отметил этот как заметное преимущество.
Что касается характеристики кубика Yulong в общем:
- отлично режет углы в 45 градусов,
- кубик не блокируется во время сборки,
- в механизме используются специальные углубления (рельсы) для уменьшения трения.
В отличии от Cyclone boys, Yulong имеет недостатки:
- во время сборки угловые кубики часто разворачиваются по часовой или против часовой стрелки.
- кубик имеет не очень прочную структуру если ослабить болты (очень легко вынимаются реберные и угловые кубики).
А вот и мой видео обзор кубика Yulong
Обзор кубика YJ Chilong
Самый дорогой кубик из данной подборки. Кубик Chilong не делают без наклеек. Цена данного кубика обычно не менее 6 у.е. На самом деле кубик действительно стоит этих денег.
Материалы
Chilong это однозначно старший брат кубика Yulong. При этом разработчики совсем не много изменили в строении кубика, заглянув внутрь я так и не понял что было изменено (кроме расположения рельсов). Как и в случае с Юлонгом, Чилонг сделан из хорошего пластика, более того, мне показалось что пластик еще лучше чем в Юлонге (возможно показалось).
Сборка на скорость
Сложно выделить какие-то параметры кубика Чилонг, которые бы отличали его от младшего брата Юлонга:
- хорошо режет углы,
- плавно и быстро вращаются стороны,
- кубик не блокируется при сборке,
- проворачиваются уголки при сборке на скорость =(,
- при интенсивной сборке кубик может развалится в руках =(.
В принципе если привыкнуть к особенностям кубика, то можно без проблем ставить новые рекорды, и до 20 секунд. Для написания обзора я собрал кубик несколько раз (один раз повернулся уголок), в основном результат был в пределах 27 секунд. Если учесть что тренируюсь в последнее время я мало, то результат неплохой =).
Обзор недорогих кубиков Рубика 3х3 ценой 7-10 у.е.
Итак мы подобрались к кубикам полупрофессионального уровня. Даже несмотря на то что эти кубики не топовые, подобными моделями могут собирать и очень продвинутые спидкуберы, при этом даже пользоваться такими на соревнованиях. Итак, что же я держал в руках:
- Yuxin Qylin
- MoYu Weilong
- Fungfu Qinghong
- Qiyi Thunderclap
- Qiyi Thunderclap II
Какие модели я бы выделил из этого списка. Специально для обзора я еще раз попробовал собрать кубики на скорость, для того, чтобы взвесить все за и против.
Обзор кубика Yuxin Qilin
Очно неплохая модель по соотношению цены и качества от популярного китайского бренда Yuxin.
Материалы
Стоит Qilin всего 7-8 у.е., при этом как и все кубики из этой ценовой категории качество материалов очень хорошее. Кубик хорошо лежит в руке, имеет приятные цвета и огромные дыры возле центрального кубика. Пластик в кубике используется толстый цвета приятные. Центральный кубик имеет очень сильно сглаженные углы, кубик почти круглый.
Скоростные характеристики
Как всегда начнем с углов. Углы режет очень хорошо, при этом хорошо режутся углы не только 45 градусов, но и более, а если взять угол очень большой, то срезка идет в обратную сторону, залочить кубик таким способом почти не получается. Центральный кубик имеет юбку, она сдерживает ребра и кубик не разваливается по время сборки. Внутренние части механизма очень необычные и выглядят внушительно и сложно.
Если говорить про недостатки, то стоит отметить, что угловые кубики при сборке легко проворачиваются. Других значимых недостатков не замечено. Модель действительно очень хороша по соотношению цены и качества.
Видео обзор Yuxin Qilin
Обзор кубика MoYu Weilong
Цена данного кубика на уровне 9-10 у.е. По идее это уже следующее звено цепочки кубиков Yulong -> Chilong -> Weilong.
Материалы
Все конечно на высоте. К пластику претензий нет, наклейки наклеены ровно, цвета наклеек стандартные для бренда JongJun (MoYu). Пластик плотный и без заметных дефектов.
Скоростные характеристики
Ну а теперь рассмотрим что же этот кубик демонстрирует при сборке на скорость. Углы режет хорошо, стандартный тест на срезку проходит отлично, но во время сборки иногда срезка проходит не очень приятно и быстро. В отличии от Yuxin Qilin, угловые кубики более устойчиво сидят на местах и не так часто проворачиваются при сборке на скорость. Центральный кубик содержит юбку, на самом деле это обязательный элемент для всех хороших кубов, ведь юбка помогает держать куби в сборе, а не разваливаться при сборке. Внутренний механизм далеко ушел от более дешевых Юлогна и Чилонга, реберные кубики и угловые имеют сложную конструкцию, которая делает кубик действительно скоростным. Неплохой кубик за свои деньги, но есть и более дешевые аналоги.
Видео обзор кубика MoYu Weilong
Обязательно посетите небольшой блог, в котором я собираю полезную информацию по сборке головоломок — http://magic-cubes.blogspot.com/.
Оцени пост!
Loading…Статьи по теме
- 21/12/2013 Внутренняя и внешняя переоптимизация сайта Каждый оптимизатор желает продвинуть свой сайт в ТОП 10 как можно быстрее и как можно дешевле. Это связано с […] Posted in Продвижение сайтов, Оптимизация сайта
- 13/01/2014 Свежие приобретения в Китае Я отношусь к тем людям, которые любят не только работать, но и активно отдыхать. После достаточно […] Posted in Хобби
- 08/10/2016 Обновления алгоритмов (фильтров) Google по датам. Penguin, Panda, Pigeon, Hummingbird В связи с постоянными изменениями алгоритмов Google нужно всегда держать руку на пульсе, а точнее следить […] Posted in Новости, Продвижение сайтов, Оптимизация сайта, Веб-аналитика













