Создано сфер в Destiny 2: что это такое
Сферы света – это тип предмета, с которым вы столкнетесь в «Destiny 2». Если вы вернулись из оригинальной игры «Destiny», вы уже знакомы с этими сферами и их действиями. Для новичков, однако, эти шары могут казаться случайными выпадающими предметами, которые не служат никакой цели, если вы не обращаете на них внимания.
Эти шары света на самом деле очень полезны, и они не так случайны, как вы думаете. Данная игровая механика была придумана в игре, чтобы побуждать игроков играть в команде и поощрять их за совместную работу. К ней можно относится по-разному, но играть становится куда легче, если вы все же выбиваете эти шары или собираете их. Существует определенный способ создания шаров, если вы не хотите проходить рейды легче.
Вы можете создавать их в «Destiny 2» всякий раз, когда убиваете врага своей суперспособностью, ультой.
Генерирование световых кругов или сбор их – это быстрый способ заполнить свой индикатор особых способностей или помочь вашим товарищам по команде заполнить их. Любой игрок в вашей собственной команде может подобрать эти шары, как только они выпадут из мертвых противников, так что, это дает некоторый дополнительный стимул для игроков, часто использовать свою суперспособность, когда они вместе в группе.

Чтобы получить максимальную отдачу от своей ульты, вам нужно подождать подходящего момента, чтобы получить как можно больше шаров света. Чем больше врагов вокруг вас, когда вы получаете суперспособность, тем больше сфер света вы будете генерировать в процессе их убийства.
Будет куда выгоднее, если вы будете чаще использовать ульту, создавая шары света, так как эти способности помогут вам быстрее восполнить полоску суперспособности. Существуют также различные типы снаряжения, которые делают эти сферы еще более полезными. Например, некоторые будут восстанавливать здоровье игрока при сборе этих сфер.

Также имейте в виду, что тип врага, которого вы победите, будет определять, сколько сфер создаете вы или ваши союзники. Если убить обычного, то обычно генерируется только один шар, а при победе над кем-то крупным обычно генерируется около четырех шаров.
list-name.ru
Сфера, шар, сегмент и сектор. Формулы и свойства
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
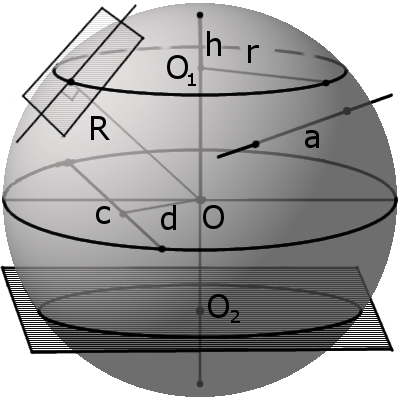
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x(x — x0)2 + (y — y0)2 + (z — z0)2 = R2
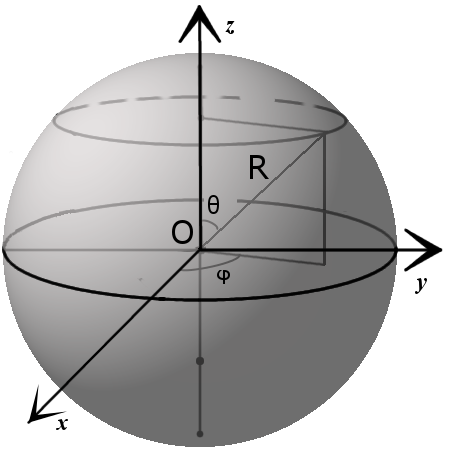 3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0): x = x0 + R · sin θ · cos φy = y0 + R · sin θ · sin φz = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле: r = √R2 — m2, где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
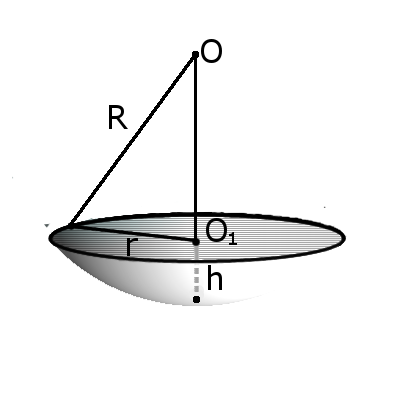 Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
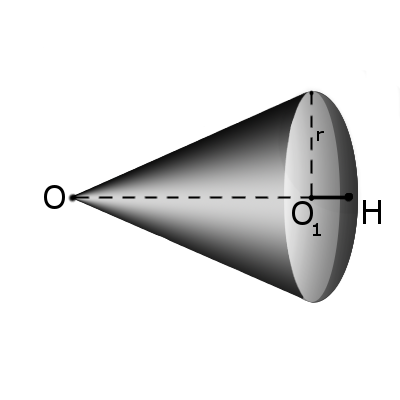 Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R): S = πR(2h + √2hR — h2) Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R): S = πR(2h + √2hR — h2) Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
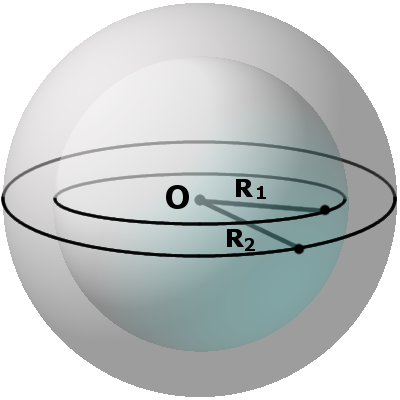 Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
ru.onlinemschool.com
формула, свойства, площадь поверхности нашей планеты
Сфера — это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.
Сфера: понятие в геометрии
Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние — это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).
На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка — центр сферы.
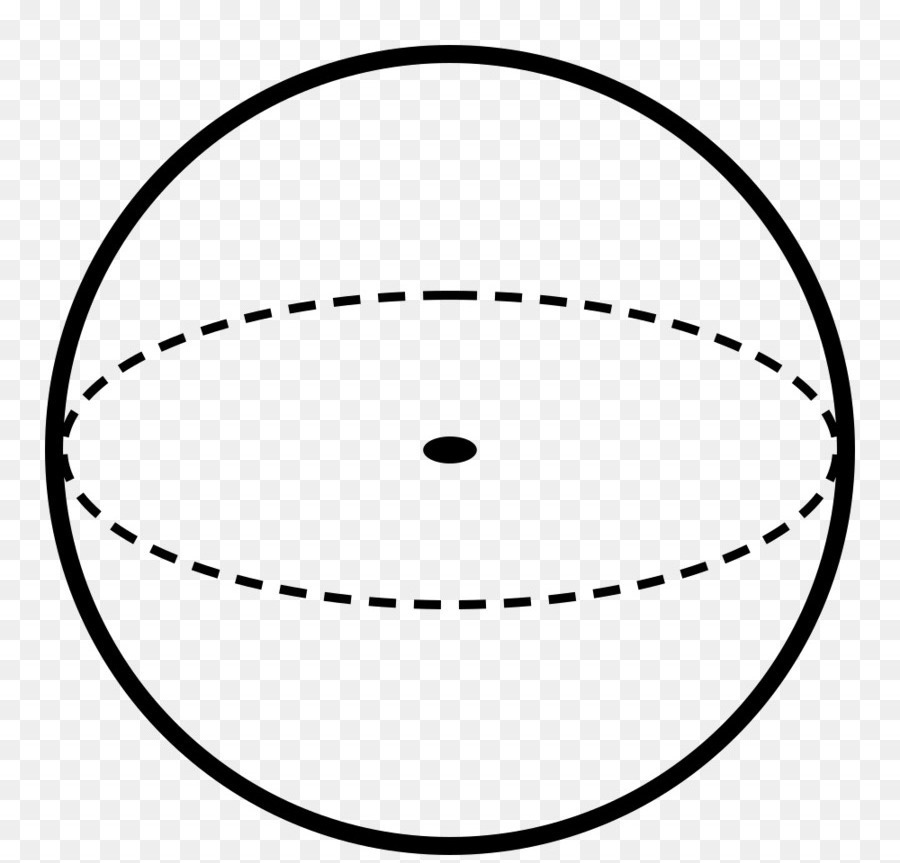
Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.
Сфера и шар: в чем разница и в чем сходство?
Часто школьники путают эти две фигуры, которые внешне похожи друг на друга, но обладают совершенно разными физическими свойствами. Сфера и шар в первую очередь отличаются своей массой: сфера — это бесконечно тонкий слой, шар же — это объемное тело конечной плотности, которая одинакова во всех его точках, ограниченных сферической поверхностью. То есть шар обладает конечной массой и является вполне реальным объектом. Сфера — это фигура идеальная, не имеющая массы, которая в действительности не существует, но она является удачной идеализацией в геометрии при изучении ее свойств.
Примерами реальных объектов, форма которых практически соответствует сфере, являются новогодняя игрушка в виде шарика для украшения елки или мыльный пузырь.

Что касается сходства между рассматриваемыми фигурами, то можно назвать следующие их признаки:
- обе они обладают одинаковой симметрией;
- для обеих формула площади поверхности является одинаковой, более того, они обладают равной площадью поверхности, если их радиусы равны;
- обе фигуры при равных радиусах занимают одинаковый объем в пространстве, только шар его заполняет полностью, а сфера лишь ограничивает своей поверхностью.
Сфера и шар равного радиуса приведены на рисунке ниже.
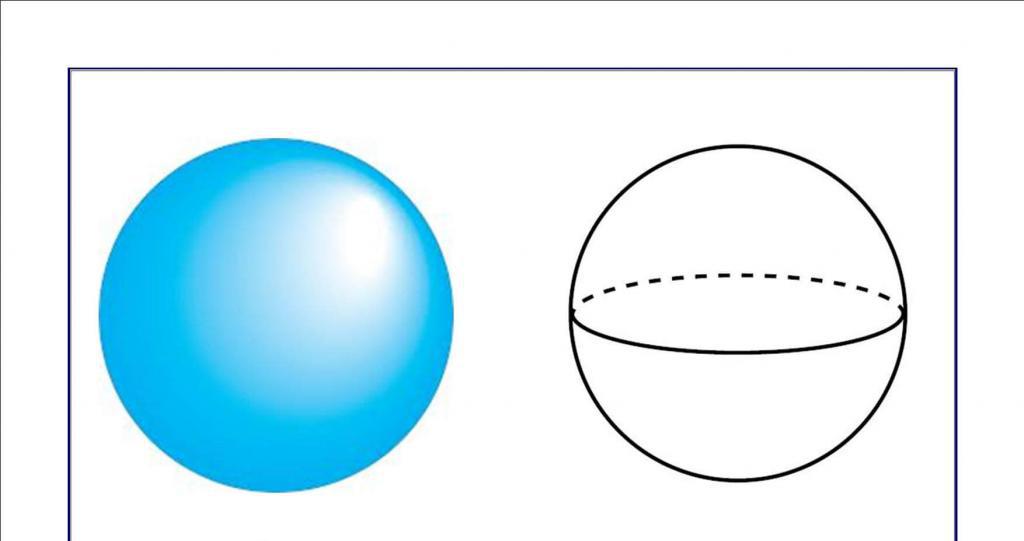
Заметим, что шар, так же как и сфера, является телом вращения, поэтому его можно получить, если вращать вокруг диаметра круг (не окружность!).
Элементы сферы
Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:
- Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
- Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
- Площадь поверхности S — двумерная характеристика, формула для которой будет приведена ниже.
- Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан — это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R2.
Геометрические свойства сферы
Из приведенного описания этой фигуры можно самостоятельно догадаться об этих свойствах. Они следующие:
- Любая прямая, которая пересекает сферу и проходит через ее центр, является осью симметрии фигуры. Поворот сферы вокруг этой оси на любой угол переводит ее в саму себя.
- Плоскость, которая пересекает рассматриваемую фигуру через ее центр, делит сферу на две равные части, то есть является плоскостью отражения.
Площадь поверхности фигуры
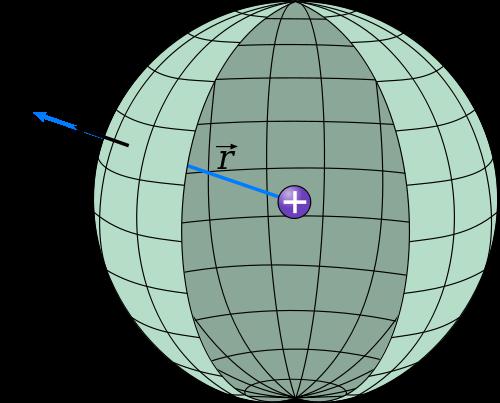
Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:
S = 4*pi*R2, где pi ≈ 3,1416.
Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:
S = pi*D2.
Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.
Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:
Ω = S/R2 = 4*pi*R2/R2 = 4*pi стерадиан.
Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.
Поверхность планеты Земля

Формулу сферы можно применить для определения площади поверхности планеты, на которой мы живем. Перед тем как приступать к вычислениям, следует сделать пару оговорок:
- Во-первых, Земля не обладает идеальной сферической поверхностью. Ее экваториальный и полярный радиусы равны 6378 км и 6357 км соответственно. Отличие между этими цифрами не превышает 0,3%, поэтому для расчета можно взять средний радиус 6371 км.
- Во-вторых, рельеф поверхности Земли является трехмерным, то есть на ней имеются впадины и горы. Эти характерные особенности планеты приводят к увеличению ее площади поверхности, тем не менее, в расчете их учитывать не будем, поскольку даже самая большая гора, Эверест, составляет 0,1% от земного радиуса (8,848/6371).
Используя формулу сферы, получаем:
S = 4*pi*R2 = 4*3,1416*63712 ≈ 510,066 млн. км2.
Россия, по официальным данным, занимает площадь 17,125 млн км2, что составляет 3,36% от поверхности планеты. Если же учесть, что к суше относятся лишь 150,387 млн км2, тогда площадь нашей страны составит 11,4% от всей территории, не покрытой водой.
fb.ru
Сфера — Википедия. Что такое Сфера
 Сфера (каркасная проекция)
Сфера (каркасная проекция) 
Сфе́ра (др.-греч. σφαῖρα «мяч, шар[1]») — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).
Свойства
Сфера является поверхностью вращения, образованной при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252,96 кв. градусов.
Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объём, также из всех поверхностей с данной площадью сфера ограничивает наибольший объём. Поэтому тела сферической формы встречаются в природе, например, маленькие капли воды при свободном падении приобретают сферическую форму именно из-за минимизации площади поверхности силой поверхностного натяжения.
Объём цилиндра, объём вписанного в него шара, касающегося обоих его оснований, и объём конуса, с вершиной в центре одного основания цилиндра и с основанием, совпадающим с другим основанием цилиндра, находятся в соотношении 3 : 2 : 1[2].
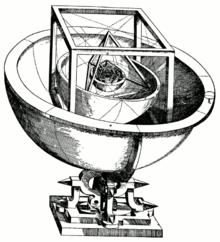 «Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.
«Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.Значение в естествознании
Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. У древних греков возникло представление о вращающейся хрустальной сфере, к которой прикреплены звёзды. Также в среде древнегреческих учёных появились космологические модели со сферической Землёй и прикреплёнными к вращающимся сферам из эфира планетами. Представления о вращающихся небесных сферах господствовали по крайней мере до средних веков и даже вошли в гелиоцентрическую систему мира Николая Коперника, который назвал свой основной труд «О вращении небесных сфер» (лат. De revolutionibus orbium coelestium).
Небесные сферы со времён Древней Греции были частью более общей концепции гармонии сфер о музыкально-астрономическом устройстве мира, куда также входило понятие «музыка сфер». Эта концепция также существовала как минимум до средневековья. У одного из известнейших астрономов, Иоганна Кеплера, сфера занимала центральное место во всей его системе религиозно-мистических представлений, он писал: «Образ триединого бога есть сферическая поверхность, а именно: бог-отец в центре, бог-сын — на поверхности и святой дух — в симметричном отношении между центром и описанной вокруг него сферической поверхностью»[3][4]. Одно из первых значительных сочинений Кеплера, «Тайна мироздания» (лат. Mysterium Cosmographicum), было посвящено параметрам небесных сфер, Кеплер считал, что он открыл замечательную связь между правильными многогранниками, которых только пять, и небесными сферами, являвшимися, по Кеплеру, описанными и вписанными сферами этих многогранников. Представления о гармонии сфер сыграли большую роль при открытии Кеплером третьего закона движений небесных тел (во всяком случае, могут рассматриваться как стимул к поиску астрономических соотношений)[5]. Однако у Кеплера небесные сферы являлись уже чисто математическими объектами, а не физически существующими телами. К тому времени Тихо Браге показал, что движение комет, в частности, Большой кометы 1577 года, несовместимо с существованием твердых небесных сфер[6]. Как удобная математическая модель, осталась одна небесная сфера, с помощью которой астрономы по сей день представляют видимые положения звезд и планет.
Основные геометрические формулы
- Площадь поверхности сферы
- S=4πr2=πd2.{\displaystyle S=4\pi r^{2}=\pi d^{2}.}
- Объём шара, ограниченного сферой
- V=43πr3.{\displaystyle V={\frac {4}{3}}\pi r^{3}.}
- Площадь сегмента сферы высоты H{\displaystyle H}
- S=2πrH{\displaystyle S=2\pi rH}.
Сфера в трёхмерном пространстве
Уравнение сферы в прямоугольной системе координат:
- (x−x0)2+(y−y0)2+(z−z0)2=R2,{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},}
где (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})} — координаты центра сферы, R{\displaystyle R} — её радиус.
Параметрическое уравнение сферы с центром в точке (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})}:
- {x=x0+R⋅sinθ⋅cosϕ,y=y0+R⋅sinθ⋅sinϕ,z=z0+R⋅cosθ,{\displaystyle {\begin{cases}x=x_{0}+R\cdot \sin \theta \cdot \cos \phi ,\\y=y_{0}+R\cdot \sin \theta \cdot \sin \phi ,\\z=z_{0}+R\cdot \cos \theta ,\\\end{cases}}}
где θ∈[0,π]{\displaystyle \theta \in [0,\pi ]} и ϕ∈[0,2π).{\displaystyle \phi \in [0,2\pi ).}
Гауссова кривизна сферы постоянна и равна 1/R².
Геометрия на сфере
Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие окружности являются геодезическими линиями на сфере; любые две из них пересекаются в двух точках. Иными словами, большие круги сферы являются аналогами прямых на плоскости, расстояние между точками на сфере — длина дуги проходящего через них большого круга. Углу же между прямыми на плоскости соответствует двугранный угол между плоскостями больших кругов. Многие теоремы геометрии на плоскости справедливы и в сферической геометрии, существуют аналоги теоремы синусов, теоремы косинусов для сферических треугольников. В то же время, существует немало отличий, например, в сферическом треугольнике сумма углов всегда больше 180 градусов, к трём признакам равенства треугольников добавляется их равенство по трём углам, у сферического треугольника может быть два и даже три прямых угла — например, у сферического треугольника, образованного экватором и меридианами 0° и 90°.
Расстояние между двумя точками на сфере
Если даны сферические координаты двух точек, то расстояние между ними можно найти так:
- L=R⋅arccos(cosθ1⋅cosθ2+sinθ1⋅sinθ2⋅cos(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\cos \theta _{1}\cdot \cos \theta _{2}+\sin \theta _{1}\cdot \sin \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}
Однако, если угол θ{\displaystyle \theta } задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:
- L=R⋅arccos(sinθ1⋅sinθ2+cosθ1⋅cosθ2⋅cos(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\sin \theta _{1}\cdot \sin \theta _{2}+\cos \theta _{1}\cdot \cos \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}
В этом случае θ1{\displaystyle \theta _{1}} и θ2{\displaystyle \theta _{2}} называются широтами, а ϕ1{\displaystyle \phi _{1}} и ϕ2{\displaystyle \phi _{2}} долготами.
n-мерная сфера
В общем случае уравнение (n-1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:
- ∑i=1n(xi−ai)2=r2,{\displaystyle \sum _{i=1}^{n}(x_{i}-a_{i})^{2}=r^{2},}
где (a1,…,an){\displaystyle (a_{1},…,a_{n})} — центр сферы, а r{\displaystyle r} — радиус.
Пересечением двух n-мерных сфер является n-1-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.
В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.
n-мерная инверсия переводит n-1-мерную сферу в n-1-мерную сферу или гиперплоскость.
См. также
Примечания
wiki.sc

