Кластеризация — это… Что такое Кластеризация?

Кластерный анализ (англ. Data clustering) — задача разбиения заданной выборки объектов (ситуаций) на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя.

Типология задач кластеризации

Типы входных данных

• Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми или нечисловыми.
• Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов обучающей выборки.

Цели кластеризации

• Понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).
• Сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
• Обнаружение новизны (англ. novelty detection). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.

Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии.

Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.

Классическим примером таксономии на основе сходства является биноминальная номенклатура живых существ, предложенная Карлом Линнеем в середине XVIII века. Аналогичные систематизации строятся во многих областях знания, чтобы упорядочить информацию о большом количестве объектов.

Методы кластеризации

Формальная постановка задачи кластеризации

Пусть 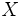 — множество объектов,  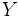— множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами 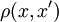. Имеется конечная обучающая выборка объектов

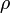. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике , а объекты разных кластеров существенно отличались. При этом каждому объекту приписывается номер кластера .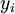

Алгоритм кластеризации — это функция 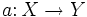, которая любому объекту 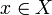ставит в соответствие номер кластера 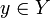. Множество 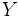в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.

Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки исходных объектов 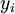 изначально не заданы, и даже может быть неизвестно само множество .

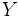Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:

• не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев,

а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты.

• число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием.
• результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом.

Применение

В биологии

В социологии

В информатике

• Группирование результатов поиска: Кластеризация используется для «интеллектуального» группирования результатов при поиске файлов, веб-сайтов, других объектов, предоставляя пользователю возможность быстрой навигации, выбора заведомо более релевантного подмножества и исключения заведомо менее релевантного — что может повысить юзабилити интерфейса по сравнению с выводом в виде простого сортированного по релевантности списка.
  • Clusty[1] — кластеризующая поисковая машина компании Vivísimo
  • поисковая система с автоматической кластеризацией результатов

• Сегментация изображений (image segmentation): Кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ (edge detection) или распознавания объектов.

• Интеллектуальный анализ данных (data mining):Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.

См. также

Литература

1. Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности. — М.: Финансы и статистика, 1989.
2. Журавлев Ю. И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
3. Загоруйко Н. Г. Прикладные методы анализа данных и знаний. — Новосибирск: ИМ СО РАН, 1999. ISBN 5-86134-060-9.
4. Мандель И. Д. Кластерный анализ. — М.: Финансы и статистика, 1988. ISBN 5-279-00050-7.
5. Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. — Киев: Наукова думка, 2004. ISBN 966-00-0341-2.
6. Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. — Springer, 2001. ISBN 0-387-95284-5.
7. Jain, Murty, Flynn Data clustering: a review. // ACM Comput. Surv. 31(3) , 1999

Внешние ссылки

На русском языке

На английском языке

• COMPACT — Comparative Package for Clustering Assessment. A free Matlab package, 2006.
• P. Berkhin, Survey of Clustering Data Mining Techniques, Accrue Software, 2002.
• Jain, Murty and Flynn: Data Clustering: A Review, ACM Comp. Surv., 1999.
• for another presentation of hierarchical, k-means and fuzzy c-means see this introduction to clustering. Also has an explanation on mixture of Gaussians.
• David Dowe, Mixture Modelling page — other clustering and mixture model links.
• a tutorial on clustering [2]
• The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay includes chapters on k-means clustering, soft k-means clustering, and derivations including the E-M algorithm and the variational view of the E-M algorithm.
• An overview of non-parametric clustering and computer vision
• «The Self-Organized Gene», tutorial explaining clustering through competitive learning and self-organizing maps.
• kernlab — R package for kernel based machine learning (includes spectral clustering implementation)
• Tutorial — Tutorial with introduction of Clustering Algorithms (k-means, fuzzy-c-means, hierarchical, mixture of gaussians) + some interactive demos (java applets)
• Data Mining Software — Data mining software frequently utilizes clustering techniques.
• Java Competitve Learning Application A suite of Unsupervised Neural Networks for clustering. Written in Java. Complete with all source code.
• Machine Learning Software — Also contains much clustering software.
• Fuzzy Clustering Algorithms and their Application to Medical Image Analysis PhD Thesis, 2001, by AI Shihab.
• Cluster Computing and MapReduce Lecture 4

Wikimedia Foundation. 2010.

Кластерный анализ — Википедия

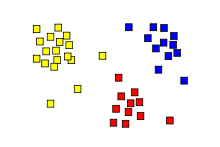Результат кластерного анализа обозначен раскрашиванием точек в соответствии с принадлежностью к одному из трёх кластеров.

Кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы^[1][2][3][4]. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя.

Большинство исследователей (см., напр.,^[5]) склоняются к тому, что впервые термин «кластерный анализ» (англ. cluster — гроздь, сгусток, пучок) был предложен математиком Р. Трионом^[6]. Впоследствии возник ряд терминов, которые в настоящее время принято считать синонимами термина «кластерный анализ»: автоматическая классификация, ботриология.

Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии, геологии и других дисциплинах. Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа.

Кластерный анализ выполняет следующие основные задачи:

• Разработка типологии или классификации.
• Исследование полезных концептуальных схем группирования объектов.
• Порождение гипотез на основе исследования данных.
• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы:

• Отбор выборки для кластеризации. Подразумевается, что имеет смысл кластеризовать только количественные данные.
• Определение множества переменных, по которым будут оцениваться объекты в выборке, то есть признакового пространства.
• Вычисление значений той или иной меры сходства (или различия) между объектами.
• Применение метода кластерного анализа для создания групп сходных объектов.
• Проверка достоверности результатов кластерного решения.

Можно встретить описание двух фундаментальных требований, предъявляемых к данным — однородность и полнота. Однородность требует, чтобы все кластеризуемые сущности были одной природы, описывались сходным набором характеристик

[7]. Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство — z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп). В противном случае выборку нужно корректировать.

Типы входных данных[править | править код]

• Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми или нечисловыми.
• Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов метрического пространства.
• Матрица сходства между объектами^[8]. Учитывается степень сходства объекта с другими объектами выборки в метрическом пространстве. Сходство здесь дополняет расстояние (различие) между объектами до 1.

В современной науке применяется несколько алгоритмов обработки входных данных. Анализ путём сравнения объектов, исходя из признаков, (наиболее распространённый в биологических науках) называется Q-типом анализа, а в случае сравнения признаков, на основе объектов — R-типом анализа. Существуют попытки использования гибридных типов анализа (например, RQ-анализ), но данная методология ещё должным образом не разработана.

Цели кластеризации[править | править код]

• Понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).
• Сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
• Обнаружение новизны (англ. novelty detection). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.

Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии. Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.

Методы кластеризации[править | править код]

Общепринятой классификации методов кластеризации не существует, но можно выделить ряд групп подходов (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации)^[9]:

1. Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k классов. Некоторые авторы (например, А. И. Орлов) считают, что данная группа вовсе не относится к кластеризации и противопоставляют её под названием «дискриминация», то есть выбор отнесения объектов к одной из известных групп (обучающих выборок).
2. Подходы на основе систем искусственного интеллекта: весьма условная группа, так как методов очень много и методически они весьма различны.
3. Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.
4. Теоретико-графовый подход.
5. Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие). По количеству признаков иногда выделяют монотетические и политетические методы классификации.
6. Другие методы. Не вошедшие в предыдущие группы.

Подходы 4 и 5 иногда объединяют под названием структурного или геометрического подхода, обладающего большей формализованностью понятия близости^[10]. Несмотря на значительные различия между перечисленными методами все они опираются на исходную «гипотезу компактности»: в пространстве объектов все близкие объекты должны относиться к одному кластеру, а все различные объекты соответственно должны находиться в различных кластерах.

Формальная постановка задачи кластеризации[править | править код]

Пусть X{\displaystyle X} — множество объектов, Y{\displaystyle Y} — множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами ρ(x,x′){\displaystyle \rho (x,x’)}. Имеется конечная обучающая выборка объектов Xm={x1,…,xm}⊂X{\displaystyle X^{m}=\{x_{1},\dots ,x_{m}\}\subset X}. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике ρ{\displaystyle \rho }, а объекты разных кластеров существенно отличались. При этом каждому объекту xi∈Xm{\displaystyle x_{i}\in X^{m}} приписывается номер кластера yi{\displaystyle y_{i}}.

Алгоритм кластеризации — это функция a:X→Y{\displaystyle a\colon X\to Y}, которая любому объекту x∈X{\displaystyle x\in X} ставит в соответствие номер кластера y∈Y{\displaystyle y\in Y}. Множество Y{\displaystyle Y} в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.

Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки исходных объектов yi{\displaystyle y_{i}} изначально не заданы, и даже может быть неизвестно само множество Y{\displaystyle Y}.

Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин (как считает ряд авторов):

• не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты. Следовательно, для определения качества кластеризации требуется эксперт предметной области, который бы мог оценить осмысленность выделения кластеров.
• число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием. Это справедливо только для методов дискриминации, так как в методах кластеризации выделение кластеров идёт за счёт формализованного подхода на основе мер близости.
• результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом. Но стоит отметить, что есть ряд рекомендаций к выбору мер близости для различных задач.

В биологии[править | править код]

В биологии кластеризация имеет множество приложений в самых разных областях. Например, в биоинформатике с помощью неё анализируются сложные сети взаимодействующих генов, состоящие порой из сотен или даже тысяч элементов. Кластерный анализ позволяет выделить подсети, узкие места, концентраторы и другие скрытые свойства изучаемой системы, что позволяет в конечном счете узнать вклад каждого гена в формирование изучаемого феномена.

В области экологии широко применяется для выделения пространственно однородных групп организмов, сообществ и т. п. Реже методы кластерного анализа применяются для исследования сообществ во времени. Гетерогенность структуры сообществ приводит к возникновению нетривиальных методов кластерного анализа (например, метод Чекановского).

В общем стоит отметить, что исторически сложилось так, что в качестве мер близости в биологии чаще используются меры сходства, а не меры различия (расстояния).

В социологии[править | править код]

При анализе результатов социологических исследований рекомендуется осуществлять анализ методами иерархического агломеративного семейства, а именно методом Уорда, при котором внутри кластеров оптимизируется минимальная дисперсия, в итоге создаются кластеры приблизительно равных размеров. Метод Уорда наиболее удачен для анализа социологических данных. В качестве меры различия лучше квадратичное евклидово расстояние, которое способствует увеличению контрастности кластеров. Главным итогом иерархического кластерного анализа является дендрограмма или «сосульчатая диаграмма». При её интерпретации исследователи сталкиваются с проблемой того же рода, что и толкование результатов факторного анализа — отсутствием однозначных критериев выделения кластеров. В качестве главных рекомендуется использовать два способа — визуальный анализ дендрограммы и сравнение результатов кластеризации, выполненной различными методами.

Визуальный анализ дендрограммы предполагает «обрезание» дерева на оптимальном уровне сходства элементов выборки. «Виноградную ветвь» (терминология Олдендерфера М. С. и Блэшфилда Р. К.^[11]) целесообразно «обрезать» на отметке 5 шкалы Rescaled Distance Cluster Combine, таким образом будет достигнут 80 % уровень сходства. Если выделение кластеров по этой метке затруднено (на ней происходит слияние нескольких мелких кластеров в один крупный), то можно выбрать другую метку. Такая методика предлагается Олдендерфером и Блэшфилдом.

Теперь возникает вопрос устойчивости принятого кластерного решения. По сути, проверка устойчивости кластеризации сводится к проверке её достоверности. Здесь существует эмпирическое правило — устойчивая типология сохраняется при изменении методов кластеризации. Результаты иерархического кластерного анализа можно проверять итеративным кластерным анализом по методу k-средних. Если сравниваемые классификации групп респондентов имеют долю совпадений более 70 % (более 2/3 совпадений), то кластерное решение принимается.

Проверить адекватность решения, не прибегая к помощи другого вида анализа, нельзя. По крайней мере, в теоретическом плане эта проблема не решена. В классической работе Олдендерфера и Блэшфилда «Кластерный анализ» подробно рассматриваются и в итоге отвергаются дополнительные пять методов проверки устойчивости:

1. кофенетическая корреляция — не рекомендуется и ограничена в использовании;
2. тесты значимости (дисперсионный анализ) — всегда дают значимый результат;
3. методика повторных (случайных) выборок, что, тем не менее, не доказывает обоснованность решения;
4. тесты значимости для внешних признаков пригодны только для повторных измерений;
5. методы Монте-Карло очень сложны и доступны только опытным математикам^{[источник не указан 2674 дня]}.

В информатике[править | править код]

• Кластеризация результатов поиска — используется для «интеллектуальной» группировки результатов при поиске файлов, веб-сайтов, других объектов, предоставляя пользователю возможность быстрой навигации, выбора заведомо более релевантного подмножества и исключения заведомо менее релевантного — что может повысить юзабилити интерфейса по сравнению с выводом в виде простого сортированного по релевантности списка.
• Сегментация изображений (англ. image segmentation) — кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ (англ. edge detection) или распознавания объектов.
• Интеллектуальный анализ данных (англ. data mining) — кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.

1. ↑ Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Классификация и снижение размерности. — М.: Финансы и статистика, 1989. — 607 с.
2. ↑ Мандель И. Д. Кластерный анализ. — М.: Финансы и статистика, 1988. — 176 с.
3. ↑ Хайдуков Д. С. Применение кластерного анализа в государственном управлении// Философия математики: актуальные проблемы. — М.: МАКС Пресс, 2009. — 287 с.
4. ↑ Классификация и кластер. Под ред. Дж. Вэн Райзина. М.: Мир, 1980. 390 с.
5. ↑ Мандель И. Д. Кластерный анализ. — М.: Финансы и статистика, 1988. — С. 10.
6. ↑ Tryon R.C. Cluster analysis. — London: Ann Arbor Edwards Bros, 1939. — 139 p.
7. ↑ Жамбю М. Иерархический кластер-анализ и соответствия. — М.: Финансы и статистика, 1988. — 345 с.
8. ↑ Дюран Б., Оделл П. Кластерный анализ. — М.: Статистика, 1977. — 128 с.
9. ↑ Бериков В. С., Лбов Г. С. Современные тенденции в кластерном анализе Архивная копия от 10 августа 2013 на Wayback Machine // Всероссийский конкурсный отбор обзорно-аналитических статей по приоритетному направлению «Информационно-телекоммуникационные системы», 2008. — 26 с.
10. ↑ Вятченин Д. А. Нечёткие методы автоматической классификации. — Минск: Технопринт, 2004. — 219 с.
11. ↑ Олдендерфер М. С., Блэшфилд Р. К. Кластерный анализ / Факторный, дискриминантный и кластерный анализ: пер. с англ.; Под. ред. И. С. Енюкова. — М.: Финансы и статистика, 1989—215 с.

На русском языке

• www.MachineLearning.ru — профессиональный вики-ресурс, посвященный машинному обучению и интеллектуальному анализу данных

На английском языке

• COMPACT — Comparative Package for Clustering Assessment. A free Matlab package, 2006.
• P. Berkhin, Survey of Clustering Data Mining Techniques, Accrue Software, 2002.
• Jain, Murty and Flynn: Data Clustering: A Review, ACM Comp. Surv., 1999.
• for another presentation of hierarchical, k-means and fuzzy c-means see this introduction to clustering. Also has an explanation on mixture of Gaussians.
• David Dowe, Mixture Modelling page — other clustering and mixture model links.
• a tutorial on clustering [1]  (недоступная ссылка с 13-05-2013 [2431 день] — история)
• The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay includes chapters on k-means clustering, soft k-means clustering, and derivations including the E-M algorithm and the variational view of the E-M algorithm.
• An overview of non-parametric clustering and computer vision
• «The Self-Organized Gene», tutorial explaining clustering through competitive learning and self-organizing maps.
• kernlab  (недоступная ссылка с 13-05-2013 [2431 день] — история) — R package for kernel based machine learning (includes spectral clustering implementation)
• Tutorial — Tutorial with introduction of Clustering Algorithms (k-means, fuzzy-c-means, hierarchical, mixture of gaussians) + some interactive demos (java applets)
• Data Mining Software — Data mining software frequently utilizes clustering techniques.
• Java Competitve Learning Application  (недоступная ссылка с 13-05-2013 [2431 день] — история) A suite of Unsupervised Neural Networks for clustering. Written in Java. Complete with all source code.
• Machine Learning Software — Also contains much clustering software.
• Fuzzy Clustering Algorithms and their Application to Medical Image Analysis PhD Thesis, 2001, by AI Shihab.
• Cluster Computing and MapReduce Lecture 4
• PyClustering Library — Python library contains clustering algorithms (C++ source code can be also used — CCORE part of the library) and collection of neural and oscillatory networks with examples and demos.

Обзор алгоритмов кластеризации данных / Habr

Приветствую!

В своей дипломной работе я проводил обзор и сравнительный анализ алгоритмов кластеризации данных. Подумал, что уже собранный и проработанный материал может оказаться кому-то интересен и полезен.
О том, что такое кластеризация, рассказал sashaeve в статье «Кластеризация: алгоритмы k-means и c-means». Я частично повторю слова Александра, частично дополню. Также в конце этой статьи интересующиеся могут почитать материалы по ссылкам в списке литературы.

Так же я постарался привести сухой «дипломный» стиль изложения к более публицистическому.

Понятие кластеризации

Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.

Применение кластерного анализа в общем виде сводится к следующим этапам:

1. Отбор выборки объектов для кластеризации.
2. Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных.
3. Вычисление значений меры сходства между объектами.
4. Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
5. Представление результатов анализа.

После получения и анализа результатов возможна корректировка выбранной метрики и метода кластеризации до получения оптимального результата.

Меры расстояний

Итак, как же определять «похожесть» объектов? Для начала нужно составить вектор характеристик для каждого объекта — как правило, это набор числовых значений, например, рост-вес человека. Однако существуют также алгоритмы, работающие с качественными (т.н. категорийными) характеристиками.

После того, как мы определили вектор характеристик, можно провести нормализацию, чтобы все компоненты давали одинаковый вклад при расчете «расстояния». В процессе нормализации все значения приводятся к некоторому диапазону, например, [-1, -1] или [0, 1].

Наконец, для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик, вот лишь основные из них:

1. Евклидово расстояние
   Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:
   
   
2. Квадрат евклидова расстояния
   Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
   
   
3. Расстояние городских кварталов (манхэттенское расстояние)
   Это расстояние является средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако для этой меры влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:
   
   
4. Расстояние Чебышева
   Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой-либо одной координате. Расстояние Чебышева вычисляется по формуле:
   
   
5. Степенное расстояние
   Применяется в случае, когда необходимо увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле:
   ,
   где r и p – параметры, определяемые пользователем. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра – r и p — равны двум, то это расстояние совпадает с расстоянием Евклида.

Выбор метрики полностью лежит на исследователе, поскольку результаты кластеризации могут существенно отличаться при использовании разных мер.

Классификация алгоритмов

Для себя я выделил две основные классификации алгоритмов кластеризации.

1. Иерархические и плоские.
   Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.о. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.
   Плоские алгоритмы строят одно разбиение объектов на кластеры.
2. Четкие и нечеткие.
   Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.

Объединение кластеров

В случае использования иерархических алгоритмов встает вопрос, как объединять между собой кластера, как вычислять «расстояния» между ними. Существует несколько метрик:

1. Одиночная связь (расстояния ближайшего соседа)
   В этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Результирующие кластеры имеют тенденцию объединяться в цепочки.
   
2. Полная связь (расстояние наиболее удаленных соседей)
   В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. наиболее удаленными соседями). Этот метод обычно работает очень хорошо, когда объекты происходят из отдельных групп. Если же кластеры имеют удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.
   
3. Невзвешенное попарное среднее
   В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных («цепочечного» типа) кластеров.
   
4. Взвешенное попарное среднее
   Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому данный метод должен быть использован, когда предполагаются неравные размеры кластеров.
   
5. Невзвешенный центроидный метод
   В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.
   
6. Взвешенный центроидный метод (медиана)
   Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учета разницы между размерами кластеров. Поэтому, если имеются или подозреваются значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
   

Обзор алгоритмов

Алгоритмы иерархической кластеризации

Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры. Более распространены восходящие алгоритмы, которые в начале работы помещают каждый объект в отдельный кластер, а затем объединяют кластеры во все более крупные, пока все объекты выборки не будут содержаться в одном кластере. Таким образом строится система вложенных разбиений. Результаты таких алгоритмов обычно представляют в виде дерева – дендрограммы. Классический пример такого дерева – классификация животных и растений.

Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью (см. обзор мер расстояний между кластерами).

К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.

Алгоритмы квадратичной ошибки

Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:

где c_j — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).

Алгоритмы квадратичной ошибки относятся к типу плоских алгоритмов. Самым распространенным алгоритмом этой категории является метод k-средних. Этот алгоритм строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:

1. Случайно выбрать k точек, являющихся начальными «центрами масс» кластеров.
2. Отнести каждый объект к кластеру с ближайшим «центром масс».
3. Пересчитать «центры масс» кластеров согласно их текущему составу.
4. Если критерий остановки алгоритма не удовлетворен, вернуться к п. 2.

В качестве критерия остановки работы алгоритма обычно выбирают минимальное изменение среднеквадратической ошибки. Так же возможно останавливать работу алгоритма, если на шаге 2 не было объектов, переместившихся из кластера в кластер.

К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.

Нечеткие алгоритмы

Наиболее популярным алгоритмом нечеткой кластеризации является алгоритм c-средних (c-means). Он представляет собой модификацию метода k-средних. Шаги работы алгоритма:

1. Выбрать начальное нечеткое разбиение n объектов на k кластеров путем выбора матрицы принадлежности U размера n x k.
2. Используя матрицу U, найти значение критерия нечеткой ошибки:
   ,
   где c_k — «центр масс» нечеткого кластера k:
   .
3. Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
4. Возвращаться в п. 2 до тех пор, пока изменения матрицы U не станут незначительными.

Этот алгоритм может не подойти, если заранее неизвестно число кластеров, либо необходимо однозначно отнести каждый объект к одному кластеру.

Алгоритмы, основанные на теории графов

Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа G=(V, E), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность вносения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации.

Алгоритм выделения связных компонент

В алгоритме выделения связных компонент задается входной параметр R и в графе удаляются все ребра, для которых «расстояния» больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры.

Для подбора параметра R обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика – один соответствует внутрикластерным расстояниям, второй – межкластерным расстояния. Параметр R подбирается из зоны минимума между этими пиками. При этом управлять количеством кластеров при помощи порога расстояния довольно затруднительно.

Алгоритм минимального покрывающего дерева

Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом. На рисунке изображено минимальное покрывающее дерево, полученное для девяти объектов.

Путём удаления связи, помеченной CD, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: {A, B, C} и {D, E, F, G, H, I}. Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра EF, которое имеет длину, равную 4,5 единицам.

Послойная кластеризация

Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния c. Например, если расстояние между объектами , то .

Алгоритм послойной кластеризации формирует последовательность подграфов графа G, которые отражают иерархические связи между кластерами:

,

где G^t = (V, E^t) — граф на уровне с^t,
,
с^t – t-ый порог расстояния,
m – количество уровней иерархии,
G⁰ = (V, o), o – пустое множество ребер графа, получаемое при t⁰ = 1,
G^m = G, то есть граф объектов без ограничений на расстояние (длину ребер графа), поскольку t^m = 1.

Посредством изменения порогов расстояния {с⁰, …, с^m}, где 0 = с⁰ < с¹ < …< с^m = 1, возможно контролировать глубину иерархии получаемых кластеров. Таким образом, алгоритм послойной кластеризации способен создавать как плоское разбиение данных, так и иерархическое.

Сравнение алгоритмов

Вычислительная сложность алгоритмов

Алгоритм кластеризации	Вычислительная сложность
Иерархический	O(n2)
k-средних	O(nkl), где k – число кластеров, l – число итераций
c-средних
Выделение связных компонент	зависит от алгоритма
Минимальное покрывающее дерево	O(n2 log n)
Послойная кластеризация	O(max(n, m)), где m < n(n-1)/2

Сравнительная таблица алгоритмов

Алгоритм кластеризации	Форма кластеров	Входные данные	Результаты
Иерархический	Произвольная	Число кластеров или порог расстояния для усечения иерархии	Бинарное дерево кластеров
k-средних	Гиперсфера	Число кластеров	Центры кластеров
c-средних	Гиперсфера	Число кластеров, степень нечеткости	Центры кластеров, матрица принадлежности
Выделение связных компонент	Произвольная	Порог расстояния R	Древовидная структура кластеров
Минимальное покрывающее дерево	Произвольная	Число кластеров или порог расстояния для удаления ребер	Древовидная структура кластеров
Послойная кластеризация	Произвольная	Последовательность порогов расстояния	Древовидная структура кластеров с разными уровнями иерархии

Немного о применении

В своей работе мне нужно было из иерархических структур (деревьев) выделять отдельные области. Т.е. по сути необходимо было разрезать исходное дерево на несколько более мелких деревьев. Поскольку ориентированное дерево – это частный случай графа, то естественным образом подходят алгоритмы, основанными на теории графов.

В отличие от полносвязного графа, в ориентированном дереве не все вершины соединены ребрами, при этом общее количество ребер равно n–1, где n – число вершин. Т.е. применительно к узлам дерева, работа алгоритма выделения связных компонент упростится, поскольку удаление любого количества ребер «развалит» дерево на связные компоненты (отдельные деревья). Алгоритм минимального покрывающего дерева в данном случае будет совпадать с алгоритмом выделения связных компонент – путем удаления самых длинных ребер исходное дерево разбивается на несколько деревьев. При этом очевидно, что фаза построения самого минимального покрывающего дерева пропускается.

В случае использования других алгоритмов в них пришлось бы отдельно учитывать наличие связей между объектами, что усложняет алгоритм.

Отдельно хочу сказать, что для достижения наилучшего результата необходимо экспериментировать с выбором мер расстояний, а иногда даже менять алгоритм. Никакого единого решения не существует.

Список литературы

1. Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. Курс лекций. МГУ, 2007.
2. Jain A., Murty M., Flynn P. Data Clustering: A Review. // ACM Computing Surveys. 1999. Vol. 31, no. 3.
3. Котов А., Красильников Н. Кластеризация данных. 2006.
3. Мандель И. Д. Кластерный анализ. — М.: Финансы и Статистика, 1988.
4. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989.
5. Информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных — www.machinelearning.ru
6. Чубукова И.А. Курс лекций «Data Mining», Интернет-университет информационных технологий — www.intuit.ru/department/database/datamining

кластеризация — Викисловарь

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	кластериза́ция	кластериза́ции
Р.	кластериза́ции	кластериза́ций
Д.	кластериза́ции	кластериза́циям
В.	кластериза́цию	кластериза́ции
Тв.	кластериза́цией кластериза́циею	кластериза́циями
Пр.	кластериза́ции	кластериза́циях

клас-те-ри-за́-ци·я

Существительное, неодушевлённое, женский род, 1-е склонение (тип склонения 7a по классификации А. А. Зализняка).

Корень: —.

Произношение[править]

• МФА: [kɫəstɛrʲɪˈzat͡sɨɪ̯ə]

Семантические свойства[править]

Значение[править]

1. группировка, разбиение множества объектов на непересекающиеся подмножества, кластеры, состоящие из схожих объектов ◆ Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. ВП, «w:Кластерный анализ»

Синонимы[править]

Антонимы[править]

Гиперонимы[править]

1. разбиение

Гипонимы[править]

Родственные слова[править]

Этимология[править]

Происходит от ??

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Библиография[править]

Перекластеризация что это | Что делать если трафик уменьшился

Привет! Сегодня решил написать про одну интересную проблему — падение посещаемости из органической выдачи и что с этим делать. Нередко бывает, что качественный в техническом плане ресурс, который не использует какие-либо запрещенные техники стабильно  теряет посещаемость, а сайт у которого множество проблем растет. Встречали такое? И часто причина падения трафика на качественном ресурсе совсем не очевидна.

Причем перекластеризация запросов, покупка качественных ссылок и другие типовые манипуляции тут не помогают. Потери трафика невелики, но общая динамика стабильно отрицательна. Поддержка Яндекс же отвечает, что с сайтом все хорошо, в панели вебмастера  Яндекс и Гугл нет никаких аномалий и владелец проекта никак не может выяснить, что же произошло с его детищем. Возможно, данная ситуация вам знакома?!

Кстати, как написать в службы поддержки Яндекс и Гугл я подробно разбирал в данной статье. Также, чтобы повысить посещаемость необходимо пройти все этапы поисковой оптимизации сайта, которые я описывал ранее.

А бывает и наоборот — в один день сайт может потерять практически все переходы с одной из поисковых систем!

Источников проблем у сайта великое множество, но большинство из них явно себя проявляют и их легко детектировать, например часть страниц попала под Баден или на сайт наложили фильтр за ссылки и так далее. В большинстве случаев провалы трафика заметны невооруженным глазом и далее остается просто детально изучить аналитику под разными срезами. Сегодня мы рассмотрим различные случаи, когда сайт начинает терять посещаемость из поиска.

А может это просто сезонность?

Итак, мы имеем наглядную просадку поисковых переходов на проекте и надо первым делом однозначно убедиться в том, что проблема действительно есть. Бывает так, что посещаемость и позиции просели, но причиной этого послужили не проблемы в оптимизации, а банальная сезонность тематики или основных запросов по которым сайт в ТОП. Быстро проверить сезонность вашей тематике можно в Wordstat во вкладке — «история запросов»:

 

Динамика популярности запроса про мангалы

Как видно на скриншоте — поисковый запрос «купить мангал» имеет ярко выраженную сезонность и спад трафика в зимнее время обусловлен не проблемами сайта, а уменьшением общего объема трафика, генерируемого данной тематикой.

Или летняя просадка?

Еще одна частая причина того что упал трафик кроется в общей просадке трафика из поисковых систем в летний период. Сам по себе сезон сильно влияет на объем генерируемых поиском переходов! Стоит понимать, что летом общий уровень трафика из поисковиков падает практически в 2 раза, особенно заметно это становится у проектов без сезонности. То есть то, что ваш сайт в летний период может потерять до половины переходов так же не является аномалией, подробнее увидеть общую динамику поискового трафика в Рунете можно на следующем скриншоте:

 

 

В живую посмотреть этот и другие интересные графики вы можете по ссылке.

Грубые нарушения регламента ПС

Итак, в прошлой главе мы определились с тем, что падение трафика не вызвано сезонностью и следующим пунктом проверки является проверка сайта на грубые нарушения регламента поисковых систем.

Первым делом переходим в Панель «Яндекс.Вебмастер» и изучаем оповещения:

Если подобных сообщений в панели вебмастера не обнаружено идем дальше. Заходим в панель вебмастеров Гугл и выбираем вкладку — «санкции, принятые вручную»:

 

Следующим этапом проверки на грубые нарушения стоит написать в поддержку Яндекс, где детально рассказать о провале посещаемости и спросить — «Добрый день, уважаемые Платоны. Подскажите, нет ли на моем сайте понижающих фильтров, т.к. Метрика показывает явный тренд спада посещаемости, а запросы … ухудшили свои позиции в serp». Чтобы написать в поддержку Яндекс необходимо нажать на соответствующую кнопку в самом низу интерфейса «Яндекс.Вебмастер» :

 

В большинстве случаев поддержка напишет вам о проблемах, если они есть, за одним исключением — фильтр Яндекс NoName, хотя я давно его уже не встречал.

Суть данного фильтра переоптимизация элементов ресурса, например меню, картинок, кода. Когда в теги ALT и TITLE картинок добавляют ключевые слова, когда даже у ссылок прописывают тег title с ключевым словом (привет перелинковке времен Снежинска), когда в меню стараются использовать как можно больше ключей, когда ключи используют даже в тех картинках, которые формируют дизайн. В таком случае на сайт накладывается фильтр noname, отличительной особенностью которого является полное молчание поддержки Яндекс, то есть они не признают наличие фильтра и говорят развивать ресурс дальше, хотя пессимизация очевидна. Для выхода из под фильтра приходится пересобрать весь сайт заново.

 

Если советы выше не помогли найти причину спада посещаемости — начинаем копать глубже.

Сопоставляем даты наложения санкций

Еще один интересный метод обнаружения и фиксации понижающих фильтров —0 четко определить дату начала падения и сопоставить с датами выхода основных фильтров поисковых систем. Для использования данной методики  переходим в метрику, во вкладку Отчеты -> Стандартные отчеты -> Источники — > Поисковые системы. Выбираем в  Метрике даты начала и конца анализируемого периода. В зависимости от размера среза, детализацию ставим по неделям или месяцам:

 

 

Определив дату наложения фильтра стоит сопоставить ее с известными датами релизов поисковых алгоритмов и ситуация может проясниться!

Сайт низкого качества

Грубое нарушение регламента поисковых роботов приводит к резким и явным провалам трафика, которые легко заметить, но бывает, что сайт никогда и не набирал трафика, т.к. с самого начала находился под понижающими фильтрами за низкое качество. Сайт низкого качества определить достаточно легко, он имеет много битых и внешних ссылок (проверяем через  бесплатную программу Xenu) и большие проблемы с индексацией. Про индексацию подробней писал тут. Нередко такой сайт имеет плохую внутреннюю перелинковку, которая концентрирует весь вес на мусорных страницах.

Если вы обнаружили разницу в индексации между Яндекс и Гугл в несколько раз да еще и много внешних ссылок, которые вы сами, вероятно даже и не ставили (сайт мог быть взломан вирусом, который наплодил тысячи страниц) — порядок дальнейших действий становится очевиден. Необходимо вычистить весь мусор и привести индексацию в порядок. Ранее писал про работу над одним из таких сайтов.

Чтобы избежать взлома сайта и размещения спамных ссылок — регулярно обновляйте движок (CMS) своего сайта.

Проблемы хостинга

Сразу несколько причин падения трафика можно связать с хостингом. Наиболее явными из них является периодическая недоступность и низкая скорость загрузки. Причем та скорость, которую вы видите у себя на компьютере совершенно ничего не показывает. И это не абстрактная фраза — даже если ваш проект открывается у вас очень быстро/очень медленно это не является совершенно никаким показателем скорости и это важно! Нередко мне доводилось встречать людей, которые свято верили в то, что если сайт у них быстро открывается, значит и поисковики так же считают, отнюдь. Скорость, как ее видят роботы, складывается из множества параметров, среди которых и пинг до целевой аудитории сайта. Наиболее адекватно оценить скорость поможет тест Google PageSpeed:

По этому тесту ваш сайт как минимум должен попадать в оранжевую зону!

Помимо классической скорости работы и тесту Гугл есть очень важный параметр — скорость открытия ресурса у пользователей из целевого региона, например, если вашему сайту присвоен регион Москва — не имеет особого значения то, как быстро он работает в Санкт-Петербурге и уж совсем не важно с какой скоростью он открывается у вас, важна именно скорость в целевом регионе. Нередко сервер на котором расположен сайт, находится за рубежом, что вызывает большие задержки при обмене данными между сервером и пользователем. И именно этот фактор может служить причиной очень интересной и распространенной проблемы — долговременное, медленное, но планомерное уменьшение трафика из поисковиков.

В настоящее время я готовлю очень подробное руководство по подготовке наиболее эффективной SEO статьи и планирую завершить его в течении нескольких недель, так что подписывайтесь на авторские материалы блога.

 

Акция на комплексный SEO тариф + настройка Директ и РСЯ

Бонусом к этой статье запускаю акцию, в рамках которой возьму один сайт на комплексный тариф по настройке контекстной рекламы и SEO, так что уже сейчас можете оставлять заявки. В тариф войдет:

1. сбор семантики
2. кластеризация запросов
3. семантическое проектирование (построение структуры сайта на основе кластеров семантики). Подробнее в руководстве
4. подготовка сео текстов
5. настройка рекламы Директ
6. настройка РСЯ
7. и другое

 

Результат прошлого проекта на аналогичном тарифе:

В все это с оптовой скидкой, так что >>> оставляйте заявки <<< (не забудьте указать, что это заявка по акции). Возьму только 1 сайт, так что не стоит тянуть

 

 

Создание кластеризатора — Технологии Яндекса

\n»,»clusterer_create.js»:»ymaps.ready(function () {\n var myMap = new ymaps.Map(‘map’, {\n center: [55.751574, 37.573856],\n zoom: 9,\n behaviors: [‘default’, ‘scrollZoom’]\n }, {\n searchControlProvider: ‘yandex#search’\n }),\n /**\n * Создадим кластеризатор, вызвав функцию-конструктор.\n * Список всех опций доступен в документации.\n * @see https://api.yandex.ru/maps/doc/jsapi/2.1/ref/reference/Clusterer.xml#constructor-summary\n */\n clusterer = new ymaps.Clusterer({\n /**\n * Через кластеризатор можно указать только стили кластеров,\n * стили для меток нужно назначать каждой метке отдельно.\n * @see https://api.yandex.ru/maps/doc/jsapi/2.1/ref/reference/option.presetStorage.xml\n */\n preset: ‘islands#invertedVioletClusterIcons’,\n /**\n * Ставим true, если хотим кластеризовать только точки с одинаковыми координатами.\n */\n groupByCoordinates: false,\n /**\n * Опции кластеров указываем в кластеризаторе с префиксом \»cluster\».\n * @see https://api.yandex.ru/maps/doc/jsapi/2.1/ref/reference/ClusterPlacemark.xml\n */\n clusterDisableClickZoom: true,\n clusterHideIconOnBalloonOpen: false,\n geoObjectHideIconOnBalloonOpen: false\n }),\n /**\n * Функция возвращает объект, содержащий данные метки.\n * Поле данных clusterCaption будет отображено в списке геообъектов в балуне кластера.\n * Поле balloonContentBody — источник данных для контента балуна.\n * Оба поля поддерживают HTML-разметку.\n * Список полей данных, которые используют стандартные макеты содержимого иконки метки\n * и балуна геообъектов, можно посмотреть в документации.\n * @see https://api.yandex.ru/maps/doc/jsapi/2.1/ref/reference/GeoObject.xml\n */\n getPointData = function (index) {\n return {\n balloonContentHeader: ‘Здесь может быть ваша ссылка‘,\n balloonContentBody: ‘

Ваше имя:

Телефон в формате 2xxx-xxx:

‘,\n balloonContentFooter: ‘Информация предоставлена: балуном метки ‘ + index + ‘‘,\n clusterCaption: ‘метка ‘ + index + ‘‘\n };\n },\n /**\n * Функция возвращает объект, содержащий опции метки.\n * Все опции, которые поддерживают геообъекты, можно посмотреть в документации.\n * @see https://api.yandex.ru/maps/doc/jsapi/2.1/ref/reference/GeoObject.xml\n */\n getPointOptions = function () {\n return {\n preset: ‘islands#violetIcon’\n };\n },\n points = [\n [55.831903,37.411961], [55.763338,37.565466], [55.763338,37.565466], [55.744522,37.616378], [55.780898,37.642889], [55.793559,37.435983], [55.800584,37.675638], [55.716733,37.589988], [55.775724,37.560840], [55.822144,37.433781], [55.874170,37.669838], [55.716770,37.482338], [55.780850,37.750210], [55.810906,37.654142], [55.865386,37.713329], [55.847121,37.525797], [55.778655,37.710743], [55.623415,37.717934], [55.863193,37.737000], [55.866770,37.760113], [55.698261,37.730838], [55.633800,37.564769], [55.639996,37.539400], [55.690230,37.405853], [55.775970,37.512900], [55.775777,37.442180], [55.811814,37.440448], [55.751841,37.404853], [55.627303,37.728976], [55.816515,37.597163], [55.664352,37.689397], [55.679195,37.600961], [55.673873,37.658425], [55.681006,37.605126], [55.876327,37.431744], [55.843363,37.778445], [55.875445,37.549348], [55.662903,37.702087], [55.746099,37.434113], [55.838660,37.712326], [55.774838,37.415725], [55.871539,37.630223], [55.657037,37.571271], [55.691046,37.711026], [55.803972,37.659610], [55.616448,37.452759], [55.781329,37.442781], [55.844708,37.748870], [55.723123,37.406067], [55.858585,37.484980]\n ],\n geoObjects = [];\n\n /**\n * Данные передаются вторым параметром в конструктор метки, опции — третьим.\n * @see https://api.yandex.ru/maps/doc/jsapi/2.1/ref/reference/Placemark.xml#constructor-summary\n */\n for(var i = 0, len = points.length; i clusterer_create.jsclusterer_create.html

Кластеризация Википедия

Результат кластерного анализа обозначен раскрашиванием точек в соответствии с принадлежностью к одному из трёх кластеров.

Кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы^[1][2][3][4]. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя.

Большинство исследователей (см., напр.,^[5]) склоняются к тому, что впервые термин «кластерный анализ» (англ. cluster — гроздь, сгусток, пучок) был предложен математиком Р. Трионом^[6]. Впоследствии возник ряд терминов, которые в настоящее время принято считать синонимами термина «кластерный анализ»: автоматическая классификация, ботриология.

Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии, геологии и других дисциплинах. Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа.

Задачи и условия[ | ]

Кластерный анализ выполняет следующие основные задачи:

• Разработка типологии или классификации.
• Исследование полезных концептуальных схем группирования объектов.
• Порождение гипотез на основе исследования данных.
• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы:

• Отбор выборки для кластеризации. Подразумевается, что имеет смысл кластеризовать только количественные данные.
• Определение множества переменных, по которым будут оцениваться объекты в выборке, то есть признакового пространства.
• Вычисление значений той или иной меры сходства (или различия) между объектами.
• Применение метода кластерного анализа для создания групп сходных объектов.
• Проверка достоверности результатов кластерного решения.

Можно встретить описание двух фундаментальных требований, предъявляемых к данным — однородность и полнота. Однородность требует, чтобы все кластеризуемые сущности были одной природы, описывались сходным набором характеристик^[7]. Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство — z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп). В противном случае выборку нужно корректировать.

Типология задач кластеризации[ | ]

Типы входных данных[