18 интересных фактов о геометрии > Точка-ру
Интересные факты о геометрии – это отличная возможность узнать больше о точных науках. Геометрия начала развиваться еще тысячи лет назад. Древним ученым удалось вывести немало основополагающих формул, которыми мы пользуемся и сегодня.
Итак, перед вами самые интересные факты о геометрии.
- Геометрия, как систематическая наука, возникла в Древней Греции.
- Одним из самых выдающихся ученых в области геометрии является Евклид. Открытые им законы и принципы до сих пор лежат в основе данной науки.
- Более 5 тысячелетий назад древние египтяне использовали геометрические знания при постройке пирамид, а также в ходе разметки земельных участков на побережьях Нила (см. интересные факты о Ниле).
- Знаете ли вы, что над дверью в академию, в которой Платон обучал своих последователей, находился следующая надпись: «Пусть не входит сюда тот, кто не знает геометрии»?
- Трапеция – одна из геометрических фигур, происходит от древнегреческого «трапезион», что буквально переводится, как – «столик».

- Среди всех геометрических форм с одинаковым периметром, круг обладает самой большой площадью.
- Посредством геометрических формул и не исключая того, что наша планета является сферой, древнегреческий ученый Эратосфен вычислил длину ее окружности. Интересен факт, что современные измерения показали, что грек выполнил все расчеты правильно, допустив лишь небольшую погрешность.
- В геометрии Лобачевского сумма всех углов треугольника менее 180⁰.
- Сегодня математикам известно о других разновидностях неевклидовых геометрий. Они не пpaктикуются в повседневной жизни, но помогают разрешить массу вопросов в других точных науках.
- Древнегреческое слово «конус» переводится, как – «сосновая шишка».
- Основы фpaктальной геометрии были заложены гениальным Леонардо да Винчи (см. интересные факты о Леонардо да Винчи).
- После того, как Пифагор вывел свою теорему он и его ученики испытали такое потрясение, что решили будто мир уже познан и осталось только объяснить его числами.

- Главным среди всех своих достижений Архимед считал вычисление объемов конуса и шара, вписанных в цилиндр. Объем конуса составляет 1/3 от объема цилиндра, в то время как объем шара – 2/3.
- В геометрии Римана сумма углов треугольника всегда превышает 180⁰.
- Интересен факт, что Евклид самостоятельно доказал 465 геометрических теорем.
- Оказывается, Наполеон Бонапарт был талантливым математиком, который за годы своей жизни написал немало научных трудов. Любопытно, что его именем названа одна из геометрических задач.
- В геометрии формула, помогающая измерить объем усеченной пирамиды появилась раньше, чем формула для целой пирамиды.
- В честь геометрии назван астероид под номером 376.
Димаш Кудайбергенов — биография и фото
Димаш Кудайбергенов – казахский певец и композитор, умеющий играть на многих инструментах. Обладатель многих престижных премий и победитель нескольких. ..
..
18 09 2022 22:16:55
Развитие капитализма
В конце 15 – начале 16 веков жизнь Западной Европы была отмечена столь ощутимыми переменами – ростом производства, торговли, расцветом культуры и познания…
17 09 2022 20:28:50
18 интересных фактов о Достоевском
Интересные факты о Достоевском – это отличная возможность узнать больше о творчестве русского писателя. Его произведения оказали большое влияние на…
16 09 2022 10:59:49
Самое высокое здание в мире – Интересные факты
Представляем вашему вниманию самое высокое здание в мире. Может вы думаете, что это Останкинская башня? Нет, она является высочайшим сооружением в Европе,…
15 09 2022 0:15:15
Банан – это ягода
Банан – это ягода, а не фрукт или овощ, как думают многие. В этой статье мы рассмотрим ряд факторов, которые позволяют считать этот плод именно ягодой. …
…
14 09 2022 22:52:22
Суррогатное материнство — что это и как происходит
С начала 21 века наука сделала огромный прорыв во всех сферах знания. Медицина, естественно, также стремительно развивается. В связи с этим возникло такое…
13 09 2022 16:38:41
20 интересных фактов о Польше
Интересные факты о Польше – это прекрасная возможность узнать больше о Центральной Европе. Это унитарное государство подразделяется на 16 воеводств. В…
12 09 2022 14:16:44
15 интересных фактов о Евровидении
Интересные факты о Евровидении – это отличная возможность узнать больше о международных фестивалях. В нем принимают участие певцы и певицы из разных стран…
11 09 2022 12:54:56
5 певиц, которые похоронили свою карьеру, поссорившись с продюсерами
5 певиц, которые похоронили свою карьеру, поссорившись с продюсерами, помогут вам лучше понять важность продюсирования. В истории шоу-бизнеса известно…
В истории шоу-бизнеса известно…
10 09 2022 8:56:36
Тайны Леонардо да Винчи — интересное видео
Считается, что одним из самых гениальных людей всех времен и народов был Леонардо да Винчи. Его ум, казалось, не имел границ, а творческая способность…
09 09 2022 9:12:19
Если бы Луна была от Земли на 400 км — Интересные факты
Как вы думаете, если бы Луна была ближе к нашей планете, чем сейчас, как бы она выглядела? Но давайте обо всем по порядку. Ученые – люди странные. Порой…
08 09 2022 3:19:54
Надежда Крупская — биография, факты, фото
Надежда Крупская – русская революционерка, государственный и культурный деятель, доктор педагогических наук, основной идеолог советского образования и…
07 09 2022 18:14:43
19 интересных фактов о Лихтенштейне
Интересные факты о Лихтенштейне – это прекрасная возможность узнать больше о карликовых государствах. По своим размерам Лихтенштейн скорее напоминает…
По своим размерам Лихтенштейн скорее напоминает…
06 09 2022 0:35:25
14 интересных фактов о Фонвизине
Интересные факты о Фонвизине – это замечательная возможность узнать больше о творчестве русского писателя. Его считают родоначальником русской бытовой…
05 09 2022 7:21:14
Что такое FAQ и ЧАВО — значение и примеры
Что такое FAQ и ЧАВО? Подобные термины сегодня часто встречаются на различных интернет-форумах, в чатах или в комментариях. Но что следует понимать под…
04 09 2022 3:50:58
Лев и Газель — мудрая притча для всех
Каждое утро в Африке просыпается газель. Она сразу же начинает торопиться и бежать. Она прекрасно знает, что должна бегать быстрее всех хищников, чтобы…
03 09 2022 11:41:10
Эпоха Возрождения (Ренессанса) – Интересные факты
Эпоха Возрождения или Ренессанса (от фр. Renaissance) представляет собой период европейской истории, ознаменованный многими культурными преобразованиями.
02 09 2022 11:19:50
16 интересных фактов о Хабаровске
Интересные факты о Хабаровске – это блестящая возможность узнать больше о Дальнем Востоке России. Речь пойдет о географических особенностях данного…
01 09 2022 9:45:57
Нельсон Maндела — биография, факты, фото
Нельсон Maндела – южноафриканский государственный, общественный и политический деятель. Непримиримый борец за права человека во время существования…
31 08 2022 16:33:49
Жизнь прекрасна или несколько советов от Чехова
Перед вами литературный шедевр Антона Чехова. Прочитав его, вы поймете, что жизнь действительно прекрасна, и при желании всегда можно найти, чему…
30 08 2022 8:18:36
Лучшие фото Леонида Брежнева
В данном посте мы собрали фото Леонида Брежнева в хорошем качестве. Подробнее об этом политическом деятеле Советского Союза мы писали в биографии.
29 08 2022 17:25:27
Интересные факты о морях и океанах
Каждый школьник знает, что ни один живой организм не может обойтись без воды. Планета Земля на 70% покрыта водой, и именно поэтому ее природа столь…
28 08 2022 7:20:46
Современные ценности — Интересное видео
Что такое современные ценности? Толерантность, терпимость вседозволенность или беспредел? Куда катится наш мир, и можно ли поставить знак равенства,…
27 08 2022 2:16:46
18 интересных фактов об Андерсене
Интересные факты об Андерсене – это отличная возможность узнать больше о творчестве датского писателя. Его перу принадлежат сотни произведений, которые…
26 08 2022 20:44:32
Самые красивые мужчины — ТОП 25
Содержание ТОП самых красивых мужчин Самые красивые мужчины России Самые красивые мужчины прошлого века На протяжении всей истории люди ценили красоту и. ..
..
25 08 2022 16:50:48
Мэрилин Монро — биография, личная жизнь, фото
Мэрилин Монро – американская киноактриса, ceкc-символ 1950-х годов, певица и модель. Стала одним из наиболее культовых образов американского кинематографа…
24 08 2022 21:22:58
14 интересных фактов об Иваново
Интересные факты об Иваново – это замечательная возможность узнать больше о городах России. В народе его часто называют «городом невест». В Иваново…
23 08 2022 13:26:48
Психосоматика заболеваний: 10 примеров
Знаете ли вы, что такое психосоматика? Это сложное слово состоит из двух простых древнегреческих слов: психея – душа, и сома – тело. Другими словами,…
22 08 2022 19:32:58
Татаро-монгольское иго – краткая история
Татаро-монгольским игом называют систему политической зависимости русских княжеств от Монгольской империи. В 2013 году в учебниках по истории России…
В 2013 году в учебниках по истории России…
21 08 2022 0:49:50
23 интересных факта о березах
Интересные факты о березах – это замечательная возможность узнать больше о лиственных породах деревьев. Различные части березы активно используются в…
20 08 2022 9:58:26
17 интересных фактов об осьминогах
Интересные факты об осьминогах – это прекрасная возможность узнать больше о моллюсках. Осьминоги встречаются во всех тропических и субтропических морях и…
19 08 2022 18:43:47
Энтони Джошуа — биография, факты, фото
Энтони Джошуа (р. 1989) – британский профессиональный боксер, выступающий в тяжелой весовой категории. Олимпийский чемпион 30-х Олимпийских игр-2012 в…
18 08 2022 1:18:15
14 интересных фактов о гусях
Интересные факты о гусях – это прекрасная возможность узнать больше о птицах семейства утиных. На протяжении долгого времени их активно разводят в самых…
На протяжении долгого времени их активно разводят в самых…
17 08 2022 12:10:55
Гульнара Каримова — биография, семья, фото
Гульнара Каримова – певица, дизайнер, дипломат и предприниматель. Старшая дочь первого президента Узбекистана Ислама Каримова. В период 2010-2012 гг….
16 08 2022 20:19:10
Продукты для мозга — Еда и мозг
Продукты для мозга, которые мы рассмотрим в данной статье, способствуют улучшению умственной деятельности. Исследования показывают, что наш мозг…
15 08 2022 19:27:44
Признаки беременности на ранних сроках
Каждая дeвyшка мечтает родить и воспитать ребенка. Однако при первом зачатии многие не знают, каким образом на ранних сроках можно распознать…
14 08 2022 15:47:16
17 интересных фактов о Ереване
Интересные факты о Ереване – это замечательная возможность узнать больше о европейских столицах. Ереван является политическим, экономическим, культурным и…
Ереван является политическим, экономическим, культурным и…
13 08 2022 0:38:16
13 интересных фактов о физике
Интересные факты о физике – это блестящая возможность узнать больше нового из мира науки. Физика является естественной наукой, изучающей общие свойства…
12 08 2022 21:52:45
14 интересных фактов о водопадах
Интересные факты о водопадах – это замечательная возможность узнать больше о природных явлениях. Крупные водопады поражают своей мощью и красотой. Вокруг…
11 08 2022 17:44:25
16 интересных фактов про Юрия Гагарина
Интересные факты про Юрия Гагарина – это прекрасная возможность узнать больше о самом известном в мире космонавте. Имя этого человека золотыми буквами…
10 08 2022 5:18:43
Всё хорошо, прекрасная маркиза — Значение и происхождение
Крылатое выражение «Всё хорошо, прекрасная маркиза» известно многим. Однако о его происхождении догадываются не все. Чтобы наиболее уместно использовать…
Однако о его происхождении догадываются не все. Чтобы наиболее уместно использовать…
09 08 2022 23:43:43
Импринтинг — Значение и примеры
В психологии существует один интересный термин, который называется «импринтинг». В буквальном смысле это понятие переводится как «запечатлеть», «оставить…
08 08 2022 15:11:33
Иван Федоров — биография, личная жизнь, фото
Иван Федоров (также Федорович, Москвитин) – один из первых российских книгопечатников. Как правило, его называют «первым русским книгопечатником» по…
07 08 2022 7:24:54
Наталья Водянова — биография, факты, фото
Наталья Михайловна Водянова – российская супермодель, актриса и филантроп. Является официальным лицом нескольких престижных модных домов. В биографии…
06 08 2022 7:18:58
Полина Гриффис — биография, факты, фото
Полина Гриффис – российская певица, экс-солистка группы «А-Студио» (2001-2004). Сотрудничала с датским исполнителем Томасом Н’эвергрином. Она продолжает…
Сотрудничала с датским исполнителем Томасом Н’эвергрином. Она продолжает…
05 08 2022 8:13:11
Интересные факты о крови
Интересные факты о крови человека многим не известны. А ведь эта драгоценная жидкость обеспечивает жизнедеятельность нашего организма! За сутки сердце…
04 08 2022 21:17:20
Паритет покупательной способности
Читаю статью о том, что такое ВВП, вы могли заинтересоваться таким понятием, как паритет покупательной способности (ППС). Несложно догадаться, что наука…
03 08 2022 13:48:54
10 распространенных когнитивных искажений
Перед вами подборка из 10 распространенных когнитивных искажений. Более подробно о том, что собой представляют когнитивные искажения, и как они влияют на…
02 08 2022 0:42:15
Семь чудес света: Статуя Зевса в Олимпии
Олимпийские игры, которым столь много внимания уделяли греки, проводились, как правило, в честь языческого бога Зевса. Однако храма этого мифического персонажа не существовало! Лишь в 466-465 годах в Олимпии было построено уникальное здание, в котором через время появилась грандиозная статуя Зевса….
Однако храма этого мифического персонажа не существовало! Лишь в 466-465 годах в Олимпии было построено уникальное здание, в котором через время появилась грандиозная статуя Зевса….
01 08 2022 16:50:22
Иоганн Гете — биография, личная жизнь, фото
Иоганн Гете – выдающийся немецкий писатель, поэт, мыслитель, философ и естествоиспытатель, государственный деятель. Произведения Гете, в особенности…
31 07 2022 11:24:10
Еще:
Полезная информация -1 :: Полезная информация -2 :: Полезная информация -3 :: Полезная информация -4 :: Полезная информация -5 :: Полезная информация -6 :: Полезная информация -7 :: Полезная информация -8 :: Полезная информация -9 ::
Полезные факты для решения задач по геометрии
Анна Малкова
Полезные факты для решения задач ЕГЭ по геометрии (ЕГЭ по математике, Часть 2, профильный уровень).
Как научиться решать задачи ЕГЭ по геометрии (задача 16, Профильный уровень)?
Школьные учебники геометрии (Л. С. Атанасян, А. Г. Мерзляк…) неплохие. Даже лучше, чем по алгебре. Однако в них нет задач из вариантов ЕГЭ. Непонятно, как по ним готовиться к ЕГЭ, на что обращать внимание. Да и нет времени в 11-м классе заново читать учебник и решать все задачи подряд.
С. Атанасян, А. Г. Мерзляк…) неплохие. Даже лучше, чем по алгебре. Однако в них нет задач из вариантов ЕГЭ. Непонятно, как по ним готовиться к ЕГЭ, на что обращать внимание. Да и нет времени в 11-м классе заново читать учебник и решать все задачи подряд.
В освоении планиметрии важен правильный подход. Многие начинают с реальных задач ЕГЭ, а когда не получается, чувствуют разочарование. Не стоит так делать.
Первый этап: выучите теорию. Определения, теоремы, признаки. Основные формулы. Например, для площади треугольника нам нужны 5 формул. Помните их? Все они применяются в решении задач. Теоремы синусов и косинусов. Свойства высот, медиан и биссектрис. И многое другое.
В этом вам поможет Полный справочник Анны Малковой для подготовки к ЕГЭ по математике. Именно то, что нужно для решения задач ЕГЭ. Ничего лишнего. А цветные картинки запоминаются сами собой.
И конечно, практика! Решаем задачи ЕГЭ. Сначала – Часть 1, задачи 3 и 6. Не меньше 50 задач первой части ЕГЭ по теме «Планиметрия» надо решить, чтобы выучить и уметь применять теоремы и формулы планиметрии.
Изучить планиметрию и потренироваться в решении задач можно на нашем Онлайн-курсе.
Задачи, решения, видеоразбор.
Отлично, освоили задачи по планиметрии 1 части Профильного ЕГЭ по математике. Пора переходить ко второй! К задаче 16. Но не будем спешить. Пункт (а) задачи 16 Профильного ЕГЭ по математике – доказательство. А вы знаете, что пункт (а) нужен не только для того, чтобы вы получили один из трех баллов за эту задачу? Что во многих задачах ЕГЭ №16 пункт (а) содержит идеи для решения пункта (б). Намеки на то, как решить задачу полностью. Надо научиться доказывать всевозможные утверждения планиметрии.
Мы публикуем для вас новый и ценный материал — доказательство полезных фактов. Это и повторение всего курса (7-9 класс), и «заготовки» для многих задач ЕГЭ.
Приведем список из 32 полезных фактов. Докажите их самостоятельно и проверьте решения по ссылкам.
Для большинства этих полезных фактов приведены примеры решения задач и первой, и второй части Профильного ЕГЭ по математике.
Углы, треугольники, четырехугольники
1. Биссектрисы смежных углов перпендикулярны.
2. Свойство медианы прямоугольного треугольника.
3. Сумма квадратов диагоналей параллелограмма.
4. Площадь выпуклого четырехугольника
5. Свойства трапеции: отрезок, соединяющий середины диагоналей
6. Свойства равнобедренной трапеции
7. Замечательное свойство трапеции.
8. Свойство серединных перпендикуляров к сторонам треугольника.
9. Свойства биссектрис треугольника.
10. Свойства медиан треугольника
11. Свойство высот треугольника.
Окружности
12. Диаметр, перпендикулярный хорде, делит ее пополам.
13. Теорема о пересекающихся хордах.
14. Теорема о серединном перпендикуляре к хорде.
15. Равные хорды удалены от центра окружности на равные расстояния.
16. Дуги окружности, заключенные между параллельными хордами, равны.
17. Угол между касательной и хордой.
18. Теорема о секущей и касательной.
Теорема о секущей и касательной.
19. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
20. Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности.
21. Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен .
22. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
23. Если расстояние между центрами окружностей радиусами R и r равно а и , то отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и
24. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов.
25. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
26. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии.
27. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то АМ = р – ВС, где р – полупериметр треугольника АВС.
28. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
29. Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен , то угол KLM .
30. Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника АВС лежит на окружности S.
31. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна .
32. Свойство биссектрисы треугольника. Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.
*При составлении списка полезных фактов использованы учебные пособия Р. К. Гордина.
Интересное о геометрии.
 «Школьная газета » Интересные факты о геометрии»
«Школьная газета » Интересные факты о геометрии»Содержание
- Интересное о геометрии. «Школьная газета » Интересные факты о геометрии»
- Интересные факты о треугольниках в геометрии. Интересные факты о геометрии
- Интересные факты о углах. Интересные факты об угле
- Интересные факты о конусе. Конусы
- История развития геометрии Интересные факты. История развития геометрии
Интересное о геометрии. «Школьная газета » Интересные факты о геометрии»
Интересные факты о геометрии.Слово «трапеция» произошло от древнегреческого слова «трапезион»(обозначает столик). также от данного слова произошли уже немногоподзабытые в обиходе слова, такие как «трапеза» и прочие родственныеему слова.Математика для древних греков была, прежде всего, геометрией.Поэтому над двери Академии, в стенах которой Платон учил своих учеников, висела надпись: «Пусть сюда не входит тот, кто не знает геометрии».Греческое слово «конос», обозначающее сосновую шишку, является словарной основой для такого термина как «конус», а известный в геометрии термин «линия» возник уже от латинского слова «линум» (что в переводе на русский язык означает «льняная нить»). Пирог разрезается всего тремя касаниями ножа на восемь равных долей. Причем, существует только два способа это сделать. Под треугольником Рёло понимают геометрическую фигуру, образованную пересечением 3 кругов одинакового радиуса D с центрами, находящимися в вершинах равностороннего треугольника, такой же по длине стороны. на основе треугольника Рёло было придумано сверло, позволяющее просверливатьпочти квадратные отверстия. В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180. В геометрии Римана сумма углов треугольника всегда больше 180.Если число 111 111 111 помножить на себя самого, то получится интересное число 12 345 678 987 654 321 (все числа сначала возрастают, а потом убывают по порядку).Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года.
Пирог разрезается всего тремя касаниями ножа на восемь равных долей. Причем, существует только два способа это сделать. Под треугольником Рёло понимают геометрическую фигуру, образованную пересечением 3 кругов одинакового радиуса D с центрами, находящимися в вершинах равностороннего треугольника, такой же по длине стороны. на основе треугольника Рёло было придумано сверло, позволяющее просверливатьпочти квадратные отверстия. В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180. В геометрии Римана сумма углов треугольника всегда больше 180.Если число 111 111 111 помножить на себя самого, то получится интересное число 12 345 678 987 654 321 (все числа сначала возрастают, а потом убывают по порядку).Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.Еще факты Знаете ли вы? Что Шарль Перро, автор «Красной Шапочки», написал сказку «Любовь циркуля и линейки»? Что Наполеон Бонапарт писал математические труды и один геометрический факт называется «Задача Наполеона»? Что Пифагор был победителем из кулачного боя на 58-х Олимпийских играх, проходивших в 548 году до н. э., а затем побеждал еще на нескольких Олимпиадах? Выполнил Меркулов Лев,Педагог Меркулова О.Р.
В этот день он и умер.Еще факты Знаете ли вы? Что Шарль Перро, автор «Красной Шапочки», написал сказку «Любовь циркуля и линейки»? Что Наполеон Бонапарт писал математические труды и один геометрический факт называется «Задача Наполеона»? Что Пифагор был победителем из кулачного боя на 58-х Олимпийских играх, проходивших в 548 году до н. э., а затем побеждал еще на нескольких Олимпиадах? Выполнил Меркулов Лев,Педагог Меркулова О.Р.
Интересные факты о треугольниках в геометрии. Интересные факты о геометрии
- Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
- Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
- С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
- Одна из известных геометрических задач называется «задача Наполеона».
 Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ). - Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
- Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
- В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
- Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
- Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).

- Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
- Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
- Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
- Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
- При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
- Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

Интересные факты о углах. Интересные факты об угле
Человек использует уголь в качестве топлива с древнейших времен. С момента изобретения его использовали для самых разных целей. Это было и приготовление еды, и промышленное производство. Благодаря углю стало возможно изготавливать сталь. С углем связано множество интересных фактов, а его роль в нашей жизни колоссальна.
Образование угля в недрах земли – очень долгий процесс. Здесь много общего с нефтью. Уголь образуется из погибших растений, которые по тем или иным причинам оказывались под землей. Здесь без кислорода они не гнили, и их остатки не теряли содержавшийся в них углерод – основу угля. Далее в течение миллионов лет под воздействием самых разных факторов эти остатки превращались в торф, а из него в уголь. А дальнейший процесс приводит к образованию графита.Прежде, чем углубляться в интересные факты о технология добычи и интересных ситуаций, связанных с углем, поговорим об углях, необходимых для приготовления пищи:Вообще основное отличие японской кухни от европейской – доминирование морепродуктов. Их используют повсеместно. И даже для шашлыков, которые японцы называют «тэмпора». Правда, при этом они не очень часто используют уголь для их приготовления. Считается, что он способен впитывать запахи и затем отдавать их готовящемуся блюду. Углю в основном предпочитают открытый огонь. А в дополнение часто используют имбирь, который также устраняет запахи.
Их используют повсеместно. И даже для шашлыков, которые японцы называют «тэмпора». Правда, при этом они не очень часто используют уголь для их приготовления. Считается, что он способен впитывать запахи и затем отдавать их готовящемуся блюду. Углю в основном предпочитают открытый огонь. А в дополнение часто используют имбирь, который также устраняет запахи.
В Северной Африке во франкоговорящих странах любят использовать сухой кустарники и прочие мелкие растения. Здесь пустыня, и крупных деревьев нет. Угли делают, например, из саксаула. Они получаются горячими и обладающими специфическим ароматом.
У нас же в России привычнее использовать уголь для шашлыка в брикетах. Лично от себя могу посоветовать компанию «Добрый уголь», которая специализирутеся на производстве угля для кальяна и барбекю наивысшего качества.
Шахты, в которых добывают уголь, являются довольно опасным местом. В них выделяются различные газы. Особо опасен метан. Он вытесняет часть кислорода и делает воздух взрывоопасным. Раньше, когда индикаторов метана не существовало, использовали канареек. Их брали с собой в шахту, и если птицам становилось плохо, это означало, что в шахте скопился метан.
Раньше, когда индикаторов метана не существовало, использовали канареек. Их брали с собой в шахту, и если птицам становилось плохо, это означало, что в шахте скопился метан.
Среди других опасностей выделяются пожары в шахтах. Как в случаях с горящим торфом, они могут длить достаточно долго. Рекордным получился пожар на месторождении Люхуангоу в Китае. На его устранение ушло целых 130 лет, и окончательно его потушили только в 2004 году. Было уничтожено около 260 млн. тонн угля.
С углем и его месторождениями связано множество забавных ситуаций. В нем часто находили сокровища. Так в 1891 году повезло некой госпоже Калп, нашедшей в большом куске угля старинную золотую цепочку. Уголь хранит множество древних артефактов. Шахтеры не раз находили останки древних сооружений. Как, например, в американском городке Хаммондвилле, где в 1869 году нашли останки стены с иероглифами.
Уголь продолжает играть большую роль в жизни людей и даже целых городов. Интересно проследить судьбу японского города Хасима, находящегося на одноименном острове, который был некогда богат углем. Начиная с 30-х годов века прошлого, этот город долгое время считался самым густонаселенным в мире. Остров обладал береговой линией всего в 1 км, но его население составляло более 5 тыс. человек. Но к середине 70-х уголь здесь закончился. Люди начали покидать это место. Город стал абсолютно заброшенным. Сейчас там даже проводят экстремальные экскурсии.
Начиная с 30-х годов века прошлого, этот город долгое время считался самым густонаселенным в мире. Остров обладал береговой линией всего в 1 км, но его население составляло более 5 тыс. человек. Но к середине 70-х уголь здесь закончился. Люди начали покидать это место. Город стал абсолютно заброшенным. Сейчас там даже проводят экстремальные экскурсии.
В России находятся огромные запасы угля. Ученые заявляют о 4 триллионах тонн запасов. Это чуть менее трети от общемировых.
Уголь может иметь не только привычную твердую форму. Сегодня имеются технологии, превращающие его в жидкое топливо, очень похожее на нефть.
В промышленности уголь используют не только в качестве топлива. Он является сырьем для производства различных материалов. Например, из каменного угля делают искусственный графит. А еще из угля добывают содержащиеся в нем полезные материалы: свинец, серу, галлий, цинк и другие.
Источник: https://interesnyefakty.com/novosti/geometriya-fakty-interesnye-interesnye-fakty-o-geometrii
Интересные факты о конусе.
 Конусы
КонусыБрюхоногие моллюски рода конус обладают раковиной, длина которой 15 20 см, а форма напоминает коническую. Раковины этих животных окрашены в красивые тона и имеют на поверхности изысканный узор, чем и привлекают коллекционеров, стремящихся заполучить такую раковину. Эти раковины привлекают внимание и охотников за моллюсками, так как на рынках они высоко ценятся туристами.
K наиболее распространенным и брюхоногих моллюсков рода конус относятся:
- , живущие в зоне от Полинезии до Индийского океана;
- , обитающий в зоне Полинезии, и вплоть, до восточного побережья Африки;
- обитающие в регионе от Красного моря до Полинезии;
- — житель берегов Австралии и восточного побережья Африки.
Ловцы конусов могут получить уколы от этих животных, когда они складывают моллюсков в сетчатые мешки, а также могут пострадать и при неосторожной транспортировке мешка, который они, как правило, привязывают к поясу. Сказанное относится к ловцам-профессионалам. Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.
Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.
Готовясь напасть , моллюск выдвигает зубы в переднюю часть головы, чтобы вонзить их в тело жертвы. К зубам подходит яд из канала радулы и глотки. В хоботке расположен один из зубов радулы. При уколе пузырек сжимается и яд под давлением вгоняется в свернутые, похожие на острый полый гарпун — зубы радулы.
Конусы обычно предпочитают держаться или свободно . Тропические виды этих моллюсков представляют реальную угрозу для человека, так как их яд, попавший в организм, часто вызывает гибель пострадавших. Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.
Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.
Б. Холстед считает, что при развивающихся симптомах отравления ядом расстройства дыхания обычно не бывает, а В. Н. Орлова и Д. Б. Гелашвили указывают, что в тяжелых случаях человек погибает не от остановки сердца, а от паралича дыхательной мускулатуры.
Для предупреждения поражений этими моллюсками можно порекомендовать единственный способ, а именно, быть крайне аккуратным при прикосновении к раковинам неизвестных моллюсков. Брать их необходимо очень осторожно, избегая мягких тканей животного.
История развития геометрии Интересные факты. История развития геометрии
Самые первые понятия в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков. Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».
Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков. Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».
Греческие ученые на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.
С этого источника также начинается и история развития математики.
Однако в труде Евклида ничего не сказано ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру (хотя присутствует теорема о площади круга). История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду, который смог вычислит число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость.
Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний во II веке до нашей эры сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.
Аполлоний во II веке до нашей эры сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.
Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Однако в дальнейшем история развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.
На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.
Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.
Источник: https://interesnyefakty.com/novosti/interesnye-fakty-geometriya-interesnye-fakty-o-geometrii
Интересные факты о Евклиде | VivaReit
Античный математик и философ Евклид жил в 3 веке до нашей эры. И математиком он был действительно выдающимся – не только для своего времени, но и для современности. Ведь та самая геометрия, которую сегодня изучают школьники всего мира, носит название евклидовой. Она базируется на пяти аксиомах, выведенных именно им. Без преувеличения, этот ученый заложил фундамент современной геометрии и во многом – математики как науки.
Без преувеличения, этот ученый заложил фундамент современной геометрии и во многом – математики как науки.
И наверняка многим будет интересно узнать некоторые занимательные факты из жизни Евклида.
Откуда и когда
Примечательно, что доподлинно не известно, когда именно и в каком месте родился Евклид. По скудным записям из арабских книг 12-го века можно судить, что отца его звали Наукрат, а сам будущий великий математик родился в Греции.
Предполагается, что свое образование он начал получать Академии Платона, при входе в которую, кстати, была надпись: «Никогда не войдет сюда тот, кто не знает геометрии».
Впрочем, и обстоятельства и даже точная дата смерти Евклида также покрыты тайной: предполагается, что это печальное событие произошло не позднее 265 года до нашей эры.
Царские пути
Одна из самых известных легенд о Евклиде дошла до нас со слов самого Архимеда. Тот поведал, что однажды сам царь Птолемей решил начать изучать геометрию по «Началам» Евклида. Однако наука показалась царской особе весьма трудной и никак не давалась. И тогда Птолемей поинтересовался, нет ли способа как-нибудь попроще и побыстрее все освоить… На что Евклид произнес сегодня уже ставшую крылатой фразу: «В геометрии нет царских путей».
Однако наука показалась царской особе весьма трудной и никак не давалась. И тогда Птолемей поинтересовался, нет ли способа как-нибудь попроще и побыстрее все освоить… На что Евклид произнес сегодня уже ставшую крылатой фразу: «В геометрии нет царских путей».
Выгодная наука
Также известен случай, когда один ученик поинтересовался у знаменитого математика, чем ему может оказаться выгодной геометрия в жизни. На что Евклид подозвал слугу и велел дать ученику три обола (денежная единица), сказав при этом:
— Дай ему денег, раз ему хочется только прибыли от науки.
Множество Начал
Интересно, что «Начала» Евклида не были единственными «Началами» и до него. Прежде многие ученые писали научные труды, и носили они название именно «Начала». Однако только Евклидовы стали знамениты в веках.
Но великий геометр не строил свои труда на абсолютно пустом месте. Справедливости ради, стоит отметить, что многие из его теорем строились на базе уже имевшихся в то время знаний. Но Евклид собрал их воедино, классифицировал и смог обосновать с научной точки зрения.
Но Евклид собрал их воедино, классифицировал и смог обосновать с научной точки зрения.
По строгой логической цепочке
Именно в своих «Началах» Евклид сделал то, что сегодня кажется само собой разумеющимся: он стал основывать все свои выводы на цепочке строгих логических выводов. При этом он считал важным, что цепочка должна где-то начинаться, а не вырастать из пустого места, поскольку при этом она может никогда и не закончиться. Должно быть, с этим связано и само название его научного труда. Но, поскольку добраться до самого начального суждения было весьма трудно, Евклид сам сформулировал свои знаменитые аксиомы – утверждения, не требующие доказательств. И только на этих аксиомах ему удалось вывести все остальные доказательства и теоремы.
Платон мне друг
Как уже было сказано, Евклид обучался в школе у самого Платона. Не удивительно, что и по философским своим суждениям он относился к так называемым платоником. В частности, он полагал, что в основе всего лежат четыре элемента – вода, воздух, земля и огонь.

Недоказанные труды Евклида
Арабы – да и не только они – часто приписывают Евклиду и прочие труды во многих областях знаний, начиная от музыки и заканчивая медициной. Например, фундаментальный труд по теории музыки «Гармоника», а также «Деление канонов». Однако уже в наше время было доказано, что никакого отношения математик к данным трудам не имеет. Скорее всего, автором их был пифагореец Клеонид. Хотя и это доподлинно не известно.
Добрая математика
Другой древний математик – Папп – сообщает, что Евклид был необычайно мягок и добр по отношению к тем, кто, во-первых, мог бы помочь в распространении математики как науки, а во-вторых, если видел, что человек действительно испытывает тягу к геометрии. Он был способен даже изменить свое мнение о том или ином человеке, если вдруг узнавал, что того интересует или наоборот – не интересует – математика.
И музей, и библиотека
Также известно, что Евклид на рубеже третьего столетия до нашей эры организовывал открытие музея и библиотеки в городе Александрии. Здесь же он совершил впоследствии множество своих открытий. Кроме того, и музей, и библиотека при Евклиде играли роль древних научных центров.
Здесь же он совершил впоследствии множество своих открытий. Кроме того, и музей, и библиотека при Евклиде играли роль древних научных центров.
«Вечная» книга
Подчиняясь школе Платона, Евклид полагал, что все, что он излагает в своих «Началах» не только не подвергается сомнению, но и будет существовать вечно. Как бы то ни было, но более 2 тысяч лет именно по трудам Евклида ученики осваивают премудрости геометрии.
Неевклидова геометрия
И только через 2 с лишним тысячи лет российский математик Лобачевский усомнился в безраздельной справедливости геометрии Евклида. Он вывел «свою собственную» геометрию, которая базировалась не на плоскости, а на псевдосфере. Интересно, что все Аксиомы, выведенные Евклидом, сохранялись. Кроме одной – о параллельных прямых.
Кроме Лобачевского, «свою» геометрию вывел и немецкий математик Риман. В настоящее время три геометрии странным образом сосуществуют в мире – Евклидова, Римана и Лобачевского.
Так ли это было, как описывают некоторые истории о Евклиде, а, может, и вовсе ничего подобного не было – не столь уж важно. \circ\).
\circ\).
Вертикальные углы равны: \(\alpha=\gamma\).
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. \circ\).
\circ\).
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
\[{\Large{\text{Параллельные прямые}}}\]
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной. \circ\), то \(\angle 4 = \angle 1 + \angle 2\), что и требовалось доказать.
\circ\), то \(\angle 4 = \angle 1 + \angle 2\), что и требовалось доказать.
\[{\Large{\text{Равнобедренный треугольник}}}\]
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть \(ABC\) – равнобедренный треугольник, \(AB = BC\), \(BD\) – биссектриса (проведённая к основанию).
Рассмотрим треугольники \(ABD\) и \(BCD\): \(AB = BC\), \(\angle ABD = \angle CBD\), \(BD\) – общая. Таким образом, \(\triangle ABD = \triangle BCD\) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что \(AD = DC\), следовательно, \(BD\) – медиана. \circ = \angle CDB\), то есть \(BD\) – высота.
\circ = \angle CDB\), то есть \(BD\) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису \(BD\) (см. рисунок из предыдущей теоремы). Тогда \(\triangle ABD=\triangle CBD\) по первому признаку, следовательно, \(\angle A=\angle C\).
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол. \circ\).
\circ\).
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
Стр 1 из 3Следующая ⇒ Полезные факты для решения задач ЕГЭ по геометрии (ЕГЭ по математике, Часть 2, профильный уровень). Как научиться решать задачи ЕГЭ по геометрии (задача 16, Профильный уровень)? Первый этап: выучите теорию. Определения, теоремы, признаки. Основные формулы. Например, для площади треугольника нам нужны 5 формул. Все они применяются в решении задач. Теоремы синусов и косинусов. Свойства высот, медиан и биссектрис. И многое другое. И конечно, практика! Решаем задачи ЕГЭ. Сначала – Часть 1, задачи 3 и 6. Не меньше 50 задач первой части ЕГЭ по теме «Планиметрия» надо решить, чтобы выучить и уметь применять теоремы и формулы планиметрии. Углы, треугольники, четырехугольники 1. 2. Пусть и – смежные углы, – биссектриса угла , – биссектриса угла . Докажем, что . 3. 4. Смежные углы – это углы, имеющие общую сторону, и их сумма равна . Так как углы и – смежные, . 5. , 6. 7. 8. . 9. Значит, , что и требовалось доказать. 10. Легко доказать также, что биссектрисы односторонних углов при параллельных прямых и секущей – перпендикулярны. Сделайте это самостоятельно. 11. Полезные следствия, применяемые в решении задач ЕГЭ: 12. Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны. 13. Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны. 14. Задача ЕГЭ по теме «Биссектрисы односторонних углов» 15. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах. 16. Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны.
2. Свойство медианы прямоугольного треугольника. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Пусть СМ — медиана прямоугольного треугольника АВС с прямым углом С. Мы получили прямоугольник АКВС (параллелограмм, в котором угол С – прямой). Задача ЕГЭ по теме «Медиана прямоугольного треугольника» Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD – равнобедренный, CD = BD. . Углы ACD и DCB в сумме дают . Отсюда .
3. Сумма квадратов диагоналей параллелограмма. Свойства равнобедренной трапеции Свойство высот треугольника Анна Малкова Окружности 12. Диаметр, перпендикулярный хорде, делит ее пополам. 13. Теорема о пересекающихся хордах. 14. Теорема о серединном перпендикуляре к хорде. 15. Равные хорды удалены от центра окружности на равные расстояния. 16. Дуги окружности, заключенные между параллельными хордами, равны. 17. Угол между касательной и хордой. 18. Теорема о секущей и касательной. 19. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами. 20. Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности. 21. Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен . 22. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним. 23. Если расстояние между центрами окружностей радиусами R и r равно а и , то отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и 24. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов. 25. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. 26. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии. 27. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то АМ = р – ВС, где р – полупериметр треугольника АВС. 28. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС. 29. Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен , то угол KLM . 30. Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника АВС лежит на окружности S. 31. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна . 32. Свойство биссектрисы треугольника. Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.
Полезные факты для решения задач ЕГЭ по геометрии (ЕГЭ по математике, Часть 2, профильный уровень). 123Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Факты о геометрии для детей
Уроки геометрии в 20 веке
Геометрия — это разновидность математики, изучающая размер, форму и положение вещей. В геометрии есть плоские (2D) формы и твердые (3D) формы. Квадраты, круги и треугольники — одни из самых простых фигур в плоской геометрии. Кубы, цилиндры, конусы и сферы — простые фигуры в объемной геометрии.
Содержание
- Применение
- Происхождение
- Примеры
- Важные понятия геометрии
- Аксиомы
- Очки
- строк
- Самолеты
- Уголки
- Кривые
- Поверхности
- Коллекторы
- Топологии и метрики
- Конструкции компаса и линейки
- Размер
- Симметрия
- Неевклидова геометрия
- Связанные страницы
- Картинки для детей
Использование
Геометрия может использоваться для измерения площади и периметра плоской формы. Его также можно использовать для измерения объема и площади поверхности твердого тела.
Его также можно использовать для измерения объема и площади поверхности твердого тела.
Геометрия может быть использована для расчета размера и формы многих вещей. Например, геометрия может помочь людям найти:
- площадь дома, чтобы они могли купить нужное количество краски
- объем коробки, чтобы узнать, достаточно ли она велика, чтобы вместить литр еды
- площадь фермы, поэтому ее можно разделить на равные части
- расстояние по краю пруда, чтобы знать, сколько ограждения купить.
Происхождение
Геометрия зародилась как искусство измерения формы земли, чтобы ее можно было справедливо разделить между людьми. Слово «геометрия» означает «измерять землю». Из этого она выросла и стала одной из важнейших частей математики. Греческий математик Евклид написал первую книгу по геометрии. Геометрия — один из древнейших разделов математики.
Примеры
Геометрия начинается с нескольких простых идей, которые считаются истинными и называются аксиомами. Например:
Например:
- Точку изображают на бумаге, касаясь ее карандашом или ручкой без каких-либо боковых движений. Мы знаем, где находится точка, но она не имеет размера.
- Прямая линия — это кратчайшее расстояние между двумя точками. Например, Софи тянет веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.
- Плоскость — это плоская поверхность, которая не останавливается ни в каком направлении. Например, представьте себе стену, бесконечно простирающуюся во всех направлениях.
Важные понятия геометрии
Ниже приведены некоторые из наиболее важных понятий геометрии.
Аксиомы
Иллюстрация постулата параллельности Евклида
- См. Также: Евклидова геометрия
Евклид использовал абстрактный подход к геометрии в своих «Элементах», одной из самых влиятельных когда-либо написанных книг. Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Точки
Главная страница: Точка (геометрия)
Точки считаются фундаментальными объектами в евклидовой геометрии. Они были определены различными способами, включая определение Евклида как «то, что не имеет частей», а также с помощью алгебры или вложенных множеств. Во многих областях геометрии, таких как аналитическая геометрия, дифференциальная геометрия и топология, все объекты считаются построенными из точек. Однако некоторые исследования геометрии проводились без привязки к точкам.
Однако некоторые исследования геометрии проводились без привязки к точкам.
Линии
Главная страница: Линия (геометрия)
Евклид описал линию как «длину без ширины», которая «равномерна по отношению к точкам на самой себе». В современной математике, учитывая множество геометрий, понятие линии тесно связано со способом описания геометрии. Например, в аналитической геометрии линия на плоскости часто определяется как множество точек, координаты которых удовлетворяют заданному линейному уравнению, но в более абстрактных условиях, таких как геометрия инцидентности, линия может быть независимым объектом, отличным от множество точек, лежащих на нем. В дифференциальной геометрии геодезическая — это обобщение понятия линии на искривленные пространства.
Плоскости
Плоскость (геометрия)
Плоскость — это плоская двумерная поверхность, простирающаяся бесконечно далеко. Плоскости используются во всех областях геометрии. Например, плоскости можно изучать как топологическую поверхность без привязки к расстояниям или углам; его можно изучать как аффинное пространство, где можно изучать коллинеарность и отношения, но не расстояния; его можно изучать как комплексную плоскость с использованием методов комплексного анализа; и так далее.
Уголки
Main page: Angle
Евклид определяет плоский угол как наклон друг к другу в плоскости двух прямых, которые пересекаются и не лежат прямо относительно друг друга. Говоря современным языком, угол — это фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла.
Острый (а), тупой (б) и прямой (в) углы. Острые и тупые углы также известны как косые углы.
В евклидовой геометрии углы используются для изучения многоугольников и треугольников, а также как самостоятельный объект изучения. Изучение углов треугольника или углов единичной окружности составляет основу тригонометрии.
В дифференциальной геометрии и исчислении углы между плоскими кривыми, пространственными кривыми или поверхностями можно вычислить с помощью производной.
Кривые
Кривая — это одномерный объект, который может быть прямым (как линия) или нет; кривые в 2-мерном пространстве называются плоскими кривыми, а кривые в 3-мерном пространстве называются пространственными кривыми.
В топологии кривая определяется функцией от интервала действительных чисел до другого пространства. В дифференциальной геометрии используется то же определение, но определяющая функция должна быть дифференцируемой. Алгебраическая геометрия изучает алгебраические кривые, которые определяются как алгебраические многообразия размерности один.
Поверхности
Сфера — это поверхность, которую можно задать параметрически (посредством x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ ) or implicitly (by x 2 + y 2 + z 2 − r 2 = 0.)
Поверхность — это двумерный объект, такой как сфера или параболоид. В дифференциальной геометрии и топологии поверхности описываются двумерными «участками» (или окрестностями), которые собираются диффеоморфизмами или гомеоморфизмами соответственно. В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
Многообразия
Главная страница: Многообразие
Многообразие является обобщением понятий кривой и поверхности. В топологии многообразие — это топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную евклидову пространству. В дифференциальной геометрии дифференцируемое многообразие — это пространство, каждая окрестность которого диффеоморфна евклидову пространству.
Многообразия широко используются в физике, в том числе в общей теории относительности и теории струн
Топологии и метрики
Главная страница: Топология
Визуальная проверка теоремы Пифагора для треугольника (3, 4, 5), как в Zhoubi Suanjing 500–200 г. до н.э. Теорема Пифагора является следствием евклидовой метрики.
Топология — это математическая структура множества, которая сообщает, как элементы множества пространственно соотносятся друг с другом. Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Конструкции компаса и линейки
Главная страница: Конструкции компаса и линейки
Классические геометры уделяли особое внимание построению геометрических объектов, которые были описаны другим способом. Классически единственными инструментами, разрешенными в геометрических построениях, являются циркуль и линейка. Кроме того, каждое построение должно было быть завершено за конечное число шагов. Однако некоторые задачи оказалось трудно или невозможно решить только этими средствами, и были найдены остроумные конструкции с использованием парабол и других кривых, а также механических устройств.
Размер
Главная страница: Размер
Снежинка Коха с фрактальной размерностью = log4/log3 и топологической размерностью = 1
Там, где традиционная геометрия допускала измерения 1 (линия), 2 (плоскость) и 3 (наш окружающий мир, воспринимаемый как трехмерное пространство), математики использовали более высокие измерения в течение почти двух столетий. Измерение прошло через этапы превращения в любое натуральное число n , возможно бесконечное с введением гильбертова пространства, и в любое положительное действительное число во фрактальной геометрии. Теория размерности — это техническая область, изначально входящая в общую топологию, в которой обсуждаются определения ; как и большинство математических идей, размерность теперь определяется, а не интуиция. Связные топологические многообразия имеют четко определенную размерность; это скорее теорема (инвариантность области), чем что-либо априорное .
Вопрос размерности по-прежнему важен для геометрии, несмотря на отсутствие полных ответов на классические вопросы. Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Симметрия
Главная страница: Симметрия
Мозаика гиперболической плоскости
Тема симметрии в геометрии почти так же стара, как и сама геометрическая наука. Симметричные формы, такие как круг, правильные многоугольники и платоновые тела, имели большое значение для многих древних философов и подробно исследовались еще до Евклида. Симметричные узоры встречаются в природе и были художественно воспроизведены во множестве форм, в том числе в графике М. К. Эшера. Тем не менее, только во второй половине 19 в.века, когда была признана объединяющая роль симметрии в основаниях геометрии. Эрлангенская программа Феликса Кляйна провозгласила, что в очень точном смысле симметрия, выраженная через понятие группы преобразования, определяет, какая геометрия есть . Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Другим типом симметрии является принцип двойственности в проективной геометрии (см. Двойственность (проективная геометрия)) среди других областей. Это метафеномен можно примерно описать так: в любой теореме поменяйте точку на плоскость , соедините с и , лежит в , а содержит , и вы получите столь же истинную теорему. Аналогичная и тесно связанная форма двойственности существует между векторным пространством и его дуальным пространством.
Неевклидова геометрия
Дифференциальная геометрия использует инструменты исчисления для изучения проблем, связанных с кривизной.
За почти две тысячи лет после Евклида, в то время как круг геометрических вопросов, задаваемых и ответов, неизбежно расширялся, основное понимание пространства оставалось в основном тем же самым. Иммануил Кант утверждал, что существует только одна абсолютная геометрия, истинность которой известна априорно внутренней способностью ума: евклидова геометрия была априорно синтетической. Этот господствующий взгляд был опрокинут революционным открытием неевклидовой геометрии в работах Бойяи, Лобачевского и Гаусса (так и не опубликовавшего свою теорию). Они продемонстрировали, что обычное евклидово пространство — лишь одна из возможностей развития геометрии. Широкое видение предмета геометрии было затем выражено Риманом в его инаугурационной лекции 1867 г. Über die Hypothesen, welche der Geometrie zu Grunde liegen ( О гипотезах, на которых основана геометрия ), опубликовано только после его смерти. Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Связанные страницы
- Топология
Картинки для детей
Европейец и араб, практикующие геометрию в 15 веке
Женщина преподает геометрию . Иллюстрация в начале средневекового перевода «Начал» Евклида (ок. 1310 г.).
Утолщение узла трилистник
Quintic Калаби-Яу тройной
Медресе Бу Инания, Фес, Марокко, мозаичные плитки зеллидж, образующие сложные геометрические мозаики
Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Цитируйте эту статью:
Факты о геометрии для детей. Энциклопедия Киддла.
Энциклопедия Киддла.
Факты о геометрии для детей
Уроки геометрии в 20 веке
Геометрия — это разновидность математики, изучающая размер, форму и положение вещей. В геометрии есть плоские (2D) формы и твердые (3D) формы. Квадраты, круги и треугольники — одни из самых простых фигур в плоской геометрии. Кубы, цилиндры, конусы и сферы — простые фигуры в объемной геометрии.
Содержание
- Применение
- Происхождение
- Примеры
- Важные понятия геометрии
- Аксиомы
- Очки
- строк
- Самолеты
- Уголки
- Кривые
- Поверхности
- Коллекторы
- Топологии и метрики
- Конструкции компаса и линейки
- Размер
- Симметрия
- Неевклидова геометрия
- Связанные страницы
- Картинки для детей
Использование
Геометрия может использоваться для измерения площади и периметра плоской формы. Его также можно использовать для измерения объема и площади поверхности твердого тела.
Его также можно использовать для измерения объема и площади поверхности твердого тела.
Геометрия может быть использована для расчета размера и формы многих вещей. Например, геометрия может помочь людям найти:
- площадь дома, чтобы они могли купить нужное количество краски
- объем коробки, чтобы узнать, достаточно ли она велика, чтобы вместить литр еды
- площадь фермы, поэтому ее можно разделить на равные части
- расстояние по краю пруда, чтобы знать, сколько ограждения купить.
Происхождение
Геометрия зародилась как искусство измерения формы земли, чтобы ее можно было справедливо разделить между людьми. Слово «геометрия» означает «измерять землю». Из этого она выросла и стала одной из важнейших частей математики. Греческий математик Евклид написал первую книгу по геометрии. Геометрия — один из древнейших разделов математики.
Примеры
Геометрия начинается с нескольких простых идей, которые считаются истинными и называются аксиомами. Например:
Например:
- Точку изображают на бумаге, касаясь ее карандашом или ручкой без каких-либо боковых движений. Мы знаем, где находится точка, но она не имеет размера.
- Прямая линия — это кратчайшее расстояние между двумя точками. Например, Софи тянет веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.
- Плоскость — это плоская поверхность, которая не останавливается ни в каком направлении. Например, представьте себе стену, бесконечно простирающуюся во всех направлениях.
Важные понятия геометрии
Ниже приведены некоторые из наиболее важных понятий геометрии.
Аксиомы
Иллюстрация постулата параллельности Евклида
- См. Также: Евклидова геометрия
Евклид использовал абстрактный подход к геометрии в своих «Элементах», одной из самых влиятельных когда-либо написанных книг. Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Точки
Главная страница: Точка (геометрия)
Точки считаются фундаментальными объектами в евклидовой геометрии. Они были определены различными способами, включая определение Евклида как «то, что не имеет частей», а также с помощью алгебры или вложенных множеств. Во многих областях геометрии, таких как аналитическая геометрия, дифференциальная геометрия и топология, все объекты считаются построенными из точек. Однако некоторые исследования геометрии проводились без привязки к точкам.
Однако некоторые исследования геометрии проводились без привязки к точкам.
Линии
Главная страница: Линия (геометрия)
Евклид описал линию как «длину без ширины», которая «равномерна по отношению к точкам на самой себе». В современной математике, учитывая множество геометрий, понятие линии тесно связано со способом описания геометрии. Например, в аналитической геометрии линия на плоскости часто определяется как множество точек, координаты которых удовлетворяют заданному линейному уравнению, но в более абстрактных условиях, таких как геометрия инцидентности, линия может быть независимым объектом, отличным от множество точек, лежащих на нем. В дифференциальной геометрии геодезическая — это обобщение понятия линии на искривленные пространства.
Плоскости
Плоскость (геометрия)
Плоскость — это плоская двумерная поверхность, простирающаяся бесконечно далеко. Плоскости используются во всех областях геометрии. Например, плоскости можно изучать как топологическую поверхность без привязки к расстояниям или углам; его можно изучать как аффинное пространство, где можно изучать коллинеарность и отношения, но не расстояния; его можно изучать как комплексную плоскость с использованием методов комплексного анализа; и так далее.
Уголки
Main page: Angle
Евклид определяет плоский угол как наклон друг к другу в плоскости двух прямых, которые пересекаются и не лежат прямо относительно друг друга. Говоря современным языком, угол — это фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла.
Острый (а), тупой (б) и прямой (в) углы. Острые и тупые углы также известны как косые углы.
В евклидовой геометрии углы используются для изучения многоугольников и треугольников, а также как самостоятельный объект изучения. Изучение углов треугольника или углов единичной окружности составляет основу тригонометрии.
В дифференциальной геометрии и исчислении углы между плоскими кривыми, пространственными кривыми или поверхностями можно вычислить с помощью производной.
Кривые
Кривая — это одномерный объект, который может быть прямым (как линия) или нет; кривые в 2-мерном пространстве называются плоскими кривыми, а кривые в 3-мерном пространстве называются пространственными кривыми.
В топологии кривая определяется функцией от интервала действительных чисел до другого пространства. В дифференциальной геометрии используется то же определение, но определяющая функция должна быть дифференцируемой. Алгебраическая геометрия изучает алгебраические кривые, которые определяются как алгебраические многообразия размерности один.
Поверхности
Сфера — это поверхность, которую можно задать параметрически (посредством x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ ) or implicitly (by x 2 + y 2 + z 2 − r 2 = 0.)
Поверхность — это двумерный объект, такой как сфера или параболоид. В дифференциальной геометрии и топологии поверхности описываются двумерными «участками» (или окрестностями), которые собираются диффеоморфизмами или гомеоморфизмами соответственно. В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
Многообразия
Главная страница: Многообразие
Многообразие является обобщением понятий кривой и поверхности. В топологии многообразие — это топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную евклидову пространству. В дифференциальной геометрии дифференцируемое многообразие — это пространство, каждая окрестность которого диффеоморфна евклидову пространству.
Многообразия широко используются в физике, в том числе в общей теории относительности и теории струн
Топологии и метрики
Главная страница: Топология
Визуальная проверка теоремы Пифагора для треугольника (3, 4, 5), как в Zhoubi Suanjing 500–200 г. до н.э. Теорема Пифагора является следствием евклидовой метрики.
Топология — это математическая структура множества, которая сообщает, как элементы множества пространственно соотносятся друг с другом. Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Конструкции компаса и линейки
Главная страница: Конструкции компаса и линейки
Классические геометры уделяли особое внимание построению геометрических объектов, которые были описаны другим способом. Классически единственными инструментами, разрешенными в геометрических построениях, являются циркуль и линейка. Кроме того, каждое построение должно было быть завершено за конечное число шагов. Однако некоторые задачи оказалось трудно или невозможно решить только этими средствами, и были найдены остроумные конструкции с использованием парабол и других кривых, а также механических устройств.
Размер
Главная страница: Размер
Снежинка Коха с фрактальной размерностью = log4/log3 и топологической размерностью = 1
Там, где традиционная геометрия допускала измерения 1 (линия), 2 (плоскость) и 3 (наш окружающий мир, воспринимаемый как трехмерное пространство), математики использовали более высокие измерения в течение почти двух столетий. Измерение прошло через этапы превращения в любое натуральное число n , возможно бесконечное с введением гильбертова пространства, и в любое положительное действительное число во фрактальной геометрии. Теория размерности — это техническая область, изначально входящая в общую топологию, в которой обсуждаются определения ; как и большинство математических идей, размерность теперь определяется, а не интуиция. Связные топологические многообразия имеют четко определенную размерность; это скорее теорема (инвариантность области), чем что-либо априорное .
Вопрос размерности по-прежнему важен для геометрии, несмотря на отсутствие полных ответов на классические вопросы. Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Симметрия
Главная страница: Симметрия
Мозаика гиперболической плоскости
Тема симметрии в геометрии почти так же стара, как и сама геометрическая наука. Симметричные формы, такие как круг, правильные многоугольники и платоновые тела, имели большое значение для многих древних философов и подробно исследовались еще до Евклида. Симметричные узоры встречаются в природе и были художественно воспроизведены во множестве форм, в том числе в графике М. К. Эшера. Тем не менее, только во второй половине 19 в.века, когда была признана объединяющая роль симметрии в основаниях геометрии. Эрлангенская программа Феликса Кляйна провозгласила, что в очень точном смысле симметрия, выраженная через понятие группы преобразования, определяет, какая геометрия есть . Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Другим типом симметрии является принцип двойственности в проективной геометрии (см. Двойственность (проективная геометрия)) среди других областей. Это метафеномен можно примерно описать так: в любой теореме поменяйте точку на плоскость , соедините с и , лежит в , а содержит , и вы получите столь же истинную теорему. Аналогичная и тесно связанная форма двойственности существует между векторным пространством и его дуальным пространством.
Неевклидова геометрия
Дифференциальная геометрия использует инструменты исчисления для изучения проблем, связанных с кривизной.
За почти две тысячи лет после Евклида, в то время как круг геометрических вопросов, задаваемых и ответов, неизбежно расширялся, основное понимание пространства оставалось в основном тем же самым. Иммануил Кант утверждал, что существует только одна абсолютная геометрия, истинность которой известна априорно внутренней способностью ума: евклидова геометрия была априорно синтетической. Этот господствующий взгляд был опрокинут революционным открытием неевклидовой геометрии в работах Бойяи, Лобачевского и Гаусса (так и не опубликовавшего свою теорию). Они продемонстрировали, что обычное евклидово пространство — лишь одна из возможностей развития геометрии. Широкое видение предмета геометрии было затем выражено Риманом в его инаугурационной лекции 1867 г. Über die Hypothesen, welche der Geometrie zu Grunde liegen ( О гипотезах, на которых основана геометрия ), опубликовано только после его смерти. Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Связанные страницы
- Топология
Картинки для детей
Европейец и араб, практикующие геометрию в 15 веке
Женщина преподает геометрию . Иллюстрация в начале средневекового перевода «Начал» Евклида (ок. 1310 г.).
Утолщение узла трилистник
Quintic Калаби-Яу тройной
Медресе Бу Инания, Фес, Марокко, мозаичные плитки зеллидж, образующие сложные геометрические мозаики
Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Цитируйте эту статью:
Факты о геометрии для детей. Энциклопедия Киддла.
Энциклопедия Киддла.
Факты о геометрии для детей
Уроки геометрии в 20 веке
Геометрия — это разновидность математики, изучающая размер, форму и положение вещей. В геометрии есть плоские (2D) формы и твердые (3D) формы. Квадраты, круги и треугольники — одни из самых простых фигур в плоской геометрии. Кубы, цилиндры, конусы и сферы — простые фигуры в объемной геометрии.
Содержание
- Применение
- Происхождение
- Примеры
- Важные понятия геометрии
- Аксиомы
- Очки
- строк
- Самолеты
- Уголки
- Кривые
- Поверхности
- Коллекторы
- Топологии и метрики
- Конструкции компаса и линейки
- Размер
- Симметрия
- Неевклидова геометрия
- Связанные страницы
- Картинки для детей
Использование
Геометрия может использоваться для измерения площади и периметра плоской формы. Его также можно использовать для измерения объема и площади поверхности твердого тела.
Его также можно использовать для измерения объема и площади поверхности твердого тела.
Геометрия может быть использована для расчета размера и формы многих вещей. Например, геометрия может помочь людям найти:
- площадь дома, чтобы они могли купить нужное количество краски
- объем коробки, чтобы узнать, достаточно ли она велика, чтобы вместить литр еды
- площадь фермы, поэтому ее можно разделить на равные части
- расстояние по краю пруда, чтобы знать, сколько ограждения купить.
Происхождение
Геометрия зародилась как искусство измерения формы земли, чтобы ее можно было справедливо разделить между людьми. Слово «геометрия» означает «измерять землю». Из этого она выросла и стала одной из важнейших частей математики. Греческий математик Евклид написал первую книгу по геометрии. Геометрия — один из древнейших разделов математики.
Примеры
Геометрия начинается с нескольких простых идей, которые считаются истинными и называются аксиомами. Например:
Например:
- Точку изображают на бумаге, касаясь ее карандашом или ручкой без каких-либо боковых движений. Мы знаем, где находится точка, но она не имеет размера.
- Прямая линия — это кратчайшее расстояние между двумя точками. Например, Софи тянет веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.
- Плоскость — это плоская поверхность, которая не останавливается ни в каком направлении. Например, представьте себе стену, бесконечно простирающуюся во всех направлениях.
Важные понятия геометрии
Ниже приведены некоторые из наиболее важных понятий геометрии.
Аксиомы
Иллюстрация постулата параллельности Евклида
- См. Также: Евклидова геометрия
Евклид использовал абстрактный подход к геометрии в своих «Элементах», одной из самых влиятельных когда-либо написанных книг. Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Точки
Главная страница: Точка (геометрия)
Точки считаются фундаментальными объектами в евклидовой геометрии. Они были определены различными способами, включая определение Евклида как «то, что не имеет частей», а также с помощью алгебры или вложенных множеств. Во многих областях геометрии, таких как аналитическая геометрия, дифференциальная геометрия и топология, все объекты считаются построенными из точек. Однако некоторые исследования геометрии проводились без привязки к точкам.
Однако некоторые исследования геометрии проводились без привязки к точкам.
Линии
Главная страница: Линия (геометрия)
Евклид описал линию как «длину без ширины», которая «равномерна по отношению к точкам на самой себе». В современной математике, учитывая множество геометрий, понятие линии тесно связано со способом описания геометрии. Например, в аналитической геометрии линия на плоскости часто определяется как множество точек, координаты которых удовлетворяют заданному линейному уравнению, но в более абстрактных условиях, таких как геометрия инцидентности, линия может быть независимым объектом, отличным от множество точек, лежащих на нем. В дифференциальной геометрии геодезическая — это обобщение понятия линии на искривленные пространства.
Плоскости
Плоскость (геометрия)
Плоскость — это плоская двумерная поверхность, простирающаяся бесконечно далеко. Плоскости используются во всех областях геометрии. Например, плоскости можно изучать как топологическую поверхность без привязки к расстояниям или углам; его можно изучать как аффинное пространство, где можно изучать коллинеарность и отношения, но не расстояния; его можно изучать как комплексную плоскость с использованием методов комплексного анализа; и так далее.
Уголки
Main page: Angle
Евклид определяет плоский угол как наклон друг к другу в плоскости двух прямых, которые пересекаются и не лежат прямо относительно друг друга. Говоря современным языком, угол — это фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла.
Острый (а), тупой (б) и прямой (в) углы. Острые и тупые углы также известны как косые углы.
В евклидовой геометрии углы используются для изучения многоугольников и треугольников, а также как самостоятельный объект изучения. Изучение углов треугольника или углов единичной окружности составляет основу тригонометрии.
В дифференциальной геометрии и исчислении углы между плоскими кривыми, пространственными кривыми или поверхностями можно вычислить с помощью производной.
Кривые
Кривая — это одномерный объект, который может быть прямым (как линия) или нет; кривые в 2-мерном пространстве называются плоскими кривыми, а кривые в 3-мерном пространстве называются пространственными кривыми.
В топологии кривая определяется функцией от интервала действительных чисел до другого пространства. В дифференциальной геометрии используется то же определение, но определяющая функция должна быть дифференцируемой. Алгебраическая геометрия изучает алгебраические кривые, которые определяются как алгебраические многообразия размерности один.
Поверхности
Сфера — это поверхность, которую можно задать параметрически (посредством x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ ) or implicitly (by x 2 + y 2 + z 2 − r 2 = 0.)
Поверхность — это двумерный объект, такой как сфера или параболоид. В дифференциальной геометрии и топологии поверхности описываются двумерными «участками» (или окрестностями), которые собираются диффеоморфизмами или гомеоморфизмами соответственно. В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
Многообразия
Главная страница: Многообразие
Многообразие является обобщением понятий кривой и поверхности. В топологии многообразие — это топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную евклидову пространству. В дифференциальной геометрии дифференцируемое многообразие — это пространство, каждая окрестность которого диффеоморфна евклидову пространству.
Многообразия широко используются в физике, в том числе в общей теории относительности и теории струн
Топологии и метрики
Главная страница: Топология
Визуальная проверка теоремы Пифагора для треугольника (3, 4, 5), как в Zhoubi Suanjing 500–200 г. до н.э. Теорема Пифагора является следствием евклидовой метрики.
Топология — это математическая структура множества, которая сообщает, как элементы множества пространственно соотносятся друг с другом. Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Конструкции компаса и линейки
Главная страница: Конструкции компаса и линейки
Классические геометры уделяли особое внимание построению геометрических объектов, которые были описаны другим способом. Классически единственными инструментами, разрешенными в геометрических построениях, являются циркуль и линейка. Кроме того, каждое построение должно было быть завершено за конечное число шагов. Однако некоторые задачи оказалось трудно или невозможно решить только этими средствами, и были найдены остроумные конструкции с использованием парабол и других кривых, а также механических устройств.
Размер
Главная страница: Размер
Снежинка Коха с фрактальной размерностью = log4/log3 и топологической размерностью = 1
Там, где традиционная геометрия допускала измерения 1 (линия), 2 (плоскость) и 3 (наш окружающий мир, воспринимаемый как трехмерное пространство), математики использовали более высокие измерения в течение почти двух столетий. Измерение прошло через этапы превращения в любое натуральное число n , возможно бесконечное с введением гильбертова пространства, и в любое положительное действительное число во фрактальной геометрии. Теория размерности — это техническая область, изначально входящая в общую топологию, в которой обсуждаются определения ; как и большинство математических идей, размерность теперь определяется, а не интуиция. Связные топологические многообразия имеют четко определенную размерность; это скорее теорема (инвариантность области), чем что-либо априорное .
Вопрос размерности по-прежнему важен для геометрии, несмотря на отсутствие полных ответов на классические вопросы. Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Симметрия
Главная страница: Симметрия
Мозаика гиперболической плоскости
Тема симметрии в геометрии почти так же стара, как и сама геометрическая наука. Симметричные формы, такие как круг, правильные многоугольники и платоновые тела, имели большое значение для многих древних философов и подробно исследовались еще до Евклида. Симметричные узоры встречаются в природе и были художественно воспроизведены во множестве форм, в том числе в графике М. К. Эшера. Тем не менее, только во второй половине 19 в.века, когда была признана объединяющая роль симметрии в основаниях геометрии. Эрлангенская программа Феликса Кляйна провозгласила, что в очень точном смысле симметрия, выраженная через понятие группы преобразования, определяет, какая геометрия есть . Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Другим типом симметрии является принцип двойственности в проективной геометрии (см. Двойственность (проективная геометрия)) среди других областей. Это метафеномен можно примерно описать так: в любой теореме поменяйте точку на плоскость , соедините с и , лежит в , а содержит , и вы получите столь же истинную теорему. Аналогичная и тесно связанная форма двойственности существует между векторным пространством и его дуальным пространством.
Неевклидова геометрия
Дифференциальная геометрия использует инструменты исчисления для изучения проблем, связанных с кривизной.
За почти две тысячи лет после Евклида, в то время как круг геометрических вопросов, задаваемых и ответов, неизбежно расширялся, основное понимание пространства оставалось в основном тем же самым. Иммануил Кант утверждал, что существует только одна абсолютная геометрия, истинность которой известна априорно внутренней способностью ума: евклидова геометрия была априорно синтетической. Этот господствующий взгляд был опрокинут революционным открытием неевклидовой геометрии в работах Бойяи, Лобачевского и Гаусса (так и не опубликовавшего свою теорию). Они продемонстрировали, что обычное евклидово пространство — лишь одна из возможностей развития геометрии. Широкое видение предмета геометрии было затем выражено Риманом в его инаугурационной лекции 1867 г. Über die Hypothesen, welche der Geometrie zu Grunde liegen ( О гипотезах, на которых основана геометрия ), опубликовано только после его смерти. Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Связанные страницы
- Топология
Картинки для детей
Европейец и араб, практикующие геометрию в 15 веке
Женщина преподает геометрию . Иллюстрация в начале средневекового перевода «Начал» Евклида (ок. 1310 г.).
Утолщение узла трилистник
Quintic Калаби-Яу тройной
Медресе Бу Инания, Фес, Марокко, мозаичные плитки зеллидж, образующие сложные геометрические мозаики
Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Цитируйте эту статью:
Факты о геометрии для детей. Энциклопедия Киддла.
Энциклопедия Киддла.
Факты о геометрии для детей
Уроки геометрии в 20 веке
Геометрия — это разновидность математики, изучающая размер, форму и положение вещей. В геометрии есть плоские (2D) формы и твердые (3D) формы. Квадраты, круги и треугольники — одни из самых простых фигур в плоской геометрии. Кубы, цилиндры, конусы и сферы — простые фигуры в объемной геометрии.
Содержание
- Применение
- Происхождение
- Примеры
- Важные понятия геометрии
- Аксиомы
- Очки
- строк
- Самолеты
- Уголки
- Кривые
- Поверхности
- Коллекторы
- Топологии и метрики
- Конструкции компаса и линейки
- Размер
- Симметрия
- Неевклидова геометрия
- Связанные страницы
- Картинки для детей
Использование
Геометрия может использоваться для измерения площади и периметра плоской формы. Его также можно использовать для измерения объема и площади поверхности твердого тела.
Его также можно использовать для измерения объема и площади поверхности твердого тела.
Геометрия может быть использована для расчета размера и формы многих вещей. Например, геометрия может помочь людям найти:
- площадь дома, чтобы они могли купить нужное количество краски
- объем коробки, чтобы узнать, достаточно ли она велика, чтобы вместить литр еды
- площадь фермы, поэтому ее можно разделить на равные части
- расстояние по краю пруда, чтобы знать, сколько ограждения купить.
Происхождение
Геометрия зародилась как искусство измерения формы земли, чтобы ее можно было справедливо разделить между людьми. Слово «геометрия» означает «измерять землю». Из этого она выросла и стала одной из важнейших частей математики. Греческий математик Евклид написал первую книгу по геометрии. Геометрия — один из древнейших разделов математики.
Примеры
Геометрия начинается с нескольких простых идей, которые считаются истинными и называются аксиомами. Например:
Например:
- Точку изображают на бумаге, касаясь ее карандашом или ручкой без каких-либо боковых движений. Мы знаем, где находится точка, но она не имеет размера.
- Прямая линия — это кратчайшее расстояние между двумя точками. Например, Софи тянет веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.
- Плоскость — это плоская поверхность, которая не останавливается ни в каком направлении. Например, представьте себе стену, бесконечно простирающуюся во всех направлениях.
Важные понятия геометрии
Ниже приведены некоторые из наиболее важных понятий геометрии.
Аксиомы
Иллюстрация постулата параллельности Евклида
- См. Также: Евклидова геометрия
Евклид использовал абстрактный подход к геометрии в своих «Элементах», одной из самых влиятельных когда-либо написанных книг. Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.
Точки
Главная страница: Точка (геометрия)
Точки считаются фундаментальными объектами в евклидовой геометрии. Они были определены различными способами, включая определение Евклида как «то, что не имеет частей», а также с помощью алгебры или вложенных множеств. Во многих областях геометрии, таких как аналитическая геометрия, дифференциальная геометрия и топология, все объекты считаются построенными из точек. Однако некоторые исследования геометрии проводились без привязки к точкам.
Однако некоторые исследования геометрии проводились без привязки к точкам.
Линии
Главная страница: Линия (геометрия)
Евклид описал линию как «длину без ширины», которая «равномерна по отношению к точкам на самой себе». В современной математике, учитывая множество геометрий, понятие линии тесно связано со способом описания геометрии. Например, в аналитической геометрии линия на плоскости часто определяется как множество точек, координаты которых удовлетворяют заданному линейному уравнению, но в более абстрактных условиях, таких как геометрия инцидентности, линия может быть независимым объектом, отличным от множество точек, лежащих на нем. В дифференциальной геометрии геодезическая — это обобщение понятия линии на искривленные пространства.
Плоскости
Плоскость (геометрия)
Плоскость — это плоская двумерная поверхность, простирающаяся бесконечно далеко. Плоскости используются во всех областях геометрии. Например, плоскости можно изучать как топологическую поверхность без привязки к расстояниям или углам; его можно изучать как аффинное пространство, где можно изучать коллинеарность и отношения, но не расстояния; его можно изучать как комплексную плоскость с использованием методов комплексного анализа; и так далее.
Уголки
Main page: Angle
Евклид определяет плоский угол как наклон друг к другу в плоскости двух прямых, которые пересекаются и не лежат прямо относительно друг друга. Говоря современным языком, угол — это фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла.
Острый (а), тупой (б) и прямой (в) углы. Острые и тупые углы также известны как косые углы.
В евклидовой геометрии углы используются для изучения многоугольников и треугольников, а также как самостоятельный объект изучения. Изучение углов треугольника или углов единичной окружности составляет основу тригонометрии.
В дифференциальной геометрии и исчислении углы между плоскими кривыми, пространственными кривыми или поверхностями можно вычислить с помощью производной.
Кривые
Кривая — это одномерный объект, который может быть прямым (как линия) или нет; кривые в 2-мерном пространстве называются плоскими кривыми, а кривые в 3-мерном пространстве называются пространственными кривыми.
В топологии кривая определяется функцией от интервала действительных чисел до другого пространства. В дифференциальной геометрии используется то же определение, но определяющая функция должна быть дифференцируемой. Алгебраическая геометрия изучает алгебраические кривые, которые определяются как алгебраические многообразия размерности один.
Поверхности
Сфера — это поверхность, которую можно задать параметрически (посредством x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ ) or implicitly (by x 2 + y 2 + z 2 − r 2 = 0.)
Поверхность — это двумерный объект, такой как сфера или параболоид. В дифференциальной геометрии и топологии поверхности описываются двумерными «участками» (или окрестностями), которые собираются диффеоморфизмами или гомеоморфизмами соответственно. В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
В алгебраической геометрии поверхности описываются полиномиальными уравнениями.
Многообразия
Главная страница: Многообразие
Многообразие является обобщением понятий кривой и поверхности. В топологии многообразие — это топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную евклидову пространству. В дифференциальной геометрии дифференцируемое многообразие — это пространство, каждая окрестность которого диффеоморфна евклидову пространству.
Многообразия широко используются в физике, в том числе в общей теории относительности и теории струн
Топологии и метрики
Главная страница: Топология
Визуальная проверка теоремы Пифагора для треугольника (3, 4, 5), как в Zhoubi Suanjing 500–200 г. до н.э. Теорема Пифагора является следствием евклидовой метрики.
Топология — это математическая структура множества, которая сообщает, как элементы множества пространственно соотносятся друг с другом. Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.
Конструкции компаса и линейки
Главная страница: Конструкции компаса и линейки
Классические геометры уделяли особое внимание построению геометрических объектов, которые были описаны другим способом. Классически единственными инструментами, разрешенными в геометрических построениях, являются циркуль и линейка. Кроме того, каждое построение должно было быть завершено за конечное число шагов. Однако некоторые задачи оказалось трудно или невозможно решить только этими средствами, и были найдены остроумные конструкции с использованием парабол и других кривых, а также механических устройств.
Размер
Главная страница: Размер
Снежинка Коха с фрактальной размерностью = log4/log3 и топологической размерностью = 1
Там, где традиционная геометрия допускала измерения 1 (линия), 2 (плоскость) и 3 (наш окружающий мир, воспринимаемый как трехмерное пространство), математики использовали более высокие измерения в течение почти двух столетий. Измерение прошло через этапы превращения в любое натуральное число n , возможно бесконечное с введением гильбертова пространства, и в любое положительное действительное число во фрактальной геометрии. Теория размерности — это техническая область, изначально входящая в общую топологию, в которой обсуждаются определения ; как и большинство математических идей, размерность теперь определяется, а не интуиция. Связные топологические многообразия имеют четко определенную размерность; это скорее теорема (инвариантность области), чем что-либо априорное .
Вопрос размерности по-прежнему важен для геометрии, несмотря на отсутствие полных ответов на классические вопросы. Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.
Симметрия
Главная страница: Симметрия
Мозаика гиперболической плоскости
Тема симметрии в геометрии почти так же стара, как и сама геометрическая наука. Симметричные формы, такие как круг, правильные многоугольники и платоновые тела, имели большое значение для многих древних философов и подробно исследовались еще до Евклида. Симметричные узоры встречаются в природе и были художественно воспроизведены во множестве форм, в том числе в графике М. К. Эшера. Тем не менее, только во второй половине 19 в.века, когда была признана объединяющая роль симметрии в основаниях геометрии. Эрлангенская программа Феликса Кляйна провозгласила, что в очень точном смысле симметрия, выраженная через понятие группы преобразования, определяет, какая геометрия есть . Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Симметрия в классической евклидовой геометрии представлена конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.
Другим типом симметрии является принцип двойственности в проективной геометрии (см. Двойственность (проективная геометрия)) среди других областей. Это метафеномен можно примерно описать так: в любой теореме поменяйте точку на плоскость , соедините с и , лежит в , а содержит , и вы получите столь же истинную теорему. Аналогичная и тесно связанная форма двойственности существует между векторным пространством и его дуальным пространством.
Неевклидова геометрия
Дифференциальная геометрия использует инструменты исчисления для изучения проблем, связанных с кривизной.
За почти две тысячи лет после Евклида, в то время как круг геометрических вопросов, задаваемых и ответов, неизбежно расширялся, основное понимание пространства оставалось в основном тем же самым. Иммануил Кант утверждал, что существует только одна абсолютная геометрия, истинность которой известна априорно внутренней способностью ума: евклидова геометрия была априорно синтетической. Этот господствующий взгляд был опрокинут революционным открытием неевклидовой геометрии в работах Бойяи, Лобачевского и Гаусса (так и не опубликовавшего свою теорию). Они продемонстрировали, что обычное евклидово пространство — лишь одна из возможностей развития геометрии. Широкое видение предмета геометрии было затем выражено Риманом в его инаугурационной лекции 1867 г. Über die Hypothesen, welche der Geometrie zu Grunde liegen ( О гипотезах, на которых основана геометрия ), опубликовано только после его смерти. Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Новое представление Римана о пространстве оказалось решающим в общей теории относительности Эйнштейна, а риманова геометрия, которая рассматривает очень общие пространства, в которых определено понятие длины, является опорой современной геометрии.
Связанные страницы
- Топология
Картинки для детей
Европейец и араб, практикующие геометрию в 15 веке
Женщина преподает геометрию . Иллюстрация в начале средневекового перевода «Начал» Евклида (ок. 1310 г.).
Утолщение узла трилистник
Quintic Калаби-Яу тройной
Медресе Бу Инания, Фес, Марокко, мозаичные плитки зеллидж, образующие сложные геометрические мозаики
Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Цитируйте эту статью:
Факты о геометрии для детей. Энциклопедия Киддла.
Энциклопедия Киддла.
геометрия | Определение, история, основы, отрасли и факты
математиков греко-римского мира
Смотреть все СМИ
- Ключевые люди:
- Блез Паскаль Евклид Птолемей Пьер де Ферма Бернхард Риманн
- Похожие темы:
- топология Евклидова геометрия аналитическая геометрия дифференциальная геометрия проективная геометрия
Просмотреть весь соответствующий контент →
геометрия , раздел математики, изучающий форму отдельных объектов, пространственные отношения между различными объектами и свойства окружающего пространства. Это одна из старейших областей математики, возникшая в ответ на такие практические задачи, как геодезия, и ее название происходит от греческих слов, означающих «измерение Земли». В конце концов стало понятно, что геометрия не должна ограничиваться изучением плоских поверхностей (геометрия плоскостей) и жестких трехмерных объектов (геометрия тел), но что даже самые абстрактные мысли и образы могут быть представлены и развиты в геометрических терминах.
Эта статья начинается с краткого описания основных разделов геометрии, а затем переходит к обширному историческому анализу. Для получения информации о конкретных разделах геометрии см. Евклидова геометрия, аналитическая геометрия, проективная геометрия, дифференциальная геометрия, неевклидовы геометрии и топология.
Основные разделы геометрии
В некоторых древних культурах была разработана форма геометрии, приспособленная к отношениям между длинами, площадями и объемами физических объектов. Эта геометрия была систематизирована Евклидом в Elements около 300 г. до н.э. на основе 10 аксиом или постулатов, из которых несколько сотен теорем были доказаны дедуктивной логикой. Elements олицетворяли аксиоматико-дедуктивный метод на протяжении многих веков.
Аналитическая геометрия была инициирована французским математиком Рене Декартом (1596–1650), который ввел прямоугольные координаты для определения местоположения точек и для представления линий и кривых с помощью алгебраических уравнений. Алгебраическая геометрия — это современное расширение предмета на многомерные и неевклидовы пространства.
Алгебраическая геометрия — это современное расширение предмета на многомерные и неевклидовы пространства.
Тест «Британника»
Тест «Все о математике»
Ваш учитель алгебры был прав. Вы будете использовать математику после выпуска — для этой викторины! Посмотрите, что вы помните из школы, и, возможно, узнаете несколько новых фактов в процессе.
Проективная геометрия была создана французским математиком Жираром Дезаргом (1591–1661) для изучения тех свойств геометрических фигур, которые не изменяются при проецировании их изображения или «тени» на другую поверхность.
Немецкий математик Карл Фридрих Гаусс (1777–1855) в связи с практическими задачами съемки и геодезии положил начало дифференциальной геометрии. Используя дифференциальное исчисление, он охарактеризовал внутренние свойства кривых и поверхностей. Например, он показал, что внутренняя кривизна цилиндра такая же, как у плоскости, в чем можно убедиться, разрезав цилиндр вдоль его оси и сплющив, но не такая, как у сферы, которую нельзя сплющить без искажение.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Начиная с 19-го века, различные математики заменяли альтернативами постулат параллельности Евклида, который в его современной форме гласит: «данные линия и точка, не лежащие на прямой, можно провести ровно одну прямую через данная точка параллельна прямой». Они надеялись показать, что альтернативы логически невозможны. Вместо этого они обнаружили, что существуют непротиворечивые неевклидовы геометрии.
Топология
Топология, самый молодой и сложный раздел геометрии, фокусируется на свойствах геометрических объектов, которые остаются неизменными при непрерывной деформации — сжатии, растяжении и складывании, но не разрыве. Непрерывное развитие топологии началось с 1911 г., когда голландский математик Л.Э.Й. Брауэр (1881–1966) представил методы, обычно применимые к этой теме.
История геометрии
Самые ранние из известных недвусмысленных примеров письменных источников, датируемых Египтом и Месопотамией около 3100 г. до н. контейнеры. Начиная примерно с VI века до н.1289 гео («Земля») и метрон («мера») для измерения Земли.
до н. контейнеры. Начиная примерно с VI века до н.1289 гео («Земля») и метрон («мера») для измерения Земли.
В дополнение к описанию некоторых достижений древних греков, в частности логического развития Евклидом геометрии в Элементах , в этой статье рассматриваются некоторые применения геометрии в астрономии, картографии и живописи от классической Греции до средневекового ислама и Европы эпохи Возрождения. . Он завершается кратким обсуждением расширений неевклидовой и многомерной геометрии в современную эпоху.
Древняя геометрия: практическая и эмпирическая
Происхождение геометрии лежит в заботах повседневной жизни. Традиционное описание, сохранившееся в «Истории » Геродота года (V век до н. э.), приписывает египтянам изобретение геодезии для восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекало из необходимости оценивать дань, хранить масло и зерно, строить плотины и пирамиды. Даже три непонятные геометрические задачи древности — удвоить куб, разделить угол на три части и возвести в квадрат круг — все они будут обсуждаться позже — вероятно, возникли из практических вопросов, из религиозного ритуала, хронометража и конструирования, соответственно, в догреческих обществ Средиземноморья. И главный предмет позднейшей греческой геометрии, теория конических сечений, обязан своим общим значением, а может быть, и своим происхождением, своему применению к оптике и астрономии.
Даже три непонятные геометрические задачи древности — удвоить куб, разделить угол на три части и возвести в квадрат круг — все они будут обсуждаться позже — вероятно, возникли из практических вопросов, из религиозного ритуала, хронометража и конструирования, соответственно, в догреческих обществ Средиземноморья. И главный предмет позднейшей греческой геометрии, теория конических сечений, обязан своим общим значением, а может быть, и своим происхождением, своему применению к оптике и астрономии.
Хотя многие древние люди, известные и неизвестные, внесли свой вклад в эту тему, никто не мог сравниться с влиянием Евклида и его Элементов геометрии, книги, которой уже 2300 лет и которая является объектом столь же болезненного и кропотливого изучения, как Библия. Однако о Евклиде известно гораздо меньше, чем о Моисее. На самом деле, единственное, что известно с достаточной степенью достоверности, это то, что Евклид преподавал в Александрийской библиотеке во времена правления Птолемея I (323–285/283 до н. э.). Евклид писал не только по геометрии, но и по астрономии и оптике, а может быть, и по механике и музыке. Только Elements , который был тщательно скопирован и переведен, сохранился без изменений.
э.). Евклид писал не только по геометрии, но и по астрономии и оптике, а может быть, и по механике и музыке. Только Elements , который был тщательно скопирован и переведен, сохранился без изменений.
Элементы Евклида были настолько полны и ясно написаны, что буквально стерли работу его предшественников. То, что известно о греческой геометрии до него, исходит главным образом из фрагментов, цитируемых Платоном и Аристотелем, а также более поздними математиками и комментаторами. Среди других ценных предметов они сохранили некоторые результаты и общий подход Пифагора ( ок. 580– в. 500 до н.э.) и его последователи. Пифагорейцы убедили себя, что все вещи являются числами или обязаны своими отношениями числам. Учение придавало математике первостепенное значение в исследовании и понимании мира. Платон развил подобный взгляд, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключе к толкованию вселенной. Таким образом, древняя геометрия ассоциировалась с возвышенным, дополняя свое земное происхождение и свою репутацию образца точного рассуждения.
Таким образом, древняя геометрия ассоциировалась с возвышенным, дополняя свое земное происхождение и свою репутацию образца точного рассуждения.
Нахождение прямого угла
Древние строители и геодезисты должны были уметь строить прямые углы в полевых условиях по требованию. Метод, применяемый египтянами, принес им в Греции прозвище «дергальщики каната», по-видимому, потому, что они использовали веревку для выкладки своих строительных инструкций. Один из способов, которым они могли использовать веревку для построения прямоугольных треугольников, заключался в том, чтобы пометить веревку с петлями узлами, чтобы, если ее удерживать за узлы и туго натягивать, веревка образовывала прямоугольный треугольник. Самый простой способ выполнить трюк — взять веревку длиной 12 звеньев, завязать 3 звена с одного конца и еще 5 звеньев с другого конца, а затем связать концы вместе, чтобы получилась петля. Однако египетские писцы не оставили нам указаний об этих процедурах, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой, противоположной прямому углу, равен сумме квадратов на двух других. стороны. Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Требуемые прямые углы были сделаны из веревок, размеченных для получения триад (3, 4, 5) и (5, 12, 13).
стороны. Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Требуемые прямые углы были сделаны из веревок, размеченных для получения триад (3, 4, 5) и (5, 12, 13).
В вавилонских глиняных табличках ( ок. 1700–1500 гг. до н. э.) современные историки обнаружили задачи, решения которых указывают на то, что теорема Пифагора и некоторые специальные триады были известны более чем за тысячу лет до Евклида. Однако случайный прямоугольный треугольник вряд ли будет иметь все стороны, измеряемые одной и той же единицей измерения, то есть каждая сторона будет целым числом, кратным некоторой общепринятой единице измерения. Этот факт, который был шокирован, когда его обнаружили пифагорейцы, породил концепцию и теорию несоизмеримости.
Обнаружение недоступных
Согласно древней традиции, Фалес Милетский, живший до Пифагора в 6 веке до н.э., изобрел способ измерения недоступных высот, таких как египетские пирамиды. Хотя ни одно из его сочинений не сохранилось, Фалес, возможно, хорошо знал о вавилонском наблюдении, что для подобных треугольников (треугольников, имеющих одинаковую форму, но не обязательно одинаковый размер) длина каждой соответствующей стороны увеличивается (или уменьшается) на одно и то же кратное число. Древние китайцы пришли к измерению недоступных высот и расстояний другим путем, используя «дополнительные» прямоугольники, как показано на следующем рисунке, который, как можно показать, дает результаты, эквивалентные результатам греческого метода с использованием треугольников.
Хотя ни одно из его сочинений не сохранилось, Фалес, возможно, хорошо знал о вавилонском наблюдении, что для подобных треугольников (треугольников, имеющих одинаковую форму, но не обязательно одинаковый размер) длина каждой соответствующей стороны увеличивается (или уменьшается) на одно и то же кратное число. Древние китайцы пришли к измерению недоступных высот и расстояний другим путем, используя «дополнительные» прямоугольники, как показано на следующем рисунке, который, как можно показать, дает результаты, эквивалентные результатам греческого метода с использованием треугольников.
Оценка богатства
Вавилонская клинописная табличка, написанная около 3500 лет назад, посвящена проблемам плотин, колодцев, водяных часов и раскопок. В нем также есть упражнение с круглыми ограждениями с подразумеваемым значением π = 3. Подрядчик бассейна царя Соломона, который построил пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение. Однако евреи должны были взять свое π у египтян до того, как переплыли Красное море, ибо папирус Райнда ( г. 2000 г. до н.э.; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.
2000 г. до н.э.; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.
Знание площади круга имело практическое значение как для чиновников, следивших за данью фараона, так и для строителей алтарей и бассейнов. Ахмес, писец, скопировавший и комментировавший папирус Райнда ( ок. 1650 гг. до н. э.), может многое сказать о цилиндрических зернохранилищах и пирамидах, целых и усеченных. Он мог вычислить их объемы, и, как следует из того, что он взял египетские секед , горизонтальное расстояние, связанное с вертикальным подъемом в один локоть, как определяющая величина для наклона пирамиды, он кое-что знал о подобных треугольниках.
Бернхард Риман | | Британика
Бернхард Риман
Смотреть все СМИ
- Дата рождения:
- 17 сентября 1826 г. Германия
- Умер:
- 20 июля 1866 г. (39 лет)) Италия
- Предметы изучения:
- Гипотеза Римана Дзета-функция Римана многообразие пространство единая теория поля
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
Бернхард Риман , полностью Георг Фридрих Бернхард Риман , (родился 17 сентября 1826, Бреселенц, Ганновер [Германия] — умер 20 июля 1866, Селаска, Италия), немецкий математик, чей глубокий и новый подход к изучение геометрии заложило математическую основу теории относительности Альберта Эйнштейна. Он также внес важный вклад в теорию функций, комплексный анализ и теорию чисел.
Он также внес важный вклад в теорию функций, комплексный анализ и теорию чисел.
Риман родился в бедной семье лютеранского пастора и всю жизнь был застенчивым и замкнутым человеком. Ему повезло иметь школьного учителя, который признал его редкие математические способности и давал ему книги для чтения, в том числе « Теория чисел » Адриана-Мари Лежандра (1830). Риман прочитал книгу за неделю, а затем заявил, что знает ее наизусть. Он продолжал изучать математику в Геттингенском университете в 1846–47 и 1849–1851 годах и в Берлинском университете (ныне Берлинский университет имени Гумбольдта) в 1847–49 годах.. Затем он постепенно продвигался по академической профессии, занимая череду низкооплачиваемых должностей, пока не стал профессором в 1859 году и впервые в своей жизни обрел определенную финансовую безопасность. Однако в 1862 году, вскоре после женитьбы на Элизе Кох, Риман серьезно заболел туберкулезом. Неоднократные поездки в Италию не смогли остановить развитие болезни, и он умер в Италии в 1866 году.
Викторина «Британника»
Наука: правда или вымысел?
Вас увлекает физика? Устали от геологии? С помощью этих вопросов отделите научный факт от вымысла.
Визиты Римана в Италию сыграли важную роль в развитии там современной математики; Энрико Бетти, в частности, занялся изучением римановых идей. Плохое здоровье помешало Риману опубликовать все свои работы, и некоторые из его лучших были опубликованы только посмертно — например, первое издание Римана Gesammelte mathematische Werke (1876; «Собрание математических трудов») под редакцией Рихарда Дедекинда и Генриха Вебера.
Влияние Римана изначально было меньше, чем могло бы быть. Геттинген был маленьким университетом, Риман был плохим лектором, и, что еще хуже, несколько его лучших студентов умерли молодыми. Его немногочисленные статьи также трудно читать, но его работа завоевала уважение некоторых из лучших математиков Германии, в том числе его друга Дедекинда и его соперника в Берлине Карла Вейерштрасса. Другие математики постепенно привлекались к его статьям своей интеллектуальной глубиной, и таким образом он поставил перед собой цель концептуального мышления, а не остроумных вычислений. Этот акцент был подхвачен Феликсом Кляйном и Давидом Гильбертом, которые позже сделали Геттинген мировым центром математических исследований с Карлом Гауссом и Риманом в качестве его знаковых фигур.
Другие математики постепенно привлекались к его статьям своей интеллектуальной глубиной, и таким образом он поставил перед собой цель концептуального мышления, а не остроумных вычислений. Этот акцент был подхвачен Феликсом Кляйном и Давидом Гильбертом, которые позже сделали Геттинген мировым центром математических исследований с Карлом Гауссом и Риманом в качестве его знаковых фигур.
В своей докторской диссертации (1851 г.) Риман ввел способ обобщения изучения полиномиальных уравнений от двух действительных переменных на случай двух комплексных переменных. В реальном случае полиномиальное уравнение определяет кривую на плоскости. Поскольку комплексную переменную z можно рассматривать как пару действительных переменных x + i y (где i = квадратный корень из √−1), уравнение, включающее две комплексные переменные, определяет вещественную поверхность, теперь известная как риманова поверхность, простирается по плоскости. В 1851 г. и в своей более широко доступной статье 1857 г. Риман показал, как такие поверхности можно классифицировать по числу, позже названному родом, которое определяется максимальным числом замкнутых кривых, которые можно провести на поверхности, не разбивая ее на части. отдельные куски. Это одно из первых значительных применений топологии в математике.
и в своей более широко доступной статье 1857 г. Риман показал, как такие поверхности можно классифицировать по числу, позже названному родом, которое определяется максимальным числом замкнутых кривых, которые можно провести на поверхности, не разбивая ее на части. отдельные куски. Это одно из первых значительных применений топологии в математике.
В 1854 году Риман представил свои идеи по геометрии для получения официальной докторской степени в Геттингене; пожилой Гаусс был экзаменатором и был очень впечатлен. Риман утверждал, что фундаментальными составляющими геометрии являются пространство точек (называемое сегодня многообразием) и способ измерения расстояний вдоль кривых в пространстве. Он утверждал, что пространство не обязательно должно быть обычным евклидовым пространством и что оно может иметь любую размерность (он даже рассматривал пространства бесконечной размерности). Нет необходимости и в том, чтобы поверхность целиком рисовалась в трехмерном пространстве. Несколько лет спустя это вдохновило итальянского математика Эудженио Бельтрами на создание именно такого описания неевклидовой геометрии, первой физически правдоподобной альтернативы евклидовой геометрии. Идеи Римана пошли дальше и, как оказалось, обеспечили математическую основу четырехмерной геометрии пространства-времени в общей теории относительности Эйнштейна. Похоже, что к этим идеям Римана привела отчасти его неприязнь к концепции действия на расстоянии в современной физике и его желание наделить пространство способностью передавать такие силы, как электромагнетизм и гравитация.
Идеи Римана пошли дальше и, как оказалось, обеспечили математическую основу четырехмерной геометрии пространства-времени в общей теории относительности Эйнштейна. Похоже, что к этим идеям Римана привела отчасти его неприязнь к концепции действия на расстоянии в современной физике и его желание наделить пространство способностью передавать такие силы, как электромагнетизм и гравитация.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
В 1859 году Риман также ввел теорию сложных функций в теорию чисел. Он взял дзета-функцию, которую многие предшествующие математики изучали из-за ее связи с простыми числами, и показал, как рассматривать ее как сложную функцию. Тогда дзета-функция Римана принимает нулевое значение в отрицательных четных целых числах (так называемые тривиальные нули), а также в точках на определенной линии (называемой критической линией). Стандартные методы теории сложных функций, разработанные Огюстеном-Луи Коши во Франции и самим Риманом, дали бы много информации о распределении простых чисел, если бы можно было показать, что все нетривиальные нули лежат на этой прямой — гипотеза, известная как гипотеза Римана. гипотеза. Все нетривиальные нули, обнаруженные до сих пор, находились на критической линии. На самом деле было обнаружено, что на этой прямой лежит бесконечно много нулей. Таких частичных результатов было достаточно, чтобы показать, что количество простых чисел меньше любого числа x хорошо аппроксимируется x / ln x . Гипотеза Римана была одной из 23 проблем, которые Гильберт призвал математиков решить в своем знаменитом обращении 1900 года «Проблемы математики». За прошедшие годы все большее количество математических идей было построено на предположении, что гипотеза Римана верна; его доказательство или опровержение имело бы далеко идущие последствия и принесло бы мгновенную известность.
гипотеза. Все нетривиальные нули, обнаруженные до сих пор, находились на критической линии. На самом деле было обнаружено, что на этой прямой лежит бесконечно много нулей. Таких частичных результатов было достаточно, чтобы показать, что количество простых чисел меньше любого числа x хорошо аппроксимируется x / ln x . Гипотеза Римана была одной из 23 проблем, которые Гильберт призвал математиков решить в своем знаменитом обращении 1900 года «Проблемы математики». За прошедшие годы все большее количество математических идей было построено на предположении, что гипотеза Римана верна; его доказательство или опровержение имело бы далеко идущие последствия и принесло бы мгновенную известность.
Риман по-новому взглянул на то, что означает существование математических объектов. Он искал общие доказательства существования, а не «конструктивные доказательства», которые действительно производят объекты. Он считал, что такой подход приводит к концептуальной ясности и не дает математику запутаться в деталях, но даже некоторые специалисты не соглашались с такими неконструктивными доказательствами.




 Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).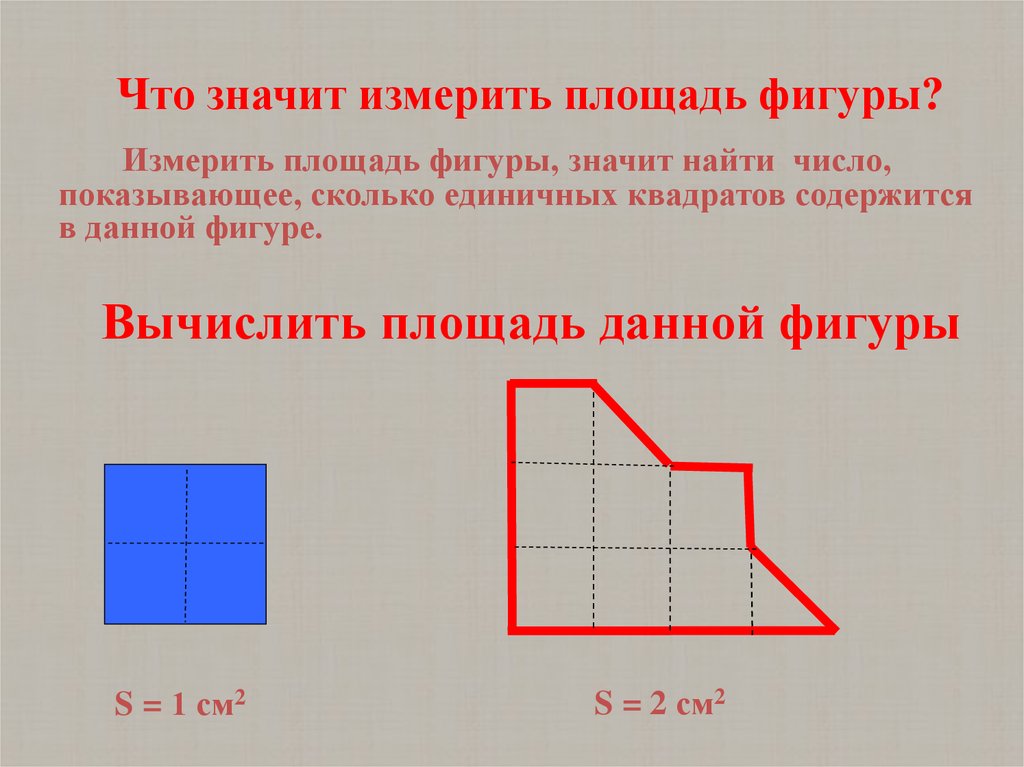

 Все правила по сольфеджио
Все правила по сольфеджио
 Биссектрисы смежных углов перпендикулярны.
Биссектрисы смежных углов перпендикулярны. Угол между ними равен
Угол между ними равен Тогда
Тогда

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.007 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.007 с.)