Напряжённость магнитного поля — Википедия

Материал из Википедии — свободной энциклопедии

Напряжённость магни́тного по́ля — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Обычно обозначается символом Н.

В Международной системе единиц (СИ):

H=1μ0B−M,{\displaystyle \mathbf {H} ={\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} ,}

где μ0{\displaystyle \mu _{0}} — магнитная постоянная.

В системе СГС:

H=B−4πM.{\displaystyle \mathbf {H} =\mathbf {B} -4\pi \mathbf {M} .}

В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот, намагниченность M зависит линейно от приложенного магнитного поля с индукцией B:

M=αB.{\displaystyle \mathbf {M} =\alpha \mathbf {B} .}

Однако исторически принято эту линейную зависимость описывать не коэффициентом α{\displaystyle \alpha }, а использовать связанные величины — магнитную восприимчивость χ{\displaystyle \chi } или магнитную проницаемость μ{\displaystyle \mu }:

M=χ1+4πχB=μ−14πμB.{\displaystyle \mathbf {M} ={\frac {\chi }{1+4\pi \chi }}\mathbf {B} ={\frac {\mu -1}{4\pi \mu }}\mathbf {B} .}

В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.

1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.

1 А/м = 4π/1000 Э ≈ 0,01256637 Э.

В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля (Н) совпадает с вектором магнитной индукции (B) с точностью до коэффициента, равного 1 в СГС и μ0{\displaystyle \mu _{0}} в СИ.

В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как, например, в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором магнитной индукции B₀ поля, которое было бы создано этой катушкой при отсутствии сердечника. B₀ в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.

При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля

H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём состоит её ценность: ведь H создает так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).

Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля^[1]. Энергия магнитного поля как такового выражается только через фундаментальную величину B. Тем не менее видно, что величина H феноменологическая и тут весьма удобна.

1. ↑ Для иллюстрации раскроем выражение для плотности энергии поля в среде wsubst{\displaystyle w_{subst}} в случае линейной связи намагниченности от напряженности магнитного поля M=χH.{\displaystyle \mathbf {M} =\chi \mathbf {H} .} В системе СИwsubst=12H⋅B=12(1μ0B−M)⋅B=12μ0B2−12M⋅B,{\displaystyle w_{subst}={\frac {1}{2}}\mathbf {H} \cdot \mathbf {B} ={\frac {1}{2}}({\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} )\cdot \mathbf {B} ={\frac {1}{2\mu _{0}}}\mathbf {B} ^{2}-{\frac {1}{2}}\mathbf {M} \cdot \mathbf {B} ,}где первый член — энергия магнитного поля, второй — энергия взаимодействия поля со средой (например, с магнитными диполями парамагнетика).

• Иродов И. Е. Основные законы электромагнетизма. — 2-е, стереотипное. — Москва: Высшая школа, 1991.

Магнитное поле планет — Википедия

Наличие или отсутствие у космических тел магнитного поля связывают с их внутренним строением.

Постоянное магнитное поле невозможно, так как температура в ядрах планет Солнечной системы намного выше точки Кюри. Было предложено множество объяснений природы внутреннего магнетизма планет; такие как термоэлектрический эффект или магнитные монополи не имеют удовлетворительных физических оснований, либо дают поля, по величине гораздо меньшие наблюдаемых. На настоящий момент общепринятой является теория магнитогидродинамического динамо: магнитное поле генерируется благодаря конвекционным потокам в жидком токопроводящем ядре^[1]. Она была предложена в 1919 году Дж. Лармором (на тот момент для объяснения магнетизма солнечных пятен)^[2], затем теоретические основы теории были разработаны У. Элсассером^[en] в 1939 году^[3] и Э. Белордом^[en] в 1949 году^[4].

Таким образом, необходимым условием генерации магнитного поля является наличие жидкого ядра, проводящего ток, причём в нём должны иметь место потоки. Правда, касательно их происхождения нет столь существенной определённости, как по поводу теории магнитного динамо в целом; так, например, предлагались гипотезы о прецессии и приливных силах. Однако наиболее вероятной причиной таких потоков и, как следствие, источником энергии, компенсирующим потери на тепловое рассеяние, является термохимическая конвекция^[5]. Показано, что в её отсутствие магнитное поле Земли затухало бы в e{\displaystyle e} раз за каждые 15000 лет, что ничтожно мало по сравнению с возрастом Земли — 4,5 млрд. лет^[1]. Кроме того, именно отсутствие конвективных потоков, судя по всему, ответственно за слабость магнитного поля Венеры^[6].

Магнитное поле тел Солнечной системы изучается как экспериментально — путём космических исследований — так и теоретически — посредством моделирования. Последнее требует решения системы нелинейных уравнений в частных производных (уравнение Навье-Стокса, уравнение магнитной индукции и др.), включающих параметры, значения которых в условиях ядер планет исключительно малы. Так, число Экмана, выражающее отношение величин вязкости и силы Кориолиса, составляет порядка 10⁻¹⁵, а магнитное число Прандтля, отвечающее за отношение вязкости к силе Лоренца — 10⁻⁶. Эти значения пока недостижимы как в численном моделировании, так и в экспериментах по воссозданию магнитного динамо в лабораторных условиях. Последние тем не менее полезны в плане понимания механизма^[1].

Магнитное поле планет и спутников планет Солнечной системы[править | править код]

Планеты Солнечной системы делятся на 3 группы: земной группы, некоторые из которых имеют жидкое металлическое ядро; газовые гиганты Юпитер и Сатурн, преимущественно состоящие из водорода и гелия; и ледяные гиганты Уран и Нептун с толстой газовой атмосферой, но имеющие также в составе более тяжёлые элементы, чем Солнце. Больше всего данных о магнитном поле Земли, так как наблюдения более точны и имеют более давнюю историю; сейсмологические исследования позволяют получить информацию о внутреннем строении нашей планеты^[1].

Меркурий[править | править код]

Имея довольно большое (что было подтверждено относительно недавно^[7]) жидкое ядро, Меркурий обладает магнитным полем, генерируемым по тому же механизму, что и в Земле, хотя и далеко не таким сильным^[8]. Сильный эксцентриситет орбиты и близость к Солнцу создают приливные эффекты и циркуляцию в крупном ядре планеты. Сказываться может и спин-орбитальный резонанс 3:2.

Венера[править | править код]

У Венеры и Земли близки размеры, средняя плотность и даже внутреннее строение, тем не менее, Земля имеет достаточно сильное магнитное поле, а Венера — нет (магнитный момент Венеры не превышает 5—10 % магнитного поля Земли). По одной из современных теорий напряженность дипольного магнитного поля зависит от прецессии полярной оси и угловой скорости вращения. Именно эти параметры на Венере ничтожно малы, но измерения указывают на ещё более низкую напряжённость, чем предсказывает теория. Современные предположения по поводу слабого магнитного поля Венеры состоят в том, что в предположительно железном ядре Венеры отсутствуют конвективные потоки

[6]^[9]. Это, в свою очередь, может объясняться отсутствием тектоники плит, причина которого также пока не ясна. Возможно, это отсутствие воды, играющей в этом процессе роль своего рода смазывающего вещества^[10][11]. Или же, возможно, вследствие высокой температуры кора не затвердевает, и из-за этого либо не могут сформироваться плиты, подобные земным, либо становится более активным вулканизм, ввиду чего недостаточно энергии для конвективного движения потоков в ядре ^[12]. С другой стороны, возможно, что, наоборот, воды на поверхности Венеры нет именно из-за отсутствия магнитного поля^[13]. У Венеры нет крупных спутников, способных вызвать приливные процессы в ядре и мантии (как на Земле), так же ее орбита наиболее близка к круговой.

Марс[править | править код]

Сильный остаточный магнетизм Марса, открытый станцией Mars Global Surveyor^[14], свидетельствует о динамо, происходившем ранее и угасшем примерно через 350 млн лет после формирования планеты, судя по всему, вследствие отвердевания ядра^[1][15][16]. По одной из гипотез, вокруг Марса обращался крупный астероид, вызывавший приливные эффекты, не дающие остыть ядру. Потом астероид снизился до предела Роша и разрушился. Как следствие — остывание ядра, распад магнитного поля и угасание геологических процессов. Имеющиеся спутники слишком малы, чтобы вызвать гравитационные возмущения в недрах планеты. Так же планета находится довольно далеко от Солнца, несмотря на сильно эллиптическую орбиту.

Луна[править | править код]

Как и в случае Марса, ядро Луны полностью отвердело^[15], но в её коре обнаружены следы остаточного магнетизма. Это может также говорить о ранее функционировавшем динамо, но также возможно, что это последствия метеоритных ударов^[5][1]. Луна находится в приливном захвате с Землей (обращена все время одной стороной). Как следствие — Земля не вызывает приливных эффектов в недрах Луны, но сама Луна вызывает приливы в гидросфере, литосфере и мантии планеты. Это одна из возможных причин сохранения геологических процессов на Земле в активном состоянии. Иначе бы ядро Земли обладало минимальной температурой при массе Земли, да и вращалось бы ядро (возможно и вся Земля) медленнее, а оборот ядра и коры Земли были бы неравны, от этого произошли бы мощные землетрясения и извержения вулканов. В частности Земля обладает исключительно мощным магнитным полем из планет земной группы.

[источник не указан 439 дней]

Ганимед[править | править код]

Доказано, что это единственный спутник, внутри которого происходит активное динамо, как в Земле и Меркурии, вследствие конвективных потоков в жидком проводящем ядре (вероятно, оно осталось таким благодаря приливному разогреву из-за орбитального резонанса и гравитации Юпитера^[17]). Ось его магнитного диполя направлена против магнитного момента Юпитера. Кроме того, Ганимед обладает и индуцированным полем, вызванным его движением в сильном магнитном поле Юпитера^[18][19].

Другие спутники планет-гигантов[править | править код]

Ни один из остальных крупных спутников Солнечной системы не имеет сильного генерируемого внутренними источниками магнитного поля. На внутренних спутниках Юпитера наблюдается только индуцированное поле^[1].

Юпитер и Сатурн[править | править код]

Планеты-гиганты не имеют ядер, состоящих преимущественно из железа, однако в ядрах Юпитера и Сатурна находится водород в жидкой металлической фазе. Быстрое вращение этих ядер приводит к запуску динамо, создающему сильное магнитное поле. Ось его диполя у Юпитера, как и у Земли, наклонена примерно на 10° относительно оси вращения

[20], а у Сатурна практически совпадает с ней^[15][21].

Уран и Нептун[править | править код]

Магнитные поля Урана и Нептуна, в отличие от всех остальных планет Солнечной системы, являются не дипольными, а квадрупольными, то есть они имеют по 2 северных и 2 южных полюса^[22][21][23]. В их ядрах проводниками тока являются ионы; в целом природа их полей до конца не ясна^[15]. Возможно, они формируются на относительно малых глубинах, например, в океане жидкого аммиака, в тонкой конвективной оболочке, окружающей жидкую внутреннюю часть, имеющую стабильную слоистую структуру^[24].

1. ↑ ^{1 2 3 4 5 6 7} Chris A. Jones. Planetary Magnetic Fieldsand Fluid Dynamos (англ.) // Annual Review of Fluid Mechanics (англ.)русск.. — Annual Reviews, 2011. — Vol. 43. — P. 583—614.
2. ↑ Larmor, J. How could a rotating body such as the Sun become a magnet // Reports of the British Association. — 1919. — Т. 87. — С. 159—160.
3. ↑ Walter M. Elsasser. On the Origin of the Earth’s Magnetic Field : [англ.] // Phys. Rev.. — 1939. — Т. 55, вып. 5 (1 March). — С. 489—498. — DOI:10.1103/PhysRev.55.489.
4. ↑ E. C. Bullard. The Magnetic Field within the Earth : [англ.] // Proc. R. Soc. Lond. A. — 1949. — Т. 197, вып. 1051 (7 July). — С. 433—453. — DOI:10.1098/rspa.1949.0074.
5. ↑ ^{1 2} D J Stevenson. Planetary magnetic fields // Reports on Progress in Physics. — 1983. — Т. 46, № 5. — С. 555. — DOI:10.1088/0034-4885/46/5/001.
6. ↑
   1 ² Venus: Magnetic Field and Magnetosphere Архивная копия от 21 декабря 2008 на Wayback Machine (англ.) — J. G. Luhmann and C. T. Russel, UCLA
7. ↑ Gold, Lauren. Mercury has molten core, Cornell researcher shows (неопр.). Cornell University (3 мая 2007). Дата обращения 7 апреля 2008. Архивировано 22 мая 2012 года.
8. ↑ Christensen U. R. A deep dynamo generating Mercury’s magnetic field (англ.) // Nature. — 2006. — Vol. 444. — DOI:10.1038/nature05342. — PMID 17183319.  (Проверено 12 июня 2011)
9. ↑ Francis Nimmo. Why does Venus lack a magnetic field? : [англ.] // Geology. — 2002. — Т. 30, вып. 11 (November). — С. 987—990. — DOI:10.1130/0091-7613(2002)030<0987:WDVLAM>2.0.CO;2.
10. ↑ Jim Brau. Venus: Earth’s Sister Planet (англ.). Course «Astronomy 121: Solar System» (Spring 2011). University of Oregon (2011). Дата обращения 15 августа 2017.
11. ↑ Mian, Z.U. and Tozer, D.C. No water, no plate tectonics: convective heat transfer and the planetary surfaces of Venus and Earth : [англ.] // Terra Nova. — 1990. — Т. 2, вып. 5 (September). — С. 455—459. — DOI:10.1111/j.1365-3121.1990.tb00102.x.
12. ↑ Xiang-Dong Li. Venus’s Magnetic Field and Internal Structure (англ.). School of astronomy and space science, Nanjing University. Дата обращения 15 августа 2017.
13. ↑ Howard Falcon-Lang. Life on Earth: Is our planet special? (англ.), BBC News (9 December 2011). Дата обращения 15 августа 2017.
14. ↑ Acuna MH, Connerney JE, Ness NF, Lin RP, Mitchell D, Carlson CW, McFadden J, Anderson KA, Reme H, Mazelle C, Vignes D, Wasilewski P, Cloutier P. Global distribution of crustal magnetization discovered by the mars global surveyor MAG/ER experiment : [англ.] // Science. — 1999. — Т. 284, вып. 5415 (30 April). — С. 790—793. — DOI:10.1126/science.284.5415.790.
15. ↑ ^{1 2 3 4} Nigel Weiss. Dynamos in planets, stars and galaxies (англ.) // A&G. — 2002. — 1 июня (т. 43, вып. 3). — С. 3.9—3.14. — DOI:10.1029/2000RG000102.
16. ↑ Valentine, Theresa; Amde, Lishan. Magnetic Fields and Mars (неопр.). Mars Global Surveyor @ NASA (9 ноября 2006). Дата обращения 17 июля 2009. Архивировано 21 августа 2011 года.
17. ↑ Bland; Showman, A.P.; Tobie, G. Ganymede’s orbital and thermal evolution and its effect on magnetic field generation (англ.) // Lunar and Planetary Society Conference : journal. — 2007. — March (vol. 38). — P. 2020.
18. ↑ Kivelson, M.G.; Khurana, K.K.; Coroniti, F.V. et al. The magnetic field and magnetosphere of Ganymede (англ.) // Geophys. Res. Lett. (англ.)русск. : journal. — 1997. — Vol. 24, no. 17. — P. 2155—2158. — DOI:10.1029/97GL02201. — Bibcode: 1997GeoRL..24.2155K.
19. ↑ Kivelson, M.G.; Khurana, K.K.; Coroniti, F.V. et al. The Permanent and Inductive Magnetic Moments of Ganymede (англ.) // Icarus : journal. — Elsevier, 2002. — Vol. 157, no. 2. — P. 507—522. — DOI:10.1006/icar.2002.6834. — Bibcode: 2002Icar..157..507K.
20. ↑ Brainerd, Jim. Jupiter’s Magnetosphere, The Astrophysics Spectator (22 ноября 2004). Дата обращения 10 июня 2017.
21. ↑ ^{1 2} Russell, C.T. Planetary Magnetospheres (англ.) // Rep. Prog. Phys. (англ.)русск. : journal. — 1993. — Vol. 56. — P. 687—732.
22. ↑ «Планетные системы»: Уран
23. ↑ Ness, Norman F.; Acuna, Mario H.; Behannon, Kenneth W.; et al. Magnetic Fields at Uranus (англ.) // Science. — 1986. — Vol. 233. — P. 85—89.
24. ↑ Stanley, Sabine; Bloxham, Jeremy. Convective-region geometry as the cause of Uranus’ and Neptune’s unusual magnetic fields (англ.) // Nature : journal. — 2004. — Vol. 428. — P. 151—153. — DOI:10.1038/nature02376. Архивировано 7 августа 2007 года. Архивная копия от 7 августа 2007 на Wayback Machine

Основные характеристики магнитного поля | Электрикам

Магнитное поле представляет собой особую форму материи которая проявляется через механическое взаимодействие токов и через возникновение ЭДС в проводниках движущихся в этом поле. Оно обнаруживается вокруг движущихся электрических зарядов, следовательно и вокруг проводника с током.

Графическое изображение магнитного поля

Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми.

Для того что бы определить направление магнитного поля можно воспользоваться магнитной стрелкой, или правилом буравчика.

Правило буравчика

Основные характеристики магнитного поля

Магнитная индукция B  — это векторная величина определяющая силу действующую на заряженную частицу со стороны магнитного поля. Измеряется в теслах Тл.

           

B = Ф/S

            

  магнитная постоянная.

µ — относительная магнитная проницаемость — табличная величина (для вакуума = 1)

Магнитный поток Ф — скалярная физическая величина числено равная произведению магнитной индукции на площадь поверхности ограниченной замкнутым контуром. Измеряется в веберах Вб.

Магнитный поток через контур максимален,если плоскость контура перпендикулярна магнитному полю.

Тогда магнитный поток рассчитывается по формуле:

Φ_max = B · S

Магнитный поток через контур равен нулю,если контур располагается параллельно магнитному полю.

Напряженность H – это векторная величина независящая от магнитных свойств среды. Измеряется в ампер на метр А/М.

Магнитная проницаемость. Магнитная индукция зависит не только от силы тока, проходящего по проводнику или катушке, но и от свойств среды, в которой создается магнитное поле. Величиной, характеризующей магнитные свойства среды, служит магнитная проницаемость_.

Магнитное поле звёзд — Википедия

Звёздное магнитное поле — магнитное поле, создаваемое движением проводящей плазмы внутри звёзд главной последовательности. Это движение создаётся путём конвекции, которая является одной из форм переноса энергии из центра звезды к её поверхности с помощью физического перемещения материала. Локальные магнитные поля воздействуют на плазму, в результате чего намагниченные области поднимаются по отношению к остальной части поверхности, и могут достичь даже фотосферы звезды. Этот процесс создаёт звёздные пятна на поверхности звезды (по аналогии с солнечными пятнами), и связанное с этим появление корональных петель^[1].

Спектр на нижнем рисунке демонстрирует эффект Зеемана после того как магнитное поле воздействует на источник. На верхнем рисунке показаны линии поглощения в отсутствии магнитного поля

Магнитное поле звезды может быть измерено с помощью эффекта Зеемана. Обычно атомы в атмосфере звезды поглощают энергию на определённой частоте электромагнитного спектра, производя характерные тёмные линии поглощения в спектре. Однако, когда атомы находятся в магнитном поле, эти линии расщепляются на несколько, близкорасположенных линий. Также появляется поляризация электромагнитного излучения звезды, которая зависит от ориентации магнитного поля. Таким образом, сила и направление магнитного поля звезды может быть определена путём изучения линий в эффекте Зеемана^[2][3].

Звёздный спектрополяриметр используется для измерения магнитного поля звезды. Этот инструмент состоит из спектрографа в сочетании с поляриметром. Первый инструмент, с помощью которого изучалось магнитное поле звёзд, был NARVAL, который был установлен на телескопе Бернара Лио, работавшего в обсерватории на горе Пик-дю-Миди во французских Пиренеях^[4].

Различные измерения, включая магнитометрические измерения за последние 150 лет^[5]: ¹⁴С в кольцах деревьев и ¹⁰Ве в кернах льда^[6], установили существенную изменчивость магнитного поля Солнца на десятилетних, столетних и тысячелетних временных отрезках^[7].

Магнитные поля звёзд, согласно теории солнечного динамо, вызваны движением вещества в конвективной зоне звезды. Эта конвективная циркуляция проводящей плазмы разрушает изначальное магнитное поле звезды, а затем создаёт дипольные магнитные поля звезды. Так как звезда испытывает дифференциальное вращение для различных широт, то магнитные линии в форме тора окружают звезду. Магнитные линии могут стать местом высокой концентрации энергии, являющейся причиной активности звезды, когда они выходят на её поверхность^[8].

Магнитное поле вращающегося проводящего газа или жидкости генерирует самоусиливающиеся электрические токи и связанные с ними магнитные поля, вследствие сочетания дифференциального вращения (вращения с разными угловыми скоростями на различных широтах звезды), силы Кориолиса и индукции. Распределение токов может быть достаточно сложным, с многочисленными открытыми и закрытыми петлями, и, таким образом магнитное поле этих токов в непосредственной близости от них также достаточно сложно распределено. На больших расстояниях, однако, магнитные поля токов, текущих в противоположных направлениях взаимно компенсируются, и остаются только дипольные поля, медленно уменьшающиеся с расстоянием. Поскольку основной ток движется в направлении вращения звезды (экваториальных течений), основной компонент порождённого магнитного поля направлен перпендикулярно экватору, создавая магнитные полюса вблизи географических полюсов вращающегося тела.

Магнитные поля всех небесных тел, часто согласуются с направлением вращения, с заметными исключениями, такими как некоторые пульсары. Ещё одна особенность этой модели динамо в том, что токи, скорее переменные, а не постоянные. Их направление, и, следовательно, направление магнитного поля, которое они производят, испытывают более или менее периодические, изменения амплитуды и направления, хотя и совмещённые с осью вращения.

Основной компонент магнитного поля Солнца меняет направление каждые 11 лет (т. е. с периодом около 22 лет), в результате чего изменяется величина магнитной активности Солнца. Во время покоя, активность максимальна, пятен мало (из-за отсутствия магнитного торможения плазмы) и, как результат, происходит массовый выброс плазмы высокой энергии в солнечную корону, а затем в межпланетное пространство. Столкновения солнечных пятен с противоположно направленными магнитными полями генерирует сильные электрические поля вблизи быстро исчезающих регионов выхода на поверхность магнитного поля. Это электрическое поле ускоряет электроны и протоны высоких энергий (кэВ) в результате чего струи чрезвычайно горячей плазмы покидают поверхность Солнца и нагревают солнечную корону до огромных температур (миллионы кельвинов).

Если газ или жидкость очень вязкие (в результате дифференциального турбулентного движения), изменение магнитного поля может быть не строго периодическим. Так обстоит дело с магнитным полем Земли, которое порождается турбулентным течением в вязком слое над внутренним ядром.

Возникновение звёздного пятна: магнитные линии проникают сквозь поверхность звезды

Звёздные пятна являются регионами интенсивной магнитной активности на поверхности звезды. Они являются формами видимой составляющей магнитных потоков, которые образуются в конвективной зоне звезды. Из-за дифференциального вращения звёзд, потоки приобретают форму тора и растягиваются, препятствуя конвекции, и, как следствие, образуют зоны с температурой ниже, чем у остального вещества^[9]. Корональные петли часто образуются над звёздными пятнами, формируясь вдоль силовых линий магнитного поля, которые поднимаются над поверхностью в корону звезды. В свою очередь, они разогревают корону до температур свыше миллиона кельвинов^[10].

Корональные петли, связанные со звёздными пятнами и протуберанцы, связанные со вспышками звезды, становятся причинами выбросов корональной массы. Плазма нагревается до десятков миллионов градусов, частицы с поверхности звезды ускоряются до экстремальных скоростей ^[11].

Поверхностная активность, по современным представлениям, связаны с возрастом и скоростью вращения звёзд главной последовательности. Молодые звёзды с большой скоростью вращения обладают сильной магнитной активностью. В отличие от них, звёзды среднего возраста, подобные Солнцу с медленной скоростью вращения показывают низкий уровень активности, который циклически меняется. Некоторые старые звёзды не проявляют практически никакой активности, что может означать, что они вступили в период затишья, сопоставимое с минимумом Маундера. Измерения времени изменения звёздной магнитной активности может быть полезно для определения скорости дифференциального вращения звезды^[12].

Поверхностное магнитное поле звезды SU Возничего (молодая звезды типа Т Тельца), реконструированное с помощью эффекта Зеемана-Доплера

Звёзды типа Т Тельца является одним из видов звёзд ещё не вышедших на главную последовательность, т. е.они разогревается посредством гравитационного сжатия, а не водородного горения в их ядрах. Они являются переменными магнитно-активными звёздами. Магнитное поле таких звёзд, взаимодействует с их сильным звёздным ветром, передавая момент импульса окружающему звезду протопланетному диску, что служит причиной снижения скорости вращения звезды^[13].

Красные карлики спектрального класса M (0.1-0.6 массы Солнца), демонстрирующие быструю, нерегулярную переменность, известны как вспыхивающие звёзды. Эти колебания яркости, вызваны вспышками, чья активность значительно сильнее, чем можно предположить по размеру звезды. Вспышки звёзд этого класса могут увеличить поверхность звезды на 20%, и излучают большую часть своей энергии в синей и ультрафиолетовой части спектра^[14].

Планетарные туманности появляются, когда красный гигант сбрасывает свою внешнюю оболочку, образуя расширяющийся газовый пузырь. Однако остаётся загадкой, почему эти пузыри не всегда сферически симметричны. 80% планетарных туманностей не имеют сферической формы, а вместо этого образуют биполярные или эллиптические туманности. Одна из гипотез формирования несферической формы — влияние магнитного поля звезды. Вместо равномерного расширения во всех направлениях, выброшенная плазма стремится вытянуться вдоль магнитных линий. Наблюдения центральной звезды, по крайней мере, четырёх планетарных туманностей подтвердили, что они действительно обладают мощными магнитными полями^[15].

Схематическое изображение пульсара. Сфера в центре изображения — нейтронная звезда, кривые линии обозначают линии магнитного поля пульсара, голубые конусы — потоки излучения пульсара

После того как некоторые массивные звёзды прекратили термоядерный синтез в своих недрах, часть из них коллапсирует в компактные объекты, называемые нейтронные звёзды. Эти объекты сохраняют значительные магнитные поля, доставшиеся от звезды-прародителя. В результате коллапса размер звезды резко уменьшается на много порядков, а поскольку магнитный момент звезды сохраняется полностью, то напряжённость магнитного поля нейтронной звезды пропорционально возрастает на много порядков. Быстрое вращение нейтронных звёзд превращает их в пульсар, который испускает узкий пучок энергии.

Компактные и быстро вращающихся астрономические объекты (белые карлики, нейтронные звёзды и чёрные дыры) имеют чрезвычайно сильные магнитные поля. Магнитное поле новорождённой быстровращающейся нейтронной звезды настолько сильное (до 10⁸тесла), что излучаемой электромагнитной энергии достаточно, чтобы быстро (в течение нескольких миллионов лет) затормозить вращение звезды в 100, а то и 1000 раз. Материя, падающая на нейтронную звезду также должна двигаться вдоль силовых линий магнитного поля, в результате чего образуются два горячих пятна на поверхности звезды, где вещество сталкивается с поверхностью звезды. Эти пятна небольшие — буквально около метра в диаметре, но чрезвычайно яркие. Их периодические затмения во время вращения звезды, как предполагается, являются источником пульсирующего излучения (см. пульсар).

Экстремальная форма намагниченной нейтронной звезды называется магнетар. Они образуются в результате коллапса ядра при вспышке сверхновой^[16]. Существование таких звёзд было подтверждено в 1998 году при исследовании звезды SGR 1806-20. Магнитное поле этой звезды увеличило температуру поверхности до 18 млн К и она испускает огромное количество энергии в гамма-всплесках^[17].

Струи релятивистской плазмы часто наблюдаются в направлении магнитных полюсов активных ядер в центрах очень молодых галактик.

1. ↑ Brainerd, Jerome James X-rays from Stellar Coronas (неопр.). The Astrophysics Spectator (6 июля 2005). Архивировано 2 июля 2012 года. (англ.)
2. ↑ Wade, Gregg A. (July 8–13, 2004). «Stellar Magnetic Fields: The view from the ground and from space». The A-star Puzzle: Proceedings IAU Symposium No. 224: 235–243, Cambridge, England: Cambridge University Press.  (англ.)
3. ↑ Basri, Gibor. Big Fields on Small Stars (англ.) // Science. — 2006. — Vol. 311, no. 5761. — P. 618—619. — DOI:10.1126/science.1122815. — PMID 16456068. (англ.)
4. ↑ Staff. NARVAL: First Observatory Dedicated To Stellar Magnetism, Science Daily (22 февраля 2007). (англ.)
5. ↑ Lockwood, M.; Stamper, R.; Wild, M. N. A Doubling of the Sun’s Coronal Magnetic Field during the Last 100 Years (англ.) // Nature : journal. — 1999. — Vol. 399, no. 6735. — P. 437—439. — DOI:10.1038/20867. (англ.)
6. ↑ Beer, Jürg. Long-term indirect indices of solar variability (англ.) // Space Science Reviews : journal. — 2000. — Vol. 94, no. 1/2. — P. 53—66. — DOI:10.1023/A:1026778013901. (англ.)
7. ↑ Kirkby, Jasper. Cosmic Rays and Climate (неопр.) // Surveys in Geophysics. — 2007. — Т. 28. — С. 333—375. — DOI:10.1007/s10712-008-9030-6. (англ.)
8. ↑ Piddington, J. H. On the origin and structure of stellar magnetic fields (англ.) // Astrophysics and Space Science (англ.)русск. : journal. — 1983. — Vol. 90, no. 1. — P. 217—230. — DOI:10.1007/BF00651562. (англ.)
9. ↑ Sherwood, Jonathan. Dark Edge of Sunspots Reveal Magnetic Melee, University of Rochester (3 декабря 2002). (англ.)
10. ↑ Hudson, H. S.; Kosugi, T. How the Sun’s Corona Gets Hot (англ.) // Science. — 1999. — Vol. 285, no. 5429. — P. 849. — DOI:10.1126/science.285.5429.849. (англ.)
11. ↑ Hathaway, David H. Solar Flares (неопр.). NASA (18 января 2007). Архивировано 2 июля 2012 года. (англ.)
12. ↑ Berdyugina, Svetlana V. Starspots: A Key to the Stellar Dynamo (неопр.). Living Reviews (2005). Архивировано 2 июля 2012 года. (англ.)
13. ↑ Küker, M.; Henning, T.; Rüdiger, G. Magnetic Star-Disk Coupling in Classical T Tauri Systems (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2003. — Vol. 589. — P. 397—409. — DOI:10.1086/374408. (англ.)
14. ↑ Templeton, Matthew Variable Star Of The Season: UV Ceti (неопр.). AAVSO (Autumn 2003). Дата обращения 21 июня 2007. Архивировано 14 февраля 2007 года. (англ.)
15. ↑ Jordan, S.; Werner, K.; O’Toole, S.. First Detection Of Magnetic Fields In Central Stars Of Four Planetary Nebulae, Space Daily (6 января 2005). (англ.)
16. ↑ Duncan, Robert C. ‘Magnetars’, Soft Gamma Repeaters, and Very Strong Magnetic Fields (неопр.) (недоступная ссылка). University of Texas at Austin (2003). Архивировано 27 февраля 2012 года. (англ.) (англ.)
17. ↑ Isbell, D.; Tyson, T.. Strongest Stellar Magnetic Field yet Observed Confirms Existence of Magnetars, NASA/Goddard Space Flight Center (20 мая 1998). (англ.) (англ.)

МАГНИТНОЕ ПОЛЕ ЗЕМЛИ | Энциклопедия Кругосвет

Содержание статьи

МАГНИТНОЕ ПОЛЕ ЗЕМЛИ. Большинство планет Солнечной системы в той или иной степени обладают магнитными полями. По убыванию дипольного магнитного момента на первом месте Юпитер и Сатурн, а за ними следуют Земля, Меркурий и Марс, причем по отношению к магнитному моменту Земли значение их моментов составляет 20 000, 500, 1, 3/5000 3/10000. Дипольный магнитный момент Земли на 1970 составлял 7,98·10²⁵ Гс/см³ (или 8,3·10²² А.м²), уменьшаясь за десятилетие на 0,04·10²⁵ Гс/см³. Средняя напряженность поля на поверхности составляет около 0,5 Э (5·10^–5 Тл). По форме основное магнитное поле Земли до расстояний менее трех радиусов близко к полю эквивалентного магнитного диполя. Его центр смещен относительно центра Земли в направлении на 18° с.ш. и 147,8° в. д. Ось этого диполя наклонена к оси вращения Земли на 11,5°. На такой же угол геомагнитные полюса отстоят от соответствующих географических полюсов. При этом южный геомагнитный полюс находится в северном полушарии. В настоящее время он расположен недалеко от северного географического полюса Земли в Северной Гренландии. Его координаты j = 78,6 + 0,04° Т с.ш., l = 70,1 + 0,07° T з.д., где Т – число десятилетий от 1970. У cеверного магнитного полюса j = 75° ю.ш., l = 120,4° в.д. (в Антарктиде). Реальные магнитные силовые линии магнитного поля Земли в среднем близки к силовым линиям этого диполя, отличаясь от них местными нерегулярностями, связанными с наличием намагниченных пород в коре. В результате вековых вариаций геомагнитный полюс прецессирует относительно географического полюса с периодом около 1200 лет. На больших расстояниях магнитное поле Земли несимметрично. Под действием исходящего от Солнца потока плазмы (солнечного ветра) магнитное поле Земли искажается и приобретает «шлейф» в направлении от Солнца, который простирается на сотни тысяч километров, выходя за орбиту Луны.

Специальный раздел геофизики, изучающий происхождение и природу магнитного поля Земли называется геомагнетизмом. Геомагнетизм рассматривает проблемы возникновения и эволюции основной, постоянной составляющей геомагнитного поля, природа переменной составляющей (примерно 1% от основного поля), а так же структура магнитосферы – самых верхних намагниченных плазменных слоев земной атмосферы, взаимодействующих с солнечным ветром и защищающих Землю от космического проникающего излучения. Важной задачей является изучение закономерностей вариаций геомагнитного поля, поскольку они обусловлены внешними воздействиями, связанными в первую очередь с солнечной активностью.

Происхождение магнитного поля.

Наблюдаемые свойства магнитного поля Земли согласуются с представлением о его возникновении благодаря механизму гидромагнитного динамо. В этом процессе первоначальное магнитное поле усиливается в результате движений (обычно конвективных или турбулентных) электропроводящего вещества в жидком ядре планеты или в плазме звезды. При температуре вещества в несколько тысяч К его проводимость достаточно высока, чтобы конвективные движения, происходящие даже в слабо намагниченной среде, могли возбуждать изменяющиеся электрические токи, способные, в соответствии с законами электромагнитной индукции, создавать новые магнитные поля. Затухание этих полей либо создает тепловую энергию (по закону Джоуля), либо приводит к возникновению новых магнитных полей. В зависимости от характера движений эти поля могут либо ослаблять, либо усиливать исходные поля. Для усиления поля достаточно определенной асимметрии движений. Таким образом, необходимым условием гидромагнитного динамо является само наличие движений в проводящей среде, а достаточным – наличие определенной асимметрии (спиральности) внутренних потоков среды. При выполнении этих условий процесс усиления продолжается до тех пор, пока растущие с увеличением силы токов потери на джоулево тепло не уравновесят приток энергии, поступающей за счет гидродинамических движений.

Динамо-эффект – самовозбуждение и поддержание в стационарном состоянии магнитных полей вследствие движения проводящей жидкости или газовой плазмы. Его механизм подобен генерации электрического тока и магнитного поля в динамо-машине с самовозбуждением. С динамо-эффектом связывают происхождение собственных магнитных полей Солнца Земли и планет, а также их локальные поля, например, поля пятен и активных областей.

Составляющие геомагнитного поля.

Собственное магнитное поле Земли (геомагнитное поле) можно разделить на cледующие три основные части.

1. Основное магнитное поле Земли, испытывающее медленные изменения во времени (вековые вариации) с периодами от 10 до 10 000 лет, сосредоточенными в интервалах 10–20, 60–100, 600–1200 и 8000 лет. Последний связан с изменением дипольного магнитного момента в 1,5–2 раза.

2. Мировые аномалии – отклонения от эквивалентного диполя до 20% напряженности отдельных областей с характерными размерами до10 000 км. Эти аномальные поля испытывают вековые вариации, приводящие к изменениям со временем в течение многих лет и столетий. Примеры аномалий: Бразильская, Канадская, Сибирская, Курская. В ходе вековых вариаций мировые аномалии смещаются, распадаются и возникают вновь. На низких широтах имеется западный дрейф по долготе со скоростью 0,2° в год.

3. Магнитные поля локальных областей внешних оболочек с протяженностью от нескольких до сотен км. Они обусловлены намагниченностью горных пород в верхнем слое Земли, слагающих земную кору и расположенных близко к поверхности. Одна из наиболее мощных – Курская магнитная аномалия.

4. Переменное магнитное поле Земли (так же называемое внешним) определяется источниками в виде токовых систем, находящимися за пределами земной поверхности и в ее атмосфере. Основными источниками таких полей и их изменений являются корпускулярные потоки замагниченной плазмы, приходящие от Солнца вместе с солнечным ветром, и формирующие структуру и форму земной магнитосферы.

Структура магнитного поля земной атмосферы.

Земное магнитное поле находится под воздействием потока намагниченной солнечной плазмы. В результате взаимодействия с полем Земли образуется внешняя граница околоземного магнитного поля, называемая магнитопаузой. Она ограничивает земную магнитосферу. Из-за воздействия солнечных корпускулярных потоков размеры и форма магнитосферы постоянно меняются, и возникает переменное магнитное поле, определяемое внешними источниками. Его переменность обязана своим происхождением токовым системам, развивающимся на различных высотах от нижних слоев ионосферы до магнитопаузы. Изменения магнитного поля Земли во времени, вызванные различными причинами, называются геомагнитными вариациями, которые различаются как по своей длительности, так и по локализации на Земле и в ее атмосфере.

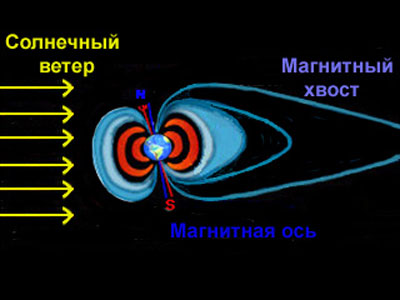
Магнитосфера – область околоземного космического пространства, контролируемая магнитным полем Земли. Магнитосфера формируется в результате взаимодействия солнечного ветра с плазмой верхних слоев атмосферы и магнитным полем Земли. По форме магнитосфера представляет собой каверну и длинный хвост, которые повторяют форму магнитных силовых линий. Подсолнечная точка в среднем находится на расстоянии 10 земных радиусов, а хвост магнитосферы простирается за орбиту Луны. Топология магнитосферы определяется областями вторжения солнечной плазмы внутрь магнитосферы и характером токовых систем.

Хвост магнитосферы образован силовыми линиями магнитного поля Земли, выходящими из полярных областей и вытянутых под действием солнечного ветра на сотни земных радиусов от Солнца в ночную сторону Земли. В итоге плазма солнечного ветра и солнечных корпускулярных потоков как бы обтекают земную магнитосферу, придавая ей своеобразную хвостатую форму. В хвосте магнитосферы, на больших расстояниях от Земли, напряженность магнитного поля Земли, а следовательно и их защитные свойства, ослабляются, и некоторые частицы солнечной плазмы получают возможность проникнуть и попасть во внутрь земной магнитосферы и магнитных ловушек радиационных поясов. Проникая в головную часть магнитосферы в область овалов полярных сияний под действием изменяющегося давления солнечного ветра и межпланетного поля, хвост служит местом формирования потоков высыпающихся частиц, вызывающих полярные сияния и авроральные токи. Магнитосфера отделена от межпланетного пространства магнитопаузой. Вдоль магнитопаузы частицы корпускулярных потоков обтекают магнитосферу. Влияние солнечного ветра на земное магнитное поле иногда бывает очень сильным. Магнитопауза – внешняя граница магнитосферы Земли (или планеты), на которой динамическое давление солнечного ветра уравновешивается давлением собственного магнитного поля. При типичных параметрах солнечного ветра подсолнечная точка удалена от центра Земли на 9–11 земных радиусов. В период магнитных возмущений на Земле магнитопауза может заходить за геостационарную орбиту (6,6 радиусов Земли). При слабом солнечном ветре подсолнечная точка находится на расстоянии 15–20 радиусов Земли.

Солнечный ветер –

истечение плазмы солнечной короны в межпланетное пространство. На уровне орбиты Земли средняя скорость частиц солнечного ветра (протонов и электронов) около 400 км/с, число частиц – несколько десятков в 1 см³.

Магнитная буря.

Локальные характеристики магнитного поля изменяются и колеблются иногда в течение многих часов, а потом восстанавливаются до прежнего уровня. Это явление называется магнитной бурей. Магнитные бури часто начинаются внезапно и одновременно по всему земному шару.

Геомагнитные вариации.

Изменение магнитного поля Земли во времени под действием различных факторов называются геомагнитными вариациями. Разность между наблюдаемой величиной напряженности магнитного поля и средним ее значением за какой-либо длительный промежуток времени, например, месяц или год, называется геомагнитной вариацией. Согласно наблюдениям, геомагнитные вариации непрерывно изменяются во времени, причем такие изменения часто носят периодический характер.

Cуточные вариации. Cуточные вариации геомагнитного поля возникают регулярно в основном за счет токов в ионосфере Земли, вызванных изменениями освещенности земной ионосферы Солнцем в течение суток.

Нерегулярные вариации. Нерегулярные вариации магнитного поля возникают вследствие воздействия потока солнечной плазмы (солнечного ветра) на магнитосферу Земли, а так же изменений внутри магнитосферы и взаимодействия магнитосферы с ионосферой.

27-дневные вариации. 27-дневные вариации существуют как тенденция к повторению увеличения геомагнитной активности через каждые 27 дней, соответствующих периоду вращения Солнца относительно земного наблюдателя. Эта закономерность связана с существованием долгоживущих активных областей на Солнце, наблюдаемых в течении нескольких оборотов Солнца. Эта закономерность проявляется в виде 27-дневной повторяемости магнитной активности и магнитных бурь.

Сезонные вариации. Сезонные вариации магнитной активности уверенно выявляются на основании среднемесячных данных о магнитной активности, полученных путем обработки наблюдений за несколько лет. Их амплитуда увеличивается с ростом общей магнитной активности. Найдено, что сезонные вариации магнитной активности имеют два максимума, соответствующие периодам равноденствий, и два минимума, соответствующие периодам солнцестояний. Причиной этих вариаций является образование активных областей на Солнце, которые группируются в зонах от 10 до 30° северной и южной гелиографических широт. Поэтому в периоды равноденствий, когда плоскости земного и солнечного экваторов совпадают, Земля наиболее подвержена действию активных областей на Солнце.

11-летние вариации. Наиболее ярко связь между солнечной активностью и магнитной активностью проявляется при сопоставлении длинных рядов наблюдений, кратных 11 летним периодам солнечной активности. Наиболее известной мерой солнечной активности является число солнечных пятен. Найдено, что в годы максимального количества солнечных пятен магнитная активность также достигает наибольшей величины, однако возрастание магнитной активности несколько запаздывает по отношению к росту солнечной, так что в среднем это запаздывание составляет один год.

Вековые вариации – медленные вариации элементов земного магнетизма с периодами от нескольких лет и более. В отличии от суточных, сезонных, и других вариаций внешнего происхождения, вековые вариации связаны с источниками, лежащими внутри земного ядра. Амплитуда вековых вариаций достигает десятков нТл/год, изменения среднегодовых значений таких элементов, названы вековым ходом. Изолинии вековых вариаций концентрируются вокруг нескольких точек – центры или фокусы векового хода, в этих центрах величина векового хода достигает максимальных значений.

Радиационные пояса и космические лучи.

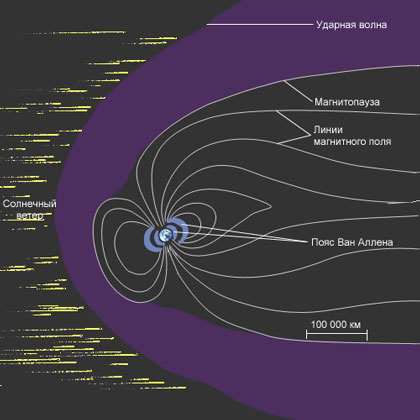
Радиационные пояса Земли – две области ближайшего околоземного космического пространства, которые в виде замкнутых магнитных ловушек окружают Землю.

В них сосредоточены огромные потоки протонов и электронов, захваченных дипольным магнитным полем Земли. Магнитное поле Земли оказывает сильное влияние на электрически заряженные частицы, движущиеся в околоземном космическом пространстве. Есть два основных источника возникновения этих частиц: космические лучи, т.е. энергичные (от 1 до12 ГэВ) электроны, протоны и ядра тяжелых элементов, приходящие с почти световыми скоростями, главным образом, из других частей Галактики. И корпускулярные потоки менее энергичных заряженных частиц (10⁵–10⁶ эВ), выброшенных Солнцем. В магнитном поле электрические частицы движутся по спирали; траектория частицы как бы навивается на цилиндр, по оси которого проходит силовая линия. Радиус этого воображаемого цилиндра зависит от напряженности поля и энергии частицы. Чем больше энергия частицы, тем при данной напряженности поля радиус (он называется ларморовским) больше. Если ларморовский радиус много меньше, чем радиус Земли, частица не достигает ее поверхности, а захватывается магнитным полем Земли. Если ларморовский радиус много больше, чем радиус Земли, частица движется так, как будто бы магнитного поля нет, частицы проникают сквозь магнитное поле Земли в экваториальных районах, если их энергия больше 10⁹ эв. Такие частицы вторгаются в атмосферу и вызывают при столкновении с ее атомами ядерные превращения, которые дают определенные количества вторичных космических лучей. Эти вторичные космические лучи уже регистрируются на поверхности Земли. Для исследования космических лучей в их первоначальной форме (первичных космических лучей) аппаратуру поднимают на ракетах и искусственных спутниках Земли. Примерно 99% энергичных частиц, «пробивающих» магнитный экран Земли, являются космическими лучами галактического происхождения и лишь около 1% образуется на Солнце. Магнитное поле Земли удерживает огромное число энергичных частиц, как электронов, так и протонов. Их энергия и концентрация зависят от расстояния до Земли и геомагнитной широты. Частицы заполняют как бы огромные кольца или пояса, охватывающие Землю вокруг геомагнитного экватора.

Эдвард Кононович

Магнитная индукция — Википедия

Материал из Википедии — свободной энциклопедии

Магни́тная инду́кция B→{\displaystyle {\vec {B}}} — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой F→{\displaystyle {\vec {F}}} магнитное поле действует на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}.

Более конкретно, B→{\displaystyle {\vec {B}}} — это такой вектор, что сила Лоренца F→{\displaystyle {\vec {F}}}, действующая со стороны магнитного поля^[1] на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}, равна

F→=q[v→×B→]{\displaystyle {\vec {F}}=q\left[{\vec {v}}\times {\vec {B}}\right]}

F=qvBsin⁡α{\displaystyle F=qvB\sin \alpha }

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора F→{\displaystyle {\vec {F}}} перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС единицей магнитной индукции является гаусс (Гс), в СИ — тесла (Тл)

1 Тл = 10⁴ Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в СИ, в виде для вакуума^[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике[править | править код]

В магнитостатическом пределе^[4] наиболее важными являются:

• Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

  B→(r→)=μ04π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

  B→(r→)=μ04π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

• Теорема Ампера о циркуляции магнитного поля^[5]:

  ∮∂S⁡B→⋅dl→=μ0IS≡μ0∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

  rotB→≡∇→×B→=μ0j→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае[править | править код]

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

divE→=ρε0,   rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=0,    rotB→=μ0j→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

divB→=0,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

rotB→=μ0j→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

F→=qE→+q[v→×B→],{\displaystyle {\vec {F}}=q{\vec {E}}+q\left[{\vec {v}}\times {\vec {B}}\right],}

Следствия из неё, такие как

• Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=[Idl→×B→],{\displaystyle d{\vec {F}}=\left[I{\vec {dl}}\times {\vec {B}}\right],}

dF→=[j→dV×B→],{\displaystyle d{\vec {F}}=\left[{\vec {j}}dV\times {\vec {B}}\right],}

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

• выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

• а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

• (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля

w=B22μ0{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

• Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:

   F→=qE→+q[v→×B→].{\displaystyle {\vec {F}}=q{\vec {E}}+q[{\vec {v}}\times {\vec {B}}].}

   При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведённую в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в статье далее).

Магнитный монополь — Википедия

Магни́тный монопо́ль — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля.

Магнитный монополь можно представлять как отдельно взятый полюс длинного и тонкого постоянного магнита. Однако у всех известных магнитов всегда два полюса, то есть он является диполем. Если разрезать магнит на две части, то у каждой его части по-прежнему будет два полюса. Все известные элементарные частицы, обладающие электромагнитным полем, являются магнитными диполями.

С созданием физики как науки, основанной на опыте, утвердилось мнение, что электрические и магнитные свойства тел существенно различаются. Это мнение было чётко выражено Уильямом Гильбертом в 1600 году. Установленное Шарлем Кулоном тождество законов притяжения и отталкивания для электрических зарядов и магнитных зарядов — полюсов магнитов, вновь подняло вопрос о сходстве электрических и магнитных сил, однако к концу XVIII века было выяснено, что в лабораторных условиях невозможно создать тело с ненулевым полным магнитным зарядом. Понятие о «магнитно заряженной субстанции» было надолго изгнано из физики после работы Ампера в 1820, в которой было доказано, что контур с электрическим током создаёт такое же магнитное поле, как магнитный диполь.

В 1894 году Пьер Кюри изложил в короткой заметке, что введение магнитных зарядов в уравнения Максвелла производится естественно и только делает их более симметричными.

Сформулированные Максвеллом уравнения классической электродинамики связывают электрическое и магнитное поля с движением заряженных частиц. Эти уравнения почти симметричны относительно электричества и магнетизма. Они могут быть сделаны полностью симметричными, если в дополнение к электрическому заряду qe{\displaystyle q_{\mathrm {e} }} и току ввести некий магнитный заряд qm{\displaystyle q_{\mathrm {m} }} (плотность магнитного заряда ρm{\displaystyle \rho _{\mathrm {m} }}) и магнитный ток (плотность магнитного тока jm{\displaystyle \mathbf {j} _{\mathrm {m} }}):

При этом изменённые уравнения с магнитными монополями переходят в классические уравнения при подстановке ρm=0{\displaystyle \rho _{\mathrm {m} }=0} и jm=0{\displaystyle \mathbf {j} _{\mathrm {m} }=0}, то есть если в рассматриваемой области пространства отсутствуют магнитные заряды. Таким образом можно создать систему уравнений Максвелла с учётом существования магнитных зарядов, при этом классические уравнения просто отражают тот факт, что обычно магнитные заряды не наблюдаются.

Если магнитные заряды существуют, то существование магнитных токов приведёт к существенным поправкам уравнений Максвелла, которые можно наблюдать на макроскопических масштабах.

В новой форме уравнений Максвелла возникают трудности математического описания при помощи вектор-потенциала. При наличии и магнитных и электрических зарядов электромагнитное поле не может быть описано при помощи вектор-потенциала Aμ{\displaystyle \mathbf {A} _{\mu }} (μ=0,1,2,3){\displaystyle (\mu =0,\;1,\;2,\;3)}, непрерывного во всём пространстве. Поэтому при наличии магнитных зарядов уравнения движения заряженных частиц не выводятся из вариационного принципа наименьшего действия. В классической электродинамике это не приводит к принципиальным трудностям (хотя и делает теорию несколько менее красивой), но квантовую динамику невозможно сформулировать вне рамок гамильтонова или лагранжева формализма. ^{[источник не указан 3696 дней]}

Поль Дирак предположил существование частицы с магнитным зарядом и пришёл к нетривиальному заключению, что магнитный заряд предполагаемого монополя не может иметь произвольного значения, но должен быть равен целому кратному определённого количества магнетизма.^[2]

Задача определения векторного потенциала A{\displaystyle A}, дающего магнитное поле H{\displaystyle H}, математически эквивалентна задаче определения системы токов j′{\displaystyle j’}, создающих магнитное поле H′{\displaystyle H’}. Из точки, испускающей постоянный поток магнитного поля, должен вытекать постоянный ток с равномерной плотностью во всех направлениях. Чтобы его поддерживать, надо по проводящей нити подводить ток к этой точке, равный току, исходящему из этой точки по всем направлениям, причем сила этого тока равна магнитному заряду g{\displaystyle g}.^[3] Поскольку расположение такой нити совершенно произвольно, то разность векторных потенциалов равна магнитному полю, создаваемому током, притекающим к точке по одной нити и утекающим по другой нити. Такое магнитное поле можно представить в виде многозначного потенциала, значение которого в каждой точке пространства изменяется при каждом обходе контура, связанного с нитью, на величину силы тока, умноженной на 4π{\displaystyle 4\pi }. Из квантовой механики известно, что волновая функция ψ{\displaystyle \psi }, характеризующая частицу с зарядом e{\displaystyle e} при изменении A→A+grad⁡f{\displaystyle A\rightarrow A+\operatorname {grad} f} как ψ→ψexp⁡(ieℏcf){\displaystyle \psi \rightarrow \psi \exp \left({\frac {ie}{\hbar c}}f\right)}. При обходе контура f=4πg{\displaystyle f=4\pi g}. Но при обходе контура волновая функция не должна измениться, поэтому exp⁡(ieℏc4πg)=1{\displaystyle \exp \left({\frac {ie}{\hbar c}}4\pi g\right)=1}. Комплексное число равно единице, если оно предствлено как exp⁡(2πin){\displaystyle \exp(2\pi in)}, где n{\displaystyle n} — произвольное целое число. Поэтому: ieℏc4πg=2πin{\displaystyle {\frac {ie}{\hbar c}}4\pi g=2\pi in}, где n{\displaystyle n} — целое число. Таким образом, магнитный заряд g{\displaystyle g} частицы должен быть кратен элементарному магнитному заряду g0=ℏc2e{\displaystyle g_{0}={\frac {\hbar c}{2e}}}, где e{\displaystyle e} — элементарный электрический заряд.^[4]

Примечательно обратное утверждение: существование магнитного заряда не противоречит стандартной квантовой механике только в том случае, если электрические заряды всех частиц квантуются. (Таким образом, существование в природе хотя бы одного магнитного монополя с определённым зарядом объяснило бы наблюдаемую на опыте кратность электрических зарядов частиц величине e{\displaystyle e}; магнитный заряд при этом тоже с необходимостью квантовался бы.)

Условие квантования Дирака обобщается на взаимодействие двух частиц, каждая из которых обладает как электрическим, так и магнитным зарядом (такие частицы называется дионами)

e1g2−e2g12πℏc=n.{\displaystyle {\frac {e_{1}g_{2}-e_{2}g_{1}}{2\pi \hbar c}}=n.}

(В используемой системе единиц e{\displaystyle e} и g{\displaystyle g} имеют одинаковую размерность, причём заряд e{\displaystyle e} фиксирован соотношением e2/4πℏc=1/137{\displaystyle e^{2}/4\pi \hbar c=1/137}.)

В нерелятивистском приближении сила, действующая на дион 1 с координатами r{\displaystyle r} и скоростью v{\displaystyle v} со стороны диона 2, закреплённого в начале координат, равна

F=(e1e2+g1g2)r+(e1g2−e2g1)[vr]c4πr3.{\displaystyle F={\frac {(e_{1}e_{2}+g_{1}g_{2})\mathbf {r} +(e_{1}g_{2}-e_{2}g_{1}){\dfrac {[\mathbf {vr} ]}{c}}}{4\pi r^{3}}}.}

Отметим, что входящие в эту формулу комбинации зарядов инвариантны относительно дуального преобразования.

В 1974 А. М. Поляков и Герард ‘т Хоофт (G. ‘t Hooft) независимо обнаружили^[5], что существование магнитного монополя не только возможно, но и обязательно в полевых теориях определённого класса. В моделях великого объединения, рассматривающих симметрию относительно фазовых преобразований волновых функций заряженных частиц как составную часть более широкой неабелевой калибровочной симметрии, электромагнитное поле связано с мультиплетом заряженных калибровочных полей X{\displaystyle X} с большими массами (эти массы возникают при спонтанном нарушении симметрии). Для некоторых калибровочных групп симметрии существуют устойчивые конфигурации полей X{\displaystyle X}, локализованные в области размером l<ℏ/MXc{\displaystyle l<\hbar /M_{X}c} и создающие вне этой области сферически симметричное магнитное поле. Существование таких конфигураций зависит от топологических свойств калибровочной группы, точнее, от того, каким образом в неё вложена подгруппа симметрии, сохранившейся после спонтанного нарушения. Стабильность этих магнитных монополей определяется особым поведением полей на больших расстояниях от центра. Масса магнитного монополя Mm{\displaystyle M_{m}} может быть вычислена, она зависит от конкретной полевой модели, однако во всяком случае должна быть большой, Mm≫MX{\displaystyle M_{m}\gg M_{X}} (по оценке, для широкого класса моделей Mm∼1016GeVc2{\displaystyle M_{m}\sim 10^{16}{\frac {GeV}{c^{2}}}}). Эти магнитные монополи могли бы рождаться в горячей Вселенной вскоре после Большого Взрыва при фазовом переходе, связанном со спонтанным нарушением симметрии и возникновением отличных от нуля однородных скалярных полей в вакууме. Количество рождающихся магнитных монополей определяется процессом развития Вселенной на ранней стадии, поэтому по их отсутствию в настоящее время можно судить об этом процессе. Одно из объяснений того, что реликтовые магнитные монополи не обнаружены, даётся теорией раздувающейся Вселенной (инфляции). Магнитные монополи ‘т Хоофта — Полякова обладают некоторыми необычными свойствами, благодаря которым их было бы легко обнаружить. В частности, взаимодействие с магнитным монополем может стимулировать распад нуклона, предсказываемый некоторыми моделями великого объединения^[6], то есть выступать в качестве катализатора такого распада.

Заряд магнитного монополя[править | править код]

Размерность заряда магнитного монополя совпадает с размерностью электрического заряда в системе СГС:

gD=cℏ2e=e2αE≈137e/2, {\displaystyle g_{D}={\frac {c\hbar }{2e}}={\frac {e}{2\alpha _{E}}}\approx 137e/2,\ }

где c{\displaystyle c} — скорость света в вакууме, ℏ{\displaystyle \hbar } — постоянная Планка и e{\displaystyle e} — элементарный заряд.

В системе СИ размерности магнитного и электрического зарядов различны (конвенция вебера):

gD=he, {\displaystyle g_{D}={\frac {h}{e}},\ }

где h{\displaystyle h} — постоянная Планка.

Конвенция ампер-метра (СИ):

gD=hc2ε0.{\displaystyle g_{D}={\frac {hc^{2}}{\varepsilon _{0}}}.}

Константа связи монополя[править | править код]

Известно, что электрические заряды имеют достаточно малую константу связи (т. н. постоянную тонкой структуры). В системе СГС она имеет следующее значение:

αE=e2cℏ≈1/137. {\displaystyle \alpha _{E}={\frac {e^{2}}{c\hbar }}\approx 1/137.\ }

В СИ мы имеем более громоздкое выражение:

αE=e22hcε0≈1/137, {\displaystyle \alpha _{E}={\frac {e^{2}}{2hc\varepsilon _{0}}}\approx 1/137,\ }

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная.

Аналогичным образом можно ввести и магнитную константу связи для системы СГС:

βE=gD2cℏ=14αE=34,25. {\displaystyle \beta _{E}={\frac {g_{D}^{2}}{c\hbar }}={\frac {1}{4\alpha _{E}}}=34{,}25.\ }

Для СИ имеет место выражение:

 — конвенция вебера:

βE=gD22hcμ0=14αE=34,25, {\displaystyle \beta _{E}={\frac {g_{D}^{2}}{2hc\mu _{0}}}={\frac {1}{4\alpha _{E}}}=34{,}25,\ }

 — конвенция ампер-метра:

βE=gD2μ02hc=14αE=34,25, {\displaystyle \beta _{E}={\frac {g_{D}^{2}\mu _{0}}{2hc}}={\frac {1}{4\alpha _{E}}}=34{,}25,\ }

где μ0{\displaystyle \mu _{0}} — магнитная постоянная вакуума. Здесь следует отметить, что магнитная константа значительно больше единицы и поэтому использование пертурбативных методов в квантовой электродинамике для магнитных зарядов не предоставляется возможным.

Масса монополя[править | править код]

Теория Дирака не предсказывает «массу магнитного монополя». Поэтому в настоящее время отсутствует единое мнение по оценке массы монополя (эксперимент только указывает на нижнюю границу). Здесь также можно отметить, что значение массы электрона является чисто экспериментальным фактом и не предсказывается стандартной моделью.

Нижняя оценка массы монополя[править | править код]

Нижнюю оценку для массы монополя можно оценить исходя из классического радиуса электрона (система СИ):

r0=e24πε0m0c2=αEλ02π, {\displaystyle r_{0}={\frac {e^{2}}{4\pi \varepsilon _{0}m_{0}c^{2}}}={\frac {\alpha _{E}\lambda _{0}}{2\pi }},\ }

где λ0{\displaystyle \lambda _{0}} — комптоновская длина волны электрона, m0{\displaystyle m_{0}} — масса электрона.

Аналогичным образом можно ввести значение для классического радиуса магнитного монополя (система СИ (конвенция вебера)):

rD0=gD24πμ0mDc2, {\displaystyle r_{D0}={\frac {g_{D}^{2}}{4\pi \mu _{0}m_{D}c^{2}}},\ }

где mD{\displaystyle m_{D}} — масса монополя. Таким образом, приравнивая классические радиусы, можно получить нижнюю оценку массы монополя:

mD=(gDe)2ε0μ0m0=14αEm0≈4692m0. {\displaystyle m_{D}=\left({\frac {g_{D}}{e}}\right)^{2}{\frac {\varepsilon _{0}}{\mu _{0}}}m_{0}={\frac {1}{4\alpha _{E}}}m_{0}\approx 4692m_{0}.\ }

Неоднократные попытки экспериментального обнаружения магнитного монополя не увенчались успехом. Особенно интенсивно поиски магнитного монополя космического происхождения проводились с начала 80-х годов XX века. Эксперименты можно разделить на несколько групп.

1. Магнитный монополь можно обнаружить непосредственно по связанному с ним магнитному потоку. Прохождение магнитного заряда ng0{\displaystyle ng_{0}} сквозь сверхпроводящий контур изменит поток на 2πΦ0{\displaystyle 2\pi \Phi _{0}}, где Φ0∼2⋅10−3Gm2{\displaystyle \Phi _{0}\sim 2\cdot 10^{-3}Gm^{2}} — квант магнитного потока, и явление электромагнитной индукции приведёт к с