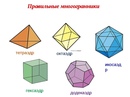
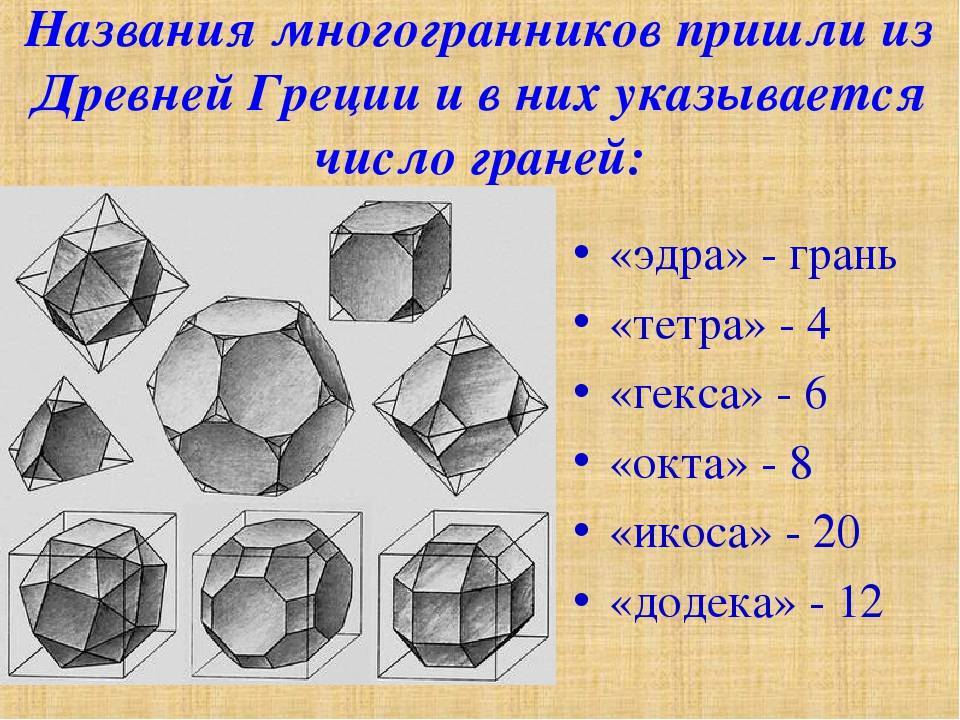
Основные геометрические фигуры

Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. Где же встречаются геометрические фигуры в нашей жизни?

Где встречаются геометрические фигуры в нашей жизни?

Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. 

Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

И в современном мире без этих знаний не прожить.

Где же встречаются геометрические фигуры в нашей жизни?

Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр. 

Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия. Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте. 

Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах. Кроме того, интерактивные задания красочные, интересные, увлекательные.

Итак,

Простейшие виды фигур

Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.

Точка

Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик. Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

Самыми простейшими фигурами являются луч и отрезок.

• ^{Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.}
• ^{Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.}

Линия

Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными. 

• ^{Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.}
• ^{Разомкнутая — когда начало и окончание линии не соединены.}
• ^{Прямая — непрерывная линия без изменений.}
• ^{Кривая — отличная от прямой линии.}
• ^{Ломаная — когда соединены отрезки не под углом 180 градусов.} 

Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости. 

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

Если все точки фигуры находятся в одной плоскости, значит, она является плоской. Плоские фигуры, которые знают все: точка, квадрат, прямоугольник, треугольник, круг, полукруг, окружность, овал, ромб, трапеция.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

 Есть три вида треугольников:

• ^{Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.}
• ^{Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.}
• ^{Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.}

Треугольники имеют следующие свойства:

• ^{в треугольнике напротив большего угла лежит большая сторона и наоборот;}
• ^{сумма углов треугольника всегда равна 180 градусам;}
• ^{все углы равностороннего треугольника равны 60 градусам;}
• ^{в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).}

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии. 

 

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

‍

Прямоугольник

‍

Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

• ^{противоположные стороны равны между собой;}
• ^{диагонали равны и делятся в точке пересечения пополам;}
• ^{около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.}

‍

Квадрат

Квадрат — это тот же прямоугольник, у которого:

• ^{все стороны равны;}
• ^{все углы равны и составляют 90 градусов;}
• ^{диагонали равны и перпендикулярны;}
• ^{центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.}

‍

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность. 

‍

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

• ^{противоположные стороны и углы равны;}
• ^{сумма двух любых соседних углов равна 180 градусам;}
• ^{диагонали пересекаются и точкой пересечения делятся пополам;}
• ^{каждая диагональ делит фигуру на два равных треугольника.}

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь. 

‍

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм², см², м², км² и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

• ^{Квадрат: периметр = 4 * сторона.}
• ^{Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.}
• ^{Неправильный многоугольник: периметр = сумме всех сторон многоугольника.}
• ^{Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).}

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

• ^{Параллелограмм: площадь = основание * высота}
• ^{Квадрат: площадь = сторона 1 * сторона 2}
• ^{Треугольник: площадь = ½ * основание * высота}
• ^{Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).}

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

• ^{интерактивные задания больше похожи на игру;}
• ^{их можно отрабатывать многократно и они не будут повторяться;}
• ^{платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;}
• ^{достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.}

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Геометрические фигуры для срисовки — 99 фото

Необычные геометрические фигуры

Интересные фигуры

Геометрические фигуры карандашом

Необычные геометрические фигуры

Треугольник Пенроуза Эшер

Узоры из прямых линий

Тату эскизы треугольник

Тату геометрические фигуры эскизы

Звезда дотворк

Необычные геометрические фигуры

Геометрические рисунки

Животные геометрическими фигурами

Сложные геометрические фигуры

Симметрия геометрических фигур

Развертка многогранника Эшера

Интересные фигуры

Узоры для рисования по клеткам

Сложные гиометрически ефигуранты

Геометрические рисунки простые

Необычные геометрические фиг

Необычные геометрические фигуры

Геометрические тату эскизы

Геометрическое рисование

Олень лайнворк

Кристалл скетч

Интересные геометрические фигуры

Геометрические тату эскизы

Треугольник Пенроуза Эшер

Тату геометрия эскизы

Фигуры из прямых линий

Геометрическая лиса

Геометрические Фракталы

Геометрический стиль рисования

Рисунки по клеточкам в тетради ручкой

Животные геометрическими фигурами

Красивые геометрические фигуры

Перспектива из геометрических фигур

Урок рисования натюрморта из геометрических тел

Необычные фигуры в геометрии

Легкие геометрические фигуры

Лёгкие узоры по клеточкам

Журавлик тату эскиз

Животные из геометричскихфигур

Геометрические животные простые

Графические фигуры

Единорог из геометрических фигур

Геометрические рисунки

Геометрический абстракционизм

Олень лайнворк

Объемные фигуры по клеточкам

Нестандартные геометрические фигуры

Геометрические рисунки тату

Геометрическая голова волка

Интересные геометрические рисунки

Необычные геометрические фигуры

Графические фигуры

Композиция из объемных геометрических фигур

Геометрические узоры Эшера

Раскраска бриллиант

Невозможные геометрические фигуры

Фигуры в перспективе карандашом

Треугольник карандашом

Геометрический абстракционизм

Объемные фигуры на бумаге

Несложные геометрические рисунки

Портрет линиями

Сакральная геометрия трилистник

Иллюзии карандашом

Раскраска драгоценные камни

Рисование объемных фигур

Мауриц Эшер правильные многогранники картина

Сердце геометрия эскиз

Алмаз рисунок

Рисунки ручкой в тетради

Необычные геометрические фигуры

Геометрические фигуры для рисования

Композиция и перспектива

Геометрия эскизы

Узор из кругов и треугольников

Геометрическое рисование

Сложные фигуры

Геометрические цветы

Нестандартные геометрические фигуры

Перспектива Графика

Линейно-конструктивный рисунок геометрических тел

Штриховка геометрических фигур композиция

Kerby Rosanes геометрические животные

Три пересекающиеся плоскости Эшер

Невозможная фигура звезда

Рисунки в стиле кубизм

Объемные фигуры по клеточкам

Красивые геометрические фигуры

Идеи для геометрических рисунков

Сердце геометрия

Сложные геометрические формы

Несложные геометрические рисунки

Геометрические фигуры по клеточкам сложные

Роджер Пенроуз треугольник

Рисование треугольниками

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

11 крутых форм, о которых вы не знали

Будь то природа, архитектура или продукты, которые мы используем, крутые формы окружают нас повсюду.

На самом деле формы образуют строительные блоки любого дизайна. И хотя мы можем этого не осознавать, каждая форма может заставить нас чувствовать себя определенным образом.

Бренды и визуальные коммуникаторы во всем мире могут использовать формы в дизайне, чтобы делиться определенными ценностями и сообщениями со своей аудиторией. Формы можно использовать в фирменном стиле, например, в логотипах, дизайне веб-сайтов и визитных карточек, или в дизайне продуктов для практических или эмоциональных целей.

Вот небольшая подборка из 8 крутых форм, которые можно использовать при редактировании, публикации и загрузке маркетингового контента с помощью Visme. Подробнее см. ниже:

Но формы не ограничиваются только кругами, квадратами и треугольниками. Есть несколько интересных форм, о которых вы, вероятно, не знали в школе. И, как и все другие формы и символы в мире, эти крутые формы также имеют свои собственные значения и эмоции.

Вот 11 классных форм, которые помогут вам создать осмысленный дизайн и лучше общаться со своей аудиторией.

Вы можете просмотреть визуальную инфографику этого сообщения ниже или пропустить вперед, чтобы прочитать подробное объяснение и историю каждой классной формы.

наш браузер не поддерживает тег видео.

Хотите создать собственную привлекательную инфографику?

• Доступ к сотням готовых к использованию шаблонов
• Добавьте тысячи бесплатных фигур, значков и многого другого
• Настройте все и вся под свой бренд

Зарегистрироваться. Это бесплатно.

 

11 прикольных форм, о которых вы не знали

1 Гептаграмма

Гептаграмма представляет собой семиконечную звезду, нарисованную семью прямыми штрихами.

Он использовался в различных религиях мира для обозначения чего-то священного. Например, в христианстве эта форма использовалась для обозначения семи дней творения.

Это также был символ богини Бабалон в Телеме.

Однако совсем недавно форма в значительной степени ассоциировалась с религией Викка — современной религией, основанной на древних традициях колдовства. Для виккан, которые поклоняются природе и следуют традициям фейри, гептаграмма является священным символом и известна как эльфийская звезда или звезда фейри.

Источник изображения

Помимо религии, гептаграмма также используется в алхимии; семиконечная звезда, которая относится к семи планетам, известным древним алхимикам.

С такой яркой историей гептаграмма, безусловно, является формой, которую вы не можете игнорировать.

Гептаграмму также можно увидеть на флагах разных стран, особенно на флагах Австралии и Иордании. Он также используется в логотипе Maersk, известной транспортно-логистической компании.

Источник изображения

Говорят, что Питер Мерск Мёллер, основатель Maersk, был глубоко религиозным христианином. После того, как его жена выздоровела от болезни, он прикрепил к своему пароходу «Лаура» синее знамя с белой семиконечной звездой — гептаграммой, которое впоследствии стало эмблемой Maersk Group.

В письме жене в 1886 году Петр объяснял: «Звездочка на дымоходе — это воспоминание о той ночи, когда я молился за тебя и просил знамения: Если на сером и облачном небе появится звезда, это означало бы, что Господь отвечает на молитвы».

Визуальные коммуникаторы могут использовать эту классную форму, чтобы показать совершенство или создать глубокое чувство принадлежности к своей аудитории. Компании могут использовать гептаграмму в своих проектах, чтобы проиллюстрировать различные разделы, отделы или основные ценности.

 

2 Triquetra

Буквальное значение слова triquetra — «треугольный».

Эта классная треугольная форма симметрична и образована перекрытием трех дуг. В истории он использовался для различных целей, особенно в религии.

В христианстве три края трикетры представляют Святую Троицу Отца, Сына и Святого Духа. Вот почему эту форму также называют «узлом Троицы».

Трикетра часто изображается в виде круга — круга Троицы — вплетенного между тремя дугами, что символизирует единство. Форма также появляется в кельтском и раннехристианском искусстве.

Источник изображения

Выше показано, как трикетра используется в оформлении окон католической церкви Непорочного Сердца Марии в Уилмингтоне, Делавэр.

Трикетра также появляется в американском сериале «Зачарованные».

Хотя в сериале рассказывалось о трех ведьмах, сражающихся с демонами и колдунами, никакого религиозного значения трикетра не подразумевалось.

Источник изображения

Трикетра — отличная форма для использования в визуальном дизайне и брендинге для всех типов визуальных коммуникаторов. Его можно использовать для иллюстрации объединения трех элементов, таких как ценности, личности или другие аспекты.

 

3 Звезда Лакшми

Звезда Лакшми — это особая октаграмма — восьмиугольник, состоящий из двух конгруэнтных квадратов с одним и тем же центром, расположенным под углом 45°.

Происхождение этой прикольной формы восходит к индуистской религии.

В индуизме Лакшми — богиня богатства — имеет восемь форм проявления, известных как Ашталакшми. Они представлены двумя переплетенными квадратами, образующими октаграмму.

Каждое воплощение представляет определенную форму богатства: деньги, способность к транспорту, бесконечное процветание, победу, терпение, здоровье и питание, знания и семью.

Эта прикольная форма также используется в центральном вестибюле здания парламента в Лондоне.

Сегодня эта форма чаще встречается в архитектурном дизайне, коврах, плитке, ювелирных изделиях и других украшениях.

Он даже есть на сайте американской рок-группы Faith No More.

Источник изображения

Звезда Лакшми, безусловно, имеет очень уникальную форму с глубоким символизмом. Это отличный выбор для духовных и исцеляющих брендов, стремящихся создать новую идентичность бренда.

 

4 Лемниската

Лемниската выглядит как кривая в виде восьмерки и напоминает символ бесконечности.

Происхождение лемнискаты восходит к 5 веку нашей эры. Он был найден греческим философом-неоплатоником Проклом, который назвал эту форму конскими путами, поскольку она напоминала два соединенных вместе копыта.

В графическом дизайне эта крутая форма часто используется в типографике. Взгляните на логотип Coursera, известной онлайн-платформы для обучения.

Источник изображения

Символ бесконечности символизирует непрерывность и бессмертие. В случае с Coursera выше, он явно используется для того, чтобы показать, что обучение и рост — это бесконечный процесс.

Предстоящий чемпионат мира по футболу FIFA 2022 также использует форму лемнискаты в своем официальном логотипе.

 

 

Источник изображения

 

5 Vesica Piscis

Vesica Piscis очень похожа на диаграмму Венна, но имеет гораздо более глубокое значение.

Эта крутая форма образована путем пересечения двух кругов одинакового радиуса, где центр каждого круга лежит на окружности другого.

Дословный перевод Vesica Piscis — «рыбий пузырь». Он считается священной фигурой, потому что отношение его ширины к высоте составляет 165:153 или 1,73203, что считается священным числом.

Один из витражей церкви Святой Марии и Всех Святых в Честерфилде демонстрирует Vesica Piscis, созданную еще в 1947.

Источник изображения

Эту крутую фигуру можно также увидеть в Колодце Чаши в графстве Сомерсет, Англия.

Vesica Piscis также используется в современном ювелирном дизайне. Многие организации по всему миру так или иначе использовали эту форму.

Mastercard, одна из самых известных в мире финансовых компаний, использует эту прикольную форму в своем логотипе.

Источник изображения

Причина, по которой Vesica Piscis была использована в их логотипе, может заключаться в том, что Mastercard была сформирована из союза многих различных банков и финансовых учреждений.

Они также придумали слоган «Mastercard, сердце коммерции». в 2006 году, что делает логотип похожим на символ центрального источника энергии, такого как сердце.

Визуальные коммуникаторы и бренды могут использовать эту форму для обозначения союза двух сил или источника. Его также можно использовать для обозначения созидания, рождения и плодородия, поскольку он напоминает женский репродуктивный орган.

 

6 Треугольник Рело

Треугольник Рело (произносится как «ру-лос») представляет собой криволинейный треугольник, образованный пересечением трех круговых дисков.

Вы, наверное, видели эту крутую форму в гитарных медиаторах, карандашах, архитектуре, монетах и ​​даже сверлах.

Треугольник Рело назван в честь немецкого инженера 19-го века Франца Рело, который был известен тем, что использовал эту схему в своей работе.

Вы также можете найти эту форму в корпоративных логотипах и вывесках по всему миру. Например, Национальная система маршрутов и Система велосипедных маршрутов США отмечают маршруты треугольниками Рело на своих указателях.

Источник изображения

Эта форма также использовалась в архитектуре, например, в этой башне в Барселоне, в которой использовался треугольник Рело для создания конструкции, которая одновременно легкая и максимально увеличивает пространство.

Источник изображения

 

7 Эннеаграмма

Эннеаграмма (произносится как «а-а-грамм») представляет собой девятистороннюю фигуру, обычно заключенную в круг.

Если эта классная форма кажется вам знакомой, вы, вероятно, являетесь поклонником Slipknot.

Источник изображения

Происхождение этой классной формы неясно. Некоторые говорят, что его можно проследить до сакральной геометрии математиков-пифагорейцев, в то время как другие считают, что он мог войти в иудаизм и представляет Древо Жизни в Каббале.

Чаще всего эннеаграмма используется в системе анализа для представления спектра возможных типов личности, где числа 1-9 используются для представления части личности. Вы можете пройти тест здесь.

Источник изображения

В визуальной идентификации вы можете использовать эннеаграмму для описания нескольких личностей или аспектов вашего бренда.

 

8 Нонагон

Нонагон, также известный как эннеагон, представляет собой многоугольник с девятью сторонами.

Все стороны правильного многоугольника имеют одинаковую длину, а углы равны 140 градусам. Однако неправильный девятиугольник не имеет равных сторон или углов.

Эту крутую форму можно увидеть в различных зданиях по всему миру. Например, вершина здания US Steel Building в Питтсбурге, штат Пенсильвания, представляет собой неправильный девятиугольник.

Источник изображения

Он выглядит как треугольник, но на самом деле у него девять сторон. Иди и посчитай их.

Эта прикольная форма также связана с религией Веры Бахаи — все их Молитвенные дома должны иметь девять сторон. Вот видео, в котором показана коллекция храмов бахаи мира.

 

У фигуры даже есть своя детская песенка. Так круто!

Нонагон также широко используется в дизайне интерьера, дизайне ювелирных изделий, искусстве и даже в брендинге и логотипах. Поскольку число 9 считается священным в большинстве религий, эта форма идеально подходит для символа магии, силы и мудрости в ваших замыслах.

 

9 Кольцо

Кольцо напоминает кольцеобразный объект, центральная часть которого окружена двумя концентрическими окружностями. Эта крутая форма обычно используется при строительстве нефтяных и водяных скважин, насосно-компрессорных труб и обсадных труб.

Помимо использования в производстве и архитектуре, эта крутая форма также может быть использована в фирменном стиле, корпоративных презентациях, рекламных презентациях и даже логотипах, чтобы представить цель, цель или направление вашего бизнеса.

Кольцо также используется в логотипе Target, восьмого по величине розничного продавца в США.

Источник изображения

 

10 Лента Мебиуса

Лента Мебиуса или лента Мебиуса представляет собой трехмерную фигуру с одной сплошной стороной.

Эта форма названа в честь Августа Фердинанда Мёбиуса, немецкого математика, который также был поклонником необычных форм.

Вы, должно быть, видели эту фигуру как символ переработки.

Источник изображения

Лента Мёбиуса символизирует непрерывность, что объясняет, почему она используется в качестве общепринятого символа вторичной переработки.

Это также символ инноваций и постоянных изменений, поэтому он также используется в логотипе Google Диска.

Источник изображения

Ленту Мёбиуса можно использовать для передачи различных ценностей и эмоций. Эту крутую форму также можно использовать для представления единства, баланса, реинкарнации и других подобных значений в ваших проектах.

Эту форму часто можно увидеть на обручальных кольцах, символизирующих бесконечность и вечную любовь. Он также используется дизайнером продукта Арихиро Мияке в его подвесной лампе Kepler.

Источник изображения

 

11 Squircle

Squircle — это уникальная форма, которая находится где-то между квадратом и кругом.

Может показаться, что это не так, но эта милая фигурка на самом деле имеет математическое происхождение. Его обычно можно увидеть в дизайне обеденных тарелок, оптики, монет и многого другого.

Даже в старых телефонах Nokia в сенсорных панелях был встроен сквиркл.

Эту классную форму теперь можно найти на значках приложений вашего iPhone, а также на задней панели iPhone 11 Pro Max от Apple.

Источник изображения

Несколько лет назад квадраты были в моде в автомобильном дизайне. Его можно было найти буквально везде — от фар до салона.

Одна из причин, по которой сквиркл так популярен, заключается в его практичности, а также в элегантности и утонченности. Квадратная тарелка, например, может вместить больше еды, чем круглая или квадратная тарелка.

Бьюсь об заклад, вы никогда этого не понимали, но даже Instagram использует сквиркл в качестве своего логотипа!

Источник изображения

Как бренд или визуальный коммуникатор, вы можете использовать квадрат, чтобы символизировать инновации и креативность в ваших проектах. Этот символизм проистекает из того, как эта крутая форма плавно объединяет две обычные формы, чтобы создать более красивую и функциональную.

 

Создавайте уникальные дизайны с помощью этих крутых форм

Каждый хороший визуальный коммуникатор должен знать «почему» за использованием определенного символа или формы в своих проектах. Это поможет вам создавать не только более красивые дизайны, но и мощные и эффективные.

Использование классных креативных форм может превратить скучный или простой дизайн в осмысленные визуальные эффекты, которые найдут отклик у вашей аудитории и сделают ее ближе к вашему бренду.

Начните использовать эти классные формы в своих проектах, чтобы сформировать уникальные и запоминающиеся ассоциации с вашим брендом. В Visme вы можете создавать всевозможные визуальные эффекты, такие как инфографика, изображения для социальных сетей, презентации, фирменный стиль и многое другое.

Зарегистрируйте бесплатную учетную запись прямо сейчас и протестируйте ее!

Удивительный список 2D и 3D фигур на английском языке • 7ESL

Все, что мы можем видеть в этом мире, состоит из различных геометрических фигур. Черт возьми, даже планета, на которой мы живем, представляет собой одну большую геометрическую форму, если мы посмотрим на нее из космоса. Следовательно, важно знать большинство из них не только для того, чтобы знать, что они из себя представляют, но и для нашего образования, поскольку геометрические фигуры играют важную роль в различных областях, таких как естественные науки и математика. В связи с этим мы сделали эту статью, чтобы кратко объяснить, что такое геометрические фигуры, а также их множество различных типов, как двумерных (2D), так и трехмерных (3D).

Содержание

Что такое геометрическая фигура?

По определению, геометрические фигуры представляют собой наиболее чистую форму объекта или фигуры в том смысле, что независимо от того, насколько сильно они перемещаются, вращаются, увеличиваются или отражают в зеркале, они просто останутся в той же форме, что и были изначально когда вы еще не трогали его. Говоря еще проще, если вы скажете, что что-то является кругом в геометрии, независимо от того, под каким углом вы на это смотрите или сколько вы с этим возитесь, оно все равно будет иметь свойство геометрического круга.

С зарождением геометрии математики начали устанавливать правила того, что составляет определенную геометрическую форму, и эти правила определили различные типы геометрических фигур, которые мы имеем сегодня.

Геометрические фигуры

Для упрощения геометрические фигуры разделены на две основные группы в зависимости от их размеров. Первая группа состоит из двухмерных (2D) форм, которые имеют длину и ширину, а вторая группа состоит из трехмерных (3D) форм, которые имеют длину, ширину и глубину.

Двухмерные геометрические фигуры

Как было сказано выше, двухмерные геометрические фигуры имеют длину и ширину. В 2D-формах есть еще две классификации, а именно многоугольники и не-полигоны. Многоугольники — это двумерные геометрические фигуры, состоящие из прямых линий, которые встречаются в одной из своих конечных точек и образуют замкнутую фигуру. Неполигоны, с другой стороны, представляют собой замкнутые фигуры, состоящие из изогнутых линий или комбинации прямых и изогнутых линий.

1. Треугольники

Треугольник — это тип многоугольника, который имеет ровно три стороны и три вершины или угла. Существуют различные виды треугольников, и они классифицируются по длине сторон или по внутренним углам.

Типы треугольников по длинам сторон

A. Равносторонний треугольник

Это разновидность треугольника, у которого все три стороны имеют одинаковую длину.

Штифт

B. Равнобедренный треугольник

Это вид треугольника, у которого ровно две стороны одинаковой длины.

Штифт

C. Разносторонний треугольник

Это вид треугольника, у которого нет сторон одинаковой длины.

Штифт

Типы треугольников по внутренним углам

A. Прямоугольный треугольник

Треугольник с внутренним углом 90 градусов. Сторона, прямо противоположная этому углу, называется гипотенузой, которая также является самой длинной стороной прямоугольного треугольника.

Шпилька

B. Косой треугольник

Это просто треугольник, внутренний угол которого не равен 90 градусов. Под косыми треугольниками находятся еще два вида а именно:

B.1. Остроугольный треугольник

Три внутренних угла этих треугольников меньше 90 градусов.

Штифт

B.2. Тупоугольный треугольник

У этих треугольников один внутренний угол больше 90 градусов.

Pin

C. Вырожденный треугольник

Это треугольник, внутренний угол которого равен 180 градусам. Однако технически он выглядит как отрезок линии, если вы попытаетесь его нарисовать.

Штифт

2. Четырехугольники

Четырехугольники — это многоугольники, имеющие ровно четыре стороны и четыре угла. Четырехугольники делятся на два основных типа, а именно, простые и сложные.

A. Простой четырехугольник

Простые четырехугольники — это четырехугольники, которые сами по себе не пересекаются. Этот тип далее делится на два, а именно:

А.1. Выпуклые четырехугольники  — Все четырехугольники, принадлежащие к этому типу, не имеют внутреннего угла более 180 градусов. Существуют следующие его типы:

A1.1. Трапеция

Четырехугольник, стороны которого не параллельны друг другу.

Штифт

A1.2. Трапеция

Четырехугольник, у которого ровно одна пара параллельных сторон.

Штифт

A1.3. Равнобедренная трапеция

Трапеция, у которой углы при основании равны.

Штифт

A1.4. Параллелограмм

Четырехугольник с двумя парами параллельных сторон.

Штифт

A1.5. Ромб

Четырехугольник с четырьмя равными сторонами.

Штифт

A1.6. Квадрат

Тип ромба с четырьмя прямыми углами.

Штифт

A1.7. Прямоугольник

Тип параллелограмма со всеми внутренними углами, равными 90 градусов.

Штифт

A1.8. Воздушный змей

Четырехугольник, у которого смежные стороны равны.

Штифт

А.2. Вогнутые четырехугольники

Четырехугольник с внутренним углом больше 180 градусов. Он имеет только один тип, который называется дротик.

Булавка

B. Сложный четырехугольник

Эти четырехугольники пересекаются сами по себе, что делает его похожим на простую форму галстука-бабочки.

Штифт

3. Вогнутые и выпуклые многоугольники

Основное различие между вогнутыми и выпуклыми многоугольниками заключается в измерении их внутренних углов. Просто у выпуклого многоугольника все внутренние углы меньше 180 градусов, а у вогнутого многоугольника один или несколько внутренних углов выходят за пределы 180 градусов.

3.1. Выпуклый многоугольник

Штифт

3.2. Вогнутый многоугольник

Штифт

4. Правильные и неправильные многоугольники

Это две другие классификации многоугольника, в которых правильные многоугольники имеют стороны одинаковой длины и внутренние углы одинаковой величины. Наиболее распространенные примеры правильного многоугольника включают равносторонний треугольник, квадрат, пятиугольник, шестиугольники и восьмиугольники. С другой стороны, неправильные многоугольники — это фигуры, которые не удовлетворяют обоим условиям, чтобы считаться правильным многоугольником.

4.1. Правильные многоугольники

Штифт

4.2. Неправильные многоугольники

Штифт

5. Кривые 2D-фигуры

Как следует из названия, изогнутые 2D-фигуры представляют собой замкнутые фигуры, образованные чисто изогнутыми линиями или комбинацией прямых и кривых линий. Как обсуждалось ранее, все изогнутые 2D-формы также считаются не многоугольниками. Наиболее распространенными примерами таких геометрических фигур являются круги, эллипсы, дуги, сектора, сегменты, параболы и гиперболы.

5.1. Круг

Штифт

5.2. Эллипс

Штифт

5.3. Сектора

Пин

5.4. Парабола

Штифт

5.5. Гипербола

Булавка

Трехмерные геометрические фигуры

Как упоминалось ранее, трехмерные (трехмерные) фигуры, также известные как объемные фигуры, представляют собой фигуры, которые имеют длину, ширину и дополнительное измерение, называемое глубиной. С математической точки зрения сплошных фигур много, но основные типы следующие:

1. Прямоугольный куб

Этот тип объемной фигуры имеет шесть граней в форме прямоугольника. Каждая смежная сторона его грани встречается и образует точный угол в 90 градусов.

Штифт

2. Параллелепипед

Эта фигура похожа на прямоугольный куб, за исключением того, что его грани представляют собой параллелограммы, а не прямоугольники. Следовательно, его смежные грани не образуют углов 90 градусов.

Шпилька

3. Ромбоэдр

Эта фигура представляет собой параллелепипед, все ребра которого имеют одинаковую длину.

Булавка

4. Многогранник

Это любые объемные фигуры, которые имеют плоские многоугольные грани, а также острые углы и прямые края.

Шпилька

5. Призма

Это объемные фигуры, имеющие два основания одинакового размера, соединенные одинаковыми гранями, строго параллелограммными. Количество граней соответствует количеству сторон, которые имеют основания.

Штифт

6. Конус

Объемная фигура с круглым основанием, которое плавно сужается к точке, называемой вершиной.

Штифт

7. Цилиндр

Цилиндр представляет собой объемную фигуру с двумя круглыми основаниями вверху и внизу. Его стороны параллельны друг другу, а его поперечное сечение может быть как кругом, так и овалом, в зависимости от огранки.

Штифт

8. Эллипсоид

Эта фигура получается путем вращения эллипса вокруг своих осей.

Булавка

9. Лимон

Эта фигура получается путем вращения дуги окружности вокруг ее большой оси.

Штифт

10. Гиперболоид

Эта объемная фигура получается при вращении гиперболы вокруг одной из ее главных осей.

Штифт

11. Платоновы тела

Эти тела представляют собой правильные выпуклые многогранники, каждая из граней которых является правильным многоугольником. В геометрии этим критериям удовлетворяют только пять объемных фигур, а именно:

11.1. Тетраэдр

Четыре грани

Штифт

11.2. Куб

Шесть граней

Штифт

11.3. Октаэдр

Восьмигранник

Штифт

11.4. Додекаэдр

Двенадцать граней

Штифт

11.