Прямоугольник — Википедия

Материал из Википедии — свободной энциклопедии

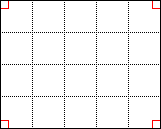
Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам).

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует.

• Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны.
• Стороны прямоугольника являются его высотами.
• Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).
• Около любого прямоугольника можно описать окружность, причём диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).

• Длиной прямоугольника называют длину более длинной пары его сторон, а шириной — длину более короткой пары сторон.
• Величина площади прямоугольника равна произведению ширины прямоугольника на его длину.
• Периметр прямоугольника равен удвоенной сумме длин его ширины и длины.

• Длины диагоналей прямоугольника равны.
• Диагонали прямоугольника делятся точкой пересечения пополам.
• Длина диагонали прямоугольника вычисляется по теореме Пифагора и равна квадратному корню из суммы квадратов длины и ширины.

Параллелограмм является прямоугольником, если выполняется любое из условий:

• Если диагонали параллелограмма равны.
• Если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон.
• Если углы параллелограмма равны.

Прямоугольник. Свойства и признаки прямоугольника

Категория: Справочные материалы

Елена Репина 2013-07-26 2013-09-22

Прямоугольник — параллелограмм, у которого все углы прямые.

Частным случаем прямоугольника является квадрат.

Свойства прямоугольника 

1. Так как  прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.

 Помимо этого:

2. Стороны прямоугольника являются его высотами.

3. Диагонали прямоугольника равны.

4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.

5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.

Признаки параллелограмма

 

Параллелограмм является прямоугольником, если выполняется любое из условий:

1. Диагонали параллелограмма равны.

2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.

3.  Все углы параллелограмма равны.

Площадь прямоугольника

 

 

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Автор: egeMax | Нет комментариев

Что такое прямоугольник? Частные случаи прямоугольника

География, биология, химия, алгебра, геометрия… Школьникам приходится иметь дело с множеством сведений из самых различных наук. Однако есть области знаний, в которых достаточно просто разобраться, ознакомившись с их основными законами. К ним относится и геометрия. Чтобы познать все тонкости этой науки, надо обязательно познакомиться с ее азами, аксиомами. Ведь без основ в геометрии никуда.

Определение прямоугольника

Прямоугольник – это геометрическая фигура с четырьмя прямыми углами. Определение довольно простое, но не стоит думать, что у школьника не возникнет проблем с изучением такой темы, ведь здесь есть ряд особенностей. Размеры прямоугольника зависят от длины его сторон, которые наиболее часто обозначаются латинскими буквами а и b.

Свойства прямоугольника

• стороны, лежащие друга против друга, равны и параллельны;
• диагонали фигуры равны;
• точка пересечения диагоналей делит их пополам;
• прямоугольник можно поделить на два равных прямоугольных треугольника.

Признаки прямоугольника

Существует всего три признака, которыми обладает прямоугольник. Вот они:

• параллелограмм с равными диагоналями – это прямоугольник;
• параллелограмм с одним прямым углом – это прямоугольник;
• четырехугольник с тремя прямыми углами – это прямоугольник.

Еще немного интересного

Итак, что такое прямоугольник, теперь понятно, но какую роль он играет в геометрических задачах и при измерениях на практике, еще предстоит разобраться. Так, в первую очередь надо сказать, что это наиболее удобная геометрическая фигура, при помощи которой можно делить площадь на участки и на открытой местности, и в помещениях.

Что такое прямоугольник? Как известно, он является четырехугольником. Существует множество разновидностей последнего, среди которых можно назвать трапецию (только две стороны равны), параллелограмм (противоположные стороны параллельны), квадрат (все углы и стороны одинаковые), ромб (параллелограмм с равными сторонами) и другие. Частным же случаем прямоугольника является квадрат, у которого все углы прямые, а стороны равны.

Нельзя говорить о том, что такое прямоугольник, и не упомянуть о том, как же определить его размеры. Площадью этой геометрической фигуры принято считать произведение ее ширины на длину, а периметр же, как и у любой фигуры, равняется сумме длин всех сторон. В данном случае он также равен удвоенной сумме длины и ширины, поскольку противолежащие стороны прямоугольника равны. Теперь вы знаете, что такое прямоугольник и что с ним делать, решая задачи и постигая секреты такой загадочной и таинственной науки, как геометрия.

Прямоугольник

Давайте вспомним, что параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

Дадим определение прямоугольнику. Итак, прямоугольник – это параллелограмм, у которого все углы прямые.

Так как прямоугольник является параллелограммом, то он обладает всеми его свойствами.

У прямоугольника противоположные стороны равны.

Диагонали прямоугольника точкой пересечения делятся пополам.

Кроме этих свойств рассмотрим ещё одно свойство – свойство диагоналей прямоугольника.

Теорема. Свойство диагоналей прямоугольника. Диагонали прямоугольника равны.

Доказательство.

Рассмотрим прямоугольные  и .

Катет  – общий,  как противоположные стороны прямоугольника.

 по двум катетам.

Следовательно, .

Что и требовалось доказать.

Теорема. Признак прямоугольника. Если у параллелограмма диагонали равны, то этот параллелограмм – прямоугольник.

Доказательство.

 

Пусть  – параллелограмм,

.

Рассмотрим  и .

Сторона  – общая,  как противоположные стороны параллелограмма,

 по условию.

 по третьему признаку. Следовательно, .

, .

Получаем .

.

.

Следовательно,  – прямоугольник.

Теорема доказана.

Давайте решим задачу.

Задача. В прямоугольнике  сторона

 см, а. Найдите диагональ .

Решение.

 – прямоугольный.

.

 (см).

,следовательно,

 см.

Ответ:  см.

Задача. В прямоугольнике  диагонали пересекаются в точке . . Найдите .

Решение.

,

следовательно,  – равнобедренный.

.

,

,

,

,

.

Ответ:

.

Задача. Найдите периметр прямоугольника , если биссектриса  делит сторону  на отрезки  см и  см.

Решение.

 – прямоугольный.

.

,.

 – равнобедренный,.

Так как  см,  то  см.

 см.

 (см),

 см.

,

 (см).

Ответ:  см.

32 флага мира, которые явно придумали люди с фантазией (Хотя это не относится к Чаду)

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и

ВКонтакте

В мире насчитывается 197 признанных государств, и у каждого из них есть свой официальный флаг. Как одежда многое говорит о человеке, так и флаг может многое рассказать о своей стране.

AdMe.ru старательно изучил флаги со всего мира и нашел множество интересных совпадений, необычностей и занимательных фактов, о которых мы даже не подозревали. Начнем с того, что все государственные флаги в мире имеют прямоугольную форму. Кроме одного.

Непал — единственная страна в мире, чей флаг имеет столь необычные очертания. Два треугольника в основе флага символизируют две вершины Эвереста, которые находятся на границе этого государства. По легенде, Непал будет существовать, пока будут существовать луна и солнце, изображенные на флаге.

У всех остальных стран флаги имеют форму прямоугольника. Но среди них выделяются Ватикан и Швейцария — их флаги квадратные.

Красный крест, используемый Международным комитетом Красного Креста, происходит от швейцарского флага с цветами наоборот. Этот символ был выбран в честь основателя МККК швейцарца Анри Дюнана.

Самые многочисленные флаги — горизонтальные трехполосные. Таких флагов насчитывается 55.

Самые популярные цвета на флагах мировых держав — красный, белый и синий. Хотя бы один из них всегда будет присутствовать на флаге.

Вместе с тем Ямайка в День независимости от Великобритании, 6 августа 1962 года, приняла желто-черно-зеленый флаг. Эти цвета встречаются намного реже.

Самый редкий цвет, встречающийся на государственном флаге, — фиолетовый. Это связано с тем, что добывать натуральный фиолетовый краситель раньше было сложно и дорого, а к моменту, когда в конце XIX века появился искусственный, большинство стран уже определилось с цветами на собственных флагах.

Сегодня фиолетовый цвет можно увидеть лишь на флаге Содружества Доминики. Он украшает грудь попугая сиссеру — символ этого островного государства.

Еще один редкий цвет, присутствующий лишь на одном государственном флаге, — аквамариновый. Он обозначает воду на флаге Багамских Островов. Желтая полоса — это берег, а черный треугольник символизирует единство и решимость багамцев.

Этот флаг сравнительно молод, ему 45 лет. Он был принят в 1973 году.

Теорема Пифагора — Википедия

Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость^[⇨]

Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида^[⇨].

Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение^[⇨]: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.

Существует ряд обобщений данной теоремы^[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется^[⇨].

По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок»^[1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы^[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

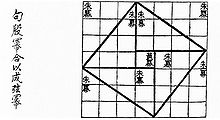
В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы^[3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.

Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки^[⇨][4], но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако когда такие авторы, как Плутарх и Цицерон, пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненно^[5][6]. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков^[7].

Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора^[8].

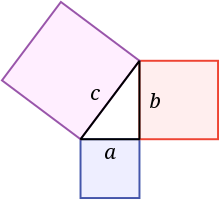Сумма площадей квадратов, опирающихся на катеты a{\displaystyle a} и b{\displaystyle b}, равна площади квадрата, построенного на гипотенузе c{\displaystyle c}

Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны a{\displaystyle a} и b{\displaystyle b}, а длина гипотенузы — c{\displaystyle c}, выполнено соотношение:

a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}.

Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.

Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}. Как следствие, для всякой тройки положительных чисел a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}, такой, что a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}, существует прямоугольный треугольник с катетами a{\displaystyle a} и b{\displaystyle b} и гипотенузой c{\displaystyle c}.

В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора^[9], что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия^[⇨]), метод площадей^[⇨], существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники[править | править код]

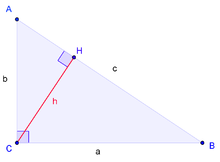
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры. В нём для треугольника △ABC{\displaystyle \triangle ABC} с прямым углом при вершине C{\displaystyle C} со сторонами a,b,c{\displaystyle a,b,c}, противолежащими вершинам A,B,C{\displaystyle A,B,C} соответственно, проводится высота CH{\displaystyle CH}, при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: △ABC∼△ACH{\displaystyle \triangle ABC\sim \triangle ACH} и △ABC∼△CBH{\displaystyle \triangle ABC\sim \triangle CBH}, из чего непосредственно следуют соотношения:

ac=|HB|a{\displaystyle {\frac {a}{c}}={\frac {|HB|}{a}}}; bc=|AH|b{\displaystyle {\frac {b}{c}}={\frac {|AH|}{b}}}.

При перемножении крайних членов пропорций выводятся равенства:

a2=c⋅|HB|{\displaystyle a^{2}=c\cdot |HB|}; b2=c⋅|AH|{\displaystyle b^{2}=c\cdot |AH|},

покомпонентное сложение которых даёт требуемый результат:

a2+b2=c⋅(|HB|+|AH|)=c2⇔a2+b2=c2{\displaystyle a^{2}+b^{2}=c\cdot \left(|HB|+|AH|\right)=c^{2}\,\Leftrightarrow \,a^{2}+b^{2}=c^{2}}.

Доказательства методом площадей[править | править код]

Большое число доказательств задействуют понятие площади. Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость[править | править код]

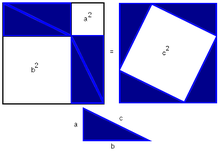Схема доказательства через равнодополняемость.

Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами a,b{\displaystyle a,b} и гипотенузой c{\displaystyle c}, расположенные таким образом, чтобы образовывать квадрат со стороной a+b{\displaystyle a+b} и внутренний четырёхугольник со сторонами длиной c{\displaystyle c}. Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна (a+b)2{\displaystyle (a+b)^{2}}, он состоит из внутреннего квадрата площадью c2{\displaystyle c^{2}} и четырёх прямоугольных треугольников, каждый площадью ab2{\displaystyle {\frac {ab}{2}}}, в результате из соотношения (a+b)2=4⋅ab2+c2{\displaystyle (a+b)^{2}=4\cdot {\frac {ab}{2}}+c^{2}} при алгебраическом преобразовании следует утверждение теоремы.

Доказательство Евклида[править | править код]

Чертёж к доказательству Евклида. Основное направление доказательства — установление конгруэнтности △ACK≅△ABD{\displaystyle \triangle ACK\cong \triangle ABD}, площадь которых составляет половину площади прямоугольников AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} соответственно.

Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.

Конструкция, используемая для доказательства следующая: для прямоугольного треугольника △ABC{\displaystyle \triangle ABC} с прямым углом C{\displaystyle C}, квадратов над катетами ACED{\displaystyle ACED} и BCFG{\displaystyle BCFG} и квадрата над гипотенузой ABIK{\displaystyle ABIK} строится высота CH{\displaystyle CH} и продолжающий её луч s{\displaystyle s}, разбивающий квадрат над гипотенузой на два прямоугольника AHJK{\displaystyle AHJK} и BHJI{\displaystyle BHJI}. Доказательство нацелено на установление равенства площадей прямоугольника AHJK{\displaystyle AHJK} с квадратом над катетом AC{\displaystyle AC}; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.

Равенство площадей прямоугольника AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} устанавливается через конгруэнтность треугольников △ACK{\displaystyle \triangle ACK} и △ABD{\displaystyle \triangle ABD}, площадь каждого из которых равна половине площади прямоугольников AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямого угла и угла при A{\displaystyle A}.

Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников AHJK{\displaystyle AHJK} и BHJI{\displaystyle BHJI}, равна сумме площадей квадратов над катетами.

Доказательство Леонардо да Винчи[править | править код]

Чертёж к доказательству Леонардо да Винчи

К методу площадей относится также доказательство, найденное Леонардо да Винчи. Пусть дан прямоугольный треугольник △ABC{\displaystyle \triangle ABC} с прямым углом C{\displaystyle C} и квадраты ACED{\displaystyle ACED}, BCFG{\displaystyle BCFG} и ABHJ{\displaystyle ABHJ} (см. рисунок). В этом доказательстве на стороне HJ{\displaystyle HJ} последнего во внешнюю сторону строится треугольник, конгруэнтный △ABC{\displaystyle \triangle ABC}, притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть JI=BC{\displaystyle JI=BC} и HI=AC{\displaystyle HI=AC}). Прямая CI{\displaystyle CI} разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники △ABC{\displaystyle \triangle ABC} и △JHI{\displaystyle \triangle JHI} равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников CAJI{\displaystyle CAJI} и DABG{\displaystyle DABG}, площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.

Через площади подобных треугольников[править | править код]

Следующее доказательство основано на том, что площади подобных треугольников относятся как квадраты соответственных сторон.

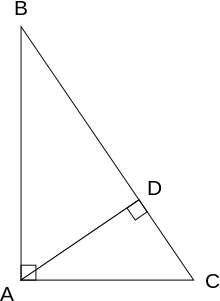
Пусть ABC{\displaystyle ABC} есть прямоугольный треугольник, AD{\displaystyle AD} — перпендикуляр, опущенный на гипотенузу из вершины прямого угла. Треугольники ABC{\displaystyle ABC}, DBA{\displaystyle DBA} подобны, так как имеют по прямому углу и ещё общий угол B{\displaystyle B}. Значит

площадь DBAплощадь ABC=AB2BC2.{\displaystyle {\frac {{\text{площадь}}~DBA}{{\text{площадь}}~ABC}}={\frac {AB^{2}}{BC^{2}}}.}

Точно также получаем, что

площадь DACплощадь ABC=AC2BC2.{\displaystyle {\frac {{\text{площадь}}~DAC}{{\text{площадь}}~ABC}}={\frac {AC^{2}}{BC^{2}}}.}

Поскольку треугольники DBA{\displaystyle DBA} и DAC{\displaystyle DAC} вместе составляют △ABC{\displaystyle \triangle ABC}, сумма площадей △DBA{\displaystyle \triangle DBA} и △DAC{\displaystyle \triangle DAC} равна площади △ABC{\displaystyle \triangle ABC}. Отсюда

AB2+AC2BC2=1{\displaystyle {\frac {AB^{2}+AC^{2}}{BC^{2}}}=1}

или AB2+AC2=BC2.{\displaystyle AB^{2}+AC^{2}=BC^{2}.}

Доказательство методом бесконечно малых[править | править код]

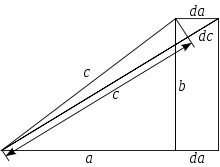Доказательство методом бесконечно малых

Существует несколько доказательств, прибегающих к технике дифференциальных уравнений. В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов a{\displaystyle a} и b{\displaystyle b} и гипотенузы c{\displaystyle c}. Например, приращение катета da{\displaystyle da} при постоянном катете b{\displaystyle b} приводит к приращению гипотенузы dc{\displaystyle dc}, так что

dadc=ca{\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}

Методом разделения переменных из них выводится дифференциальное уравнение c dc=ada{\displaystyle c\ dc=a\,da}, интегрирование которого даёт соотношение c2=a2+Const{\displaystyle c^{2}=a^{2}+\mathrm {Const} }. Применение начальных условий a=0,c=b{\displaystyle a=0,c=b} определяет константу как b2{\displaystyle b^{2}}, что в результате даёт утверждение теоремы.

Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Подобные геометрические фигуры на трёх сторонах[править | править код]

Обобщение для подобных треугольников, площадь зелёных фигур равны площади синей. Теорема Пифагора с использованием подобных прямоугольных треугольников.

Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах», перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур^[10]: сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями A{\displaystyle A}, B{\displaystyle B} и C{\displaystyle C}, построенных на катетах с длинами a{\displaystyle a} и b{\displaystyle b} и гипотенузе c{\displaystyle c} соответственно, имеет место соотношение:

Aa2=Bb2=Cc2⇒A+B=a2c2C+b2c2C{\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,\Rightarrow \,A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C}.

Так как по теореме Пифагора a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}, то выполнено A+B=C{\displaystyle A+B=C}.

Кроме того, если возможно доказать без привлечения теоремы Пифагора, что для площадей трёх подобных геометрических фигур на сторонах прямоугольного треугольника выполнено соотношение A+B=C{\displaystyle A+B=C}, то с использованием обратного хода доказательства обобщения Евклида можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить конгруэнтный начальному прямоугольный треугольник площадью C{\displaystyle C}, а на катетах — два подобных ему прямоугольных треугольника с площадями A{\displaystyle A} и B{\displaystyle B}, то оказывается, что треугольники на катетах образуются в результате деления начального треугольника его высотой, то есть сумма двух меньших площадей треугольников равна площади третьего, таким образом A+B=C{\displaystyle A+B=C} и, применяя соотношение для подобных фигур, выводится теорема Пифагора.

Теорема косинусов[править | править код]

Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике^[11]:

Разработка урока внеурочной деятельности «Четырехугольники и их виды»

Логика 5 класс

Тема: «Четырехугольники и их виды.»

Целеполагания:

• познакомить ребят с историей возникновения четырехугольников;

• рассмотреть виды четырехугольников и их элементы;

• способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;

• содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность

Задачи:

— Продолжить формирование навыков контроля результатов деятельности.

— Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.

— Формирование логического, абстрактного, эвристического, системного мышления.

Оборудование: проектор, экран, компьютер, презентации

План.

1. Организационные моменты.

Сообщение темы, целей и задач урока.

2. История возникновения четырехугольников.

Заглянем в прошлое, когда зародилась наука геометрия….

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.

Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т.д.

А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.

Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки и с их помощью перетаскивать грузы. Так появилось первое колесо.

Но не только в процессе работы знакомились люди с геометрическим фигурами.

Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).

Для того, чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы.

Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д.

Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов.

Пирамиды – а они построены более 5 тыс. лет назад – состоят из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.

«Все боится времени, но само время боится пирамид».

В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра.

Без математических знаний все эти сооружения невозможно было бы построить. И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.

Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: «Не знающие геометрии не допускаются!»

Настает время привести все разрозненные знания в систему.

Геометрия… откуда взялось это слово? Что оно означает? Попробуем разгадать его смысл. Ведь вам постоянно встречаются похожие слова: география, геология, геодезия… а есть еще геоботаника и т.п. это все названия различных наук или разделов наук. Со смыслом слова география вы уже знакомы. «Гео» означает «Земля», «метр» — это единица измерения длины (от греческого слова «метрео» — «измеряю». Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».

«Геометрия была открыта египтянами и возникла при измерении земли. Нет ничего удивительного в том, что эта наука как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного состояния переходит в совершенное. Зарождаясь путем чувственного восприятия, оно постепенно становится предметом рассмотрения и наконец, делается достоянием разума». Эти замечательные слова приписывают греческому ученому Евдему Родосскому, жившему в IV в.до н.э.

В «Энциклопедическом словаре юного математика» написано: «Геометрия – одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках».

И наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах «Начала». Евклид жил в Александрии, был современником царя Птоломея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии. В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида.

Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.

В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах.

3. Что изучает геометрия.

Геометрия – это раздел математики, которая изучает пространство, а также всяческие отношения, который в этом пространстве возникают. Всю геометрию можно разделить на несколько типов. Например, классическая геометрия решает все вопросы связанные с точками, прямыми, плоскостями и т.д. Она сама включает в себя планиметрию, стереометрию и другие дисциплины. Существует также аналитическая геометрия, которая построена на координатном способе познания. Например, именно таким способом изучаются вектора, прямые и отрезки, которые заданы формулами и условиями. Также существует дифференциальная геометрия, которая задается дифференциальными уравнениями, а также занимается отображением этих уравнения в различных пространствах. И завершает это ряд такая дисциплина как топология, которая изучает непрерывность в наиболее общем виде.
Считается, что родоначальниками геометрии были греки, которые впервые опубликовали свои первые труды, например, знаменитые «Начала» Евклида. Греки занимались сравнением различных фигур, а также их принадлежность друг другу. Такая геометрия занималась простейшими фигурами, на плоскости и в пространстве.
Средние века не много дали геометрии, а вот уже в XVII веке Декарт придумал свой координатный метод, что заставило геометрию сделать новый виток в своей истории. Также кооринатный метод используется и в другом виде геометрии — дифференциальном, ГД координаты занимают одну из ведущих ролей. В дифференциальной геометрии все задается уже относительно гладкими графиками, что является более сложным и более развитие уровнем геометрии.
Сегодня геометрия используется довольно широко в прикладных моментах. Она касается не только обмера земли (как и тысячелетия назад) а также и другими, более развитыми и более сложными научными вычислениями.

4. Знакомство с четырехугольниками.

Параллелограмм

Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

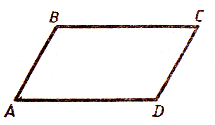
Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.

Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.

1 признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.

2 признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

3 признак параллелограмма. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Трапеция

Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.

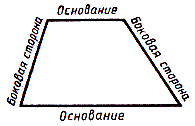
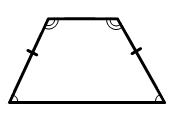
Трапеция называется равнобедренной (равнобочной), если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.

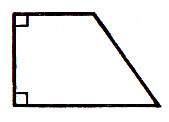
Трапеция, один из углов которой прямой, называется прямоугольной.

Прямоугольник

Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.

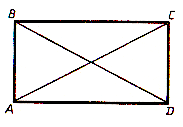
Свойство. Диагонали прямоугольника равны.

Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

Ромб

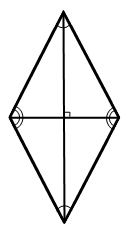
Определение. Ромбом называется параллелограмм, у которого все стороны равны.

Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадрат

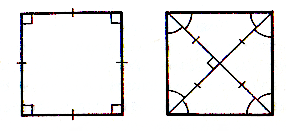
Определение. Квадратом называется прямоугольник, у которого все стороны равны.

Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.

Свойства:
1. Все углы квадрата прямые

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Математическая сказка о том, как подружились Квадрат и Прямоугольник.

В некотором царстве, в некотором государстве жил-был Прямоугольник, а по соседству с ним жил Квадрат.

Квадрат очень хотел подружиться с Прямоугольником, но он был маленьким, а Прямоугольник большим. Однажды ночью Квадрат взял ножницы, подкрался к дому Прямоугольника и отрезал у него половинку так, что Прямоугольник стал квадратом. Квадрат приставил к себе отрезанную половинку и стал прямоугольником. Наступило утро. Прямоугольник-Квадрат пришёл домой к Квадрату-Прямоугольнику и сказал: «Я бы сам отдал тебе свою половинку, если бы ты об этом попросил». Квадрату стало стыдно за свой поступок. Он попросил прощения у Прямоугольника. Прямоугольник простил его, и с тех пор они стали друзьями. Потом они часто менялись своими половинками.

Вот и сказке конец, а кто слушал – молодец!

СКАЗКА О ПРЯМОУГОЛЬНИКЕ

Жили-были в чудесной стране Геометрии Карандаш и Линейка. Как-то раз задумали они начертить четырехугольник, у которого все углы – по 90о. Чертили-чертили целый день. Особенно старалась Линейка. Она ложилась ровно, не наклоняясь. Карандаш отчетливо проводил и соединял линии. В конце концов у них получилась такая фигура . На радостях отправились они к своему другу Транспортиру. Он жил неподалеку от наших героев. Это был удивительно трудолюбивый и внимательный инструмент. Он напоминал половину круга, и поэтому его еще иногда ласково называли Пирожок. Пришли наши герои и попросили у него помощи:

– Послушай, Пирожок, помоги нам. Мы целый день чертили фигуру, у которой все углы должны быть по 90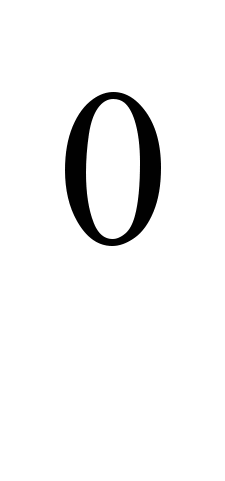. А так ли у нас получилось, мы не знаем. Проверь, пожалуйста.
А у Транспортира на спинке было много делений от 0 до 180. Проверка величины углов – его самое любимое занятие. Поэтому он, конечно, согласился. Все углы у четырехугольника действительно были равны 90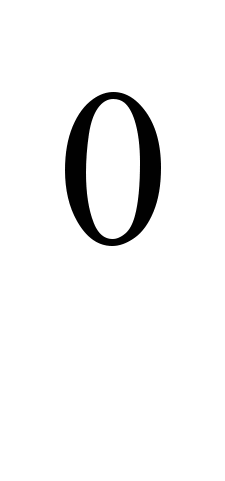. А потом он улыбнулся и сказал:
– Угол, равный 90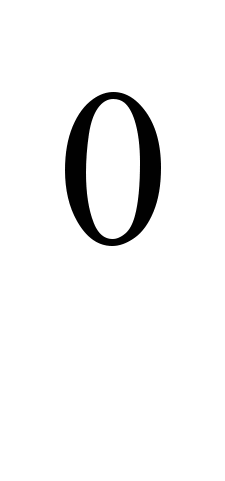, – это прямой угол, а четырехугольник, у которого все углы – по 90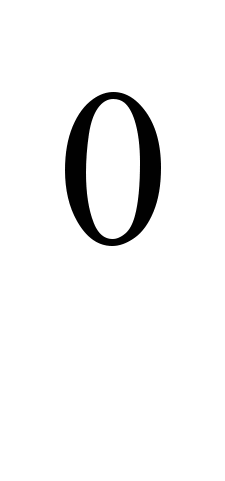, называется прямоугольником. В следующий раз, когда соберетесь что-нибудь чертить, – сказал Транспортир, – не забудьте про меня. Я обязательно приду к вам на помощь, и дело быстрее сладится.
И еще он добавил:
Раз, два, не ленись,
Дружно за дело вместе берись!
 

СКАЗКА О КВАДРАТЕ

Жил-был в стране Геометрии Лист. Его края были неровными, с множеством загибов, потому что его вырвал из тетради мальчик по имени Вовка, и уже долгое время Лист находился в пути. А нашему герою очень хотелось, чтобы все его стороны стали вновь ровными.
Собравшись с силами, Лист отправился на поиск Линейки, Карандаша и Ножниц. Только они могли ему помочь. Лист целых пять дней провел в пути, потому что двигаться он мог только с помощью ветра, а ветреная погода была не каждый день. На шестой день своего пути Лист встретил Карандаша. Карандаш в это время чертил углы на песке. Его углы были разной величины, и он упорно повторял вслух: «Острый, тупой, прямой, развернутый!». Лист тихонько подлетел к Карандашу и рассказал свою историю. Карандаш его пожалел и согласился помочь, но, к сожалению, без Линейки и Ножниц он ничего сделать не смог.
Теперь они отправились в путешествие уже вдвоем. Но Линейку им не пришлось долго искать, потому что она вместо мостика лежала на двух противоположных берегах ручья. Карандаш и Лист аккуратно перетащили Линейку на свой берег и попросили ее помощи.
– Да! Да! Да! – воскликнула Линейка (так соскучилась она по своей работе). – Конечно, помогу!
Началась работа. Карандаш чертил ровно. Линейка замеряла стороны так, чтобы все они были одинаковой длины. Когда работа была сделана, Линейка объявила Листу:
– Ну, теперь ты будешь квадратом!
– Квадратом? – удивился Лист.
– Да! Да! Квадратом! – убедительно ответила Линейка.
– А что это такое? – спросил Лист.
– Это прямоугольник, у которой все стороны не только ровные, но и равные, – сказала Линейка.
Лист обрадовался. Он поблагодарил Карандаша и Линейку и отправился на поиски Ножниц.

Идя по дорожке, Лист увидел красивый домик с очень необычной акацией вместо забора. Он поднялся по ступенькам и постучался. Дверь тихонько заскрипела, и к нему навстречу вышли Ножницы. Радость Листа невозможно было описать. Он прыгал от счастья. А Ножницы в это время смотрели на него и не понимали, в чем дело. Наконец Лист успокоился и рассказал Ножницам свою историю.
Ножницы повели себя необычно, они вдруг стали резать воздух. Это оказалось, они так выражали свое удовольствие. Ножницы действительно очень любили работать, то есть резать. Через пять минут наш Лист превратился в настоящий Квадрат. Ножницы принесли ему зеркало. Он долго смотрелся в него, а потом закричал:
– Квадрат! Квадрат!
А Ножницы опять стояли в недоумении и смотрели на Лист. Они не понимали, что это за слово повторял наш герой. Но мы-то с вами знаем, что это за фигура.

Ромб и квадрат

В тридесятом царстве Многоугольников, в тридевятом царстве Выпуклых многоугольников жил- был боярин по имени Параллелограмм. Надоело ему жить одному и решил он жениться. В невесты себе выбрал раскрасавицу соседку Равнобедренную Трапецию. Прошло немного времени и родился у них сынок Прямоугольник. Весь в родителей пошел!

От отца у него были бока попарно параллельны, а от матери достались равные диагонали. Но было у него свое личное достоинство – прямой угол, видимо, от предков достался. И от этог8о вырос он гордым, прямоугольным.

Не мог найти он друзей во всем государстве. Решил прямоугольник отправиться в путешествие. Сказал родителям: «Пока не найду себе друга – не вернусь». Что делать? Погоревали родители, но благословили его, и пошел он по земле геометрической.

Шел, шел, зашел в лес дремучий, видит избушка стоит. Зашел в избушку. А в этой избушке жили братья-сироты Квадрат, да Ромб. Познакомились, понравились друг другу. Проговорили всю ночь. Поведал им свое горе Прямоугольник. Братья и говорят: «У нас тоже есть прямой угол, не расстраивайся, мы будем с тобой дружить».

Отправились они вместе к отцу и матери Прямоугольника. Боярин и боярыня хорошо их приняли, пригласили остаться жить у себя. Братья с охотой согласились. И стали они вместе дружно поживать.

А про какой прямой угол говорили квадрат и ромб?

5. Итоги урока

Что вы сегодня узнали на уроке? Что больше всего запомнилось?

6. Домашнее задание.

Придумать математический сказку о любом из четырехугольников.