Интересные факты о математике

Приветствуем вас на сайте Interessno.ru, наши уважаемые читатели. Математика — это достаточно сложная наука. По этой причине большинство школьников и студентов ужасно не любят уроки математики. Однако, на самом деле, математика — это очень интересная наука. Чем больше ее изучаешь, тем она становится более таинственной и волшебной. И сегодня мы постараемся вам это доказать.
Мы собрали в одной публикации самые интересные факты о математике. Надеемся, из всех фактов, хоть какой-то будет для вас новым и интересным.
№1

Умножение одинаковых значений с цифрой 1 всегда дает палиндромные числа. Палиндромными называются числа перевертни, значение которых читается в разные стороны одинаково. Например, если взять 111 111 111 и умножить его на такое же 111 111 11, то получится значение 12 345 678 987 654 321. И это работает на убывание. Возьмите 111 111 и перемножьте с 111 111 и получите 12 345 654 321.
№2

Слышали когда-то о «Константе Капрекара». Сейчас мы вам покажем магию цифры 6174. Начиная с любого четырехзначного числа (у которого как минимум есть 2 разных цифры), просто выполните такие шаги:
- Расположите цифры четырехзначного числа в порядке убывания/возрастания. К примеру, из 3451, делаем 5431.
- Вычтите из большего значения меньшее.
- Повторите вышеописанный пункт.
В конечном итоге вы всегда окажетесь на цифре 6174, которая является «Постоянной Капрекара». Также, стоит отметить, что для достижения «константы» нужно совершить не более 7 манипуляций. К примеру, берем значение 4551. располагаем цифры в порядке убывания — 5541. Получается следующая картина:
Этап 1 : 5541-1455 = 4086
Этап
2 : 8640 — 0468 = 8172
Этап 3 : 8721 — 1278 =
7443
Этап 4 : 7443 — 3447 = 3996
Этап 5 :
9963 — 3699 = 6264
Этап 6 : 6642 — 2466 = 4176
Этап
7 : 7641 — 1467 = 6174
№3

Цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 представляют число 100. Есть как минимум три разных способа получить из этих цифр «сотню».
Способ 1: 123+4-5+67-89=100.
Способ 2: 123-4-5-6-7+8-9=100.
Способ 3: 1+23-4+5+6+78-9+100.
№4

Доказательство №1:
Если N=0.999, тогда 10N=9.99.
10N-N будет равно 9.99-0.999, следовательно, 9N=9. Следовательно, N=1.
Доказательство №2:
Если N=0.999, то N, деленное на 9, будет равняться 0.111.
Выразим это в качестве уравнения:
0.111=1/9.
Умножение обеих сторон на 9 дает:
0.999=1.
№5

Значение 2520 является наименьшим числом, которое можно разделить на все цифры начиная от 1 и заканчивая цифрой 10.
№6

Число 9 считается магическим, так как имеет некоторые удивительные свойства. Магическим 9 называют по той причине, что если умножить любое число на 9 и сложить все цифры, которые получились в результате умножения, то мы снова получим все ту же 9. К примеру, если мы возьмем число 8 и умножим на 9, то получим 72 (7+2=9). Если возьмем цифру 5 и умножим на 9, то получим 45 (4+5=9). Если возьмем цифру 81 и умножим на 9, получим число 729. Если сложим 7+2+9, получим 18. Если сложим 1+8, то получим все то же число 9. И так со всеми результатами.
№7

Во многих культурах число 13 считается несчастливым, по крайней мере, существует много мифов вокруг него. Например, в некоторых древних европейских религиях было 12 основных добрых богов и один злой. Он как раз таки и был 13-м божеством. Также, во время так называемой Тайной вечери, когда Иисус собрал за столом своих апостолов (их было 12, а с Иисусом было 13 человек), там же был его ученик Иуда, который предал его за вознаграждение.
№8

Удивительно, но среди всех фигур, с одинаковым периметром, круг имеет самую большую площадь. При этом, среди всех фигур, с одинаковой площадью, круг будет иметь самый короткий периметр.
№9

Символы используемые для сложения (+) и вычитания (-), были изобретены тысячи лет тому назад, однако только в 16-м веке было изобретено большинство других математических символов. До этого времени математические уравнения записывали словами, что занимало достаточно много времени. Тот же знак равно (=), был изобретен математиком Робертом Рекордом только в 1557 году.
№10

Когда-то маленькому мальчику Карлу Гауссу учитель математики задал решить очень сложную задачку. Он попросил его найти сумму всех натуральных чисел от 1 до 100. Буквально через минуту маленький мальчик дал ответ учителю.
Удалось решить эту задачу ему благодаря смекалке. Он нашел закономерность. Приведем ее на примере чисел от 1 до 10.
Достаточно сложить 1+2+3+4+5+6+7+8+9+10. Вроде ничего необычного нет. Но что же сделал юный Гаусс? Он сгруппировал их следующим образом: (1+10)+(2+9)+(3+8)+(4+7)+(5+6). В этих группах также нет ничего необычного. Но если всмотреться, сумма всех чисел всегда равна 11. Всего 5 групп. То есть, если мы умножим 11 на 5 (количество групп), получим значение 55. Это и будет ответ.
Гаусс сделал это со всеми числами и получил 50 групп и число 101 (100+1=101, 99+2=101 и т. д.). В итоге ответ получился 5050. Сегодня данный метод называется «Методом Гаусса».
№11

Если у вас получится сложить лист бумаги пополам 103 раза, то вы получите размер наблюдаемой вселенной. На практике, мировой рекорд по сгибанию листа бумаги пополам составляет всего 12 раз. Если, теоретически (такое в реальности невозможно), у вас получится складывать лист и дальше, то вы быстро начнете получать большие толщины.
№12

Еще в 1900 году, чуть более 100 лет тому назад, все мировые математические знания могли поместиться приблизительно в 80 книгах. Сегодня все математические знания даже не поместятся в 100 000 книг.
Рекомендуем также прочитать: Интересные факты о богомолах
№13
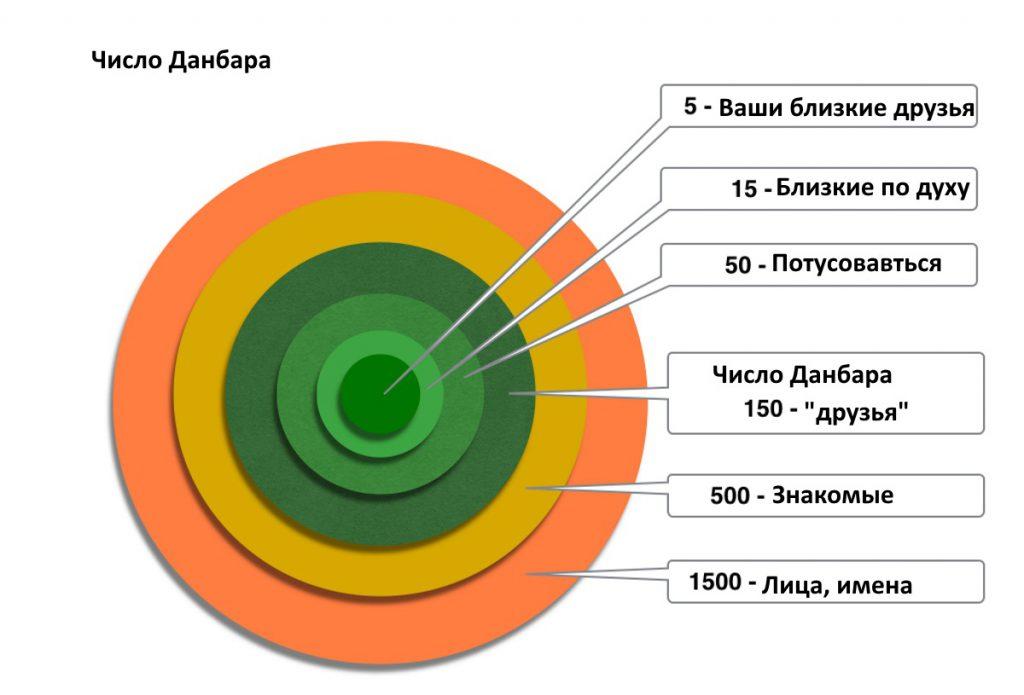
Число Данбара — это теоретически верхний предел постоянных социальных отношений, которые можно поддерживать. Оно находится в диапазоне от 100 до 230 (среднее 150). Таким образом, если население города ниже числа Данбара, то большой шанс того, что все члены города будут жить в гармонии и мире, чем жители крупного города, где проживает более 230 человек.
На этом наша статья подошла к завершению, дорогие читатели. Надеемся, эти математические факты были интересными как школьникам, так и тем, кто уже давным-давно закончил школу.
Кобылинский Александр
Профессиональный блогер и штатный автор сайта Interessno.ru. Последним достижением стало получение двух высших образований (магистратура) в разных сферах деятельности.
Последние записи автора Кобылинский Александр (посмотреть все)
топ-10 самых удивительных для детей, учеников 5 класса
«Математика» в переводе с греческого языка означает наука, знание или изучение. Это слово впервые было употреблено еще в трудах Аристотеля в 4 веке до нашей эры. История математики как науки берет свое начало с древних времен, когда пещерные люди для обозначения количества чертили палочки на каменных стенах своих пещер.
Сегодня математику принято делить на два вида: теоретическую (на ее основе выполняются различного рода анализы и расчеты) и прикладную (созданные математиками модели служат в других областях науки или инженерии).
С этой древней наукой связано много удивительных историй и за долгое время возникали различные нестандартные теории. В этой статье поговорим о 10 интересных фактах о математике для детей, учеников 5 класса.
10. Нобель отказался включать математику в список наук для премии

Альфред Нобель был выдающимся изобретателем и инженером. Накопленные им за всю жизнь деньги были завещаны им для присуждения одноименной премии ученым и первооткрывателям из различных областей наук. Но, по странному стечению обстоятельств, среди перечня награждаемых наук не оказалось математики.
По какой же причине Нобель отказался включать математику в список наук для премии
? Самой распространенной версией произошедшего считается личная обида изобретателя на всех математиков. Якобы Нобель застал свою неверную жену с любовником, который по роду своей деятельности относился к математикам. Однако эта теория разбивается при изучении биографии ученого: он никогда не был женат, а все женщины в его жизни не имели отношения к математике и математикам!Второй версией стала личная неприязнь к ученому-математику Миттагу-Леффлеру, который обращался к Нобелю за финансовой помощью и делал это слишком навязчиво. Также этот ученый учредил свою именную премию за открытия в области математики и Нобель не захотел конкурировать с ним в этом все по тем же личным причинам.
Но это все домыслы, не имеющие реального подтверждения. Скорее всего, математика не была включена в список номинируемых наук по личному несерьезному отношению к ней со стороны Альфреда. Он занимался работой в области химии, физики и литературы, признавал достижения медицины, а в математике, по его личному мнению, открытий никаких не предвиделось, да и пользы в развитии человечества она не приносила.
9. 666 – сумма всех чисел на рулетке

В христианстве 666 считается Числом Зверя, и многие неудачи в жизни связывают с этими знаковыми цифрами.
Примечательным является тот факт, что 666 – это сумма всех чисел на рулетке. Такой результат получается при сложении последовательных чисел, расположенных в 37 секторах, начиная с нуля. Благодаря магическому значению суммы чисел рулетка и получила свое второе название – чертово колесо.
8. Египтяне придумали Десятичную систему

Во второй половине III тысячелетия до нашей эры египтяне придумали Десятичную систему. Она носит название непозиционной, а цифры, придуманные древними египтянами, относятся к иероглифическому письму. В те временя в Египте писали на папирусе, поэтому до наших времен сохранилось незначительное количество артефактов.
Но благодаря им и стало известно, что Десятичная система счисления зародилась именно в Египте, а уже позже математики Греции и Вавилона учились у египтян.
7. Знак «равно» придумал в XVI веке Роберт Рекорд

В математике используется большое количество специальных символов. Один из таких знаков, а именно знак «равно» придумал в 16 веке Роберт Рекорд. В своем труде он ввел два параллельных штриха и обосновал их словами: «никакие другие вещи не могут быть более равными».
Однако этот математический знак вошел в обиход далеко не сразу. Только в конце 17 – начале 18 века знак «=» был введен в Европе Лейбницем. К тому времени прошло более 100 лет с момента смерти математика Рекорда, использовавшего его первым.
6. Льюис Кэрролл более 25 лет преподавал математику

Льюис Кэрролл был человеком разносторонним и занимался фотографией, логикой, философией, писал произведения художественной литературы. Его известные книги «Алиса в стране чудес» и «Алиса в Зазеркалье» известны во многих странах.
Помимо всех вышеперечисленных увлечений, он был профессором Оксфордского университета, Льюис Кэрролл более 25 лет преподавал математику. Будучи студентом Льюис учился не очень хорошо, но за свои выдающиеся способности в математике получил степень бакалавра и выиграл конкурс на чтение лекций по математике в колледже Крайст-Чёрч. Это занятие было ему скучно, но приносило хорошие деньги, поэтому читал он их на протяжении 25 лет.
5. Существует американская и английская системы определения больших цифр

Существуют американская и английская системы определения больших цифр. Обе этих системы были изобретены во Франции физиком и математиком Николасом Шоке.
Для американской системы характерно построение названия больших цифр в следующем прядке: в начале латинское порядковое числительное, в конце к названию добавляется суффикс «-иллион». Например, квадриллион, квинтиллион, секстиллион. Исключение составляет число миллион: оно образовано корнем милл и увеличительным суффиксом «–ион». Эта система наименования чисел используется в США, Канаде, России и Франции.
Английская (европейская) система распространена во всем мире. Названия чисел строятся следующим образом: к латинскому числительному добавляется суффикс «-иллион», а название следующего числа, которое в 1000 раз больше, образуется от того же числительного с добавлением суффикса «-иллиард». То есть после триллиона идет триллиард, а затем квадриллион, квадриллиард и т.д.
4. В системе римских цифр отсутствует 0

Римские цифры относятся к непозиционной системе счисления. Появилась она в давние времена за 500 лет до н. э. Натуральные числа здесь записываются посредством повторения цифр по определенному правилу: если большая цифра стоит перед меньшей, то обе цифры складываются, если же большая цифра стоит за меньшей, то меньшая вычитается из большей.
В системе римских цифр отсутствует 0. Ноль был введен вавилонскими математиками 300 лет до н. э. и выполнял роль пробела. То есть он был не цифрой, а знаком, используемым в составе чисел кратных десяти. Для непозиционной римской системы такая цифра, как 0, не актуальна. 0 – это отсутствие числа, а римляне не записывали то, чего нет.
3. Абрахам де Муавр смог вычислить день своей смерти

Этот математик жил в 18 веке. Он занимался работой в области теории вероятности и вывел формулу Муавра. Абрахам де Муавр смог вычислить день своей смерти, и сделал это безошибочно.
Он умер в 87 лет. По своим наблюдениям, пожилой человек заметил, что стал вялым и все больше спал. Математик вычислил, что в среднем каждые сутки его отдых увеличивается на 15 минут, а значит придет тот день, когда сон увеличится до 24 часов, это и будет день его смерти. На основании таких расчетов он назвал дату, в которую и скончался, 27 ноября 1754 года.
2. Числа, наделенные необыкновенными свойствами

Существуют числа, наделенные необыкновенными свойствами. Число 7 занимает особенное место в общей мировой культуре. В радуге семь цветов, в неделе семь дней, в мире семь чудес света, а в религиозном веровании семь смертных грехов. Сумма точек на противоположных сторонах игральной кости всегда равна 7.
Число 9 обладает особыми магическими свойствами. Если умножить любое число на 9, а затем сложить все цифры между собой, пока не получится однозначное, то результат всегда будет 9.
1. У каждого народа есть свои «несчастливые» числа

У каждого народа есть свои «несчастливые» числа. Так, например, в Китае, цифра 4 произносится созвучно со словом «смерть», поэтому китайцы не любят это число. В Тайбее же не разрешено употреблять цифру 4, и даже во многих сооружениях отсутствует 4 этаж, есть третий, а потом сразу пятый.
Итальянцы относятся с нелюбовью к числу 17, еще со времен Древнего Рима. Тогда на надгробиях писалась фраза: «Меня больше нет», визуально она выглядела как VIXI, что в римской системе счисления обозначает цифры 6 и 11, а сумма их равна 17.
Число 666 во многих странах мира заменили или убрали на многих объектах. Так оно исключено из нумерации дорог, телефонных кодов.
Интересные факты о математике — Альтернативный взгляд Salik.biz
Человек может и не быть математиком. Более того, он может даже не знать эту науку на минимальном уровне, но тяжело отрицать – математику человек видит практически везде. Цифры, фигуры и математические законы преследуют человека повсюду, поэтому нелишним будет узнать кое-что об этой науке.

1. Абрахам де Муавр (математик из Англии) в своей глубокой старости вдруг понял, что его сон увеличивается на 15 минут в каждый последующий день. После этого он составил прогрессию и определил тот день, когда сон займет весь день. Случилось это 27 ноября в 1754 году, и это был день его смерти.

2. Религиозные и верующие евреи стараются всеми силами избегать любых знаков, которые связаны с крестом или символику Христа. К примеру, вместо плюса в школах используют перевернутую «Т».
3. Подлинность денежной купюры евро всегда можно узнать по ее серийному номеру – это буква и 11 цифр. Необходимо поменять букву на то число, которое является порядковым номером этой буквы в алфавите. После этого необходимо сложить все числа и складывать результаты до тех пор, пока не будет одна цифра. И если в итоге получится 8, это говорит о подлинности купюры. Другой способ – сложение всех цифр, без буквы. Итоговый результат, состоящий их буквы и цифры, должен подходить под ту страну, на территории которой появилась купюра. К примеру, Германия – это Х2.

4. Есть версия, что Альфред Нобель отказался включать математику в длинный список наук для своей премии по личным причинам – жена Альфреда спала с математиком. Но в действительности Нобель был холостым. Нет достоверных доказательств того, почему математику не включили, однако есть предположения. К примеру, уже тогда существовала своя премия, но созданная шведским королем. Другая версия – математика является чисто теоретическим предметом, поэтому математики не способны сделать ничего действительно важного для людей и человечества в целом.
Рекламное видео:
5. Есть такая фигура, как треугольник Рело. Она образовывается через пересечение трех идентичных по радиусу кругов, причем центры этих кругов расположены в вершинах треугольника с равными сторонами. Сверло, созданное на основе этого треугольника, дает возможность сверлить только квадратные отверстия. При этом стоит помнить, что сверление таких отверстий с использованием треугольника Рело может иметь погрешность в 2 процента.

6. В русской литература и математике 0 не относится к спискам натуральных чисел, однако на западе 0 является одним из представителей множества таких чисел.

7. Джордж Данциг, математик из Америки, будучи всего лишь университетским аспирантом, один раз опоздал на занятие и, увидев несколько уравнений и подумал о том, что эти уравнения являются общими домашними задачами, которые необходимо выполнить. Это задание показалось ему намного сложнее того, что давали обычно, но он их выполнил и принес результаты преподавателю. И только после этого он узнал, что смог решить 2 нерешаемых уравнения статистики. Причем это были те задачи, которые не могли решить ученые в течение нескольких лет.

8. Если сложить все числа в рулетке, получится 666.

9. Небезызвестная Софья Ковалевская познакомилась с этой наукой о числах в далеком детстве – в ее комнате не было обоев, были лишь лекции ученого Остроградского об исчислениях.

10. В Индиане (штат США) в 1897-ом году выпустили билль, согласно которому число Пи будет равно 3,2. Однако билль не превратился в закон благодаря тому, что в этот процесс вовремя вмешался университетский профессор.
Интересные факты о числах
В Китае, Корее и Японии число 4 считается несчастливым, так как созвучно слову «смерть». В этих странах этажи с номерами, оканчивающимися на четыре, почти всегда отсутствуют.
Арабы пользуются собственными знаками для записи цифр, хотя арабы Европы и Северной Африки применяют привычные нам «арабские» цифры. Однако какими бы не были знаки цифр, арабы пишут их, как и буквы, справа налево, но начиная с младших разрядов. Получается, что если мы встретим знакомые цифры в арабском тексте и прочитаем число привычным образом слева направо, то не ошибёмся.
У сороконожки вовсе не обязательно 40 ножек. Сороконожка — это бытовое название разных видов членистоногих, объединённых по-научному в надкласс многоножек. У разных видов многоножек от 30 до 400 и выше ног, причём это число может быть разным даже у особей одного вида. В английском же языке устоялись два названия для этих животных — centipede («стоножка» в переводе с латыни) и millipede («тысяченожка»). Причём разница между ними существенна — тысяченожки не опасны для человека, а стоножки очень больно кусаются.
На эмблемах Олимпийских игр год обычно обозначается двумя (например, Барселона-92) или четырьмя цифрами (например, Пекин-2008). Но один раз год был обозначен пятью цифрами. Это случилось в 1960 году, когда Олимпиада проходила в Риме — число 1960 было записано как MCMLX.
В 522 микрорайоне Харькова по плану должны были построить блок жилых домов, чтобы с воздуха они образовывали буквы СССР. Однако после постройки трёх букв С и вертикальной черты буквы Р в план внесли изменения. В результате сейчас эти дома можно увидеть как число 666.
В большинстве европейских языков названия числительных от 20 до 90 образуются по стандартной схеме — созвучно с базовыми числами от 2 до 9. Однако во французском языке названия некоторых чисел имеют странную логику. Так, число 70 произносится ‘soixante-dix’, что переводится как «шестьдесят и десять», 80 — ‘quatre-vingts’ («четырежды двадцать»), а 90 — ‘quatre-vingt-dix’ («четырежды двадцать и десять»). Похожая ситуация в грузинском и датском языках. В последнем число 70 буквально переводится как «полпути от трижды двадцать до четырежды двадцать».
В русском языке названия числительных до 100, делящихся на 10, образуются сложением названия цифры и «десять»: двадцать, тридцать, пятьдесят и т. д. Исключением из этого ряда является число «сорок». Объясняется это тем, что в древности условной единицей торговли меховыми шкурками была связка из 40 их штук. Ткань, в которую заворачивались эти шкурки, и называлась «сорок» (от этого же корня происходит слово «сорочка»). Таким образом название «сорок» вытеснило более древнее «четыре десте».
Английский антрополог Роберт Данбар выявил взаимосвязь между размером новой коры больших полушарий головного мозга приматов и размером их стаи. На основании этих данных он определил оптимальный размер социальных связей для человека — 150. Такое число находит подтверждение в самых разных исторических периодах и локациях: например, это оценочное число жителей неолитического поселения или размер базового подразделения римской армии. В 2010 году Данбар начал исследование социальной сети Facebook и пришёл к выводу, что его число действует и там: несмотря на то, что некоторые люди имеют в социальных сетях сотни и тысячи друзей, эффективно взаимодействовать средний человек способен не более чем со 150 контактами.
Цифры на калькуляторе возрастают снизу вверх, а на клавиатуре телефона — сверху вниз. Это объясняется тем, что калькуляторы произошли от механических счётных машин, где цифры исторически принято располагать снизу вверх. Телефоны же долгое время были снабжены диском, и когда стал возможен выпуск кнопочных аппаратов с тональным набором, расположение цифр на кнопках решили сделать по аналогии с диском — по возрастанию сверху вниз с нулём на конце. |

