Топ-10 интересных фактов о геометрии.

Факт 1. Знаменитый учёный и изобретатель Архимед считал геометрию важнейшей наукой на свете. Он полагал, что она может объяснить все правила, по которым функционирует мир, и именно благодаря своим геометрическим познаниям он изобрёл множество опередивших своё время механизмов. При этом сам он считал своим главным достижением открытую формулу по вычислению вписанных в цилиндр конуса (одна третья от объёма цилиндра) и шара (две трети).

Факт 2. Существуют разные виды геометрии, и не во всех из них сумма углов треугольника равна 180 градусам. Так, в геометрии Лобачевского она всегда меньше этого числа, а в геометрии Римана — всегда больше.

Факт 3. Одним из самых знаменитых учёных, когда-либо изучавших геометрию, был Евклид. Именно в его честь классическая область этой науки и называется “евклидовой”. Он сам доказал 465 теорем! И этот рекорд никогда и никем не был побит.

Факт 4. Наполеон Бонапарт, император Франции, обладал очень острым и живым умом, и он великолепно разбирался в геометрии. Эту науку он считал важной не только в военном деле, но и в целом, и император даже написал несколько серьёзных научных трудов. В его честь одна из геометрических задач позднее была названа задачей Наполеона.

Факт 5. Основы геометрии были известны египтянам ещё в начале III тысячелетия до нашей эры, и в Династическом периоде, когда вовсю велось строительство пирамид, они активно применяли эти знания. Учёные установили, что древнеегипетским инженерам было известно, что верёвка с 12 завязанными на ней узелками, разделёнными равным расстоянием, растянутая на трёх равноудалённых колышках, образует прямой угол. Также они применяли эти знания, размечая участки поймы Нила для посева сельскохозяйственных культур.

Факт 6. Знаменитый философ и учёный Пифагор доказал теорему, названную в его честь, добавив квадраты к прямоугольному треугольнику. Это было потрясающее открытие, и не все могли до конца его понять. Пифагорову теорему даже называли “ослиным мостом”, так как сам учёный пренебрежительно называл ослами тех своих учеников, кто зазубривал теорему, но не понимал её смысла.

Факт 7. Как известно, в классической евклидовой геометрии через любую точку, не лежащую на имеющейся прямой, можно провести только одну прямую линию. Но в геометрии Лобачевского можно провести не менее двух.

Факт 8. Геометрия помогала людям познавать мир с древних времён. К примеру, окружность Земли была довольно точно вычислена древнегреческим учёным Эратосфеном за столетия до того, как люди вообще признали, что Земля имеет шарообразную форму. Для этого Эратосфен воспользовался геометрическими правилами, и, как показали современные измерения, он практически не ошибся — разница между прежними и новейшими измерениями оказалась ничтожно мала.

Факт 9. Современная наука рассматривает геометрию в качестве одного из разделов математики. Но в Древней Греции между словами “математика” и “геометрия” фактически ставился знак равенства, и даже над входом в школу знаменитого Платона была написано грозное “Да не войдёт сюда тот, кто не знает геометрии”.

Факт 10. Если взять три одинаковых круга и разместить их центры в вершинах равностороннего треугольника, линии пересечения этих кругов образуют геометрическую фигуру под названием “треугольник Рело”. Свёрла, сделанные по этому принципу, сверлят квадратные отверстия с погрешностью, не превышающей двух процентов.

Понравилась статья? Поделись с друзьями!

Геометрические фигуры ◼️ виды с названиями, определение и обозначение, основные свойства, интересные факты о простых и сложных фигурах

Общая характеристика

Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.

Основные понятия о составляющих

Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.

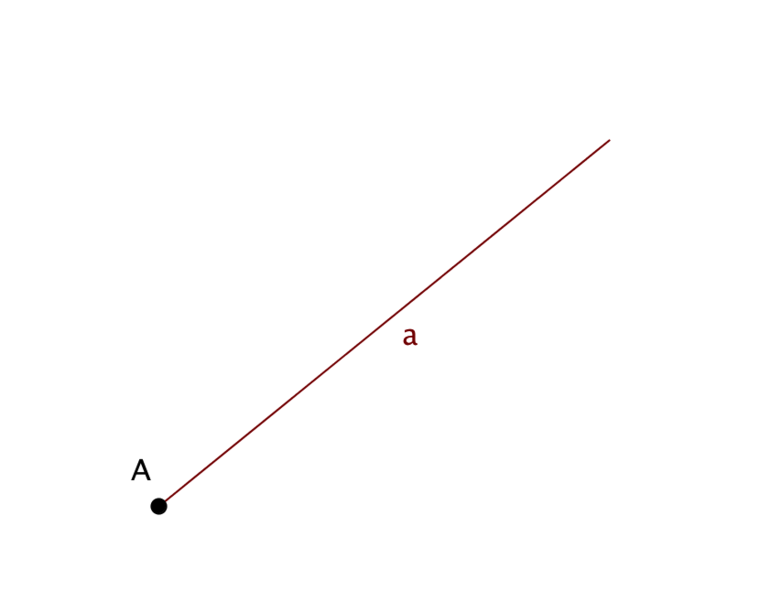
Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).

Виды линий:

• Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая. Начало и окончание не соединяются.
• Прямая. Обозначается буквой а или b.
• Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
• Кривая.Отличная от прямой линии.

Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.

Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.

Стандартные объекты

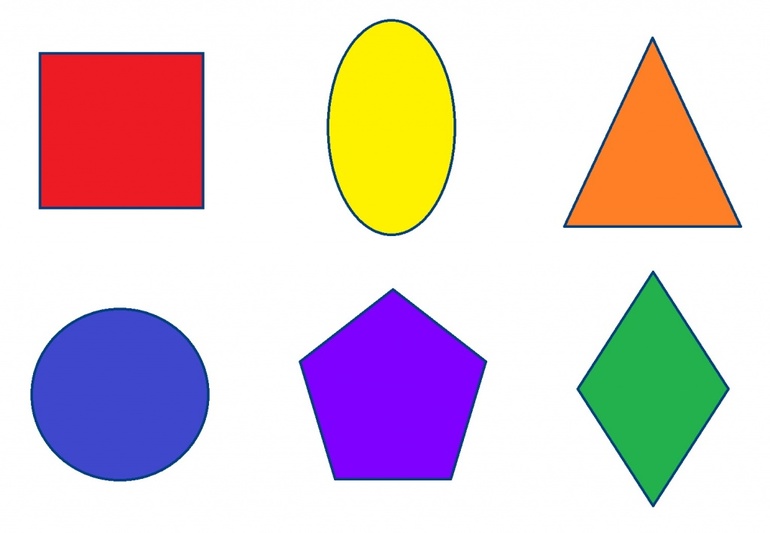
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.

Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.

Виды треугольника в зависимости от угла (У):

• Прямой. Один У будет прямым, два — менее 90 градусов.
• Острый. Градусная мера больше 0, но меньше 90 гр.
• Тупой. Один У тупой, два других будут острыми.

Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.

Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.

Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.

Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.

Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.

Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.

Сложные модели

В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.

Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.

Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).

Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.

В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.

Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.

Объемные фигуры:

• Шар.
• Конус.
• Параллелепипед.
• Цилиндр.
• Сфера.

Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.

Виды многогранников:

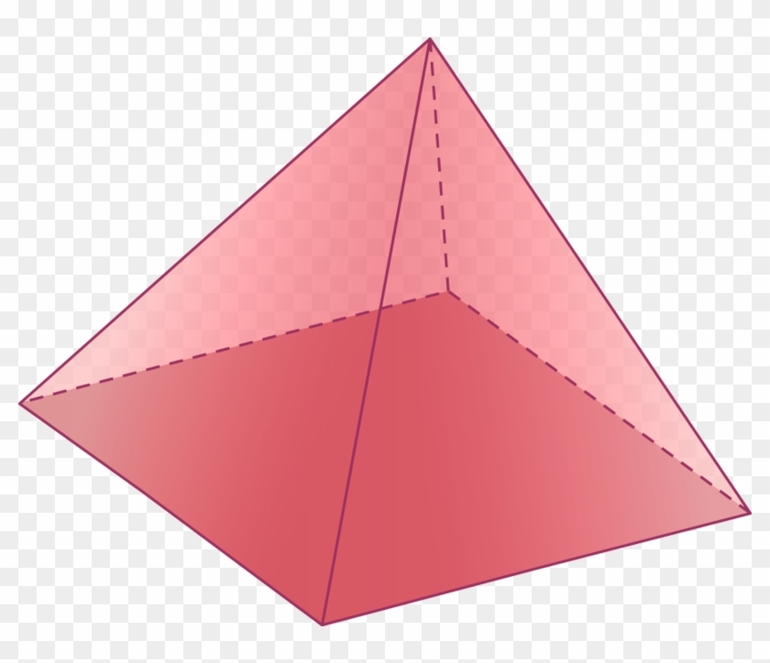
• Тетраэдер (четырехгранник). Это правильный треугольник.
• Куб (гексаэдр). Грани являются квадратом.
• Октаэдр. Имеется шесть вершин и восемь граней.
• Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
• Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.

В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.

Познавательные игрушки детям

Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.

Основной материал для обучения детей:

• Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
• Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
• Специальная детская литература.

Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.

Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.

Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.

Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.

Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.

подскажите интерестные факты о геометрии

Геометрия — важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.

Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик), от которого произошли также слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус», а термин «линия» возник от латинского «линум» (льняная нить). И факты геометрии сначала имели опытное происхождение.

Еще 5 тыс. лет назад древние египтяне знали, что если сделать на веревке 12 узелков на равных расстояниях и натянуть ее в форме треугольника, то получится прямой угол. И это было очень важно для правильной разметки плодородных земель в долине Нила. В египетских папирусах и вавилонских клинописных таблицах того времени мы находим другие геометрические факты, найденные опытным путем при измерении земельных участков, постройке зданий и т. д.

А в 5-м в. до н. э. произошел решительный поворот в развитии геометрии. И связан он с именем Фалеса, уроженца города Милет. Этот купец в свободное время занимался математикой. И сделал величайшее открытие: обнаружил, что многие геометрические закономерности можно получать не опытным путем, а с помощью рассуждения (доказательства). Это формулируют так: накрест лежащие углы, получающиеся при пересечении двух параллельных прямых третьей прямой, равны. Фалес доказал и ряд других теорем. Благодаря его открытию геометрия к 3му в. до н. э. становится наукой, в которой имеется небольшое число аксиом (первоначальных предположений), а все остальные факты (теоремы) устанавливаются с помощью доказательств. За Фалесом большой вклад в развитие геометрии внесли Евдокс, Евклид, Архимед.

И, вообще, говоря словами великого итальянского ученого Г. Галилея, «геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Что такое евклидова геометрия? | Вечные вопросы | Вопрос-Ответ

7 февраля 1832 года Николай Лобачевский представил на суд коллег свой первый труд по неевклидовой геометрии. Евклидова геометрия — это геометрия, основанная на аксиомах, сформулированных в книге Евклида «Начала»*. Выводы древнегреческого математика считались абсолютной истиной в применении к физическому миру на протяжении почти 2000 лет. Только в XIX веке было показано, что аксиомы Евклида не являются универсальными и верны не во всяких обстоятельствах — труд Лобачевского положил начало перевороту в математике.

В евклидову геометрию входят планиметрия — раздел геометрии, исследующий фигуры на плоскости, и стереометрия — раздел геометрии, в котором изучаются фигуры в пространстве.

Какие аксиомы и постулаты предложил Евклид?

В «Началах» Евклида содержались следующие утверждения, принимаемые без доказательства:

Постулаты

Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.

И чтобы каждую прямую можно было неопределённо продолжить.

И чтобы из любого центра можно было описать окружность любым радиусом.

И чтобы все прямые углы были равны между собой.

И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.

Статуя Евклида в Оксфордском университетском музее естественной истории. Фото: Commons.wikimedia.org

Аксиомы

Равные одному и тому же равны между собой.

И если к равным прибавим равные, то получим равные.

И если от равных отнимем равные, то получим равные.

И если к неравным прибавим равные, то получим неравные.

И если удвоим равные, то получим равные.

И половины равных равны между собой.

И совмещающие равны.

И целое больше части.

И две прямые не могут заключить пространства.

Что такое «неевклидова геометрия»?

Неевклидова геометрия — это геометрия, которая использует набор аксиом, отличных от аксиом евклидовой геометрии, в частности, не включает постулата о параллельных прямых. Основные открытия геометрических систем, в которых аксиомы Евклида не верны, были сделаны Николаем Лобачевским и Георгом Риманом.

Геометрия Лобачевского строится на основе тех же аксиом, что и евклидова, за исключением только одной аксиомы о параллельных. Согласно аксиоме о параллельных евклидовой геометрии, через точку, не лежащую на данной прямой а, проходит только одна прямая, которая лежит в одной плоскости с прямой а и не пересекает эту прямую. В геометрии Лобачевского принимается, что таких прямых несколько (затем доказывается, что их бесконечно много).

В геометрии Римана принимается аксиома, что каждая прямая, лежащая в одной плоскости с данной прямой, пересекает эту прямую. Эта аксиома противоречит системе аксиом евклидовой геометрии с исключением аксиомы о параллельных.

Таким образом, отличия евклидовой геометрии от геометрии Лобачевского в том, что порядок точек на прямой является линейным, т. е. подобным порядку в множестве действительных чисел, а отличие евклидовой геометрии от геометрии Римана в том, что порядок точек на прямой является циклическим, т. е. подобным порядку в множестве точек на окружности. Кроме того, в геометриях Евклида и Лобачевского каждая прямая, лежащая в данной плоскости, разделяет эту плоскость на две части; в геометрии Римана прямая не разделяет плоскость на две части, т. е. любые две точки плоскости, не лежащие на данной прямой, можно соединить в этой плоскости непрерывной дугой, не пересекая данную прямую.

---

*«Начала» (греч. Στοιχεῖα, лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. и посвященный систематическому построению геометрии.

Интересные факты об Эвклиде

Эвклид — математик, живший еще в Древней Греции. Он сумел по-новому взглянуть на пространство и положил начало современной математике. К сожалению, до наших дней дошло очень мало информации об этом математике. Представляем интересные факты об Эвклиде.

Биография

1. Где родился и жил ученый?

К сожалению, нет подлинной информации о том, где и когда родился математик. Некоторые ученые предполагают, что он появился на свет в 325 году до нашей эры. Известно лишь то, что 2,3 тысячи лет назад он жил в Александрии, где и занимался научной деятельностью.

2. Обучение.

В детском возрасте Эвклид обучался у популярного и почитаемого тогда философа Платона, который также учил Аристотеля. Стоит сказать, что сам Платон в свое время обучался у Сократа.

3. Значение имени.

В переводе с греческого его имя означает «период расцвета» или «добрая слава».

4. Исследователи математики.

Один из математиков в своем дневнике писал о том, что древнегреческий ученый мог изменить свое отношение к человеку, узнав, что он увлекается математикой. По его словам, Эвклид уважал всех математиков и относился к ним с любезностью и дружелюбием.

5. Отец.

Информация точно не подтверждена, но скорее всего, его отца звали Наукрат.

6. Смерть.

Точная дата смерти ученого также неизвестна. Но можно с уверенностью сказать, что ученый умер до 265 года до нашей эры.

Научные достижения

1. Первое научное сочинение.

Самое первое собрание научных сочинений, посвященное теме математики, было создано именно Эвклидом более чем 2 тысячи лет назад.

2. Развитие геометрии.

Эвклид поспособствовал развитию современной геометрии. Он посвятил 4 книги коническим сечениям.

3. «Начала».

Один из самых важных научных трудов великого математика — «Начала», содержавшая в себе все знания о планиметрии, стереометрии и теории чисел. Сборник книг не утратил свою популярность и в наше время. Интересно, что существуют и другие труды с таким же названием, но евклидовые «Начала» являются самыми известными и популярными. «Начала» включат в себя 13 отдельных книг, написанных самим Эвклидом, а также еще 2 книги, авторами которых являются Исидор и Гипсикл.

В России «Начала» были переведены лишь в 18 веке, а в Армении — уже в 11.

4. Эвклидова геометрия.

Геометрия, изучаемая в рамках школьной программы, и в наше время носит имя Эвклида.

5. Древние труды.

Эвклиду приписано очень много трудов, авторство которых не установлено. Эти труды относятся к самым разным областям, например, к музыке и медицине. Доказательств того, что эти работы принадлежат древнегреческому ученому нет, но многие историки, что автором является именно он.

6. Три геометрии.

В мире есть 3 геометрии: Эвклида, Лобачевского и Ремана. Самой популярной и распространенной является первая

7. Оптика и астрономия.

Научно доказано, что ученый прекрасно разбирался не только в математике, но и в оптике и астрономии. Об этом утверждают его научные труды, связанные с этими областями.

8. Теории и аксиомы.

Все теории и аксиомы сохранились в первоначальном виде. Аксиомы древнегреческого математика активно используются и изучаются и в наше время. Например, аксиома о параллельности прямых принадлежит именно ему.

9. Образец научного труда.

Труды Эвклида считаются образцом и по сей день. Связано это с тем, что в его собраниях научных сочинений все систематизировано и логически связано друг с другом.

10. Другие работы математика.

Кроме знаменитых «Начал» древнегреческому ученому принадлежат такие научные труды, как «Данные», «Явления», «О делении фигур».

11. Отец геометрии.

Эвклид по праву считается отцом геометрии, ведь именно он сумел систематизировать все полученные на тот момент математические знания. Он упорядочил все законы, принципы, теории и аксиомы, тем самым упростил изучение науки.

Истории из жизни

1. «Зачем вообще нужна геометрия?»

Эвклид занимался обучением детей, у него была математическая школа. Однажды его ученик поинтересовался, кому и зачем вообще нужна геометрия, что она может дать в дальнейшем. Выслушав вопрос, Эвклид дал мальчишке 3 золотых монеты и прогнал с урока (вероятно, такую сумму заплатили родители ученика за обучение). Он решил сразу дать прибыль ученику, если от геометрии ему нужна была лишь личная выгода.

2. «В геометрии нет царских путей».

Данная фраза относится к одной интересной легенде из жизни математика. Однажды царь захотел освоить начала геометрии и за основу взял труды Эвклида. Освоить науку царю не удавалось, а на свой вопрос о том, есть ли более простые пути изучения геометрии, получил такой ответ: «В геометрии нет царских путей».

Занимательная информация

1. Версия, что Эвклид — это группа людей.

Некоторые ученые придерживаются версии о том, что Эвклид — это не отдельная личность, а целая группа людей. На самом деле, эта версия действительно имеет место быть, так как о биографии Эвклида мы практически ничего не знаем. Эвклид точно жил, но, возможно, ему приписывают не только его достижения, но и достижения ученых, с которыми он общался и их имена не дошли до наших дней. Впрочем, это только версия, вполне возможно, что ученый был автором всех изобретений, которые, по традиции, принадлежат ему.

2. Основа работ других ученых.

Многие последователи Эвклида брали за основу своих трудов теории древнегреческого математика. В их число входит и Архимед.

3. Музыка в Древней Греции.

Современная Эвклиду музыка была тесно связана с математикой. Это объясняется тем, что мелодия писалась согласно четкому расчету звучания каждой ноты и определенным математическим правилам.

подскажите интерестные факты о геометрии

Геометрия — важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур. Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик), от которого произошли также слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус», а термин «линия» возник от латинского «линум» (льняная нить). И факты геометрии сначала имели опытное происхождение. Еще 5 тыс. лет назад древние египтяне знали, что если сделать на веревке 12 узелков на равных расстояниях и натянуть ее в форме треугольника, то получится прямой угол. И это было очень важно для правильной разметки плодородных земель в долине Нила. В египетских папирусах и вавилонских клинописных таблицах того времени мы находим другие геометрические факты, найденные опытным путем при измерении земельных участков, постройке зданий и т. д. А в 5-м в. до н. э. произошел решительный поворот в развитии геометрии. И связан он с именем Фалеса, уроженца города Милет. Этот купец в свободное время занимался математикой. И сделал величайшее открытие: обнаружил, что многие геометрические закономерности можно получать не опытным путем, а с помощью рассуждения (доказательства). Это формулируют так: накрест лежащие углы, получающиеся при пересечении двух параллельных прямых третьей прямой, равны. Фалес доказал и ряд других теорем. Благодаря его открытию геометрия к 3му в. до н. э. становится наукой, в которой имеется небольшое число аксиом (первоначальных предположений), а все остальные факты (теоремы) устанавливаются с помощью доказательств. За Фалесом большой вклад в развитие геометрии внесли Евдокс, Евклид, Архимед. И, вообще, говоря словами великого итальянского ученого Г. Галилея, «геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Занимательные факты по геометрии (9 класс) по теме: Геометрические преобразования: история возникновения и развития в математике.

Геометрические преобразования: история возникновения и развития в математике.

        Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений  и животных, гор и извилин рек, круга и серпа Луны и т д. Однако человек не только пассивно наблюдал природу, но и практически осваивал и использовал ее богатства. В процессе практической деятельности он накапливал геометрические сведения. Материальные потребности побуждали людей изготовлять орудия труда, обтесывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук, находить площади земельных участков и вместимости сосудов, вычислять объемы различных сооружений и т.д.

        Слово «геометрия» греческого происхождения(«ге»-земля, «метрео»- мерю) и означает землемерие.  О зарождении геометрии в Древнем Египте около 2000 лет до н. э. крупнейший древнегреческий историк Геродот (V в. до н. э.) пишет следующее: «Сезоострис, египетский фараон, разделив землю, дав каждому египтянину участок по жребию и взимал соответствующим образом налог с каждого участка. Случалось,  что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию».

        Развитие земледелия, строительства, ремесел и торговли требовали умения измерять и вычислять площади, объемы различных фигур и тел, а также знания свойств тех или иных фигур. Решение таких задач содержится в вавилонских клинописных табличках, в египетских папирусах, в древнекитайских трактатах “Чжоу-би” и «Математика в девяти книгах», в индийских религиозно-философских книгах, «ведах» и «сутрах»(«веда»-знание на языке санскрита), «Сульва-Сутра»-«Правила веревки».  Эти книги относятся к VII-V вв. до н. э.),а также других памятниках древности.

        В древней Греции, начиная с VII в. до н. э., происходит постепенный переход кот практической к теоретической геометрии. Разрозненные геометрические сведения,  позаимствованные у египтян и у вавилонян, ученые древней Греции дополняли, уточняли, обобщали и развивали.

        Отрывочные, эмпирические факты постепенно претворялись в систему, в цепь связанных между собой понятий, правил и положений, каждое из которых логически вытекало из предыдущего. Таким образом была создана наука, изучающая формы, размеры и взаимное расположение фигур. Эта наука по-прежнему продолжала называться геометрией, несмотря на то, что ее содержание расширилось далеко за пределы учения об измерении земли.

        Первое дошедшее до нас, полное научное изложение геометрии содержится в труде, названном «Начала» и составленным древнегреческим ученым Евклидом, жившим в III в. до н. э. в городе Александрии (ныне Египет). Эта книга вытеснила все существовавшие ранее руководства по геометрии. В течении двух тысячелетий люди изучали геометрию по «Началам» Евклида. В древней Греции, Египте, Индии, Италии, Средней Азии и других странах эта книга сотни и тысячи раз переписывалась от руки, а после изобретения книгопечатания печаталась и сотни раз переиздавалась на языках всех народов, став одной из самых распространенных книг в мире.

Наши школьные учебники тоже содержат в основном геометрический материал и научную систему, изложенную в труде Евклида. Поэтому геометрию, изучаемую в школе, иногда называют евклидовой. Новый этап в развитии геометрии  и новая научная система были открыты в XIX веке гениальным русским математиком Николаем Ивановичем Лобачевским,  создателем неевклидовой геометрии.

        Искусство изображать предметы на плоскости с древних времен привлекало к себе внимание человека. Попытки таких изображений появились значительно раньше, чем возникла письменность. Еще в глубокой древности люди рисовали на скалах, стенах, сосудах и прочих предметах быта различные орнаменты, растения, животных. При этом человек стремился к тому, чтобы отражало естественную форму предмета. Основное требование к изображению сводилось к соответствию точек натурального объекта с точками его изображения на плоскости или какой-либо другой поверхности. Длительная практика подсказала людям, каким правилам надо следовать, чтобы правильно выразить на плоскости желаемый предмет. Так возникли зачатки учения о соответствии и преобразовании.

        Слово «симметрия»-греческого происхождения («сим»-с, «метрон»-мера) и буквально означает «соразмерность». В архитектуре и искусстве оно применяется также в смысле гармоничности, равновесия, красоты.

Издавна человека, познававшего в ходе трудовой деятельности явления природы, поражала форма некоторых предметов и существ: очертания листьев на деревьях, расположение лепестков на цветах, виды плодов и бабочек, спирали раковин, строение многогранных кристаллов и т.п. Строение самого человеческого тела тоже симметрично. Зачатки учения о симметрии относятся к глубокой древности — об этом свидетельствуют разнообразные геометрические орнаменты на сохранившихся от той эпохи каменных и гранитных плитах и сосудах. Многовековые наблюдения человека над симметричными фигурами среди минералов, растений и животных, его долголетний опыт применения симметрии в строительстве и искусстве привели к созданию учения о симметрии. О ней писал в своем трактате «Об архитектуре» римский инженер Витрувий(I в.), ее изучали и применяли архитекторы и художники эпохи Возрождения, в том числе выдающиеся итальянские живописцы Леонардо да Винчи и Рафаэль; ею занимались ученые нового времени Луи Пастер (1822-1895), Пьер и Жак Кюри и другие. В геометрию элементы учения о симметрии ввел французский математик А. М. Лежандр (1752-1833). В настоящее время учение о симметрии лежит в основе кристаллографии и находит широкое применение в науке, технике и промышленности.         

Движения систематически применялись пифагорейцами ,которые рассматривали линии как следы движущихся точек, а поверхности -как следы движущихся линий.  Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся  погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров (своего рода «палетка»). Пропорциональность отрезков, образующихся на прямых пересеченных несколькими параллельными прямыми, была известна еще вавилонским ученым, хотя некоторые приписывают это открытие Фалесу Милетскому. До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов. Учение о подобии фигур на основе теории отношений и пропорции было создано в древней Греции в V-IV вв. до н. э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и других. Оно изложено в 6 книге «Начал» Евклида, начинающейся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».

        Признаки подобия треугольников доказываются в наших учебниках иначе, чем у Евклида, и основываются на лемме о том, что в любом треугольнике прямая, параллельная основанию, пересекающая стороны треугольника, отсекает треугольник, подобный данному. Эта лемма была впервые введена Клавиус м в его комментариях к «Началам» Евклида, изданным в 1574 году. Она, как и вся теория подобия ,основывается на аксиоме параллельности Евклида.  Интерес к векторам и векторному исчислению пробудился у математиков в XIX веке в связи с потребностями механики и физики.  Однако истоки исчисления с направленными отрезками возникли еще в древней Греции у пифагорейцев, которые пытались свести вопросы арифметики и алгебры к решению задач геометрическим путем. В «Началах» Евклида векторное исчисление получило дальнейшее развитие(сложение и вычитание векторов). В 1587 году фламандский ученый С. Ставин в своем труде «Начала статики» ввел сложение двух векторов, перпендикулярных друг другу. Продолжительное время вектор рассматривался только как направленный отрезок ,один из концов которого называли началом, а другой — его концом.  С разработкой теории преобразований вектор стали рассматривать не только как направленный отрезок, но и как параллельный перенос, заданный парой точек — точкой О и ее образом О’.

        Гомотетия встречается, по-видимому, впервые в трактате Апполония «О плоских местах», о содержании которого сообщает александрийский математик III в. н. э. Папп в своем «Математическом собрании».