Конспект «Действие магнитного поля на проводник с током»

«Действие магнитного поля на проводник с током»

---

---

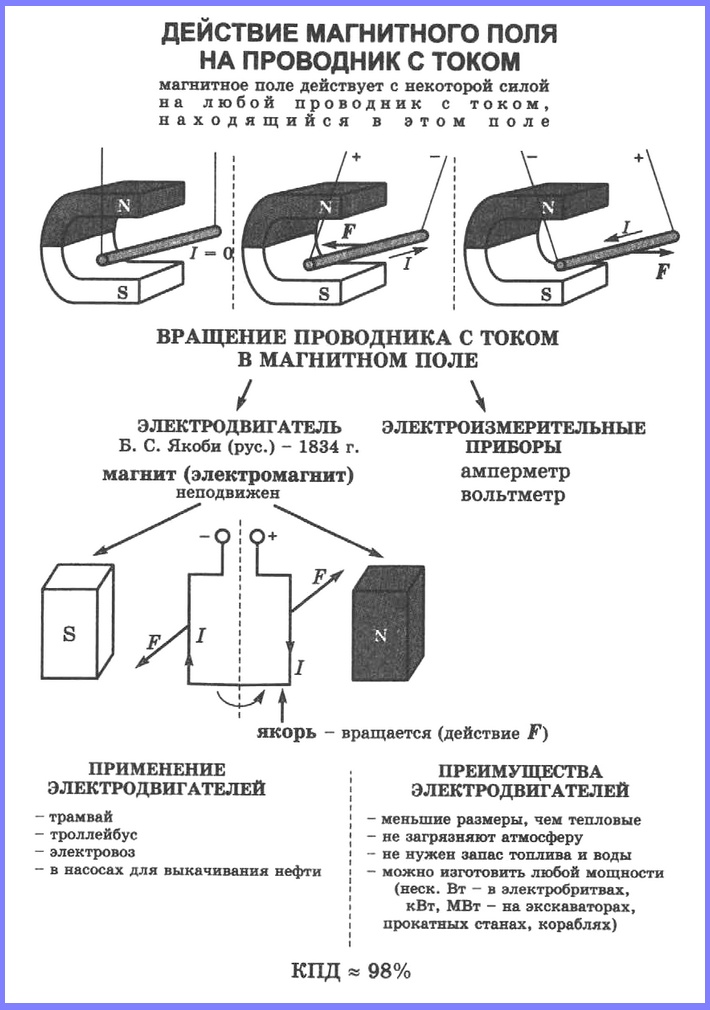
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.

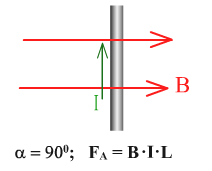
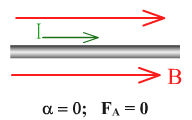
Сила Ампера зависит от длины проводника с током, силы тока в проводнике, модуля магнитной индукции и расположения проводника относительно линий магнитной индукции: F_A = BIlsinа.

Для определения направления силы Ампера применяют правило левой руки. Если левую руку расположить в магнитном поле так, чтобы силовые линии входили в ладонь, а четыре пальца были направлены по току, то отогнутый большой палец укажет направление силы, действующей на проводник.

Магнитное взаимодействие можно наблюдать между двумя параллельными токами (опыт Ампера): два параллельных проводника с током отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают.

Экспериментальное исследование показывает, что сила Ампера прямо пропорциональна длине проводника l и силе тока I в проводнике. Коэффициентом пропорциональности в этом равенстве является модуль вектора магнитной индукции В. Соответственно, F = BIl. В таком виде зависимость силы, действующей на проводник с током в магнитном поле, записывается в том случае, если линии магнитной индукции перпендикулярны проводнику с током. Из приведённой формулы понятно, что магнитная индукция является силовой характеристикой магнитного поля.

Единица магнитной индукции [В] =  1Н / 1А • 1м = 1 Тл. За единицу магнитной индукции принимают магнитную индукцию такого поля, в котором на проводник длиной 1 м действует сила 1Н при силе тока в проводнике 1 А

.

Магнитное поле действует также на движущиеся заряженные частицы. При этом сила (сила Лоренца) зависит от модуля магнитной индукции, заряда частицы, а также от модуля и направления её скорости.

Электрический двигатель

Движение проводника с током в магнитном поле лежит в основе работы электрического двигателя. Если поместить прямоугольную рамку в магнитное поле и пропустить по ней электрический ток, то рамка повернётся, потому, что на стороны рамки действует сила Ампера. При этом сила, действующая на сторону рамки ab, противоположна силе, действующей на сторону cd.

Для того чтобы рамка не остановилась в тот момент, когда её плоскость перпендикулярна линиям магнитной индукции, и продолжала вращаться, изменяют направление тока в проводнике. Для этого к концам рамки припаяны полукольца, по которым скользят контакты, соединённые с источником тока. При повороте рамки на 180° меняются контактные пластины, которых касаются полукольца и, соответственно, направление тока в рамке.

В электрическом двигателе энергия электрического и магнитного полей превращается в механическую энергию.

 

---

Действие магнитного поля на проводник с током

---

Конспект урока по физике в 8 классе «Действие магнитного поля на проводник с током».

Следующая тема: «Электромагнитная индукция. Опыты Фарадея».

 

Действие магнитного поля на движущийся электрический заряд

Если бы Андре Мари Ампер (рис. 1) знал о действии электрического тока, то продвинулся бы гораздо дальше в своих открытиях.

Рис. 1. Андри Мари Ампер (Источник)

Как и многие ученые того периода, Ампер придерживался «модели эфира»: электрический ток – эфир, некая жидкость, которая протекает по проводникам. Именно отсюда и сам термин «электрический ток» – то, что течет. Только в самом конце XIX века – начале ХХ модели эфиров стали отходить, а на смену им стали появляться новые модели, адекватнее отражающие наблюдаемые явления. В частности, были открыты катодные лучи, была выявлена радиоактивность, проведены исследования Фарадея по электролизу – все это наводило на мысль о существовании заряженных частиц, которые как-то движутся.

Ученый Хендрик Лоренц (рис. 2) предложил так называемую «электронную модель» металлов.

Рис. 2. Хендрик Лоренц (Источник)

При образовании кристаллической решетки металлов от каждого атома металла отрывается по одному внешнему электрону, таким образом, в узлах кристаллической решетки находятся положительные ионы, а в объеме этой решетки почти свободно могут двигаться электроны (рис. 3).

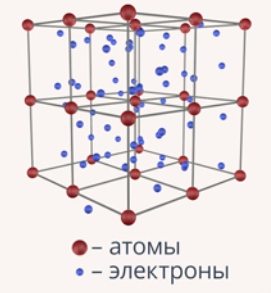
Рис. 3. Кристаллическая решетка

Модель, предложенная Лоренцом, была хороша хотя бы тем, что достаточно легко объясняла возникновение электрического тока в металлах. При обычных условиях эти электроны находятся в беспорядочном движении вокруг кристаллической решетки. И только при подаче разности потенциалов на конце проводника, когда внутри проводника появляется электрическое поле, кроме этой хаотической составляющей появляется другая – упорядоченная составляющая, или направленное движение. Именно это движение, согласно модели Лоренца, представляет собой электрический ток.

Вы знаете, что стороны магнитного поля (B) на проводник с током (

I) действует сила Ампера (F), перпендикулярная направлению тока и направлению линий магнитного поля (рис. 4).

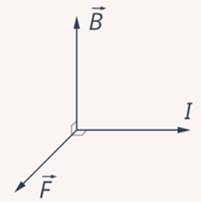
Рис. 4. Направление силы Ампера

«Если электрический ток представляет собой направленное движение зарядов, то не будет ли со стороны магнитного поля действовать такая же сила на сами заряды?» – примерно так рассуждал Лоренц. В выражение для силы Ампера вместо силы тока подставим определение силы тока – отношение перенесенного заряда в проводнике ко времени, за которое было осуществлено данное перенесение:

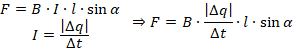
Также заметим, что отношение элемента длины проводника к интервалу времени – скорость движения заряда:

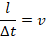
Тогда выражение принимает вид:

Модуль силы равен произведению величины магнитной индукции поля на количество переносимого через проводник заряда на скорость частиц, которые переносят заряд и на синус угла между направлением движения заряда и направлением вектора магнитной индукции.

Учтем, что носителями электрического тока в проводнике являются электроны, величина зарядов которых одинакова. Поэтому можно записать, что совокупный заряд, переносимый через поперечное сечение проводника, – произведение заряда электрона q на количество электронов N, переносимых через поперечное сечение проводника.

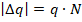
Тогда:

Вывод приведенной формулы был сугубо формальным, однако даже такой вывод позволял предположить, что не только на проводник с током, но и на отдельный заряд в магнитном поле будет действовать сила со стороны этого поля. Предположим, что число зарядов равно единице и этот заряд движется не внутри кристаллической решетки, а в свободном пространстве. Возникает вопрос: что произойдет с этим зарядом, если он войдет в область, где существует однородное магнитное поле? Согласно нашей гипотезе, на частицу, движущуюся в однородном магнитном поле, должна действовать сила, которая перпендикулярна скорости этой частицы (поскольку именно так будет направлен электрический ток, связанный с движением этих частиц) и перпендикулярна линиям магнитного поля (рис. 5).

Рис. 5. Направление действия силы на движущийся заряд

Величина этой силы будет определяться так:

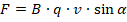
Открытие катодных лучей, а также радиоактивности позволили проверить экспериментально гипотезу Лоренца. Воспользуемся электронно-лучевой трубкой.

В вакуумной трубке размещены две пластины: анод и катод. На катод подается отрицательный потенциал, на анод – положительный. Для того чтобы в трубке возникли свободные электроны, катод нагревается нитью накала. Свободные электроны металлического катода вблизи его поверхности могут покидать эту поверхность, обладая высокой кинетической энергией за счет нагревания – явление термоэлектронной эмиссии. Свободные электроны, покинувшие поверхность катода, попадают в зону действия электрического поля между анодом и катодом. Линии напряженности этого поля направлены от анода к катоду (изображены белыми стрелками). Электроны, будучи отрицательно заряженными частицами, движутся от катода к аноду – против линии напряженности поля (направление движения изображено красными стрелками). Так, в трубке возникает электрический ток, направленный от анода к катоду (рис. 6).

Рис. 6. Электронно-лучевая трубка

Если использовать экран, покрытый специальным материалом, который светится при попадании на него заряженных частиц, можно пронаблюдать место попадания электронов по световому пятну. Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зеленое пятно на экране – это место бомбардировки экрана электронами (рис. 7).

Рис. 7. Работа электронно-лучевой трубки

Воспользуемся осциллографом. Для удобства будем следить не за световым пятном, а за светящейся линией (рис. 8).

Рис. 8. Светящаяся линия на экране осциллографа

Когда одним из полюсов подводят к горизонтальной линии, находящейся на осциллографе, она отклоняется от своего первоначального значения в направлении, перпендикулярном направлению скорости и направлению линий магнитного поля, поскольку магнитное поле направлено от северного полюса к южному. Это на качественном уровне подтверждает гипотезу (рис. 9).

  

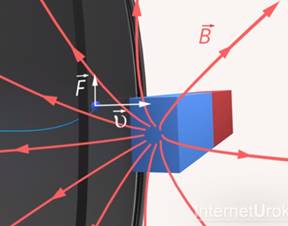
Рис. 9. Отклонения электронов в электронно-лучевой трубке

Попытаемся получить не только качественные, но и количественные результаты. Для этого будем проверять зависимость силы, действующей со стороны магнитного поля, от различных факторов. В частности, от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия, тем быстрее движутся электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов, то по мере уменьшения яркости искажение линии также будет уменьшаться (рис. 10). Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды, и скоростью этих зарядов.

Рис. 10. При уменьшении яркости искажение линии уменьшается

Сила, действующая на заряды со стороны магнитного поля, пропорциональна индукции – если поднести несколько магнитов к осциллографу, то искажение будет гораздо сильнее.

Рис. 11. При усилении магнитного поля искажение линии увеличивается

Величина силы действующей со стороны магнитного поля на движущийся заряд зависит от взаимного направления вектора магнитной индукции и вектора скорости движения частиц. При поднесении магнитов к осциллографу южным полюсом линия будет искажаться в противоположном направлении.

Рис. 12. При поднесении магнитов южным полюсом линия искажается в противоположном направлении

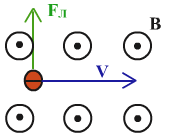
Обобщим выводы из проделанных экспериментов. На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения (v) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции. Направление силы определяется по правилу «левой руки».

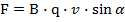
Таким образом, полученное ранее выражение для силы описывает взаимодействие магнитного поля с движущимся в этом поле электрическим зарядом. Открытие силы действия магнитного поля на движущийся в нем заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название сила Лоренца.

Сделаем еще несколько замечаний.

1. Вектор силы Лоренца перпендикулярен вектору скорости:

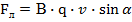
2. Если сила перпендикулярна вектору скорости, то она называется центростремительной. Под ее действием тело движется по окружности. Следовательно, сила Лоренца – центростремительная сила.

3. Под действием силы Лоренца заряд движется по дуге окружности, следовательно, он обладает центростремительным ускорением. Центростремительное ускорение может быть рассчитано как квадрат скорости движения, деленный на радиус окружности, который описывает тело:

 

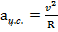
4. Согласно второму закону Ньютона, сила может быть определена как произведение массы тела на приобретаемое им ускорение:

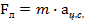
Подставив выражения для силы Лоренца, получим:

 

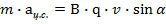
Подставим выражение для центростремительного ускорения:

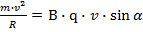   (1.14)

После сокращения скорости получим следующие соотношения:

 

  

  

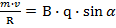
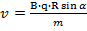
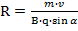
Список литературы

1. Касьянов В.А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл.
2. Степанова Г.Н. Физика 11. – М.: Русское слово.
3. Пурышева Н.С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М. Физика 11. – М.: Дрофа.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «Fizika.in» (Источник).
2. Интернет-портал «Классная физика» (Источник).
3. Интернет-портал «Balancer.ru» (Источник).

 

Домашнее задание

1. Касьянов В.А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.
2. Какая сила действует на протон, который движется со скоростью 2 ∙ 10⁶ м/с в однородном магнитном поле с индукцией 0,1 Тл? Протон движется под углом 60° по отношению к линиям магнитной индукции поля.
3. На рис. 13 и 14 схематически показаны разные случаи взаимодействия заряженной частицы, которая движется, и магнитного поля. Сформулируйте задачу в каждом случае и решите ее.

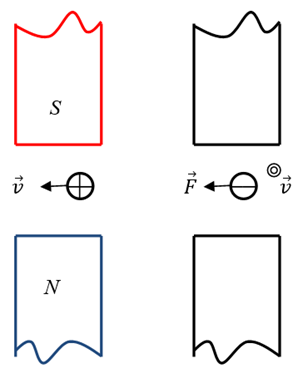
Рис. 13

Рис. 14

4. ^*Электрон, который влетел в однородное магнитное поле под углом 60° по отношению к линиям магнитной индукции, двигается по винтовой линии радиусом 2 см, делая один оборот за 30 нс. Определите магнитную индукцию поля и шаг винтовой линии.

2.Магнитное поле. Действие магнитного поля на электрические заряды (продемонстрировать опыты, подтверждающие это действие).

Магнитное поле– это особая форма материи, существующая независимо от нас и от наших знаний о нём. Оно обладает следующими свойствами:

1. возникает вокруг движущихся зарядов и проводников с током;

2. действует на движущиеся заряды и проводники с током.

Силовой характеристикой магнитного поля является магнитная индукция.

Модулем магнитной индукцииназывается отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.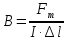, гдеB– модуль магнитной индукции,F_mмаксимальная сила,Iсила тока, ∆l – длина проводника.

Магнитная индукция измеряется в Теслах(Тл).

Магнитная индукция – векторная величина.

Вектор направлен от северного полюса магнита к южному полюсу.

Для прямолинейного проводника с током направление 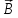вектора определяют поправилубуравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения буравчика совпадёт с направлением вектора.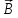

Сила, действующая со стороны магнитного поля на проводник с током, называется силойАмпера.

Сила Ампера вычисляется по формул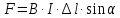е: , где.

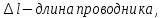
Сила, действующая со стороны магнитного поля на движущийся заряд, называется силой Лоренца.

Сила Лоренца вычисляется по формул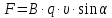е: , где.

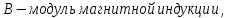
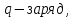
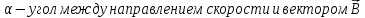Направление силы Ампера и силы Лоренца определяется по правилу левой руки.

Для демонстрации действия магнитного поля на движущиеся заряды (электрический ток) необходимо подключить проволочный моток к источнику тока и, поднося к нему магнит разными полюсами, показать отталкивание и притяжение мотка.

3.Задача на применение графиков изопроцессов.

Билет № 14

1.Фотоэффект и его законы. Уравнение Эйнштейна для фотоэффекта. Применение фотоэффекта в технике.

Фотоэффект– это вырывание электронов из вещества под действием света.

Фотоэффект был открыт в 1887 г. немецким физиком Герцем и изучался экспериментально русским учёным Столетовым.

Столетов в опытах использовал стеклянный вакуумный баллон со впаянными в него двумя электродами. На электроды подавалось напряжение, а отрицательный электрод освещался светом. Под действием света из электрода вырывались электроны, которые двигались ко второму электроду. Т.е. создавался электрический ток.

В результате опытов Столетов получил следующие законы:

1.Количество электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны.

2.Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.

Объяснение фотоэффекта было дано в 1905 г. Эйнштейном.

Он использовал гипотезу немецкого физика Планка: свет излучается и поглощается отдельными порциями – квантами.

По Эйнштейну: свет – поток особых частиц – фотонов. Энергия фотона:E = h·ν, где h– постоянная Планка,ν– частота света.

Уравнение Эйнштейна: энергия порции светаидёт на совершение работы выхода электрона из металла и на сообщение электрону кинетической энергии.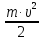

Приборы, в основе действия которых лежит фотоэффект, называются фотоэлементами.

Они используются в кино для воспроизведения звука, в фотометрии для измерения освещённости, в калькуляторах, в солнечных батареях и т.д.

Опыт Эрстеда. Магнитное поле тока. Взаимодействие магнитов. Действие магнитного поля на проводник с током

1. Опыт Эрстеда заключается в следующем. На столе располагают магнитную стрелку, которая ориентируется с севера на юг в магнитном поле Земли, и параллельно ей сверху проводник, соединённый с источником тока (см. рис. 81). При замыкании цепи стрелка повернётся на 90° и встанет перпендикулярно проводнику.

При размыкании цепи стрелка вернётся в первоначальное положение. Если изменить направление тока на противоположное, то стрелка повернётся в обратную сторону. Опыт Эрстеда доказывает, что вокруг проводника, по которому течёт электрический ток, существует магнитное поле, которое действует на магнитную стрелку.

Опыт Эрстеда показал существование взаимосвязи между электрическими и магнитными явлениями.

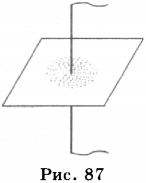
Об этой взаимосвязи свидетельствует и опыт, известный как опыт Ампера. Если по двум длинным параллельно расположенным проводникам пропустить электрический ток в одном направлении, то они притянутся друг к другу; если направление тока будет противоположным, то проводники оттолкнутся друг от друга. Это происходит потому, что вокруг одного проводника возникает магнитное поле, которое действует на другой проводник с током. Если ток будет протекать только по одному проводнику, то проводники не будут взаимодействовать.

Таким образом, вокруг движущихся электрических зарядов или вокруг проводника с током существует магнитное поле. Магнитное поле действует на движущиеся заряды. На неподвижные заряды магнитное поле не действует.

Силовой характеристикой магнитного поля является величина, называемая магнитной индукцией. Обозначается магнитная индукция буквой ​\( B \)​. Магнитная индукция является векторной величиной, т.е. имеет определённое направление. Это наглядно проявляется в опыте со взаимодействием параллельных проводников с током. Направление вектора магнитной индукции совпадает с направлением северного полюса магнитной стрелки в данной точке поля.

2. Обнаружить магнитное поле вокруг проводника с током можно с помощью либо магнитных стрелок, либо железных опилок, которые в магнитном поле намагничиваются и становятся магнитными стрелками. На рисунке 87 изображён проводник, пропущенный через лист картона, на который насыпаны железные опилки. При прохождении по проводнику электрического тока опилки располагаются вокруг него по концентрическим окружностям.

Линии, вдоль которых располагаются в магнитном поле магнитные стрелки или железные опилки, называют линиями магнитной индукции. Направление, которое указывает северный полюс магнитной стрелки, принято за направление линий магнитной индукции. Вектор магнитной индукции направлен по касательной к линии магнитной индукции в каждой точке поля.

Как следует из результатов опыта Эрстеда и опыта по взаимодействию параллельных проводников с током, направление линий вектора магнитной индукции (и линий магнитной индукции) зависит от направления тока в проводнике. Направление линий магнитной индукции можно определить с помощью правила буравчика. Для линейного проводника оно следующее: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитной индукции.

3. Если пропустить электрический ток по катушке, то опилки расположатся, как показано на рисунке 88.

Картина линий магнитной индукции свидетельствует о том, что катушка с током становится магнитом. Если катушку с током подвесить, то она повернётся южным полюсом на юг, а северным — на север (рис. 89).

Следовательно, катушка с током имеет два полюса: северный и южный. Определить полюса, которые появляются на её концах можно, если известно направление электрического тока в катушке. Для этого пользуются правилом буравчика: если направление вращения ручки буравчика совпадает с направлением тока в катушке, то направление поступательного движения буравчика совпадает с направлением линий магнитной индукции внутри катушки (рис. 90).

4. Тела, длительное время сохраняющие магнитные свойства, или намагниченность, называют постоянными магнитами. Поднося магнит к железным опилкам, можно заметить, что они притягиваются к концам магнита и практически не притягиваются к его середине. Те места магнита, которые производят наиболее сильное магнитное действие, называются полюсами магнита. Магнит имеет два полюса: северный — N и южный — S. Принято северный полюс магнита окрашивать синим цветом, а южный — красным. Если полосовой магнит разделить на две части, то каждая из них окажется магнитом с двумя полюсами.

Положив на постоянный магнит лист бумаги или картона и насыпав на него железные опилки, можно получить картину его магнитного поля (рис. 91). Линии магнитной индукции постоянных магнитов замкнуты, все они выходят из северного полюса и входят в южный, замыкаясь внутри магнита.

Магнитные стрелки и магниты взаимодействуют между собой. Разноимённые магнитные полюсы притягиваются друг к другу, а одноимённые — отталкиваются. Взаимодействие магнитов объясняется тем, что магнитное поле одного магнита действует на другой магнит и, наоборот, магнитное поле 2-го магнита действует на 1-й.

Причиной наличия у веществ магнитных свойств является движение электронов, существующих в каждом атоме. При своём движении вокруг атома электроны создают магнитные поля. Если эти поля имеют одинаковую ориентацию, то вещество, например железо или сталь, намагничены достаточно сильно.

5. Магнитное поле действует на проводник с током. Доказать это можно с помощью эксперимента (рис. 92).

Если в поле подковообразного магнита поместить проводник длиной ​\( l \)​, подвешенный на тонких проводах, соединить его с источником тока, то при разомкнутой цепи проводник останется неподвижным. Если замкнуть цепь, то по проводнику пойдёт электрический ток, и проводник отклонится в магнитном поле от своего первоначального положения. При изменении направления тока проводник отклонится в противоположную сторону. Таким образом, на проводник с током, помещённый в магнитное поле, действует сила, которую называют силой Ампера.

Экспериментальное исследование показывает, что сила Ампера прямо пропорциональна длине проводника ​\( l \)​ и силе тока ​\( I \)​ в проводнике: ​\( F\sim Il \)​. Коэффициентом пропорциональности в этом равенстве является модуль вектора магнитной индукции ​\( B \)​. Соответственно, ​\( F=BIl \)​.

Сила, действующая на проводник с током, помещённый в магнитное поле, равна произведению модуля вектора магнитной индукции, силы тока и длины той части проводника, которая находится в магнитном поле.

В таком виде зависимость силы, действующей на проводник с током в магнитном поле, записыватся в том случае, если линии магнитной индукции перпендикулярны проводнику с током.

Формула силы Ампера, позволяет раскрыть смысл понятия вектора магнитной индукции. Из выражения для силы Ампера следует: ​\( B=\frac{F}{Il} \)​, т.е. магнитной индукцией называется физическая величина, равная отношению силы, действующей на проводник с током в магнитном поле, к силе тока и длине проводника, находящейся в магнитном поле.

Из приведённой формулы понятно, что магнитная индукция является силовой характеристикой магнитного поля.

Единица магнитной индукции ​\( [В] = [F]/[I][l] \)​. ​\( [B] \)​ = 1 Н/(1 А · 1 м) — 1 Н/(А · м) = 1 Тл. За единицу магнитной индукции принимают магнитную индукцию такого поля, в котором на проводник длиной 1 м действует сила 1 Н при силе тока в проводнике 1 А.

Направление силы Ампера определяют, пользуясь правилом левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца направлены по направлению тока в проводнике, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник (рис. 93).

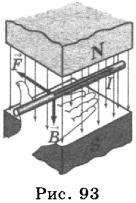
6. Движение проводника с током в магнитном поле лежит в основе работы электрического двигателя. Если поместить прямоугольную рамку в магнитное поле и пропустить по ней электрический ток, то рамка повернётся (рис. 94), потому, что на стороны рамки действует сила Ампера. При этом сила, действующая на сторону рамки ​\( ab \)​, противоположна силе, действующей на сторону ​\( cd \)​.

Для того чтобы рамка не остановилась в тот момент, когда её плоскость перпендикулярна линиям магнитной индукции, и продолжала вращаться, изменяют направление тока в проводнике. Для этого к концам рамки припаяны полукольца, по которым скользят контакты, соединённые с источником тока. При повороте рамки на 180° меняются контактные пластины, которых касаются полукольца и, соответственно, направление тока в рамке.

В электрическом двигателе энергия электрического и магнитного полей превращается в механическую энергию.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. На рисунке показано, как установилась магнитная стрелка между полюсами двух одинаковых магнитов. Укажите полюса магнитов, обращённые к стрелке.

1) 1 — S, 2 — N
2) 1 — А, 2 — N
3) 1 — S, 2 — S
4) 1 — N, 2 — S

2. Па рисунке представлена картина линий магнитного поля от двух полосовых магнитов, полученная с помощью магнитной стрелки и железных опилок. Каким полюсам полосовых магнитов соответствуют области 1 и 2?

1) 1 — северному полюсу; 2 — южному
2) 1 — южному; 2 — северному полюсу
3) и 1, и 2 — северному полюсу
4) и 1, и 2 — южному полюсу

3. При прохождении электрического тока по проводнику магнитная стрелка, находящаяся рядом, расположена перпендикулярно проводнику. При изменении направления тока на противоположное. Стрелка

1) повернётся на 90°
2) повернётся на 180°
3) повернётся на 90° или на 180° в зависимости от значения силы тока
4) не изменит свое положение

4. Проводник, по которому протекает электрический ток, расположен перпендикулярно плоскости чертежа (см. рисунок). Расположение какой из магнитных стрелок, взаимодействующих с магнитным полем проводника с током, показано правильно?

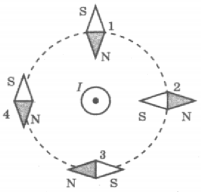
1) 1
2) 2
3) 3
4) 4

5. Из проводника сделали кольцо и по нему пустили электрический ток. Ток направлен против часовой стрелки (см. рисунок). Как направлен вектор магнитной индукции в центре кольца?

1) вправо
2) влево
3) на нас из-за плоскости чертежа
4) от нас за плоскость чертежа

6. По катушке идёт электрический ток, направление которого показано на рисунке. При этом на концах железного сердечника катушки

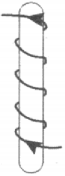
1) образуются магнитные полюса — на конце 1 — северный полюс, на конце 2 — южный
2) образуются магнитные полюса — на конце 1 — южный полюс, на конце 2 — северный
3) скапливаются электрические заряды: на конце 1 — отрицательный заряд, на конце 2 — положительный
4) скапливаются электрические заряды: на конце 1 — положительный заряд, на конце 2 — отрицательный

7. Два параллельно расположенных проводника подключили параллельно к источнику тока.

Направление электрического тока и взаимодействие проводников верно изображены на рисунке

8. В однородном магнитном поле на проводник с током, расположенный перпендикулярно плоскости чертежа (см. рисунок), действует сила, направленная

1) вправо →
2) влево ←
3) вверх ↑
4) вниз ↓

9. Сила, действующая на проводник с током, который находится в магнитном поле между полюсами магнита направлена

1) вверх ↑
2) вниз ↓
3) направо →
4) налево ←

10. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?

1) вверх ↑
2) вправо →
3) вниз ↓
4) влево ←

11. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Вокруг неподвижных зарядов существует магнитное поле.
2) Вокруг неподвижных зарядов существует электростатическое поле.
3) Если разрезать магнит на две части, то у одной части будет только северный полюс, а у другой — только южный.
4) Магнитное поле существует вокруг движущихся зарядов.
5) Магнитная стрелка, находящаяся около проводника с током, всегда поворачивается вокруг своей оси.

12. Электрическая схема содержит источник тока, проводник АВ, ключ и реостат. Проводник АВ помещён между полюсами постоянного магнита (см. рисунок).

Используя рисунок, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) При перемещении ползунка реостата влево сила Ампера, действующая на проводник АВ, увеличится.
2) При замкнутом ключе проводник будет выталкиваться из области магнита вправо.
3) При замкнутом ключе электрический ток в проводнике имеет направление от точки В к точке А.
4) Магнитные линии поля постоянного магнита в области расположения проводника АВ направлены вертикально вниз.
5) Электрический ток, протекающий в проводнике АВ, создаёт однородное магнитное поле.

Часть 2

13. Участок проводника длиной 0,1 м находится в магнитном поле индукцией 50 мТл. Сила тока, протекающего по проводнику, 10 А. Какую работу совершает сила ампера при перемещении проводника на 8 см в направлении своего действия? Проводник расположен перпендикулярно линиям магнитной индукции.

Ответы

Опыт Эрстеда. Магнитное поле тока. Взаимодействие магнитов. Действие магнитного поля на проводник с током

Оценка

Действие магнитного поля » как устроен и работает постоянный магнит.

 

 

 

Тема: магнитное поле, его принцип действия постоянного магнита.

 

Силовые поля представляют собой особый вид материи, одной из разновидностей является магнитное поле. О его действии знает практически каждый человек. Ведь кто не сталкивался с обычными постоянными магнитиками? Вряд ли найдётся такой человек в современном обществе. А знаете ли вы, что именно наделяет магниты их специфическим действием? Думаю, не многим это известно. Предлагая сделать небольшой теоретическое путешествие в устройство и принцип действия постоянного магнита, и наконец разобраться, что же там такое происходит, почему это работает именно таким образом.

 

Действие магнитного поля лежит в основе электрофизики. Как известно, любые вещества состоят из атомов. Они находятся на очень близком расстоянии друг к другу. В зависимости от жёсткости соединения между собой различают три базовых агрегатных состояния — твёрдое, жидкое и газообразное. Именно в твёрдом состоянии вещества атомы максимально плотно и жёстко прикреплены друг у другу, что составляет в целом кристаллическую решётку того или иного вещества. Также известно, что атомы состоят из более мелких частиц, которые своим строением похожи на солнечную систему (в центре располагается солнце-атом, а вокруг него вращаются электроны-планеты). Между частицами атома также существуют поля.

 

Ну со строением вещества разобрались, а где тут действие магнитного поля, спросите вы. А оно имеет хитрый принцип действия. Основы физики утверждают, что магнитное поле возникает вокруг движущихся заряженных частиц (электронов, ионов). Каждый атом содержит определённое количество электронов на своих орбитах, они быстро вращаются вокруг ядра атома. Следовательно вокруг каждого атома существует магнитное поле. Но если все вещества состоят из атомов, то почему далеко не все вещества обладают магнитными свойствами? Потому, что именно некоторые вещества в твёрдом состоянии обладают особенностью перенаправлять и запоминать вектор направленности магнитного поля.

 

 

 

 

Итак, в изначальном состоянии тела (обладающее магнитными свойствами) внутренние векторы направления магнитных полей атомов располагаются хаотичным образом, что ведёт к взаимной нейтрализации общего действия магнитного поля. А вот если внешним мощным постоянным магнитным полем одновременно развернуть все внутренние составляющие магнитных полей, то в результате мы получим действие магнитного поля, которое будет уже однонаправленным.

 

Проще говоря, вещества, обладающие магнитными свойствами, могут запоминать направление магнитных полей, которые исходят от внутренних элементарных частиц. Если в изначальном состоянии внутренние магнитные поля направлены хаотично, компенсируя друг друга, то при мощном воздействии внешнего магнитного поля все внутренние поля перестраиваются в одном направлении (оставаясь в нём постоянно).

 

Если до воздействия внешнего магнитного поля вещество не магнитило к себе металлические предметы, то после этого оно уже само стало постоянным магнитом. Действие магнитного поля стало проявляться в силу обычной внутренней перестройки элементарных частиц.

 

Данное явление имеет и обратный процесс. А именно, получившийся постоянный магнит можно вернуть обратно в исходное состояние (оно обратно утратит способность магнитить). Для этого лишь надо перестроить в хаотичный порядок внутреннюю структуру магнетика. Вещество можно сильно нагреть, подвергнуть воздействию механических ударов, поместить в переменное электромагнитное поле и т.д.

 

P.S. Помимо обычного развлечения магниты имеют огромную область своего использования. Если в доме постоянные магнитики используются для крепления записок на холодильник, то в технике они стоят в основе многих электротехнических систем и устройств (постоянные двигатели, генераторы, электромеханические измерительные устройства и т.д.).

Магнитное поле Земли — Википедия

Обтекание магнитосферы Земли солнечным ветром

Магни́тное по́ле Земли́ или геомагни́тное по́ле — магнитное поле, генерируемое внутриземными источниками. Предмет изучения геомагнетизма. Появилось 4,2 млрд лет назад^[1].

Строение и характеристики магнитного поля Земли[править | править код]

Собственное магнитное поле Земли (геомагнитное поле) можно разделить на cледующие основные части^[2]:

• главное поле,
• поля мировых аномалий,
• внешнее магнитное поле.

Главное поле[править | править код]

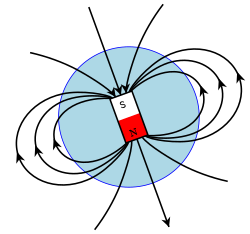Земля как магнитный диполь.

Более чем на 90 % оно состоит из поля, источник которого находится внутри Земли, в жидком внешнем ядре, — эта часть называется главным, основным или нормальным полем^[3][4][5]. Оно аппроксимируется в виде ряда по гармоникам — ряда Гаусса, а в первом приближении вблизи поверхности Земли (до трёх её радиусов) близко к полю магнитного диполя, то есть имеет такой вид, как будто земной шар представляет собой полосовой магнит с осью, направленной приблизительно с севера на юг^{[2][6][3][7][8]}. Центр этого диполя смещен относительно центра Земли, а ось наклонена к оси вращения Земли на угол около 10°. На такой же угол отстоят от соответствующих географических полюсов геомагнитные полюса — точки пересечения оси диполя с поверхностью Земли^[4]. Их положение в различные моменты времени вычисляется в рамках той или иной модели магнитного поля, определяющей тем или иным образом первые три коэффициента в ряду Гаусса^[3]. Эти глобальные модели, такие как Международное геомагнитное аналитическое поле (International Geomagnetic Reference Field, IGRF)^[9] и Всемирная магнитная модель (World Magnetic Model, WMM)^[en][10], создаются различными международными геофизическими организациями, и каждые 5 лет утверждаются и публикуются обновлённые наборы коэффициентов Гаусса, определяющих все данные о состоянии геомагнитного поля и его параметрах^[4]. Так, согласно модели WMM2015, северный геомагнитный полюс (по сути это южный полюс магнита) имеет координаты 80,37° с. ш. и 72,62° з. д., южный геомагнитный полюс — 80,37° ю. ш., 107,38° в. д., наклон оси диполя относительно оси вращения Земли — 9,63°^[3][11].

Поля мировых аномалий[править | править код]

Реальные силовые линии магнитного поля Земли, хотя в среднем и близки к силовым линиям диполя, отличаются от них местными нерегулярностями, связанными с наличием намагниченных пород в коре, расположенных близко к поверхности. Из-за этого в некоторых местах на земной поверхности параметры поля сильно отличаются от значений в близлежащих районах, образуя так называемые магнитные аномалии^[2][4][7][8]. Они могут накладываться одна на другую, если вызывающие их намагниченные тела залегают на разных глубинах^[5].

Существование магнитных полей протяжённых локальных областей внешних оболочек приводит к тому, что истинные магнитные полюса — точки (вернее, небольшие области), в которых силовые линии магнитного поля абсолютно вертикальны, — не совпадают с геомагнитными, при этом они лежат не на самой поверхности Земли, а под ней^[4][3][6]. Координаты магнитных полюсов на тот или иной момент времени также вычисляются в рамках различных моделей геомагнитного поля путём нахождения итеративным методом всех коэффициентов в ряду Гаусса. Так, согласно актуальной модели WMM, в 2015 г. северный магнитный полюс находился в точке 86° с. ш., 159° з. д., а южный — 64° ю. ш., 137° в.д^[3]. Значения актуальной модели IGRF12 немного отличаются: 86,3° с. ш., 160° з. д., для северного полюса, 64,3° ю. ш., 136,6° в.д для южного^[11].

Соответственно, магнитная ось — прямая, проходящая через магнитные полюса, — не проходит через центр Земли и не является её диаметром^[6][7].

Положения всех полюсов постоянно смещаются — геомагнитный полюс прецессирует относительно географического с периодом около 1200 лет^[2].

Внешнее магнитное поле[править | править код]

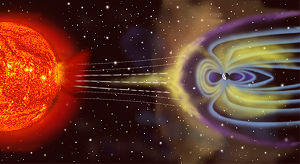
Оно определяется источниками в виде токовых систем, находящимися за пределами земной поверхности, в её атмосфере^[2][4]. В верхней части атмосферы (100 км и выше) — ионосфере — её молекулы ионизируются, формируя плотную холодную плазму, поднимающуюся выше, поэтому часть магнитосферы Земли выше ионосферы, простирающаяся на расстояние до трёх её радиусов, называется плазмосферой. Плазма удерживается магнитным полем Земли, но её состояние определяется его взаимодействием с солнечным ветром — потоком плазмы солнечной короны^[12].

Таким образом, на большем удалении от поверхности Земли магнитное поле несимметрично, так как искажается под действием солнечного ветра: со стороны Солнца оно сжимается, а в направлении от Солнца приобретает «шлейф», который простирается на сотни тысяч километров, выходя за орбиту Луны^[2]. Эта своеобразная «хвостатая» форма возникает, когда плазма солнечного ветра и солнечных корпускулярных потоков как бы обтекают земную магнитосферу — область околоземного космического пространства, ещё контролируемую магнитным полем Земли, а не Солнца и других межпланетных источников^[2][4][7][8]; она отделяется от межпланетного пространства магнитопаузой, где динамическое давление солнечного ветра уравновешивается давлением собственного магнитного поля. Подсолнечная точка магнитосферы в среднем находится на расстоянии 10 земных радиусов R_⊕; при слабом солнечном ветре это расстояние достигает 15—20 R_⊕, а в период магнитных возмущений на Земле магнитопауза может заходить за геостационарную орбиту (6,6 R_⊕)^[2]. Вытянутый хвост на ночной стороне имеет диаметр около 40 R_⊕ и длину более 900 R_⊕; начиная с расстояния примерно 8 R_⊕, он разделен на части плоским нейтральным слоем, в котором индукция поля близка к нулю^[2][4][7][8].

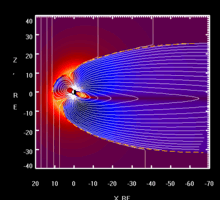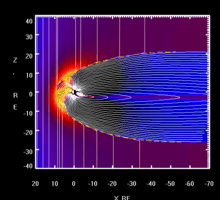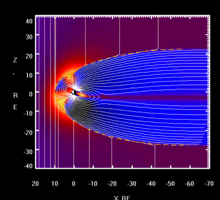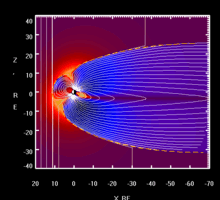Искажение магнитного поля Земли под действием солнечного ветра

Геомагнитное поле вследствие специфической конфигурации линий индукции создает для заряженных частиц — протонов и электронов — магнитную ловушку. Оно захватывает и удерживает огромное их количество, так что магнитосфера является своеобразным резервуаром заряженных частиц. Общая их масса, по различным оценкам, составляет от 1 кг до 10 кг. Они формируют так называемый радиационный пояс, охватывающий Землю со всех сторон, кроме приполярных областей. Его условно разделяют на два — внутренний и внешний. Нижняя граница внутреннего пояса находится на высоте около 500 км, его толщина — несколько тысяч километров. Внешний пояс находится на высоте 10—15 тыс. км. Частицы радиационного пояса под действием силы Лоренца совершают сложные периодические движения из Северного полушария в Южное и обратно, одновременно медленно перемещаясь вокруг Земли по азимуту. В зависимости от энергии они совершают полный оборот вокруг Земли за время от нескольких минут до суток^[7].

Магнитосфера не подпускает к земле потоки космических частиц^[8]. Однако в её хвосте, на больших расстояниях от Земли напряженность геомагнитного поля, а следовательно, и его защитные свойства, ослабляются, и некоторые частицы солнечной плазмы получают возможность попасть вовнутрь магнитосферы и магнитных ловушек радиационных поясов. Хвост таким образом служит местом формирования потоков высыпающихся частиц, вызывающих полярные сияния и авроральные токи^[2]. В полярных областях часть потока солнечной плазмы вторгается в верхние слои атмосферы из радиационного пояса Земли и, сталкиваясь с молекулами кислорода и азота, возбуждает их или ионизирует, а при обратном переходе в невозбужденное состояние атомы кислорода излучают фотоны с λ = 0,56 мкм и λ = 0,63 мкм, ионизированные же молекулы азота при рекомбинации высвечивают синие и фиолетовые полосы спектра. При этом наблюдаются полярные сияния, особенно динамичные и яркие во время магнитных бурь. Они происходят при возмущениях в магнитосфере, вызванных увеличением плотности и скорости солнечного ветра при усилении солнечной активности^[8][7].

Параметры поля[править | править код]

Наглядное представление о положении линий магнитной индукции поля Земли даёт магнитная стрелка, закреплённая таким образом, что может свободно вращаться и вокруг вертикальной, и вокруг горизонтальной оси (например, в кардановом подвесе), — в каждой точке вблизи поверхности Земли она устанавливается определённым образом вдоль этих линий.

Поскольку магнитные и географические полюса не совпадают, магнитная стрелка указывает направление с севера на юг только приблизительно. Вертикальную плоскость, в которой устанавливается магнитная стрелка, называют плоскостью магнитного меридиана данного места, а линию, по которой эта плоскость пересекается с поверхностью Земли, — магнитным меридианом^[6][8]. Таким образом, магнитные меридианы — это проекции силовых линий магнитного поля Земли на её поверхность, сходящиеся в северном и южном магнитных полюсах^[13]. Угол между направлениями магнитного и географического меридианов называют магнитным склонением. Оно может быть западным (часто обозначается знаком «−») или восточным (знак «+») в зависимости от того, к западу или востоку отклоняется северный полюс магнитной стрелки от вертикальной плоскости географического меридиана^[6][7][8].

Далее, линии магнитного поля Земли, вообще говоря, не параллельны её поверхности. Это означает, что магнитная индукция поля Земли не лежит в плоскости горизонта данного места, а образует с этой плоскостью некий угол — он называется магнитным наклонением^[6][8]. Оно близко к нулю лишь в точках магнитного экватора — окружности большого круга в плоскости, которая перпендикулярна к магнитной оси^[3].

Магнитное склонение и магнитное наклонение определяют направление магнитной индукции поля Земли в каждом конкретном месте. А численное значение этой величины можно найти, зная наклонение и одну из проекций вектора магнитной индукции B{\displaystyle \mathbf {B} } — на вертикальную или горизонтальную ось (последнее оказывается более удобным на практике). Таким образом, три этих параметра — магнитное склонение, наклонение и модуль вектора магнитной индукции B (либо вектора напряжённости магнитного поля H{\displaystyle \mathbf {H} }) — полностью характеризуют геомагнитное поле в данном месте. Их точное знание для максимально большого числа пунктов на Земле имеет чрезвычайно важное значение^[6][8]. Составляются специальные магнитные карты, на которых нанесены изогоны (линии одинакового склонения) и изоклины (линии одинакового наклонения), необходимые для ориентации с помощью компаса^[8].

В среднем интенсивность магнитного поля Земли колеблется от 25 до 65 мкТл (0,25—0,65 Гс) и сильно зависит от географического положения^[3]. Это соответствует средней напряжённости поля около 0,5 Э (40 А/м)^[2]. На магнитном экваторе её величина около 0,34 Э, у магнитных полюсов — около 0,66 Э. В некоторых районах (магнитных аномалий) напряжённость резко возрастает: в районе Курской магнитной аномалии она достигает 2 Э^[7].

Магнитный дипольный момент Земли на 2015 год составлял 7,72⋅10²⁵Гс·см³ (или 7,72⋅10²² А·м²), уменьшаясь в среднем за последние десятилетия на 0,007⋅10²⁵ Гс·см³ в год^[11].

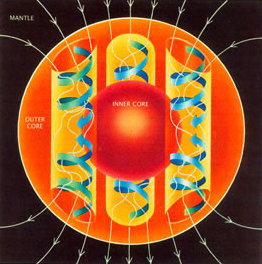Схема динамо-механизма: конвекционные потоки расплавленного металла во внешнем ядре формируют циркулирующие по замкнутому контуру токи, которые генерируют магнитное поле^[14]. Из-за вращения твёрдого ядра согласно теореме Тейлора-Праудмена^[en] скорость потоков постоянна вдоль вертикальной оси образующихся таким образом столбов Тейлора^[en], заключённых внутри цилиндра, ограничивающего внутреннее ядро, и подобных циклонам и антициклонам в атмосфере Земли^[15][16]. Первичные (по/против часовой стрелки) и вторичные (вертикальные сходящиеся/расходящиеся на экваторе) потоки вытягивают и поворачивают линии магнитного поля, превращая азимутальную компоненту в меридиональную и затем обратно^[17].

Впервые объяснить существование магнитных полей Земли и Солнца попытался Дж. Лармор в 1919 году^[18], предложив концепцию динамо, согласно которой поддержание магнитного поля небесного тела происходит под действием гидродинамического движения электропроводящей среды. Однако в 1934 году Т. Каулинг^[en][19] доказал теорему о невозможности поддержания осесимметричного магнитного поля посредством гидродинамического динамо-механизма. А поскольку большинство изучаемых небесных тел (и тем более Земля) считались аксиально-симметричными, на основании этого можно было сделать предположение, что их поле тоже будет аксиально-симметричным, и тогда его генерация по такому принципу будет невозможна согласно этой теореме^[20]. Даже Альберт Эйнштейн скептически относился к осуществимости такого динамо при условии невозможности существования простых (симметричных) решений. Лишь гораздо позже было показано, что не у всех уравнений с аксиальной симметрией, описывающих процесс генерации магнитного поля, решение будет аксиально-симметричным, и в 1950-х гг. несимметричные решения были найдены^[20][15].

С тех пор теория динамо успешно развивается, и на сегодняшний день общепринятым наиболее вероятным объяснением происхождения магнитного поля Земли и других планет является самовозбуждающийся динамо-механизм, основанный на генерации электрического тока в проводнике при его движении в магнитном поле, порождаемом и усиливаемом самими этими токами. Необходимые условия создаются в ядре Земли: в жидком внешнем ядре, состоящем в основном из железа при температуре порядка 4—6 тысяч кельвин, которое отлично проводит ток, создаются конвективные потоки, отводящие от твёрдого внутреннего ядра тепло (генерируемое благодаря распаду радиоактивных элементов либо освобождению скрытой теплоты при затвердевании вещества на границе между внутренним и внешним ядром по мере постепенного остывания планеты). Силы Кориолиса закручивают эти потоки в характерные спирали, образующие так называемые столбы Тейлора^[en]. Благодаря трению слоёв они приобретают электрический заряд, формируя контурные токи. Таким образом, создаётся система токов, циркулирующих по проводящему контуру в движущихся в (изначально присутствующем, пусть и очень слабом) магнитном поле проводниках, как в диске Фарадея. Она создает магнитное поле, которое при благоприятной геометрии течений усиливает начальное поле, а это, в свою очередь, усиливает ток, и процесс усиления продолжается до тех пор, пока растущие с увеличением тока потери на джоулево тепло не уравновесят притоки энергии, поступающей за счет гидродинамических движений^{[14][21][16][22]}. Высказывались предположения, что динамо может возбуждаться за счёт прецессии или приливных сил, то есть что источником энергии является вращение Земли, однако наиболее распространена и разработана гипотеза о том, что это всё же именно термохимическая конвекция^[17].

Математически этот процесс описывается магнитогидродинамическим уравнением индукции^{[en][16][17][23]}

∂B∂t=∇×(u×B)+η∇2B{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {\nabla } \times (\mathbf {u} \times \mathbf {B} )+\eta \mathbf {\nabla } ^{2}\mathbf {B} },

где u — скорость потока жидкости, B — магнитная индукция, η = 1/μσ — магнитная вязкость^[en] (коэффициент магнитной диффузии), σ — электропроводность жидкости, а μ — магнитная проницаемость, практически не отличающаяся при такой высокой температуре ядра от μ₀ — проницаемости вакуума. Первое слагаемое в правой части соответствует формированию магнитного поля, а второе — его подавлению. При u=0 (без динамо) решение этого уравнения — поле, полностью угасающее через 6⋅10⁴ лет^[23].

Однако для полного описания необходимо записать систему магнитогидродинамических уравнений. В приближении Буссинеска (в рамках которого пренебрегается т. н. вековым охлаждением и все физические характеристики жидкости полагаются постоянными, кроме силы Архимеда, при расчёте которой учитываются изменения плотности вследствие разности температур и — в общем случае — концентрации лёгких элементов) это^[16][17][23]:

ρ0(∂u∂t+u⋅∇u)=−∇P+ρ0ν∇2u+ρg¯−2ρ0Ω×u+J×B{\displaystyle \rho _{0}\left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \mathbf {u} \right)=-\nabla P+\rho _{0}\nu \mathbf {\nabla } ^{2}\mathbf {u} +\rho {\bar {\mathbf {g} }}-2\rho _{0}\mathbf {\Omega } \times \mathbf {u} +\mathbf {J} \times \mathbf {B} }.

Здесь ρ — плотность, ν — кинематическая вязкость, P=p−ρ02|Ω×r|2{\displaystyle P=p-{\frac {\rho _{0}}{2}}|\mathbf {\Omega } \times \mathbf {r} |^{2}} — «эффективное» давление с учётом центробежной силы (хотя в некоторых моделях она полагается пренебрежимо малой), g¯=g0rR0{\displaystyle {\bar {\mathbf {g} }}=g_{0}{\frac {\mathbf {r} }{R_{0}}}} — сила тяготения (R₀ — радиус внешнего ядра), Ω — угловая скорость вращения мантии, полагаемая равной скорости вращения внутреннего ядра, J=1μ∇×B{\displaystyle \mathbf {J} ={\frac {1}{\mu }}\nabla \times \mathbf {B} } — плотность тока согласно закону Ампера, индекс «0» всюду обозначает значения на границе внешнего ядра. Левая часть уравнения — производная от импульса на единицу объёма, то есть производная по времени от величины ρ₀V, увлекаемой движением жидкости; правая часть — сумма сил, вызывающих это изменение импульса: градиент давления^[en], вязкость, гравитация (сила Архимеда), вращение (сила Кориолиса) и магнитное поле (сила Лоренца)^[16].

Вращение Земли — один из важнейших факторов формирования геомагнитного поля, и его механизм схож с процессами в атмосфере Земли, приводящим к завихрению воздушных масс против часовой стрелки в северном полушарии и в обратном направлении в южном — циклонам и антициклонам. Аналогичные завихрения конвекционных потоков в ядре приводят к тому, что отдельные турбулентные конвекционные движения приобретают крупномасштабную (при усреднении по пульсациям скорости) зеркальную асимметрию и в совокупности приводят к генерации динамо в макроскопических масштабах благодаря электродвижущей силе, направленной уже вдоль, а не перпендикулярно среднему (которое определяется усреднением реального поля по его возможным статистическим реализациям) магнитному полю ⟨ε⟩=α⟨B⟩{\displaystyle \langle \mathbf {\varepsilon } \rangle =\alpha \langle \mathbf {B} \rangle }, где ε — ЭДС, а α — коэффициент пропорциональности, из-за которого этот механизм и получил название альфа-эффект^[22][24]. В общем случае α — тензор, однако зеркальная антисимметрия даёт псевдоскаляр, которого и требует по построению эта формула, так как ε — истинный вектор, а B — псевдовектор^[25]. Динамо, основанное исключительно на α-эффекте, называют α²-динамо, поскольку его действие выражается произведением двух членов, содержащих этот коэффициент^[23], — оно характеризуется практически стационарным полем, испытывающим небольшие кратковременные вариации (порядка сотен лет для Земли) и долговременные полные инверсии (порядка миллиона лет для Земли). Возможен также механизм с действием омега-эффекта (более существенного для Солнца, чем для Земли, однако необходимого для объяснения природы наблюдаемого дрейфа геомагнитных неоднородностей) — это измеряемое градиентом скорости дифференциальное вращение, которое из направленного к наблюдателю полоидального (вытянутого вдоль меридианов, B_S) магнитного поля создаёт скрытое в проводящем ядре планеты тороидальное (вытянутое вдоль параллелей, B_T) поле. Альфа-эффект замыкает цикл генерации — превращая тороидальное поле в полоидальное за счёт вихрей, характеризуемых отрицательной спиральностью (эта характеристика выражается соотношением u⋅∇×u{\displaystyle \mathbf {u} \cdot \mathbf {\nabla } \times \mathbf {u} } и непосредственно связана с величиной α) в Северном полушарии и положительной в Южном: восходящие и нисходящие потоки в конвекционных цилиндрах вытягивают и поворачивают B_T-линии в S-направлении^{[26][20][15][17]}. Такая схема обычно называется αω-эффектом, она даёт переменные поля, и при этом B_T>>B_S, тогда как для α²-механизма эти компоненты сравнимы (экспериментально на сегодняшний день удалось получить только грубую оценку |B_S|<|B_T|<100|B_S|). И если источником полоидального поля может быть только альфа-эффект, то тороидального — оба, причём если оба вносят существенный вклад, соответствующий механизм иногда обозначают α²ω. Большинство теоретических моделей магнитного динамо — типа α². В обоих случаях, как альфа, так и омега-эффектов, таким образом снимаются ограничения теоремы Каулинга^[16][23]. Однако существует ряд геометрий течений, для которых динамо также невозможно (например, чисто тороидальное поле скоростей^[23][27]), в то же время при определённых условиях оно возможно и при нулевой суммарной завихрённости ∇×u{\displaystyle \mathbf {\nabla } \times \mathbf {u} } и нулевой спиральности; возможны и другие эффекты, приводящие к возникновению ЭДС, параллельной магнитному полю^[25].

∂T∂t+u⋅∇T=κ∇2T+ϵ{\displaystyle {\frac {\partial T}{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } T=\kappa \mathbf {\nabla } ^{2}T+\epsilon },

где T — температура, κ = k/(ρc_p) — температуропроводность (коэффициент тепловой диффузии), k — теплопроводность, c_p — удельная теплоёмкость среды при постоянном давлении. Последнее слагаемое, ε, пропорционально выделению тепла, генерируемого теми или иными растворёнными в жидкости источниками (такими как радиоактивный распад), на единицу массы. В моделях, учитывающих перенос не только тепла, но и вещества, записывается соответствующее аналогичное уравнение относительно переменной ξ — массовой доли лёгких элементов (считается, что это сера и кислород) в составе ядра:

∂ξ∂t+u⋅∇ξ=κξ∇2ξ+ϵξ{\displaystyle {\frac {\partial \xi }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \xi =\kappa _{\xi }\mathbf {\nabla } ^{2}\xi +\epsilon _{\xi }},

где κ_ξ — коэффициент (молекулярной) диффузии. В большинстве моделей динамо, однако для простоты разность температур и концентраций лёгких элементов объединяются в одну отвечающую за плавучесть переменную.

∇⋅u=0{\displaystyle \mathbf {\nabla } \cdot \mathbf {u} =0}.

∇⋅B=0{\displaystyle \mathbf {\nabla } \cdot \mathbf {B} =0}.

ρ=ρ0[1−α(T−T0)]{\displaystyle \rho =\rho _{0}\left[1-\alpha (T-T_{0})\right]},

где α — коэффициент линейного теплового расширения (обозначение совпадает с коэффициентом пропорциональности в уравнении для альфа-эффекта). В общем случае, при учёте массопереноса, в квадратных скобках присутствует также слагаемое αξ(ξ−ξ0){\displaystyle \alpha _{\xi }(\xi -\xi _{0})}. Здесь α=−1ρ(∂ρ∂T)P,ξ{\displaystyle \alpha =-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial T}}\right)_{P,\xi }}, αξ=−1ρ(∂ρ∂ξ)P,T{\displaystyle \alpha _{\xi }=-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial \xi }}\right)_{P,T}}.

Естественно, необходимы также граничные условия для скорости потока, магнитного поля и разности температур, и многое зависит от того, как они ставятся в той или иной модели. Наибольший разброс имеет место в отношении потока тепла и вещества на границах между внутренним и внешним ядром, а также между внешним ядром и мантией, причём существенную роль играет неоднородность мантии и процессов в ней из-за тектоники плит^[16][17][28], которые, что немаловажно, протекают на порядки медленнее, нежели в ядре, что значительно осложняет комплексный анализ задачи.

Удобнее решать эту систему уравнений в безразмерном виде, вводя характерные величины длины, времени, скорости, магнитного поля и т. д.; тогда в них будут входить следующие безразмерные параметры^[16][17][29]:

Параметр	Формула	Определение	Значение в ядре Земли	Примечание
Входные параметры
Число Рэлея	Ra=g0αβ0R03νκ{\displaystyle Ra={\frac {g_{0}\alpha \beta _{0}R_{0}^{3}}{\nu \kappa }}}, где β0 — градиент температур на границе внешнего ядра (при r=R0). В зависимости от модели, встречаются и другие определения: g0αβ0DΩκ{\displaystyle {\frac {g_{0}\alpha \beta _{0}D}{\Omega \kappa }}} (D — толщина внешнего ядра), g0αQ02kκΩ{\displaystyle {\frac {g_{0}\alpha Q_{0}}{2k\kappa \Omega }}} (Q0=4πR02κβ0{\displaystyle Q_{0}=4\pi R_{0}^{2}\kappa \beta _{0}} — полный тепловой поток), g0αβ1R02ηΩ{\displaystyle {\frac {g_{0}\alpha \beta _{1}R_{0}^{2}}{\eta \Omega }}} (β1 — градиент температур на границе внутреннего и внешнего ядра) и т. п.[16]	соотношение интенсивности плавучести и вязкости, определяющее величину энергии, доступной системе для осуществления конвекции: конвекционный механизм теплопереноса будет преобладать над теплопроводностью, при Ra, большем некоторого критического значения	1024-1030, в зависимости от определения[16][23]
Число Экмана	E=ν2ΩR02{\displaystyle E={\frac {\nu }{2\Omega R_{0}^{2}}}}	соотношение вязкости (внутреннего трения) и силы Кориолиса: меньшее значение соответствует более быстрому вращению, и наоборот	10-15
Число Прандтля, а также (при учёте массопереноса) массовое число Прандтля	Pr=νκ{\displaystyle Pr={\frac {\nu }{\kappa }}}, Pc=νκξ{\displaystyle Pc={\frac {\nu }{\kappa _{\xi }}}}	соотношение характерных времён диффузии вязкой и тепловой, то есть кинематической вязкости и температуропроводности	~10-1	предположительно при преобладании турбулентной диффузии все числа Прандтля стремятся к 1, хотя вопрос о турбулентности в ядре изучен ещё недостаточно
Магнитное число Прандтля	Pm=νη{\displaystyle Pm={\frac {\nu }{\eta }}}	соотношение характерных времён диффузии магнитной и вязкой, то есть магнитных сил к силам внутреннего трения	10-6
Число Тейлора	Ta=(2ΩR02ν)2=1E2{\displaystyle Ta=\left({\frac {2\Omega R_{0}^{2}}{\nu }}\right)^{2}={\frac {1}{E^{2}}}}	соотношение между силой Кориолиса и силами вязкого трения
Модифицированное число Рэлея	RaM=αβ0g0R022Ωκ=E⋅Ra{\displaystyle Ra_{M}={\frac {\alpha \beta _{0}g_{0}R_{0}^{2}}{2\Omega \kappa }}=E\cdot Ra}	соотношение между силой Архимеда и силой Кориолиса
Магнитное число Экмана	EM=η2ΩR02=EPm{\displaystyle E_{M}={\frac {\eta }{2\Omega R_{0}^{2}}}={\frac {E}{Pm}}}	соотношение периода вращения и характерного времени магнитного взаимодействия
Соотношение коэффициентов диффузии магнитной и тепловой	q=κη=PmPr{\displaystyle q={\frac {\kappa }{\eta }}={\frac {Pm}{Pr}}}		1,7⋅10-5[23], 2⋅10-7[16]
Вычисляемые величины
Магнитное число Рейнольдса	Rm=u0R0η{\displaystyle Rm={\frac {u_{0}R_{0}}{\eta }}}, где u0 — характерная скорость потока. Локально в каждой точке величина определяется как Rm=|u×B||η

Действие магнитного поля на проводник с током

Е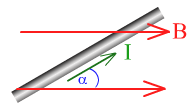сли поместить проводник с током в магнитное поле, то на него будет действовать сила, которая называется силой Ампера.

Сила Ампера — сила, с которой

магнитное поле действует на проводник с током

Сила Ампера вычисляется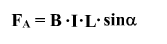

проводник перпендикулярен силовым линиям,

сила Ампера максимальна

проводник параллелен

силовым линиям, -сила Ампера равна нулю

Направление силы Ампера определяется по правилу левой руки.

Из опыта известно, что магнитное поле действует на проводник с током и на ток без проводника (пучки заряженных частиц). Следовательно,причина появления силы Ампера в том, что магнитное поле действует на движущиеся заряды.

Сила Ампера Сила Лоренца

Сила Лоренца – сила, с которой магнитное поле действует на движущийся заряд

модуль силы Лоренца вычисляется по формуле

Сила Лоренца направлена перпендикулярно скорости движения заряда и вектору магнитной индукции

Направление силы Лоренца вычисляется по правилу левой руки

для положительного заряда

для отрицательного заряда

37. Индукция магнитного поля. Магнитный поток. Явление электромагнитной

индукции и закон электромагнитной индукции Фарадея.

Индукция магнитного поля

Индукция магнитного поля – это силовая (векторная) характеристика магнитного поля.

Индукция В поля (магнитная индукция) – векторнаяхарактеристика магнитного поля.

Модуль вектора магнитной индукции равен отношению максимальной силы, действующей на проводник с током в магнитном поле, к силе этого тока и длине проводника

Равносильное определение

М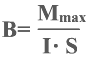одуль вектора магнитной индукции равенотношению максимального момента сил, действующего на контур с током в магнитном поле, к силе этого тока и площади контура

Единица измерения магнитной индукции:

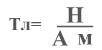[B] = 1 Тл (Тесла)

Физический смысл магнитной индукции:

Индукция магнитного поля численно равна максимальной силе, с которой данное поле действует на проводник длиной 1 метр с силой тока 1 Ампер.

Направление индукции магнитного поля –

от Южного к Северному полюсу свободно установившейся магнитной стрелки.

М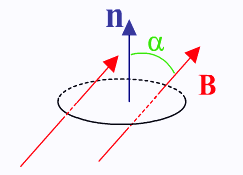агнитный поток

Нарисуем замкнутый контур, n– нормаль к его плоскости.

Поместим контур в магнитное поле с индукцией В.

Магнитный поток- это скалярная физическая величина, равная произведению модуля вектора индукции магнитного поля на площадь контура и на косинус угла между вектором индукции и нормалью к площади контура

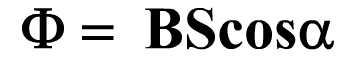
Единица измерения магнитного потока – Вебер

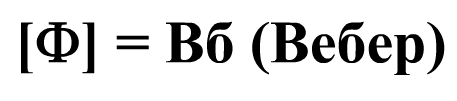
Вб = Тл*м²

Явление электромагнитной индукции

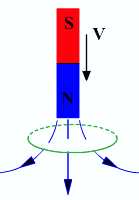
Явлениеэлектромагнитной индукциибыло открыто выдающимся английским физиком М. Фарадеем в 1831 г. Фарадей наблюдалвозникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.

Вопрос Фарадея:: если током можно намагнитить железо, то не может ли магнит вызвать появление тока?

Явление ЭМИ состоит в том,что при любом изменении магнитного потока, пронизывающего замкнутый контур, в контуре возникает ЭДС индукции. Если контур проводящий, то в нем будет протекать ток, который называется индукционным. Если контур из диэлектрика, то он поляризуется.

Сторонние силы действуют внутри источника тока и вызывают разделение зарядов, т. е. движение электронов от + к – источника. Имеют неэлектрическую природу.

ЭДС индукции возникает только в тот интервал времени, когда магнитный поток изменяется.

Изменение магнитного потока через контур:

.

Закон электромагнитной индукции (закон Фарадея)

ЭДС индукции

По закону ЭМИ изменение магнитного потока приводит к появлению ЭДС, которая называется ЭДС индукции.

О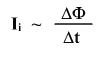пыт показывает, что сила токапропорциональна скорости изменения магнитного потока.

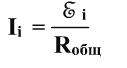По закону Ома для полной цепи сила тока равнаотношению ЭДС к полному сопротивлению цепи

следовательно, ЭДС индукции пропорциональна скорости изменения магнитного потока

Закон электромагнитной индукции (Фарадея):ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, взятой с обратным знаком. Знак означает правило Ленца.