Яндекс Андромеда – что изменилось в поиске и как теперь продвигать сайт

19 ноября Яндекс объявил о запуске нового поискового алгоритма – Андромеда. Традиция называть алгоритмы в честь городов ушла в прошлое. Символично, что последним был г. Королев, неофициальная космическая столица России. Дальше только космос. Поехали!

Напомню, что последнее глобальное официальное обновление алгоритма было еще в августе 2017. За это время специалисты Яндекса добавили в поиск более 1000 изменений и улучшений. Все они постепенно запускались, тестировались. Внедренные изменения можно разделить на три направления: новый алгоритм ранжирования, быстрые ответы, коллекции.

Новый алгоритм ранжирования сайтов в Яндекс Proxima

Логичное развитие предыдущего алгоритма Палех. Теперь качество сайта напрямую влияет на его место в выдаче. Если раньше Яндекс для оценки использовал определенные категории людей – ассесоров, специалистов Толоки и продвинутых пользователей, взаимодействующих с результатами поиска, то теперь для обучения алгоритма берутся «явные знания людей, которые могут с помощью сервисов и алгоритмов компании помогать другим людям совершать выбор или получать информацию в «Поиске».»

(из интервью руководителя Яндекс.Поиска Андрея Стыскина).

Еще один признак качественного сайта – лояльность. Яндекс учитывает постоянную аудиторию сайта, сколько людей возвращается после первого захода. Считает число переходов из внешних источников: социальных сетей, тематических форумов, справочников, Дзена. Используйте почтовую рассылку, публикуйте интересные статьи в ленте Дзен, держите пользователей в курсе об интересных акциях и предложениях через социальные сети. Чем популярнее сайт, тем он выше в органической выдаче.

Для таких сайтов теперь есть специальный значок:

Второй значок качественного сайта – Выбор пользователей:

Его может получить даже малопопулярный ресурс. Важно удержать костяк лояльной аудитории и работать над интересным контентом. Если после перехода пользователь надолго остался на сайте, а потом стал приходить вновь и вновь, такой сайт получает отметку «Выбор пользователей».

За прогрессом получения значков можно следить в Яндекс.Вебмастере, раздел – Показатели качества.

Третий признак качественного ресурса – отсутствие навязчивой рекламы. При переходе на сайт пользователь в первую очередь должен получить ответ на свой запрос, а не рекламный баннер во весь экран. Не следует использовать яркие, акцентирующие цвета, текст на странице должен быть легко читаем. Ничто не должно отвлекать внимание пользователя от просмотра контента.

Яндекс не запрещает размещать рекламу на сайте, просто не забывайте учитывать баланс полезного и навязчивого контента.

Еще один значок качественного сайта:

Доступен только для государственных сайтов, банков, внутренних сервисов Яндекс и официальных дилеров по данным портала Авто.ру.

Помогает защитить пользователя от мошенников, недобросовестных ресурсов и т.п. К примеру, если вам нужно получить загранпаспорт или подать заявление в ЗАГС, Яндекс подскажет ресурсы, где это можно сделать официально, без рисков отправить персональные данные шарлатанам.

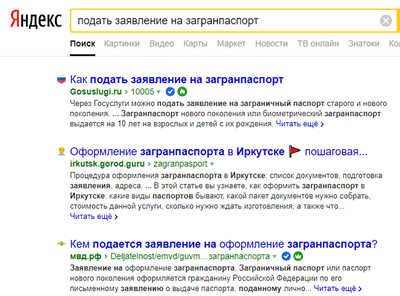
Качество сайта – новый, важный фактор ранжирования. Учитывайте это при составлении стратегии продвижения на следующий год.

Быстрые ответы

Одно из самых заметных обновлений – быстрые ответы в поисковой выдаче. Яндекс уже давно выдавал ответ на некоторые запросы прямо на станице поиска. Курс валюты, почтовый индекс, высота Эвереста и т.д. В большинстве случаев это были запросы фактического характера, без дополнительной ценности, когда нет разницы, на каком сайте получить подобную информацию.

Сейчас список таких запросов значительно расширился. Теперь это не только интересные факты, но и решение ежедневных бытовых задач.

Где поужинать любимой китайской едой?

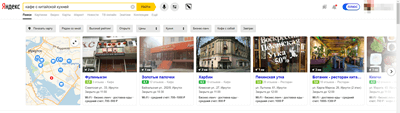
По запросу сразу же показывается карусель с подходящими ресторанами и кафе. Заведения можно отсортировать по нескольким параметрам.

Чтобы попасть в этот список организаций, необходимо полностью заполнить профиль компании в Яндекс.Справочнике. Указать время работы, добавить фотографии и дождаться отзывов от посетителей.

Еще пример быстрого ответа, рецепты:

«Колдунщики» Яндекс на базе микроразметки анализируют информацию на сайте, сравнивают между собой, и самые качественные показываются в быстрых ответах.

Быстрые ответы теперь подставляются и из сервиса Яндекс.Знатоки. 19 ноября он официально вышел из стадии бета-тестирования. Ответы дают как обычные пользователи, так и специально приглашенные эксперты – врачи, академики, учителя и студенты.

Компании также могут стать экспертами и отвечать на вопросы пользователей.

Никакой прямой рекламы продукта или услуги, только информационный ответ. Но в профиле можно указать подробное описание компании, оставить ссылку. Тут открываются большие возможности для крауд-маркетинга.

Яндекс.Коллекции

Теперь в один клик пользователи могут сохранять абсолютно все, что им понравилось в Сети. Книги, фильмы, рецепты, интерьеры и т.д. Все это попадает в сервис Яндекс.Коллекции.

Если коллекция общедоступна, она может попасть в выдачу по некоторым товарным запросам:

Сейчас сложно проследить четкую зависимость, как ранжируются коллекции в выдаче. На первых местах часто попадаются аккаунты с парой подписчиков и несколькими изображениями. Прямое вхождение ключевых слов важно, но оно не всегда играет решающую роль. К примеру, по запросу «красивые места Чечни» отображаются коллекции с названиями «Мечети Чечни», «Чечня», «Грозный», «Сердце Чечни» и т.д.

Алгоритм основывается на искусственном интеллекте и компьютерном зрении, он сам понимает, какие места относятся к Чечне, какие из них популярны и будут интересны пользователю. А дальше из публичных коллекций формируется ответ – наглядный пример работы нейросети Яндекс.

Андромеда – это новый подход Яндекса к обновлению поиска. Все фишки и изменения выкатываются постепенно, отследить, что именно влияет на проседание позиций сайта, становится все сложнее.

Качество сервиса в офлайне теперь напрямую влияет на позиции сайта в выдаче. Поведенческие факторы еще больше влияют на ранжирование, огромные баннеры во весь экран уходят в прошлое.

Главная задача Яндекс – дать пользователю быстрый и релевантный ответ из надежного источника. А задача вебмастеров сегодня – сделать сайт таким источником информации.

«Как работает алгоритм яндекса «Королёв»? Не документация в их блоге, а конкретно как сопоставляются вектора сравнения в нейронной сети? » – Яндекс.Знатоки

Как новый алгоритм Яндекса «Королёв» повлияет на продвижение

22 августа 2017 года «Яндекс» презентовал новый алгоритм ранжирования «Королёв», основанный на принципах нейронной сети. По словам компании, теперь поиск «Яндекса» будет точнее распознавать запросы пользователей не по прямым фразам, а по смыслу.

До этого в прошлом году «Яндекс» запустил алгоритм «Палех», который точнее понимал «длинный хвост» запросов, редко встречающихся в поиске из-за многословности или неточности.

Как новый алгоритм Яндекса «Королёв» повлияет на продвижение

Но оставалась проблема — как научить поиск определять ту самую релевантность «редкого» запроса и быстро выдавать нужные пользователю страницы.

Пример запроса из «длинного хвоста»
Раньше эту задачу решали с помощью метода машинного обучения «Матрикснет», который учитывал связь запроса с заголовком страницы. Но результаты поисковой выдачи были недостаточно релевантными. Поэтому в июле 2017 года Яндекс перешел на CatBoost — категориальный бустинг, на котором и работает «Королёв». Эта технология распознает данные из разнородных источников и учитывает категориальные признаки.

Разберем пример на яблоках. Бывают разные сорта: «Симиренко», «Гренни», «Антоновка», «Фуши». В этом случае сорт — это категория. Задача алгоритма — понять эту связь и предложить релевантные запросу страницы. Помимо этого, нужно учесть поведенческие сигналы — прочие запросы, по которым пользователи уже посещали сайт. Эти факторы и отличают новый метод от «Матрикснета».

Если целью «Матрикснета» было научиться понимать связи запросов с заголовками страниц, то CatBoost — со смыслом контента. Для этого и нужны категории. Со временем выдача запросов должна стать точнее и персонализированнее. Это и есть главная задача «Королёва», который, по сути, можно назвать «Палехом 2.0».

Если раньше для успешного продвижения нужно было создавать две одинаковые по смыслу страницы, но с разными заголовками, то в будущем достаточно будет одного качественного текста, чтобы покрывать разные многословные запросы.

Что теперь
Контент должен быть полезен, а не только напичкан точными вхождениями ключей. Еще нужно обратить внимание на синонимы поисковых фраз и слова, задающие тематику, чтобы сесть на «длинный хвост». Это уже не SEO-копирайтинг, а LSI-тексты. Употреблять фразы в них можно с разной частотностью, но они должны быть каким-то образом связаны с якорным запросом.

Слова, которые дополняют запрос «купить ноутбук»
Что же станет с коммерческими запросами? Ничего. Выдача по высокочастотным коммерческим запросам настолько «законсервирована», что интернет-магазины и в целом e-commerce не почувствует значимых изменений. В большей степени «Королёв» актуален для контентных проектов — блогов, журналов, СМИ, отраслевых порталов.

Компания Яндекс — Технологии — Маршрутизация

Десять-пятнадцать лет назад в бардачке каждого водителя лежал атлас дорог. Он и был главным помощником при планировании маршрута. Сейчас вместо атласа люди всё чаще открывают электронные карты или мобильные приложения, и умные алгоритмы сами строят для них наилучший маршрут. Яндекс помогает людям планировать поездки на сервисе maps.yandex.ru, в мобильных приложениях Навигатор и Яндекс.Карты. Технология построения маршрута везде одна и та же, различаются только интерфейсы.

Главные составляющие механизма маршрутизации — это дорожный граф и алгоритм, который рассчитывает путь.

Дорожный граф — это сетка дорог. Она состоит из множества фрагментов, которые состыкованы между собой. Например, дорожный граф Саратова (население — около 840 тысяч человек) состоит из 7592 фрагментов. Каждый из них несёт информацию о своём участке дороги: географические координаты, направление движения, средняя скорость, с которой машины обычно едут на этом участке, и другие параметры. Кроме того, каждый фрагмент содержит данные о том, как он стыкуется с соседними участками — есть ли в этом месте поворот направо или налево, можно ли там развернуться в обратную сторону или разрешается ехать только прямо.

Само собой, дорожный граф нельзя сделать раз и навсегда. Транспортная система города имеет обыкновение меняться. Появляются новые дороги и развязки, меняется направление движения. А там, где ещё недавно был поворот, может висеть «кирпич». Чтобы не отставать от жизни, Яндекс регулярно обновляет данные.

Во-первых, постоянно обрабатываются сообщения о неточностях в графе, которые пользователи присылают с помощью мобильных Яндекс.Карт, Навигатора и веб-сервиса Яндекс.Карты. С этими сообщениями работают эксперты Яндекса, которые используют также открытые источники информации о транспортной системе (например, сайты местных администраций).

Во-вторых, для определения неточностей на карте дорог существует специальная система. Она фиксирует все случаи, когда данные о движении машин, которые анонимно передают водители, не совпадают с имеющейся сеткой дорог. Если это не случайный нарушитель, который выехал на газон или развернулся в неположенном месте, возможно, на этом участке изменилась схема движения. Все такие случаи разбираются, и при необходимости в граф вносятся изменения.

Дорожный граф хранится на серверах Яндекса в нескольких экземплярах — если какой-то из серверов будет временно недоступен, маршрутизация все равно будет работать.

Маршрут рассчитывается по алгоритму Дейкстры. С его помощью система вычисляет самый быстрый вариант проезда — исходя из длины каждого отрезка графа и скорости движения на этом участке. Если пользователь строит маршрут проезда без учёта пробок, то алгоритм использует среднюю скорость движения на участке. А если пользователь хочет знать, как быстрее всего добраться до места с учётом ситуации на дороге, то алгоритм задействует данные о текущей ситуации на дороге.

Как это происходит, можно разобрать на примере. Представим, что нужно проложить маршрут из точки А в точку B. Алгоритм начинает методично перебирать все возможные варианты. Первым делом он прокладывает маршрут на один шаг (фрагмент графа) во все стороны от точки А. И затем вычисляет, сколько времени потребуется на преодоление этих участков (тут все просто — расстояние делится на скорость). Дальше он выбирает точку, до которой удалось бы добраться быстрее всего. Это точка С.

Затем алгоритм строит маршрут ещё на один шаг — во все стороны от точки С. И снова анализирует, в какую из точек можно было бы попасть быстрее всего. На этот раз это точка D. На следующем шаге алгоритм будет строить маршрут уже от неё.

Продолжая в том же духе, маршрутизатор находит вариант проезда, который оказывается самым коротким по времени.

Особая тема — дворы. Как известно, сквозной проезд через дворы запрещён. Кроме того, на петляния по ним зачастую уходит больше времени, чем на проезд по прямой. Чтобы сервис не строил маршруты через дворы, за них начисляются дополнительные минуты (они не влияют на время в пути, которое видит пользователь). Поэтому в большинстве случаев алгоритм выбирает другие варианты проезда — они занимают меньше времени. Однако если конечная точка маршрута находится во дворе, алгоритму в любом случае придётся туда «въехать».

Построение маршрута происходит очень быстро. Пока вы читаете эти несколько абзацев, сервис уже несколько раз успел бы оплести паутиной маршрутов всю Россию. Чтобы добиться такой скорости, всю карту автоматически поделили на множество областей, для каждой из которых можно посчитать оптимальные варианты её пересечения. Такой областью может быть, например, небольшой городок, через который проходит всего одна междугородняя трасса — въехать и выехать из города можно только по ней. Это значит, что Яндекс может заранее рассчитать оптимальный вариант проезда через этот город.

Если на пути пользователя лежат несколько таких областей, Яндекс просто складывает маршрут из уже готовых кусочков.

Всевозможные варианты проезда внутри каждой области и между ними Яндекс строит заранее — при каждом обновлении графа. Дальше, когда пользователь просит построить маршрут, сервис просто вытаскивает его из памяти. Правда, это срабатывает, только если человеку нужен маршрут без учёта пробок — заранее построенные маршруты рассчитаны на основе средней скорости движения, которая заложена в графе. Если же пользователь хочет построить маршрут с учетом ситуации на дороге и внутри области в данный момент есть пробки, Яндекс построит для него маршрут заново.

Искусственный интеллект в поиске. Как Яндекс научился применять нейронные сети, чтобы искать по смыслу, а не по словам

Сегодня мы анонсировали новый поисковый алгоритм «Палех». Он включает в себя все те улучшения, над которыми мы работали последнее время.

Например, поиск теперь впервые использует нейронные сети для того, чтобы находить документы не по словам, которые используются в запросе и в самом документе, а по смыслу запроса и заголовка.

Уже много десятилетий исследователи бьются над проблемой семантического поиска, в котором документы ранжируются, исходя из смыслового соответствия запросу. И теперь это становится реальностью.

В этом посте я постараюсь немного рассказать о том, как у нас это получилось и почему это не просто ещё один алгоритм машинного обучения, а важный шаг в будущее.

Искусственный интеллект или машинное обучение?

Почти все знают, что современные поисковые системы работают с помощью машинного обучения. Почему об использовании нейронных сетей для его задач надо говорить отдельно? И почему только сейчас, ведь хайп вокруг этой темы не стихает уже несколько лет? Попробую рассказать об истории вопроса.

Поиск в интернете — сложная система, которая появилась очень давно. Сначала это был просто поиск страничек, потом он превратился в решателя задач, и сейчас становится полноценным помощником. Чем больше интернет, и чем больше в нём людей, тем выше их требования, тем сложнее приходится становиться поиску.

Эпоха наивного поиска

Сначала был просто поиск слов — инвертированный индекс. Потом страниц стало слишком много, их стало нужно ранжировать. Начали учитываться разные усложнения — частота слов, tf-idf.

Эпоха ссылок

Потом страниц стало слишком много на любую тему, произошёл важный прорыв — начали учитывать ссылки, появился PageRank.

Эпоха машинного обучения

Интернет стал коммерчески важным, и появилось много жуликов, пытающихся обмануть простые алгоритмы, существовавшие в то время. Произошёл второй важный прорыв — поисковики начали использовать свои знания о поведении пользователей, чтобы понимать, какие страницы хорошие, а какие — нет.

Где-то на этом этапе человеческого разума перестало хватать на то, чтобы придумывать, как ранжировать документы. Произошёл следующий переход — поисковики стали активно использовать машинное обучение.

Один из лучших алгоритмов машинного обучения изобрели в Яндексе — Матрикснет. Можно сказать, что ранжированию помогает коллективный разум пользователей и «мудрость толпы». Информация о сайтах и поведении людей преобразуется во множество факторов, каждый из которых используется Матрикснетом для построения формулы ранжирования. Фактически, формулу ранжирования пишет машина (получалось около 300 мегабайт).

Но у «классического» машинного обучения есть предел: оно работает только там, где очень много данных. Небольшой пример. Миллионы пользователей вводят запрос [вконтакте], чтобы найти один и тот же сайт. В данном случае их поведение является настолько сильным сигналом, что поиск не заставляет людей смотреть на выдачу, а подсказывает адрес сразу при вводе запроса.

Но люди сложнее, и хотят от поиска всё больше. Сейчас уже до 40% всех запросов уникальны, то есть не повторяются хотя бы дважды в течение всего периода наблюдений. Это значит, что у поиска нет данных о поведении пользователей в достаточном количестве, и Матрикснет лишается ценных факторов. Такие запросы в Яндексе называют «длинным хвостом», поскольку все вместе они составляют существенную долю обращений к нашему поиску.

Эпоха искусственного интеллекта

И тут время рассказать о последнем прорыве: несколько лет назад компьютеры становятся достаточно быстрыми, а данных становится достаточно много, чтобы использовать нейронные сети. Основанные на них технологии ещё называют машинным интеллектом или искусственным интеллектом — потому что нейронные сети построены по образу нейронов в нашем мозге и пытаются эмулировать работу некоторых его частей.

Машинный интеллект гораздо лучше старых методов справляется с задачами, которые могут делать люди: например, распознаванием речи или образов на изображениях. Но как это поможет поиску?

Как правило, низкочастотные и уникальные запросы довольно сложны для поиска – найти хороший ответ по ним заметно труднее. Как это сделать? У нас нет подсказок от пользователей (какой документ лучше, а какой — хуже), поэтому для решения поисковой задачи нужно научиться лучше понимать смысловое соответствие между двумя текстами: запросом и документом.

Легко сказать

Строго говоря, искусственные нейросети – это один из методов машинного обучения. Совсем недавно им была посвящена лекция в рамках Малого ШАДа. Нейронные сети показывают впечатляющие результаты в области анализа естественной информации — звука и образов. Это происходит уже несколько лет. Но почему их до сих пор не так активно применяли в поиске?

Простой ответ — потому что говорить о смысле намного сложнее, чем об образе на картинке, или о том, как превратить звуки в расшифрованные слова. Тем не менее, в поиске смыслов искусственный интеллект действительно стал приходить из той области, где он уже давно король, — поиска по картинкам.

Несколько слов о том, как это работает в поиске по картинкам. Вы берёте изображение и с помощью нейронных сетей преобразуете его в вектор в N-мерном пространстве. Берете запрос (который может быть как в текстовом виде, так и в виде другой картинки) и делаете с ним то же самое. А потом сравниваете эти вектора. Чем ближе они друг к другу, тем больше картинка соответствует запросу.

Ок, если это работает в картинках, почему бы не применить эту же логику в web-поиске?

Дьявол в технологиях

Сформулируем задачу следующим образом. У нас на входе есть запрос пользователя и заголовок страницы. Нужно понять, насколько они соответствует друг другу по смыслу. Для этого необходимо представить текст запроса и текст заголовка в виде таких векторов, скалярное умножение которых было бы тем больше, чем релевантнее запросу документ с данным заголовком. Иначе говоря, мы хотим обучить нейронную сеть таким образом, чтобы для близких по смыслу текстов она генерировала похожие векторы, а для семантически несвязанных запросов и заголовков вектора должны различаться.

Сложность этой задачи заключается в подборе правильной архитектуры и метода обучения нейронной сети. Из научных публикаций известно довольно много подходов к решению проблемы. Вероятно, самым простым методом здесь является представление текстов в виде векторов с помощью алгоритма word2vec (к сожалению, практический опыт говорит о том, что для рассматриваемой задачи это довольно неудачное решение).

Дальше — о том, что мы пробовали, как добились успеха и как смогли обучить то, что получилось.

DSSM

В 2013 году исследователи из Microsoft Research описали свой подход, который получил название Deep Structured Semantic Model.

На вход модели подаются тексты запросов и заголовков. Для уменьшения размеров модели, над ними производится операция, которую авторы называют word hashing. К тексту добавляются маркеры начала и конца, после чего он разбивается на буквенные триграммы. Например, для запроса [палех] мы получим триграммы [па, але, лех, ех]. Поскольку количество разных триграмм ограничено, то мы можем представить текст запроса в виде вектора размером в несколько десятков тысяч элементов (размер нашего алфавита в 3 степени). Соответствующие триграммам запроса элементы вектора будут равны 1, остальные — 0. По сути, мы отмечаем таким образом вхождение триграмм из текста в словарь, состоящий из всех известных триграмм. Если сравнить такие вектора, то можно узнать только о наличии одинаковых триграмм в запросе и заголовке, что не представляет особого интереса. Поэтому теперь их надо преобразовать в другие вектора, которые уже будут иметь нужные нам свойства семантической близости.

После входного слоя, как и полагается в глубоких архитектурах, расположено несколько скрытых слоёв как для запроса, так и для заголовка. Последний слой размером в 128 элементов и служит вектором, который используется для сравнения. Выходом модели является результат скалярного умножения последних векторов заголовка и запроса (если быть совсем точным, то вычисляется косинус угла между векторами). Модель обучается таким образом, чтобы для положительны обучающих примеров выходное значение было большим, а для отрицательных — маленьким. Иначе говоря, сравнивая векторы последнего слоя, мы можем вычислить ошибку предсказания и модифицировать модель таким образом, чтобы ошибка уменьшилась.

Мы в Яндексе также активно исследуем модели на основе искусственных нейронных сетей, поэтому заинтересовались моделью DSSM. Дальше мы расскажем о своих экспериментах в этой области.

Теория и практика

Характерное свойство алгоритмов, описываемых в научной литературе, состоит в том, что они не всегда работают «из коробки». Дело в том, что «академический» исследователь и исследователь из индустрии находятся в существенно разных условиях. В качестве отправной точки (baseline), с которой автор научной публикации сравнивает своё решение, должен выступать какой-то общеизвестный алгоритм — так обеспечивается воспроизводимость результатов. Исследователи берут результаты ранее опубликованного подхода, и показывают, как их можно превзойти. Например, авторы оригинального DSSM сравнивают свою модель по метрике NDCG с алгоритмами BM25 и LSA. В случае же с прикладным исследователем, который занимается качеством поиска в реальной поисковой машине, отправной точкой служит не один конкретный алгоритм, а всё ранжирование в целом. Цель разработчика Яндекса состоит не в том, чтобы обогнать BM25, а в том, чтобы добиться улучшения на фоне всего множества ранее внедренных факторов и моделей. Таким образом, baseline для исследователя в Яндексе чрезвычайно высок, и многие алгоритмы, обладающие научной новизной и показывающие хорошие результаты при «академическом» подходе, оказываются бесполезны на практике, поскольку не позволяют реально улучшить качество поиска.

В случае с DSSM мы столкнулись с этой же проблемой. Как это часто бывает, в «боевых» условиях точная реализация модели из статьи показала довольно скромные результаты. Потребовался ряд существенных «доработок напильником», прежде чем мы смогли получить результаты, интересные с практической точки зрения. Здесь мы расскажем об основных модификациях оригинальной модели, которые позволили нам сделать её более мощной.

Большой входной слой

В оригинальной модели DSSM входной слой представляет собой множество буквенных триграмм. Его размер равен 30 000. У подхода на основе триграмм есть несколько преимуществ. Во-первых, их относительно мало, поэтому работа с ними не требует больших ресурсов. Во-вторых, их применение упрощает выявление опечаток и ошибок в словах. Однако, наши эксперименты показали, что представление текстов в виде «мешка» триграмм заметно снижает выразительную силу сети. Поэтому мы радикально увеличили размер входного слоя, включив в него, помимо буквенных триграмм, ещё около 2 миллионов слов и словосочетаний. Таким образом, мы представляем тексты запроса и заголовка в виде совместного «мешка» слов, словесных биграмм и буквенных триграмм.

Использование большого входного слоя приводит к увеличению размеров модели, длительности обучения и требует существенно больших вычислительных ресурсов.

Тяжело в обучении: как нейронная сеть боролась сама с собой и научилась на своих ошибках

Обучение исходного DSSM состоит в демонстрации сети большого количества положительных и отрицательных примеров. Эти примеры берутся из поисковой выдачи (судя по всему, для этого использовался поисковик Bing). Положительными примерами служат заголовки кликнутых документов выдачи, отрицательными — заголовки документов, по которым не было клика. У этого подхода есть определённые недостатки. Дело в том, что отсутствие клика далеко не всегда свидетельствует о том, что документ нерелевантен. Справедливо и обратное утверждение — наличие клика не гарантирует релевантности документа. По сути, обучаясь описанным в исходной статье образом, мы стремимся предсказывать аттрактивность заголовков при условии того, что они будут присутствовать в выдаче. Это, конечно, тоже неплохо, но имеет достаточно косвенное отношение к нашей главной цели — научиться понимать семантическую близость.

Во время своих экспериментов мы обнаружили, что результат можно заметно улучшить, если использовать другую стратегию выбора отрицательных примеров. Для достижения нашей цели хорошими отрицательными примерами являются такие документы, которые гарантированно нерелевантны запросу, но при этом помогают нейронной сети лучше понимать смыслы слов. Откуда их взять?

Первая попытка

Сначала в качестве отрицательного примера просто возьмём заголовок случайного документа. Например, для запроса [палехская роспись] случайным заголовком может быть «Правила дорожного движения 2016 РФ». Разумеется, полностью исключить то, что случайно выбранный из миллиардов документ будет релевантен запросу, нельзя, но вероятность этого настолько мала, что ей можно пренебречь. Таким образом мы можем очень легко получать большое количество отрицательных примеров. Казалось бы, теперь мы можем научить нашу сеть именно тому, чему хочется — отличать хорошие документы, которые интересуют пользователей, от документов, не имеющих к запросу никакого отношения. К сожалению, обученная на таких примерах модель оказалась довольно слабой. Нейронная сеть – штука умная, и всегда найдет способ упростить себе работу. В данном случае, она просто начала выискивать одинаковые слова в запросах и заголовках: есть — хорошая пара, нет — плохая. Но это мы и сами умеем делать. Для нас важно, чтобы сеть научилась различать неочевидные закономерности.

Ещё одна попытка

Следующий эксперимент состоял в том, чтобы добавлять в заголовки отрицательных примеров слова из запроса. Например, для запроса [палехская роспись] случайный заголовок выглядел как [Правила дорожного движения 2016 РФ роспись]. Нейронной сети пришлось чуть сложнее, но, тем не менее, она довольно быстро научилась хорошо отличать естественные пары от составленных вручную. Стало понятно, что такими методами мы успеха не добьемся.

Успех

Многие очевидные решения становятся очевидны только после их обнаружения. Так получилось и на этот раз: спустя некоторое время обнаружилось, что лучший способ генерации отрицательных примеров — это заставить сеть «воевать» против самой себя, учиться на собственных ошибках. Среди сотен случайных заголовков мы выбирали такой, который текущая нейросеть считала наилучшим. Но, так как этот заголовок всё равно случайный, с высокой вероятностью он не соответствует запросу. И именно такие заголовки мы стали использовать в качестве отрицательных примеров. Другими словами, можно показать сети лучшие из случайных заголовков, обучить её, найти новые лучшие случайные заголовки, снова показать сети и так далее. Раз за разом повторяя данную процедуру, мы видели, как заметно улучшается качество модели, и всё чаще лучшие из случайных пар становились похожи на настоящие положительные примеры. Проблема была решена.

Подобная схема обучения в научной литературе обычно называется hard negative mining. Также нельзя не отметить, что схожие по идее решения получили широкое распространение в научном сообществе для генерации реалистично выглядящих изображений, подобный класс моделей получил название Generative Adversarial Networks.

Разные цели

В качестве положительных примеров исследователи из Microsoft Research использовались клики по документам. Однако, как уже было сказано, это достаточно ненадежный сигнал о смысловом соответствии заголовка запросу. В конце концов, наша задача состоит не в том, чтобы поднять в поисковой выдаче самые посещаемые сайты, а в том, чтобы найти действительно полезную информацию. Поэтому мы пробовали в качестве цели обучения использовать другие характеристики поведения пользователя. Например, одна из моделей предсказывала, останется ли пользователь на сайте или уйдет. Другая – насколько долго он задержится на сайте. Как оказалось, можно заметно улучшить результаты, если оптимизировать такую целевую метрику, которая свидетельствует о том, что пользователь нашёл то, что ему было нужно.

Профит

Ок, что это нам дает на практике? Давайте сравним поведение нашей нейронной модели и простого текстового фактора, основанного на соответствии слов запроса и текста — BM25. Он пришёл к нам из тех времён, когда ранжирование было простым, и сейчас его удобно использовать за базовый уровень.

В качестве примера возьмем запрос [келлская книга] и посмотрим, какое значение принимают факторы на разных заголовках. Для контроля добавим в список заголовков явно нерелевантный результат.

Заголовок страницы	BM25	Нейронная модель
келлская книга википедия	0.91	0.92
ученые исследуют келлскую книгу вокруг света	0.88	0.85
book of kells wikipedia	0	0.81
ирландские иллюстрированные евангелия vii viii вв	0	0.58
икеа гипермаркеты товаров для дома и офиса ikea	0	0.09

Все факторы в Яндексе нормируются в интервал [0;1]. Вполне ожидаемо, что BM25 имеет высокие значения для заголовков, которые содержат слова запроса. И вполне предсказуемо, что этот фактор получает нулевое значение на заголовках, не имеющих общих слов с запросом. Теперь обратите внимание на то, как ведет себя нейронная модель. Она одинаково хорошо распознаёт связь запроса как с русскоязычным заголовком релевантной страницы из Википедии, так и с заголовком статьи на английском языке! Кроме того, кажется, что модель «увидела» связь запроса с заголовком, в котором не упоминается келлская книга, но есть близкое по смыслу словосочетание («ирландские евангелия»). Значение же модели для нерелевантного заголовка существенно ниже.

Теперь давайте посмотрим, как будут себя вести наши факторы, если мы переформулируем запрос, не меняя его смысла: [евангелие из келлса].

Заголовок страницы	BM25	Нейронная модель
келлская книга википедия	0	0.85
ученые исследуют келлскую книгу вокруг света	0	0.78
book of kells wikipedia	0	0.71
ирландские иллюстрированные евангелия vii viii вв	0.33	0.84
икеа гипермаркеты товаров для дома и офиса ikea	0	0.10

Для BM25 переформулировка запроса превратилась в настоящую катастрофу — фактор стал нулевым на релевантных заголовках. А наша модель демонстрирует отличную устойчивость к переформулировке: релевантные заголовки по-прежнему имеют высокое значение фактора, а нерелевантный заголовок — низкое. Кажется, что именно такое поведение мы и ожидали от штуки, которая претендует на способность «понимать» семантику текста.

Ещё пример. Запрос [рассказ в котором раздавили бабочку].

Заголовок страницы	BM25	Нейронная модель
фильм в котором раздавили бабочку	0.79	0.82
и грянул гром википедия	0	0.43
брэдбери рэй википедия	0	0.27
машина времени роман википедия	0	0.24
домашнее малиновое варенье рецепт заготовки на зиму	0	0.06

Как видим, нейронная модель оказалась способна высоко оценить заголовок с правильным ответом, несмотря на полное отсутствие общих слов с запросом. Более того, хорошо видно, что заголовки, не отвечающие на запрос, но всё же связанные с ним по смыслу, получают достаточно высокое значение фактора. Как будто наша модель «прочитала» рассказ Брэдбери и «знает», что это именно о нём идёт речь в запросе!

А что дальше?

Мы находимся в самом начале большого и очень интересного пути. Судя по всему, нейронные сети имеют отличный потенциал для улучшения ранжирования. Уже понятны основные направления, которые нуждаются в активном развитии.

Например, очевидно, что заголовок содержит неполную информацию о документе, и хорошо бы научиться строить модель по полному тексту (как оказалось, это не совсем тривиальная задача). Далее, можно представить себе модели, имеющие существенно более сложную архитектуру, нежели DSSM — есть основания предполагать, что таким образом мы сможем лучше обрабатывать некоторые конструкции естественных языков. Свою долгосрочную цель мы видим в создании моделей, способных «понимать» семантическое соответствие запросов и документов на уровне, сравнимом с уровнем человека. На пути к этой цели будет много сложностей — тем интереснее будет его пройти. Мы обещаем рассказывать о своей работе в этой области. Cледите за следующими публикациями.

Результаты и разбор задач финала Яндекс.Алгоритма 2016 / Яндекс corporate blog / Habr

29 июля в Минске прошёл финальный раунд чемпионата по программированию Яндекс.Алгоритм. Победителем стал Егор EgorK Куликов — выпускник мехмата МГУ и бывший сотрудник Яндекса. Второе место — у Николы Йокича из Швейцарской высшей технической школы Цюриха. В составе команды школы он был финалистом ACM ICPC. Третье место занял Макото Соэдзима, выпускник Университета Токио. Геннадий Короткевич, победитель двух предыдущих Алгоритмов, занял шестое место.

Как и в прошлые годы, мы публикуем подробный разбор финальных задач. 31 июля мы впервые провели зеркало Алгоритма. Поэтому, чтобы не испортить его участникам удовольствие, не стали публиковать ответы сразу же после финала, как мы это обычно делаем.

В этом году мы получили на четверть больше заявок на участие в Алгоритме, чем год назад, — 4578. Среди участников пока немного девушек — 372. В списке зарегистрировавшихся есть представители 70 стран; больше всего соревнующихся — из России, Индии, Украины, Беларуси, Казахстана, США и Китая. В финале приняли участие 25 человек.

Задачи для Яндекс.Алгоритма составляют сотрудники Яндекса и приглашённые эксперты, среди которых — финалисты и призёры ACM ICPC. По условиям состязания, участники могут использовать разные языки программирования. Статистика Яндекс.Алгоритма показывает, что самый популярный язык — С++; его выбрали более двух тысяч человек. Второе место поделили Python и Java.

Задача A. Место проведения финала

Авторы задачи: Алексей Толстиков, Роман Удовиченко

Имя входного файла:	Имя выходного файла:	Ограничение по времени:	Ограничение по памяти:
стандартный ввод	стандартный вывод	3 секунды	512 мегабайт

В этом году финал Яндекс.Алгоритма проходит в Национальной библиотеке Беларуси. Хочется отметить, что здание библиотеки имеет весьма необычную форму — ромбокубоктаэдр.

Ромбокубооктаэдр это полуправильный многогранник, гранями которого являются 18 квадратов и 8 треугольников. Всего у ромбокубооктаэдра 24 вершины и 48 ребер. Изображение ромбокубооктаэдра представлено ниже:

В этой задаче вам требуется определить количество способов покрасить грани ромбокубоктаэдра таким образом, чтобы никакие две грани, имеющие общее ребро, не были покрашены в один цвет. Всего в вашем распоряжении имеется k цветов.

Так как ответ может достаточно большим, вычислите его по модулю 10⁹ + 7.

Формат входных данных

В единственной строке входных данных записано одно целое число k (1 ⩽ k ⩽ 50), количество цветов в вашем распоряжении.

Формат выходных данных

В единственной строке выведите ответ на задачу.

Примеры

стандартный ввод	стандартный вывод
1	0
3	356928

Замечание

Одним из вариантов корректной раскраски для k = 3 будет покрасить все треугольные грани в первый цвет (8 граней), все квадратные грани, смежные по ребру с одной из треугольных граней, во второй цвет (12 граней), и все оставшиеся квадратные грани в третий цвет (6 граней).

Разбор задачи A

Рассмотрим новый граф, вершинами которого являются грани ромбокубооктаэдра, а рёбрами соединены те вершины, которые соответствуют граням, смежным по стороне (так называемый двойственный граф многогранника). Наша задача принимает следующий вид: нужно посчитать количество правильных раскрасок получившегося графа в k цветов, где правильная раскраска — это такая раскраска, что соседние вершины окрашены в разные цвета.

Заметим, что наш граф является двудольным: его вершины можно разбить на две группы, состоящие из 12 вершин и из 14 вершин, таким образом, что рёбра соединяют только вершины разных групп. На самом деле, в условии даже указано, как именно устроено это разбиение: первую долю разбиения образуют вершины, которые в пояснении предлагается покрасить во второй цвет, а вторую долю — все остальные.

Будем сначала красить первую долю, а только потом вторую. Заметим, что при фиксированной раскраске первой доли посчитать количество способов, которыми можно докрасить вторую долю, не составляет труда: каждую вершину второй доли мы красим в отдельности, а значит, общее число способов есть произведение по всем вершинам второй доли v величины k − adj(v), где adj(v) — количество различных цветов среди вершин, смежных v.

Теперь надо каким-то образом перебрать раскраску первой доли. Если явно перебирать цвет для каждой вершины, это потребует порядка 50¹² ≈ 2,4 · 10²⁰ операций, что не уложится ни в какие разумные временные рамки. Будем перебирать не сами цвета вершин, а только их разбиение на одинаковые/разные цветовые группы. А именно — для каждой очередной вершины в ходе перебора будем принимать решение, отнести ли её к одному из уже имеющихся цветов вершин, либо завести ли для неё новый. Таких «сжатых» раскрасок уже не так много, всего 4 213 597 штук. Очевидно, информации, содержащейся в сжатой раскраске первой доли, достаточно для того, чтобы понять, сколькими способами можно докрасить вторую долю, надо только не забыть умножить это число на количество способов превратить данную сжатую раскраску в полноценную раскраску (оно равняется A(k, c) = k(k − 1)(k − 2)…(k − c + 1), где c — количество использованных в сжатой раскраске цветов).

Если написанное решение не укладывается в ограничение по времени, но работает не сильно долго на одном тесте, то можно схитрить и воспользоваться тем, что ограничение на k не очень большое, посчитав на локальном компьютере все 50 ответов на тесты и просто вбив в программу.

Альтернативное решение может перебирать раскраску на поясе из 8 средних квадратов, а дальше считать количество способов докрасить одну из половин и возводить его в квадрат, так как верхняя и нижняя половина ромбокубооктаэдра красятся независимо друг от друга.

---

Задача B. Преобразование последовательности

Авторы задачи: Максим Ахмедов, Глеб Евстропов

Имя входного файла:	Имя выходного файла:	Ограничение по времени:	Ограничение по памяти:
стандартный ввод	стандартный вывод	1 секунда	512 мегабайт

Вам дана последовательность a₁, a₂,…, a_n, исходно состоящая из n нулей. За один ход вы можете выбрать любой её подотрезок a_l, a_l+1,…,a_r, а также произвольное целое число x и преобразовать последовательность этот подотрезок, заменив a_l+k на a_l+k + (−1)^k · x для всех целых 0 ⩽ k ⩽ r − l.

Требуется преобразовать исходную нулевую последовательность в данную последовательность b₁, b₂,…, b_n за минимальное число ходов. Имеется важное ограничение на последовательность b_i: гарантируется, что все её элементы принадлежат множеству {−1, 0, 1}.

Формат входных данных

В первой строке входных данных находится единственное целое число n (1 ⩽ n ⩽ 10⁵). Вторая строка содержит n целых чисел b₁, b₂,…, b_n (−1 ⩽ b_i ⩽ 1).

Формат выходных данных

Выведите минимальное число ходов, необходимое для того, чтобы преобразовать исходную последовательность в требуемую.

Примеры

стандартный ввод	стандартный вывод
2 -1 1	1
5 1 -1 1 1 0	2

Замечание

В первом тесте из условия можно получить требуемую последовательность за один ход, в котором x = −1, l = 1 и r = 2.

Во втором тесте из условия можно действовать следующим образом:
0 0 0 0 0 → 2 -2 2 0 0 → 1 -1 1 1 0

Разбор задачи B

Будем постепенно разбираться в конструкции. Во-первых, инвертируем знаки у всех чисел, стоящих на чётных позициях. Теперь операция, указанная в условии, будет действовать проще: нам разрешается выбрать любой подотрезок и прибавить ко всем числам на нём одно и то же число t.

Раз мы имеем дело с операциями вида «прибавить на подотрезке одно и то же число», то полезно перейти к последовательности, состоящей из разностей соседних элементов: перейдём от a₁, a₂,…,a_n к последовательности b₀ = a₁, b₁ = a₂ − a₁,…, b_i = a_i+1 − a_i,…, b_n = −a_n. В этой последовательности элементов на один больше, и она удовлетворяет специальному условию, что b₀ + b₁ +… + b_n = 0.

Тогда прибавление константы x на отрезке [l, r] исходной последовательности эквивалентно замене b_l−1 → b_l−1 + x и b_r → b_r − x.

В последовательности a_i встречались целые числа от −1 до 1, поэтому в последовательности b_i будут встречаться целые числа от −2 до 2. За один ход, как мы уже выяснили, мы можем к одному из чисел прибавить x, а из другого вычесть x, и мы хотим добиться, чтобы в последовательности были одни нули.

Назовём «весом» операции прибавления x и −x к двум элементам последовательности величину |x|.

Докажем вспомогательный факт: если число b_i больше (меньше) нуля, то не выгодно применять операции, в которых число b_i увеличивается. Формально говоря, если есть оптимальная (т. е. кратчайшая) последовательность операций, в которой какое-то b_i в какой-то момент увеличивается, то можно предъявить последовательность операций, в которой ни одно b_i никогда не увеличивается, и которая имеет ту же длину.

Действительно, пусть к b_i применялись две операции, скажем, 1) b_i → b_i + x, b_j → b_j − x и 2) b_i + x → b_i + x − y, b_k → b_k +y, и, для определённости, где x,y > 0 и, для определённости, x ⩽ y.

Давайте заменим эти две операции на две других: 1) b_i → b_i − (y − x) = b_i + x − y, b_k → b_k + y − x и b_j → b_j − x, b_k + y − x → b_k + y − x + x = b_k + y. Это две эквивалентные операции, они приводят к тем же результатам, но можно увидеть, что суммарный вес двух новых операций уменьшился: |y − x| + |x| = y − x + x = y < x + y = |x| + |y|.

Повторяя такие замены, пока возможно, мы рано или поздно остановимся (потому что суммарный вес операций не может неограниченно убывать, так как он всегда целый и неотрицательный), а значит, можно найти последовательность операций той же длины, в которой любой положительный элемент всегда только уменьшается. Аналогично можно добиться того, что любой положительный элемент будет только увеличиваться.

Это позволяет описать все доступные нам операции. Мы можем либо избавиться от −2 и 2 за один ход, либо избавиться от −1 и 1 за один ход, либо избавиться от −2, 1, 1 за два хода, либо избавиться от 2, −1, −1 за два хода.

Понятно, что суммарный вес всех операций, которые мы произведём, есть сумма всех положительных чисел среди b_i (которая противоположна по знаку сумме всех отрицательных чисел). У нас теперь бывают операции веса 1 и веса 2, и понятно, что чтобы минимизировать общее число операций, надо сделать как можно больше операций веса 2. Это приводит нас к жадному алгоритму, а именно — сокращать двойки с минус двойками, пока можем, а когда не больше не можем, сокращать единички и минус единички с чем получится.

Таким образом, ответ это сумма всех положительных b_i минус минимум из количества двоек и количества минус двоек.

---

Задача C. Игра в шляпу

Автор задачи: Глеб Евстропов

Имя входного файла:	Имя выходного файла:	Ограничение по времени:	Ограничение по памяти:
стандартный ввод	стандартный вывод	1 секунда	512 мегабайт

Шляпа это популярная в русскоговорящих странах игра, рассчитанная на большую дружную компанию. Участники разбиваются на команды по двое и садятся в круг таким образом, чтобы каждый сидел строго напротив своего партнёра. Играющие пишут множество слов на маленьких бумажках, кладут их в шляпу, после чего каждый из игроков по очереди пытается объяснить своему партнёру выпадавшее ему слово, не называя его при этом явно.

Рассмотрим следующую задачу. За круглым столом сидят 2n людей. Они хотят поиграть в шляпу, и они уже разбились некоторым образом на команды по двое. Теперь они хотят пересесть таким образом, чтобы каждый человек сидел напротив своего партнёра. Для этого они могут несколько раз произвести следующую операцию: они выбирают двух людей из сидящих за столом и просят их поменяться местами.

Вам дано начальное расположение людей за столом. Определите, какое минимальное количество операций описанного вида надо произвести, чтобы каждый человек сидел напротив своего партнёра.

Формат входных данных

В первой строке входных данных находится целое число n (1 ⩽ n ⩽ 10⁵), означающее, что за столом сидят 2n человек.

Во второй строке находится последовательность из 2n целых чисел. Каждое целое число от 1 до n встречается в этой последовательности ровно два раза. Эта последовательность описывает разбиение людей, сидящих вокруг стола, на команды, если мы будем их выписывать в порядке обхода по часовой стрелке.

Формат выходных данных

Выведите минимальное число операций, которые надо произвести, чтобы каждый человек оказался напротив своего партнёра.

Примеры

стандартный ввод	стандартный вывод
3 2 1 3 2 1 3	0
4 2 1 4 2 3 1 3 4	2

Замечание

В первом тесте из условия начальная рассадка уже подходит для игры в шляпу.

Во втором тесте из условия один из оптимальных способов будет сначала поменять местами людей, сидящих на первой и седьмой позициях, а потом поменять местами людей, сидящих на седьмой и восьмой позициях, что приведёт нас к корректной рассадке: 3 1 4 2 3 1 4 2.

Разбор задачи C

Рассмотрим следующий граф: его вершинами будут 2n позиций за столом, а рёбрами будут соединены, во-первых, вершины, соответствующие диаметрально противоположным позициям, а во-вторых — вершины, соответствующие позициям, на которых сидят люди из одной команды. В частности, если люди из одной команды уже сидят друг напротив друга, то между вершинами, соответствующими их позициям, будет проведено два ребра.

Получившийся граф обладает тем свойством, что в нём из каждой вершины ведёт ровно два ребра (одно — диаметр, а второе — в вершину, в которой сидит человек из той же команды). Такой граф всегда представляет из себя объединение из какого-то количества циклов.

Мы стремимся достигнуть ситуации, когда каждый цикл состоит ровно из двух диаметрально противоположных вершин, то есть когда всего имеется ровно n циклов длины 2.

Поймём, как меняется наш граф под воздействием доступной нам операции. Пусть поменяли местами двух людей не из одной команды (иначе это бессмысленная операция), скажем, человека из вершины a с человеком из вершины b. Пусть партнёр человека a сидит в вершине a′, а партнёр человека b сидит в вершине b′. Тогда из графа пропадут два ребра aa′ и bb′ и образуются два новых ребра ba′ и ab′ (то есть новые рёбра будут идти крест-накрест между концами старых). Легко видеть, что такая операция может либо один цикл разъединить на два, либо не изменить количество циклов, либо склеить два цикла. Значит, ответ никак не меньше, чем n − c, где c — исходное количество циклов. С другой стороны, всегда можно добиться требуемого ровно за столько ходов: достаточно на каждом шаге брать пару сокомандников, которые сидят не друг напротив друга, и просто пересаживать одного из них так, чтобы он сел напротив своего партнёра. Эта операция строго увеличивает количество циклов на один.

Таким образом, ответ есть n − c, где c — количество циклов, или, что то же самое, компонент связности в указанном графе. Эту задачу можно решить и просто явно моделируя процесс рассаживания людей по парам, и это корректно по тем же причинам, которые описаны выше.

---

Задача D. Кучефицируй меня полностью

Автор задачи: Максим Ахмедов

Имя входного файла:	Имя выходного файла:	Ограничение по времени:	Ограничение по памяти:
стандартный ввод	стандартный вывод	2 секунды	512 мегабайт

Вы — простой паренёк, который хочет лишь одного: чтобы ему на день рождения подарили двоичную максимальную кучу, потому что у всех ваших друзей уже такая есть! Наконец, вы пошли с родителями в магазин, но, к сожалению, там закончились все двоичные кучи, и всё, что осталось — это старое полное двоичное дерево. Оно состоит из n = 2^h − 1 вершин, в которых записаны некоторые значения, не обязательно удовлетворяющие главному свойству максимальной кучи. К счастью, Старый Джо согласился помочь вам превратить это дерево в двоичную кучу за определённую плату.

Полное двоичное дерево высоты h это корневое дерево, состоящее из n = 2^h − 1 вершин, пронумерованных от 1 до n, такое, что для любого 1 ⩽ v ⩽ 2^h-1 − 1 вершина v является предком для вершин 2v и 2v + 1.

Двоичная максимальная куча высоты h это полное бинарное дерево высоты h, у которого в вершинах находятся значения h₁, h₂,…, h_n, при этом значение в любой вершине не меньше, чем значение в её детях (если у неё есть дети).

Вам дано полное бинарное дерево высоты h, в вершинах которого находятся значения a₁,a₂,…,a_n. Также, с каждой вершиной связана стоимость c_v, означающая, что Старый Джо может как увеличить, так и уменьшить значение в вершине v на произвольную величину x > 0 за стоимость в c_vx. Вы можете менять значения в произвольном количестве вершин.

Определите минимальную стоимость преобразования данного полного бинарного дерева в максимальную кучу.

Формат входных данных

В первой строке ввода находится единственное целое число n (1 ⩽ n ⩽ 2¹⁸−1), количество вершин в полном бинарном дереве, которое вам досталось. Гарантируется, что n = 2^h − 1 для некоторого целого h.

Во второй строке ввода находятся n целых чисел a₁, a₂,…, a_n (0 ⩽ a_i ⩽ 10⁶), текущие значения вершин дерева.

В третьей строке находятся n целых чисел c₁, c₂,…, c_n (0 ⩽ c_i ⩽ 10⁶), стоимости изменения значений в вершинах дерева.

Формат выходных данных

Выведите минимальную стоимость преобразования данного полного бинарного дерева в максимальную кучу.

Пример

стандартный ввод	стандартный вывод
7 4 5 3 1 2 6 6 4 7 8 0 10 2 3	19

Замечание

В тесте из условия оптимальным способом будет увеличить значение в вершине 1 на 2 ценой в 4 · 2 = 8 и уменьшить значения в вершинах 6 и 7 на 3 ценой в 2 · 3 = 6 и 3 · 3 = 9 соответственно. Таким образом, общая стоимость будет равна 8 + 6 + 9 = 23.

Разбор задачи D

Введём обозначения. Пусть L_v(x) — это минимальная цена, которую надо заплатить, чтобы поддерево вершины v стало корректной кучей, а в самой вершине v стояло число, не превосходящее x. Пусть S_v(x) — это величина, которая определяется абсолютно аналогично, только в самой вершине v должно стоять строго число x. Тогда ответ на задачу равняется значению минимума функции S_v(x).

Для листовых вершин v по условию имеем, что S_v(x) = c_v|x − a_v|. Аналогично можно понять, что L_v(x) = max{0, c_v(a_v − x)}.

Выразим S_v(x) через L_2v(x) и L_2v+1(x) (то есть функцию S вершины v через функции L её детей). Верно следующее соотношение:

S_v(x) = c_v|x − a_v| + L_2v(x) + L_2v+1(x).

Действительно, если в вершину v мы ставим значение x, то мы платим, во-первых, за изменение самой вершины v, и во-вторых, мы должны поменять поддеревья v каким-то образом, чтобы значение в v оказалось не меньше значений в её детях, а эту стоимость мы можем получить из функции L для детей.

L_v(x) мы сейчас научимся считать по S_v(x). Но давайте в этом месте остановимся и выскажем предположение, какой вид имеют функции L_v и S_v. Можно догадаться, что они будут кусочно-линейными функциями переменной x, но на самом деле верно даже более сильное условие: они будут выпуклыми кусочно-линейными функциями (другими словами, угол наклона каждого следующего звена возрастает). Давайте строго это докажем: пусть это верно для вершин 2v и 2v + 1. Тогда S_v(x), как следует из формулы выше, тоже выпуклая кусочно-линейная функция (так как является суммой трёх выпуклых кусочно-линейных функций).

Теперь уже L_v(x) легко получить по S_v(x): рассмотрим точку глобального минимума S_v(x). До этой точки S_v(x) убывает, а после неё возрастает. Для того, чтобы получить L_v(x), надо просто заменить участок возрастания S_v(x) на константный горизонтальный участок со значением, равным глобальному минимуму функции S_v(x).

Заметим, что для того, чтобы задать функции L_v и S_v, нужно O(size(v)) информации о точках излома этих функций, где size(v) — это размер поддерева вершины v. Действительно, точек излома в графике функции S_v(x) не больше, чем суммарно точек излома в графиках функций S_2v и S_2v+1 плюс ещё одна точка излома из-за слагаемого c_v|x − a_v|. Получается рекуррента T(v) = T(2v) + T(2v + 1) + 1 на количество хранимой в худшем случае информации, решением которой является T(v) = size(v).

Непосредственно реализовать основную формулу, используемую в задаче, можно за линейную сложность от размеров сливаемых функций. Таким образом получается решение за size(v) = nk = n · log₂ n.

---

Задача E. Отделяй и властвуй

Автор задачи: Михаил Тихомиров

Имя входного файла:	Имя выходного файла:	Ограничение по времени:	Ограничение по памяти:
стандартный ввод	стандартный вывод	5 секунд	512 мегабайт

Последовательность чисел называется хорошей, если ее можно построить согласно следующим правилам:

• пустая последовательность является хорошей;
• если X и Y — хорошие последовательности, то XY (конкатенация X и Y) также является
  хорошей;
• если X — хорошая последовательность, а n — любое число, то nXn (число n, потом все элементы X, и, наконец, опять число n) также является хорошей последовательностью.

Например, последовательность (1, 2, 2, 1, 3, 3) является хорошей, а последовательность (1, 2, 1, 2) — нет.

Последовательность называется разделимой, если существует способ разбить ее на две хорошие подпоследовательности (любая из них может быть пустой). Например, последовательность (1, 2, 1, 2) является разделимой (поскольку ее можно разбить на хорошие подпоследовательности (1, 1) и (2, 2)), а последовательность (1, 2, 3, 1, 2, 3) — нет.

Рассмотрим все последовательности из 2n чисел, такие что каждое число от 1 до n встречается ровно дважды. Сколько из них являются разделимыми? Найдите ответ по модулю 10⁹ + 7.

Формат входных данных

В единственной строке ввода записано одно целое число n (1 ⩽ n ⩽ 500).

Формат выходных данных

Выведите одно целое число — ответ на задачу по модулю 10⁹ + 7.

Примеры

стандартный ввод	стандартный вывод
1	1
2	6
4	2016

Разбор задачи E

Как проверить, является ли последовательность отделимой? Для данной последовательности построим граф на n вершинах. Вершины i и j соединим ребром, если пары соответствующих чисел нельзя включить в одну ПСП (т. е., например, когда числа расположены как (i, j, i, j) либо (j, i, j, i), но не (i, i, j, j) или (i, j, j, i)). Последовательность отделима тогда и только тогда, когда получившийся граф двудолен.

Обозначим за f(n) количество отделимой последовательностей из n пар чисел, при этом последовательности, отличающиеся перенумеровкой чисел, мы будем считать одинаковыми. Введем вспомогательную функцию g(n) — количество примитивных последовательностей, т. е. отделимой последовательностей из n пар чисел, для которых существуют ровно один способ разделения на две ПСП (это в точности те же последовательности, для которых граф, описанный выше, связен).

Пусть мы знаем значения g(n), вычислим теперь f(n). Для произвольной отделимой последовательности рассмотрим компоненту связности, содержащую первое число. Пусть она содержит k пар чисел, тогда между ее элементами есть 2k промежутков, в каждый из которых можно поставить любую отделимой последовательность независимо друг от друга. Обозначим F (n, k) количество способов выбрать k отделимых последовательностей суммарной длины 2n. Тогда из рассуждений выше получаем f(n) = g(k) F(n − k, 2k). Величины F(n, k) тривиально пересчитываются друг через друга и очередные значения f(n).

Как найти g(n)? Назовем конфигурацией спобов разбить 2n элементов на два множества и построить ПСП на каждом из них независимо. Количество конфигураций на 2n элементах t(n) вычисляется тривиально. Вычтем из этого количества все конфигурации, не относящиеся к примитивным последовательностям, оставшееся количество будет равно 2g(n). Снова рассмотрим компоненту связности, содержащую первое число, пусть в ней k пар чисел. Количество таких конфигураций равно 2g(k) T(n − k, 2k), где T (n, k) — количество способов выбрать k конфигураций с суммарным количеством элементов 2n. Таким образом, g(n) = (T(n) − g(k) T(n − k, 2k). Величины T(n, k) вычисляются тривиально через t(n), которые находятся явно. Суммарная сложность этого решения O(n³).

---

Задача F. Дроби

Автор задачи: Олег Христенко

Имя входного файла:	Имя выходного файла:	Ограничение по времени:	Ограничение по памяти:
стандартный ввод	стандартный вывод	2 секунды	512 мегабайт

Задана последовательность a₁, a₂,…, a_n, элементы a_i которой являются дробями, записанными в виде p/q, где p — целое, а q — целое положительное (при этом их взаимная простота не гарантируется).
Проверьте, что для каждой пары i,j (1 ⩽ i < j ⩽ n) существует как минимум одно 1 ⩽ k ⩽ n такое, что a_i · a_j =a_k.

Формат входных данных

Первая строка входных данных содержит одно целое число n (1 ⩽ n ⩽ 3 · 10⁵) — длину последовательности. В следующей строке записаны n дробей в формате p/q (p и q целые, |p| ⩽ 10⁹, 1 ⩽ q ⩽ 10⁹).

Формат выходных данных

Выведите «Yes», если для каждой пары различных i и j найдётся требуемое k, и «No» в противном случае.

Примеры

стандартный ввод	стандартный вывод
1 7/42	Yes
3 3/3 0/1 -5/5	Yes
2 2/1 3/2	No

Разбор задачи F

Сократим все дроби. Произведём несколько наблюдений.

Во-первых, если какое-то число встречается более чем два раза, то можно удалить все его копии
кроме двух: это не повлияет на множество всевозможных попарных произведений.

Во-вторых, заметим, что в каждом из множеств 0 < |x| < 1 и 1 < |x| есть не более одно го числа. Действительно, если, например, на 0 < |x| < 1 есть больше одного числа, то выберем из всех представленных там чисел два минимальных по абсолютному значению (скажем, a и b), возьмём их произведение ab, и оно будет иметь ещё меньшее ненулевое абсолютное значение: 0 < |ab| = |a||b| < min{|a|, |b|}, а значит, оно не совпадает ни с одним из чисел в нашем множестве. Аналогично с диапазоном 1 < |x|.

Таким образом, после сокращения и удаления дубликатов при условии, что ответ — Yes, в нашем множестве может быть не более восьми чисел: два нуля, две единицы, две минус единицы и по одному числу из указанных диапазонов. Значит, можно придерживаться следующей логики: сократим все числа, оставим от каждого числа не более двух его копий. Если получилось больше восьми чисел, то ответ однозначно No, иначе можно рассмотреть все пары чисел, благо их совсем немного, и честно проверить требуемое условие.