Алгоритм BM25 / Хабр
Впервые данный алгоритм встретил на Википедии и не обратил на него особого внимания. Позже изучая научные труды сотрудников Яндекса, я обратил внимание на то, что они ссылаются на него, например, в статье Сегаловича об алгоритмах определения нечетких дубликатов, поэтому решил разобраться, в чем смысл его использования. Постараюсь на простых примерах это объяснить. Итак, для чего этот алгоритм?
Первое. Вводится зависимость релевантности от вхождения или не вхождения слов в запросах с более чем одного слова.
Пусть есть несколько запросов состоящих из нескольких слов, например (пример чисто иллюстративный):
- купить смартфон Samsung
- купить смартфон Samsung Galaxy
Пусть сравниваются два документы (опять же иллюстративно) и первый документ не содержит слова Galaxy. Согласно расчетов оценка релевантности эта сума релевантностей каждого из слов.
Релевантность каждого из слова равна его IDF * на второй множитель в выражении выше. Релевантность всего поискового запроса равна сумме релевантностей всех слов. Таким образом, отсутствие слова или другими словами (его частота) равна 0 дает релевантность 0. Поэтому если по двум первым словам score будет одинаково то более релевантным будет тот документ, который содержит слово Galaxy.
Второе. Преимущество при поиске в запросах с более чем 2-ух слов, одно из которых менее употребительно (более узкоспециализированное) будет отдаваться документам которые содержат это узкоспециализированное слово. Например, есть запрос купить Samsung Galaxy Note 2 (чисто иллюзорный пример). Пусть Note 2 – это более редкое слово (меньше раз встречается в коллекции чем Samsung и Galaxy). Пусть есть 2-а документа каждый из которых релевантен запросу и каждый из них содержит кроме Samsung и Galaxy также Note 2. При этом в первом документе note 2 употребляется только один раз, тогда как во втором – 3 раза (подразумевается, что документ содержит больше информации о Note 2).
Обратите также внимание, что из-за того, что количество документов содержащее слово Note 2 меньше равно в 50 раз от содержащих слово galaxy (500) мы получаем IDF равный 3,279634 что значительно больше IDF для слова galaxy.
Пока что у нас были одинаковые значения частот для слова note 2 (для других слов также). Теперь давайте в Excel увеличим частотность слова note 2 для док2, вместо 0,02 сделаем 0,05 (5 вхождений слова).
Обратите внимание, что значение IDF не изменяется но значение формула (второй множитель на изображении в самом вверху) теперь стало равно 0,061856 и именно это значение участвует в вычислении score, которое теперь для док2 равно уже 0,290559
Теперь самое главное. Увеличим частоту вхождения слова galaxy до 5 в док 1
Как мы видим суммарная частота каждого из слов в док1 и док2 одинакова. Но значение score (релевантность) выше у док2, потому что слово note2 является более редко встречающимся соответственно его результирующее влияние больше чем слово galaxy.
Но значение score (релевантность) выше у док2, потому что слово note2 является более редко встречающимся соответственно его результирующее влияние больше чем слово galaxy.
На практике наличие слов в многосложных запросах очень важно. Конечно же релевантность современных поисковых систем определяется не только исходя из частот как это было показано на примере формулы BM25, но все же некоторые корреляции провести можно. В основном это касается того, что если в документе нет слова из поискового запроса то такому документу значительно сложнее подняться в ТОП по запросу по сравнению с теми, у которых это слово содержится. Давайте рассмотрим пример на поисковой системе Яндекс.
Вводим запрос Samsung galaxy. У меня выдача касалась Samsung galaxy в целом (2 сайта, как обычно Википедия) остальное модели, картинки и т.д.
Вводим запрос samsung galaxy note 2. Выдача полностью меняется, теперь представлены страницы, которые содержат информацию не просто о Samsung galaxy, а о Samsung galaxy note 2.
Вводим запрос samsung galaxy note 2 ценаОпять выдача меняется теперь в выдаче страницы, которые уже содержат слово цена, а не просто Samsung galaxy.
Вводим запрос samsung galaxy note 2 цена Харьков. Выдача кардинально меняется, все страницы в ТОП10 содержат слово Харьков.
Можно ли сказать, что слово Харьков является более узкоспециализированным, как это приводилось в алгоритме BM25 выше? IDF cлова Харьков знает только поисковая система, но в контексте поискового запроса Samsung galaxy note 2 оно без сомнения сужает область поиска. Может быть пример с Яндексом немного неудачен, в силу того, что в приведенном случае большую роль будет играть учет региональности запроса, но я думаю со мной согласится любой сеошник, что слово из поискового запроса обязательно должно быть в тексте, я же всего лишь постарался показать работу алгоритма BM25 и раскрыть 2-а важных его аспекта.
Ссылка на xls документ — книга11.xls
Настройка алгоритма оценки — Azure Cognitive Search
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 3 мин
В зависимости от возраста службы поиска Когнитивный поиск Azure поддерживает два алгоритма оценки для назначения релевантности результатам полнотекстового поискового запроса:
- Алгоритм Okapi BM25 , используемый во всех службах поиска, созданных после 15 июля 2020 г.

- Классический алгоритм сходства, используемый всеми службами поиска, созданными до 15 июля 2020 г.
Рейтинг BM25 — это рейтинг по умолчанию, так как он, как правило, создает рейтинги поиска, которые лучше соответствуют ожиданиям пользователей. Он включает параметры для настройки результатов на основе таких факторов, как размер документа. Для служб поиска, созданных после июля 2020 года, BM25 является единственным алгоритмом оценки. Если вы попытаетесь задать «сходство» с ClassicSimilarity в новой службе, будет возвращена ошибка HTTP 400, так как этот алгоритм не поддерживается службой.
Для старых служб классический алгоритм сходства остается алгоритмом по умолчанию. Старые службы могут обновляться до BM25 по индексу. При переключении с классической модели на BM25 можно увидеть некоторые различия в упорядочении результатов поиска.
Задание параметров BM25
Сходство BM25 добавляет два параметра для управления вычислением оценки релевантности.
PUT [service-name].search.windows.net/indexes/[index-name]?api-version=2020-06-30&allowIndexDowntime=true
{
"similarity": {
"@odata.type": "#Microsoft.Azure.Search.BM25Similarity",
"b" : 0.5,
"k1" : 1.3
}
}
Так как Когнитивный поиск не позволяет обновлять динамический индекс, необходимо перевести индекс в автономный режим, чтобы можно было добавить параметры. Индексирование и запросы завершаются ошибкой, пока индекс находится в автономном режиме. Длительность сбоя — это время, необходимое для обновления индекса, обычно не более нескольких секунд. После завершения обновления индекс возвращается автоматически. Чтобы перевести индекс в автономный режим, добавьте параметр URI allowIndexDowntime=true в запрос, который задает свойство «сходство».
Справочник по свойствам BM25
| Свойство | Тип | Описание |
|---|---|---|
| k1 | number | Управляет функцией взвешивания частоты употребления каждого термина для конечной оценки релевантности пары «документ-запрос». Диапазон значений: 0,0–3,0. Значение по умолчанию: 1,2. Значение 0,0 представляет собой «двоичную модель», где вклад одного соответствующего термина одинаков для всех соответствующих документов, независимо от того, сколько раз этот термин отображается в тексте, в то время как большее значение k1 позволяет оценке продолжать увеличиваться по мере того, как в документе найдено больше экземпляров того же термина. Использование более высокого значения k1 может быть важным в случаях, когда ожидается, что несколько терминов будут частью поискового запроса. В таких случаях мы скорее отдадим предпочтение документам, которые содержат много различных терминов из поискового запроса,чем тем, в которых один нужный термин встречается несколько раз. Например, при запросе индекса для документов, содержащих термины “Космическая программа “Аполлон”, будет лучше, если оценка статьи о греческой мифологии, где слово “Аполлон” встречается несколько десятков раз, но нет упоминаний о “космической программе”, будет меньше, чем у статьи, в которой хотя бы пару раз явно упоминается и “Аполлон”, и “космическая программа”. Диапазон значений: 0,0–3,0. Значение по умолчанию: 1,2. Значение 0,0 представляет собой «двоичную модель», где вклад одного соответствующего термина одинаков для всех соответствующих документов, независимо от того, сколько раз этот термин отображается в тексте, в то время как большее значение k1 позволяет оценке продолжать увеличиваться по мере того, как в документе найдено больше экземпляров того же термина. Использование более высокого значения k1 может быть важным в случаях, когда ожидается, что несколько терминов будут частью поискового запроса. В таких случаях мы скорее отдадим предпочтение документам, которые содержат много различных терминов из поискового запроса,чем тем, в которых один нужный термин встречается несколько раз. Например, при запросе индекса для документов, содержащих термины “Космическая программа “Аполлон”, будет лучше, если оценка статьи о греческой мифологии, где слово “Аполлон” встречается несколько десятков раз, но нет упоминаний о “космической программе”, будет меньше, чем у статьи, в которой хотя бы пару раз явно упоминается и “Аполлон”, и “космическая программа”. |
| b | number | Определяет зависимость оценки релевантности от длины документа. Диапазон значений: 0–1. Значение по умолчанию: 0,75. Значение 0,0 означает, что длина документа не влияет на оценку, а значение 1,0 означает, что влияние частоты терминов на оценку релевантности будет нормализовано по длине документа. Нормализация частоты терминов по длине документа полезна в тех случаях, когда мы хотим наказать более длинные документы. В некоторых случаях более длинные документы (например, объемный роман) содержат много ненужных терминов в сравнении с более короткими документами. |
Включение оценки BM25 в старых службах
Если вы используете службу поиска, созданную с марта 2014 по 15 июля 2020 г., можно включить BM25, задав для новых индексов свойство «сходство». Свойство предоставляется только для новых индексов, поэтому, если требуется BM25 для существующего индекса, необходимо удалить и перестроить индекс со свойством сходства, для которого задано значение Microsoft. Azure.Search.BM25Similarity.
Azure.Search.BM25Similarity.
После того как индекс существует со свойством «сходство», можно переключаться между BM25Similarity или ClassicSimilarity.
Следующие ссылки описывают свойство сходства в пакетах Azure SDK.
| Клиентская библиотека | Свойство сходства |
|---|---|
| .NET | SearchIndex.Similarity |
| Java | SearchIndex.setSimilarity |
| JavaScript | SearchIndex.Similarity |
| Python | свойство сходства для SearchIndex |
Пример REST
Можно также использовать REST API. В следующем примере создается новый индекс со свойством «сходство», равным BM25:
PUT [service-name].search.windows.net/indexes/[index name]?api-version=2020-06-30
{
"name": "indexName",
"fields": [
{
"name": "id",
"type": "Edm.String",
"key": true
},
{
"name": "name",
"type": "Edm. String",
"searchable": true,
"analyzer": "en.lucene"
},
...
],
"similarity": {
"@odata.type": "#Microsoft.Azure.Search.BM25Similarity"
}
}
String",
"searchable": true,
"analyzer": "en.lucene"
},
...
],
"similarity": {
"@odata.type": "#Microsoft.Azure.Search.BM25Similarity"
}
}
См. также:
- Сходство и оценка в Когнитивном поиске Azure
- Справочник по REST API
- Добавление профилей повышения в индекс
- Создание API индекса
- Библиотеки службы «Поиск Azure» для .NET
Принцип алгоритмов TF-IDF и BM25 и реализация на Python
Теги: Обработка естественного языка
TF-IDF — это аббревиатура от английского термина Frequency-Inverse Document Frequency, а на китайском языке — Term Frequency-Inverse Document Frequency.
Сходство TF-IDF между вопросом пользователя и стандартным вопросом — это сумма значений TF-IDF, вычисленных для каждого слова в вопросе пользователя и стандартном вопросе. Рассчитывается следующим образом:
Алгоритм TF-IDF быстрее вычисляется, но у него есть недостатки: поскольку он учитывает только частоту слов и не отражает статус словаря в контексте текста, он не может хорошо выделить семантическую информацию.
import numpy as np
class TF_IDF_Model(object):
def __init__(self, documents_list):
self.documents_list = documents_list
self.documents_number = len(documents_list)
self.tf = []
self.idf = {}
self.init()
def init(self):
df = {}
for document in self.documents_list:
temp = {}
for word in document:
temp[word] = temp.get(word, 0) + 1/len(document)
self.tf.append(temp)
for key in temp.keys():
df[key] = df.get(key, 0) + 1
for key, value in df.items():
self.idf[key] = np.log(self.documents_number / (value + 1))
def get_score(self, index, query):
score = 0.0
for q in query:
if q not in self.tf[index]:
continue
score += self.tf[index][q] * self.idf[q]
return score
def get_documents_score(self, query):
score_list = []
for i in range(self.documents_number):
score_list. append(self.get_score(i, query))
return score_list
append(self.get_score(i, query))
return score_listimport numpy as np
from collections import Counter
class BM25_Model(object):
def __init__(self, documents_list, k1=2, k2=1, b=0.5):
self.documents_list = documents_list
self.documents_number = len(documents_list)
self.avg_documents_len = sum([len(document) for document in documents_list]) / self.documents_number
self.f = []
self.idf = {}
self.k1 = k1
self.k2 = k2
self.b = b
self.init()
def init(self):
df = {}
for document in self.documents_list:
temp = {}
for word in document:
temp[word] = temp.get(word, 0) + 1
self.f.append(temp)
for key in temp.keys():
df[key] = df.get(key, 0) + 1
for key, value in df.items():
self.idf[key] = np.log((self.documents_number - value + 0.5) / (value + 0.5))
def get_score(self, index, query):
score = 0. 0
document_len = len(self.f[index])
qf = Counter(query)
for q in query:
if q not in self.f[index]:
continue
score += self.idf[q] * (self.f[index][q] * (self.k1 + 1) / (
self.f[index][q] + self.k1 * (1 - self.b + self.b * document_len / self.avg_documents_len))) * (
qf[q] * (self.k2 + 1) / (qf[q] + self.k2))
return score
def get_documents_score(self, query):
score_list = []
for i in range(self.documents_number):
score_list.append(self.get_score(i, query))
return score_list
0
document_len = len(self.f[index])
qf = Counter(query)
for q in query:
if q not in self.f[index]:
continue
score += self.idf[q] * (self.f[index][q] * (self.k1 + 1) / (
self.f[index][q] + self.k1 * (1 - self.b + self.b * document_len / self.avg_documents_len))) * (
qf[q] * (self.k2 + 1) / (qf[q] + self.k2))
return score
def get_documents_score(self, query):
score_list = []
for i in range(self.documents_number):
score_list.append(self.get_score(i, query))
return score_list
Интеллектуальная рекомендация
Весенние облако (2) Зул Интеллектуальный маршрут: приложение веб-сервлета в природе маршрутизаторов и фильтров
Маршрутизация компонента системы Micro Service. Например, / может отображаться на ваше веб-приложение, / API / карту пользователя на службу пользователя и карту / API / магазин в магазин. От официальн…
От официальн…
Настроить PagersliidingTabstrip Выбор статуса для изменений цветов
Каждая ошибка — это возможность улучшить себя. На этот раз вы должны поговорить о проблемах, встречающихся в PagersLidingTabstrip. Цвет и т. Д. Итак, что я должен установить здесь? Верхняя часть кода:…
[Массив] [Динамическое планирование] Меч относится к максимуму и
[Онлайн программирование]Максимум и 【Описание проблемы】 Гц время от времени возьмите несколько профессиональных вопросов для мерцания этих некоммерческих профессиональных одноклассников. Сегодня, посл…
Исключение Java
Исключение Java Исключительная система наследования Throwable Причина исключения бросить ключевое слово бросает ключевое слово попробуй поймай наконец ключевое слово RuntimeException Сведения об исклю…
Пиньинь (луогу р1012)
Описание заголовка Есть n натуральных чисел (n≤20), которые соединены в строку, чтобы сформировать наибольшее многозначное целое число. Например: когда n = 3, максимальное целое число из 3 целых чи…
Например: когда n = 3, максимальное целое число из 3 целых чи…
Вам также может понравиться
CMD DEBUG JS CODE
Чтобы сделать плавные заметки здесь, нам удобно отладить код JS. Когда проект не нужен, код JS может быть отладкой, когда доступ к браузере будет доступен! Подготовьте файл JS 2. CMD Откройте среду об…
Инкапсуляция и разбиение на страницы уровня Node Dao
Традиционный способ письма В этом случае мы видим, что пользователь должен подключаться к базе данных каждый раз, когда он работает. В этом случае эффективность очень низкая, поэтому мы инкапсулируем …
Последовательный алгоритм хеширования и рукописная упрощенная версия последовательного алгоритма хеширования
Последовательный алгоритм хеширования: На основе алгоритма Hash реализован алгоритм согласованного хеширования, который используется для решения проблемы точек доступа в Интернете и динамического разд…
Значение контекста Tomcat initializeContext (). Lookup () параметр
Я часто вижу операции на jndi 1. lookup («java: comp / env») получить информацию о конфигурации контейнера приложения envContext 2. Получить тест источника данных в конфигурации env конфигура…
lookup («java: comp / env») получить информацию о конфигурации контейнера приложения envContext 2. Получить тест источника данных в конфигурации env конфигура…
Активизация коммерциализации автономного вождения Gaode анонсирует технологическую дорожную карту высокоточных карт
26 июля в Пекине состоялся Саммит будущего транспорта 2018 года, организованный Gaode Maps. На авто-специальном форуме, посвященном теме «Навстречу будущему», Gaode Map впервые продемонстр…
Практический BM25 — Часть 2: Алгоритм BM25 и его переменные
Это второй пост в серии из трех частей Практический BM25 о ранжировании сходства (релевантности). Если вы только присоединяетесь, ознакомьтесь с Часть 1: Как осколки влияют на оценку релевантности в Elasticsearch. Алгоритм BM25 в происходящее. Сначала посмотрим на формулу, потом разобью каждый компонент на понятные части:
Мы видим несколько общих компонентов, таких как q i , IDF(q i ), f(q i ,D), k1, b и кое-что о длинах полей. Вот о чем каждый из них:
Вот о чем каждый из них:
- q i — это i th термин запроса.
Например, если я ищу «шейн», будет только 1 термин запроса, поэтому q 0 — это «шейн». Если я ищу «shane connelly» на английском языке, Elasticsearch увидит пробел и разметит это как 2 термина: q 0 будет «шейн», а q 1 будет «коннелли». Эти термины запроса подключаются к другим битам уравнения, и все они суммируются.
- IDF(g i ) – это обратная частота документа для i -го -го термина запроса.
Для тех, кто раньше работал с TF/IDF, концепция IDF может быть вам знакома. Если нет, не беспокойтесь! (И если это так, обратите внимание, что существует разница между формулой IDF в TF/IDF и IDF в BM25.) Компонент IDF нашей формулы измеряет, как часто термин встречается во всех документах, и «штрафует» термины, которые являются общими. . Фактическая формула, используемая Lucene/BM25 для этой части:
Где docCount — это общее количество документов, которые имеют значение для поля в сегменте (по сегментам, если вы используетеsearch_type=dfs_query_then_fetch) и f(q i ) — количество документов, содержащих i th термин запроса. В нашем примере мы видим, что «шейн» встречается во всех 4 документах, поэтому для термина «шейн» мы получаем IDF («шейн»):
В нашем примере мы видим, что «шейн» встречается во всех 4 документах, поэтому для термина «шейн» мы получаем IDF («шейн»):
Однако мы видим, что «коннелли» появляется только в 2 документах, поэтому мы получаем IDF («коннелли»):
Здесь мы видим, что запросы, содержащие эти более редкие термины («коннелли» встречается реже, чем «шейн» в нашем корпусе из 4 документов), имеют более высокий множитель, поэтому они вносят больший вклад в итоговую оценку. Это имеет интуитивно понятный смысл: термин «the», вероятно, встречается почти в каждом документе на английском языке, поэтому, когда пользователь ищет что-то вроде «слон», «слон», вероятно, важнее — и мы хотим, чтобы он вносил больший вклад в поисковый запрос. оценка — чем термин «the» (который будет почти во всех документах). - Мы видим, что длина поля делится на среднюю длину поля в знаменателе как fieldLen/avgFieldLen.
Мы можем рассматривать это как длину документа относительно средней длины документа.
 Если документ длиннее среднего, знаменатель увеличивается (уменьшается оценка), а если он короче среднего, знаменатель уменьшается (увеличивается оценка). Обратите внимание, что реализация длины поля в Elasticsearch основана на количестве терминов (а не на чем-то другом, например, на длине символа). Это точно так, как описано в исходной статье BM25, хотя у нас есть специальный флаг (discount_overlaps) для обработки синонимов, если вы того пожелаете. Об этом можно думать следующим образом: чем больше терминов в документе — по крайней мере, не соответствующих запросу — тем ниже оценка документа. Опять же, это имеет интуитивный смысл: если документ состоит из 300 страниц и в нем один раз упоминается мое имя, он с меньшей вероятностью будет иметь такое же отношение ко мне, как короткий твит, в котором я упоминается один раз.
Если документ длиннее среднего, знаменатель увеличивается (уменьшается оценка), а если он короче среднего, знаменатель уменьшается (увеличивается оценка). Обратите внимание, что реализация длины поля в Elasticsearch основана на количестве терминов (а не на чем-то другом, например, на длине символа). Это точно так, как описано в исходной статье BM25, хотя у нас есть специальный флаг (discount_overlaps) для обработки синонимов, если вы того пожелаете. Об этом можно думать следующим образом: чем больше терминов в документе — по крайней мере, не соответствующих запросу — тем ниже оценка документа. Опять же, это имеет интуитивный смысл: если документ состоит из 300 страниц и в нем один раз упоминается мое имя, он с меньшей вероятностью будет иметь такое же отношение ко мне, как короткий твит, в котором я упоминается один раз. - Мы видим переменную b, которая появляется в знаменателе и умножается на коэффициент длины поля, который мы только что обсуждали. Чем больше b, тем сильнее влияние длины документа по сравнению со средней длиной.
 Чтобы убедиться в этом, вы можете представить, что если вы установите b равным 0, эффект соотношения длины будет полностью сведен на нет, и длина документа не будет иметь никакого отношения к оценке. По умолчанию b имеет значение 0,75 в Elasticsearch.
Чтобы убедиться в этом, вы можете представить, что если вы установите b равным 0, эффект соотношения длины будет полностью сведен на нет, и длина документа не будет иметь никакого отношения к оценке. По умолчанию b имеет значение 0,75 в Elasticsearch. - Наконец, мы видим две составляющие оценки, которые проявляются как в числителе, так и в знаменателе: k1 и f(q i ,D). Их внешний вид с обеих сторон затрудняет понимание того, что они делают, просто взглянув на формулу, но давайте быстро перейдем к делу.
- f(q i ,D) — «сколько раз термин запроса i th встречается в документе D?»
Во всех этих документах f(«shane»,D) равно 1, но f(«connelly»,D) различается: 1 для документов 3 и 4, но 0 для документов 1 и 2. Если бы было 5 -й -й документ с текстом «shane shane» будет иметь значение f («shane», D) равное 2. Мы видим, что
f(q i ,D) находится как в числителе, так и в знаменателе, и есть специальный множитель «k1», о котором мы поговорим далее.
 Если рассматривать f(q i ,D), то чем больше терминов запроса встречается в документе, тем выше будет его оценка. Это имеет интуитивно понятный смысл: документ, в котором наше имя упоминается много раз, с большей вероятностью будет связан с нами, чем документ, в котором оно упоминается только один раз.
Если рассматривать f(q i ,D), то чем больше терминов запроса встречается в документе, тем выше будет его оценка. Это имеет интуитивно понятный смысл: документ, в котором наше имя упоминается много раз, с большей вероятностью будет связан с нами, чем документ, в котором оно упоминается только один раз. - k1 — это переменная, которая помогает определить характеристики насыщения частоты термина. То есть он ограничивает, насколько один термин запроса может повлиять на оценку данного документа. Это достигается путем приближения к асимптоте. Вы можете увидеть сравнение BM25 с TF/IDF в этом:
Большее/меньшее значение k1 означает, что наклон кривой «tf() of BM25» изменяется. Это влияет на изменение того, как «термины, встречающиеся больше раз, добавляют дополнительные баллы». Интерпретация k1 заключается в том, что для документов средней длины именно значение частоты термина дает половину максимального балла для рассматриваемого термина. Кривая влияния tf на счет быстро растет, когда tf() ≤ k1, и все медленнее и медленнее, когда tf() > k1.
Продолжая наш пример, с k1 мы контролируем ответ на вопрос «насколько больше должно добавление второго «шейна» к документу способствовать оценке, чем первое или третье по сравнению со вторым?» Более высокий k1 означает, что оценка для каждого термина может продолжать расти относительно больше для большего количества экземпляров этого термина. Значение 0 для k1 будет означать, что все, кроме IDF(q i ) отменяется. По умолчанию k1 имеет значение 1,2 в Elasticsearch.
- f(q i ,D) — «сколько раз термин запроса i th встречается в документе D?»
Во всех этих документах f(«shane»,D) равно 1, но f(«connelly»,D) различается: 1 для документов 3 и 4, но 0 для документов 1 и 2. Если бы было 5 -й -й документ с текстом «shane shane» будет иметь значение f («shane», D) равное 2. Мы видим, что
f(q i ,D) находится как в числителе, так и в знаменателе, и есть специальный множитель «k1», о котором мы поговорим далее.
Пересматривая наш поиск с нашими новыми знаниями
Мы удалим наш индекс людей и воссоздадим его всего с 1 сегментом, чтобы нам не пришлось использовать search_type=dfs_query_then_fetch . Мы проверим наши знания, установив три индекса: один со значением k1 для 0 и b для 0,5 и второй индекс (люди2) со значением b для 0 и k1 для 10 и третий индекс (люди3) со значением b до 1 и k1 до 5.
УДАЛИТЬ людей
ПОСТАВИТЬ людей
{
"настройки": {
"количество_осколков": 1,
"индекс" : {
"сходство" : {
"дефолт" : {
"тип": "BM25",
«б»: 0,5,
"к1": 0
}
}
}
}
}
ПОСТАВИТЬ людей2
{
"настройки": {
"количество_осколков": 1,
"индекс" : {
"сходство" : {
"дефолт" : {
"тип": "BM25",
"б": 0,
«Л1»: 10
}
}
}
}
}
ПОСТАВИТЬ людей3
{
"настройки": {
"количество_осколков": 1,
"индекс" : {
"сходство" : {
"дефолт" : {
"тип": "BM25",
"б": 1,
«к1»: 5
}
}
}
}
}
Теперь добавим несколько документов во все три индекса:
POST люди/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди2/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди3/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди2/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди3/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
Теперь, когда мы делаем:
ПОЛУЧИТЬ /люди/_поиск
{
"запрос": {
"соответствие": {
"название": "Шейн"
}
}
}
Мы видим у людей, что все документы имеют оценку 0,074107975. Это соответствует нашему пониманию установки k1 на 0: для оценки имеет значение только IDF поискового запроса!
Это соответствует нашему пониманию установки k1 на 0: для оценки имеет значение только IDF поискового запроса!
Теперь проверим people2, у которого b = 0 и k1 = 10:
ПОЛУЧИТЬ /people2/_search
{
"запрос": {
"соответствие": {
"название": "Шейн"
}
}
}
Из результатов этого поиска следует сделать вывод о двух вещах.
Во-первых, мы видим, что результаты упорядочены исключительно по количеству появлений «шейн». Документы 1, 2, 3 и 4 получили «шейн» один раз и, таким образом, имеют одинаковую оценку 0,074107975. Документ 5 имеет «шейн» дважды, поэтому имеет более высокий балл (0,13586462) благодаря f («шейн», D5) = 2, а документ 6 снова имеет более высокий балл (0,18812023) благодаря f («шейн», D6) = 3. Это согласуется с нашей интуицией, когда мы устанавливаем b равным 0 в people2: длина — или общее количество терминов в документе — не влияет на оценку; только количество и релевантность совпадающих терминов.
Во-вторых, следует отметить, что разница между этими оценками нелинейна, хотя для этих 6 документов она кажется довольно близкой к линейной.
- Разница в оценке между NO вхождениями из нашего поискового термина и первым — 0,074107975
- Разница в оценке между добавлением секунды нашего поискового термина, а первая — 0,13586462 — 0,074107975 = 0,06117566664596462 — 0,074107975 = 0,06117566664596462 — 0,074107975 = 0,06117666664596462 — 0,074107975 = 0,0617566666645962 — 0,074107975. разница между добавлением третье вхождение нашего поискового запроса, а второе 0,18812023 — 0,13586462 = 0,05225561
0,074107975 довольно близко к 0,061756645, что очень близко к 0,05225561, но они явно уменьшаются. Причина, по которой это выглядит почти как линейных, заключается в том, что k1 велико. По крайней мере, мы можем видеть, что оценка не увеличивается линейно с дополнительными вхождениями — если бы они были, мы ожидали бы увидеть ту же разницу с каждым дополнительным термином. Мы вернемся к этой идее после проверки людей3.
Теперь проверим people3, у которого k1 = 5 и b = 1:
GET /people3/_search
{
"запрос": {
"соответствие": {
"название": "Шейн"
}
}
}
Возвращаем следующие хиты:
"попадания": [
{
"_index": "люди3",
"_тип": "_doc",
"_id": "1",
"_score": 0,16674294,
"_источник": {
"title": "Шейн"
}
},
{
"_index": "люди3",
"_тип": "_doc",
"_id": "6",
"_score": 0,10261105,
"_источник": {
"title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли"
}
},
{
"_index": "люди3",
"_тип": "_doc",
"_id": "2",
"_score": 0,102611035,
"_источник": {
"title": "Шейн Си"
}
},
{
"_index": "люди3",
"_тип": "_doc",
"_id": "4",
"_score": 0,102611035,
"_источник": {
"title": "Шейн Коннелли"
}
},
{
"_index": "люди3",
"_тип": "_doc",
"_id": "5",
"_score": 0,102611035,
"_источник": {
"title": "Шейн Шейн Коннелли Коннелли"
}
},
{
"_index": "люди3",
"_тип": "_doc",
"_id": "3",
"_score": 0,074107975,
"_источник": {
"title": "Шейн П. Коннелли"
}
}
]
Коннелли"
}
}
]
Мы можем видеть на примере людей3, что теперь отношение совпадающих терминов («шейн») к несовпадающим — это единственное, что влияет на относительную оценку. Таким образом, такие документы, как документ 3, в котором только 1 термин соответствует из 3 баллов ниже 2, 4, 5 и 6, все из которых соответствуют ровно половине терминов, и все они имеют меньшие баллы, чем документ 1, который точно соответствует документу.
Опять же, мы можем отметить, что существует «большая» разница между документами с наивысшей оценкой и документами с более низкой оценкой для людей2 и людей3. Это благодаря (опять же) большому значению k1. В качестве дополнительного упражнения попробуйте удалить людей2/людей3 и снова установить для них что-то вроде k1 = 0,01, и вы увидите, что оценки между документами с меньшим количеством документов меньше. При b = 0 и k1 = 0,01:
- The score difference between having no occurrences of our search term and the first is 0.
 074107975
074107975 - The score difference between adding a second occurrence of our search term and the first is 0.074476674 — 0.074107975 = 0.000368699
- The score разница между добавлением третьего вхождения нашего поискового термина и второго составляет 0,07460038 — 0,074476674 = 0,000123706
Таким образом, при k1 = 0,01 мы видим, что влияние оценки каждого дополнительного вхождения падает намного быстрее, чем при k1 = 5 или k1 = 10. 4 9Вхождение 0027-й добавит к счету гораздо меньше, чем 3 -й -й и так далее. Другими словами, при этих меньших значениях k1 показатели термина насыщаются намного быстрее. Как мы и ожидали!
Надеюсь, это поможет увидеть, что эти параметры делают с различными наборами документов. Обладая этими знаниями, мы затем перейдем к тому, как выбрать подходящие b и k1 и как Elasticsearch предоставляет инструменты для понимания оценок и повторения вашего подхода.
Продолжите эту серию: Часть 3: Рекомендации по выбору b и k1 в Elasticsearch
Понимание TF-IDF и BM-25 — KMW Technology
Введение
Эта статья предназначена для специалистов по поиску, которые хотят получить глубокое понимание функций ранжирования TF-IDF и BM25 (также называемых «сходствами» в Lucene). ). Если вы похожи на многих практиков, вы уже знакомы с TF-IDF, но когда вы впервые увидели сложную формулу BM25, вы подумали «может быть, позже». Пришло время, наконец, понять это! Вы, наверное, слышали, что BM25 похож на TF-IDF, но на практике работает лучше. Эта статья покажет вам, как именно BM25 основывается на TF-IDF, какие у него параметры и почему он так эффективен. Если вы предпочитаете пропустить математику и работать с практическими примерами, демонстрирующими поведение BM25, ознакомьтесь с нашей сопутствующей статьей «Понимание оценки на примерах».
). Если вы похожи на многих практиков, вы уже знакомы с TF-IDF, но когда вы впервые увидели сложную формулу BM25, вы подумали «может быть, позже». Пришло время, наконец, понять это! Вы, наверное, слышали, что BM25 похож на TF-IDF, но на практике работает лучше. Эта статья покажет вам, как именно BM25 основывается на TF-IDF, какие у него параметры и почему он так эффективен. Если вы предпочитаете пропустить математику и работать с практическими примерами, демонстрирующими поведение BM25, ознакомьтесь с нашей сопутствующей статьей «Понимание оценки на примерах».
Обзор TF-IDF
Давайте рассмотрим TF-IDF, попробовав разработать его с нуля. Представьте, что мы создаем поисковую систему. Предположим, у нас уже есть способ найти документы, которые соответствуют запросу пользователя. Теперь нам нужна функция ранжирования , которая подскажет нам, как упорядочить эти документы. Чем выше оценка документа по этой функции, тем выше мы поместим его в списке результатов, которые мы возвращаем пользователю.
Целью TF-IDF и аналогичных функций ранжирования является вознаграждение релевантность . Допустим, пользователь ищет слово «собаки». Если Документ 1 больше относится к теме собак, чем Документ 2, то мы хотим, чтобы оценка Документа 1 была выше, чем оценка Документа 2, поэтому мы сначала покажем лучший результат, и пользователь будет доволен. Насколько выше должна быть оценка Документа 1? На самом деле это не имеет значения, если порядок оценок соответствует порядку релевантности.
Вы можете быть немного шокированы дерзостью того, что мы пытаемся сделать: мы попытаемся оценить релевантность миллионов или миллиардов документов, используя математическую функцию, ничего не зная о человеке, который делает это. поиска, причем фактически не читая документы и не понимая, о чем они! Как это возможно?
Мы сделаем простое, но чрезвычайно полезное предположение. Мы предполагаем, что чем больше раз документ содержит термин, тем больше вероятность того, что он будет о этом термине. Другими словами, мы будем использовать частоту термина (TF) , количество вхождений термина в документе, в качестве показателя релевантности. Это единственное предположение открывает нам путь к решению, казалось бы, невозможной проблемы с помощью простой математики. Наше предположение не идеально, и иногда оно идет очень неправильно, но оно работает достаточно часто, чтобы быть полезным. Итак, с этого момента мы будем рассматривать частоту терминов как благо — то, что мы хотим вознаграждать.
Другими словами, мы будем использовать частоту термина (TF) , количество вхождений термина в документе, в качестве показателя релевантности. Это единственное предположение открывает нам путь к решению, казалось бы, невозможной проблемы с помощью простой математики. Наше предположение не идеально, и иногда оно идет очень неправильно, но оно работает достаточно часто, чтобы быть полезным. Итак, с этого момента мы будем рассматривать частоту терминов как благо — то, что мы хотим вознаграждать.
TF-IDF: попытка 1
В качестве отправной точки для нашей функции ранжирования давайте сделаем самое простое из возможных. Мы установим оценку документа, равную его частоте терминов. Если мы ищем термин T и оцениваем релевантность документа D, то:
score(D, T) = termFrequency(D, T)
Когда запрос содержит несколько терминов, например «собаки и кошки, Как мы должны справиться с этим? Должны ли мы попытаться проанализировать взаимосвязь между различными терминами, а затем сложным образом смешать баллы по каждому термину? Не так быстро! Самый простой подход — просто сложить баллы за каждый термин вместе. Так и будем делать, будем надеяться на лучшее. Если у нас есть многотерминальный запрос Q, то мы установим:
Так и будем делать, будем надеяться на лучшее. Если у нас есть многотерминальный запрос Q, то мы установим:
score(D, Q) = сумма по всем терминам T в Q в score(D, T)
Насколько хорошо работает наша простая функция ранжирования? К сожалению, у него есть некоторые проблемы:
1) Более длинные документы получают несправедливое преимущество перед более короткими, потому что в них больше места для включения большего количества вхождений термина, даже если они могут быть не более релевантными этому термину. Давайте пока проигнорируем эту проблему.
2) Все термины в запросе обрабатываются одинаково, без учета того, какие из них более значимы или важны. Когда мы суммируем баллы за каждый термин вместе, незначительные термины, такие как «и» и «то», которые встречаются очень часто, будут доминировать в объединенном балле. Допустим, вы ищете «слоны и коровы». Возможно, в указателе есть единственный документ, включающий все три термина («слоны», «и», «коровы»), но вместо того, чтобы сначала увидеть этот идеальный результат, вы видите документ, в котором «и» встречается больше всего — может быть, у него 10 000 из них. Это предпочтение слов-заполнителей явно не то, что нам нужно.
Это предпочтение слов-заполнителей явно не то, что нам нужно.
TF-IDF: Попытка 2
Чтобы предотвратить доминирование слов-заполнителей, нам нужен способ оценки важности терминов в запросе. Поскольку мы не можем закодировать понимание естественного языка в нашу функцию оценки, мы попытаемся найти прокси для важности. Лучше всего выбрать редкость . Если термин не встречается в большинстве документов корпуса, то всякий раз, когда он встречается, мы предполагаем, что это появление значимо. С другой стороны, если термин встречается в большинстве документов нашего корпуса, то присутствие этого термина в любом конкретном документе теряет свою ценность как показатель релевантности.
Таким образом, высокая частота терминов — это хорошо, но ее достоинства компенсируются высокой частотой документов (DF) — количеством документов, содержащих термин — что мы будем считать плохим.
Чтобы обновить нашу функцию таким образом, чтобы она вознаграждала частоту терминов, но снижала частоту документов, мы могли бы попробовать разделить TF на DF:
score(D, T) = termFrequency(D, T) / docFrequency(T)
Что не так с этим? К сожалению, DF сам по себе ничего нам не говорит. Если DF для термина «слон» равен 100, то является ли термин «слон» редким термином или общепринятым термином? Это зависит от размера корпуса. Если корпус содержит 100 документов, «слон» — обычное явление, если он содержит 100 000 документов, «слон» — редкость.
Если DF для термина «слон» равен 100, то является ли термин «слон» редким термином или общепринятым термином? Это зависит от размера корпуса. Если корпус содержит 100 документов, «слон» — обычное явление, если он содержит 100 000 документов, «слон» — редкость.
TF-IDF: Попытка 3
Вместо того, чтобы рассматривать DF отдельно, давайте посмотрим на N/DF, где N — размер поискового индекса или корпуса. Обратите внимание, что N/DF является низким для общеупотребительных терминов (100 вхождений слова «слон» в корпусе размером 100 дадут N/DF = 1) и высоким для редких (100 вхождений «слон» в корпусе размером 100 000 будет дают N/DF = 1000). Это именно то, чего мы хотим: совпадения для распространенных терминов должны получать низкие баллы, а совпадения для редких терминов — высокие. Наша улучшенная формула может выглядеть так:
score(D, T) = termFrequency(D, T) * (N / docFrequency(T))
Нам лучше, но давайте подробнее посмотрим, как ведет себя N/DF. Допустим, у нас есть 100 документов, и в одном из них встречается слово «слон», а в двух — слово «жираф». Оба термина одинаково редки, но значение N/DF для слона будет равно 100, а для жирафа будет вдвое меньше, т.е. 50. Если совпадение для жирафа получит половину оценки соответствия для слона только потому, что частота документирования жирафа на единицу выше, чем у слона ? Штраф за одно дополнительное появление слова в корпусе кажется слишком высоким. Возможно, если у нас есть 100 документов, не должно иметь большого значения, равен ли DF термина 1, 2, 3 или 4 .
Допустим, у нас есть 100 документов, и в одном из них встречается слово «слон», а в двух — слово «жираф». Оба термина одинаково редки, но значение N/DF для слона будет равно 100, а для жирафа будет вдвое меньше, т.е. 50. Если совпадение для жирафа получит половину оценки соответствия для слона только потому, что частота документирования жирафа на единицу выше, чем у слона ? Штраф за одно дополнительное появление слова в корпусе кажется слишком высоким. Возможно, если у нас есть 100 документов, не должно иметь большого значения, равен ли DF термина 1, 2, 3 или 4 .
TF-IDF: Попытка 4
Как мы видели, когда DF находится в очень низком диапазоне, небольшие различия в DF могут иметь существенное влияние на N/DF и, следовательно, на оценку. Мы могли бы сгладить снижение N/DF, когда DF находится в нижней части своего диапазона. Один из способов сделать это — взять журнал N/DF. Если бы мы захотели, мы могли бы попробовать использовать здесь другую функцию сглаживания, но функция log проста и делает то, что нам нужно. На этой диаграмме сравниваются N/DF и log(N/DF), предполагая, что N=100:
На этой диаграмме сравниваются N/DF и log(N/DF), предполагая, что N=100:
Назовем log(N/DF) обратную частоту документа (IDF) термина. Теперь наша функция ранжирования может быть выражена как TF * IDF или:
score(D, T) = termFrequency(D, T) * log(N / docFrequency(T))
Мы пришли к традиционному определению TF. -IDF, и хотя мы сделали несколько смелых предположений, на практике эта функция работает довольно хорошо: она накопила длинный послужной список успешного применения в поисковых системах. Мы закончили или можем сделать еще лучше?
Разработка BM25
Как вы могли догадаться, мы не готовы останавливаться на TF-IDF. В этом разделе мы создадим функцию BM25, которую можно рассматривать как улучшение TF-IDF. Мы сохраним ту же структуру формулы TF * IDF, но заменим компоненты TF и IDF уточнениями этих значений.
Шаг 1: Насыщение сроков
Мы говорили, что TF — это хорошо, и наша формула TF-IDF действительно вознаграждает это. Но если в документе 200 вхождений слова «слон», действительно ли это 9 0003 дважды так же актуален, как и документ, содержащий 100 вхождений? Можно утверждать, что если слово «слон» встречается достаточно много раз, скажем, 100, то документ почти наверняка релевантен, и любые дальнейшие упоминания не увеличивают вероятность релевантности. Иными словами, когда документ насыщен вхождений термина, большее количество вхождений не должно оказывать существенного влияния на оценку. Поэтому нам нужен способ контролировать вклад TF в наш счет. Мы хотели бы, чтобы этот вклад быстро увеличивался, когда TF мал, а затем увеличивался медленнее, приближаясь к пределу, когда TF становится очень большим.
Но если в документе 200 вхождений слова «слон», действительно ли это 9 0003 дважды так же актуален, как и документ, содержащий 100 вхождений? Можно утверждать, что если слово «слон» встречается достаточно много раз, скажем, 100, то документ почти наверняка релевантен, и любые дальнейшие упоминания не увеличивают вероятность релевантности. Иными словами, когда документ насыщен вхождений термина, большее количество вхождений не должно оказывать существенного влияния на оценку. Поэтому нам нужен способ контролировать вклад TF в наш счет. Мы хотели бы, чтобы этот вклад быстро увеличивался, когда TF мал, а затем увеличивался медленнее, приближаясь к пределу, когда TF становится очень большим.
Один из распространенных способов приручить TF — извлечь из него квадратный корень, но это все равно неограниченная величина. Мы хотели бы сделать что-то более изощренное. Мы хотели бы установить ограничение на вклад TF в счет, и мы хотели бы иметь возможность контролировать, насколько быстро вклад приближается к этому пределу.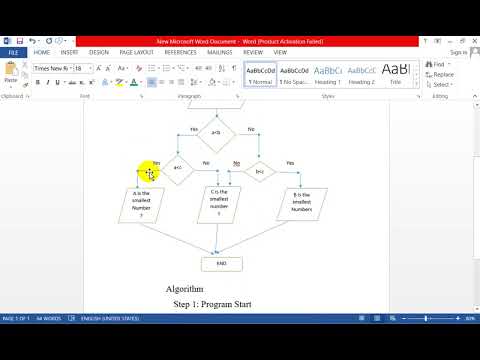 Было бы неплохо, если бы у нас был параметр k , который мог бы управлять формой этой кривой насыщения? Таким образом, мы сможем поэкспериментировать с различными значениями k и посмотреть, что лучше всего подходит для конкретного корпуса.
Было бы неплохо, если бы у нас был параметр k , который мог бы управлять формой этой кривой насыщения? Таким образом, мы сможем поэкспериментировать с различными значениями k и посмотреть, что лучше всего подходит для конкретного корпуса.
Для этого мы проделаем трюк. Вместо того, чтобы использовать необработанный TF в нашей формуле ранжирования, мы будем использовать значение:
TF / (TF + k)
Если для k установлено значение 1, будет сгенерирована последовательность 1/2, 2/3, 3/ 4, 4/5, 5/6 по мере того, как TF увеличивается на 1, 2, 3 и т. д. Обратите внимание, как эта последовательность растет быстро в начале, а затем медленнее, приближаясь к 1 с меньшими и меньшими приращениями. Это то, чего мы хотим. Теперь, если мы изменим k на 2, мы получим 1/3, 2/4, 3/5, 4/6, которые растут немного медленнее. Вот график формулы TF/(TF + k) для k = 1, 2, 3, 4:
Этот трюк TF/(TF + k) действительно является основой BM25. Это позволяет нам контролировать вклад TF в счет настраиваемым образом.
Дополнительно: насыщение терминов и многотерминальные запросы
Удачным побочным эффектом использования TF/(TF + k) для учета насыщения терминов является то, что мы в конечном итоге награждаем полные совпадения по сравнению с частичными. Другими словами, мы отдаем предпочтение документам, которые соответствуют большему количеству терминов в многотерминальном запросе, а не документам, которые имеют много совпадений только для одного из терминов.
Предположим, что «кошка» и «собака» имеют одинаковые значения IDF. Если мы ищем «кошка-собака», мы хотели бы, чтобы документ, содержащий по одному экземпляру каждого термина, работал лучше, чем документ, в котором есть два экземпляра «кошка» и ни одного «собака». Если бы мы использовали необработанный TF, они оба получили бы одинаковую оценку. Но давайте сделаем наш улучшенный расчет, предполагая, что k=1. В нашем документе «кошка-собака» «кошка» и «собака» имеют TF = 1, поэтому каждый будет вносить TF/(TF + 1) = 1/2 в оценку, что в сумме составляет 1. В нашем Документ «кошка кошка», «кошка» имеет TF 2, поэтому она будет вносить TF/(TF+1) = 2/3 в оценку. Документ «кошка-собака» выигрывает, потому что «кошка» и «собака» вносят больший вклад, когда каждое встречается один раз, чем «кошка», когда встречается дважды.
В нашем Документ «кошка кошка», «кошка» имеет TF 2, поэтому она будет вносить TF/(TF+1) = 2/3 в оценку. Документ «кошка-собака» выигрывает, потому что «кошка» и «собака» вносят больший вклад, когда каждое встречается один раз, чем «кошка», когда встречается дважды.
Предполагая, что IDF двух терминов одинакова, всегда лучше иметь один экземпляр каждого термина, чем два экземпляра одного из них.
Шаг 2: Длина документа
Теперь давайте вернемся к проблеме, которую мы пропустили при первом создании TF-IDF: длина документа. Если документ оказался очень коротким и в нем один раз встречается слово «слон», это хороший показатель того, что слово «слон» важно для содержимого. Но если документ очень-очень длинный и в нем упоминается слон только один раз, вероятно, документ не о слонах. Поэтому мы хотели бы вознаграждать совпадения в коротких документах и наказывать совпадения в длинных документах. Как мы можем этого добиться?
Во-первых, мы должны решить, что означает для документа быть коротким или длинным. Нам нужна система отсчета, поэтому мы будем использовать сам корпус в качестве нашей системы отсчета. Короткий документ – это документ, который на 90 003 короче, чем в среднем на 90 006 для всего корпуса.
Нам нужна система отсчета, поэтому мы будем использовать сам корпус в качестве нашей системы отсчета. Короткий документ – это документ, который на 90 003 короче, чем в среднем на 90 006 для всего корпуса.
Вернемся к нашему фокусу TF/(TF + k). Конечно, по мере увеличения k значение TF/(TF + k) уменьшается. Чтобы наказать длинные документы, мы можем увеличить k, если документ длиннее среднего, и уменьшить его, если документ короче среднего. Мы добьемся этого, умножив k на отношение дл/адл . Здесь dl — длина документа, а adl — средняя длина документа по всему корпусу.
Когда документ средней длины, dl/adl =1, и наш множитель вообще не влияет на k. Для документа короче среднего мы будем умножать k на значение от 0 до 1, тем самым уменьшая его и увеличивая TF/(TF+k). Для документа, который длиннее среднего, мы будем умножать k на значение больше 1, тем самым увеличивая его и уменьшая TF/(TF+k). Множитель также ставит нас на другую кривую насыщения TF. Более короткие документы будут приближаться к точке насыщения TF быстрее, в то время как более длинные документы будут приближаться к ней более постепенно.
Более короткие документы будут приближаться к точке насыщения TF быстрее, в то время как более длинные документы будут приближаться к ней более постепенно.
Шаг 3: Параметризация длины документа
В предыдущем разделе мы обновили нашу функцию ранжирования, чтобы учесть длину документа, но всегда ли это хорошая идея? Насколько большое значение мы должны придавать длине документа в любом конкретном корпусе? Могут ли быть какие-то наборы документов, где длина имеет большое значение, а в каких нет? Мы могли бы рассматривать важность длины документа как второй параметр, с которым мы можем поэкспериментировать.
Мы собираемся добиться этой настраиваемости с помощью другого трюка. Мы добавим новый параметр b в смесь (должно быть между 0 и 1). Вместо умножения k на dl/adl, как мы делали раньше, мы умножим k на следующее значение на основе dl/adl и b:
1 – b + b*dl/adl
Что это нам дает ? Вы можете видеть, что если b равно 1, мы получаем (1 – 1 + 1*dl/adl), и это сводится к множителю, который у нас был раньше, dl/adl. С другой стороны, если b равно 0, все становится равным 1, а длина документа вообще не учитывается. Когда b увеличивается от 0 до 1, множитель быстрее реагирует на изменения в dl/adl. На приведенной ниже диаграмме показано, как ведет себя наш множитель при росте dl/adl, когда b=0,2 по сравнению с b=0,8.
С другой стороны, если b равно 0, все становится равным 1, а длина документа вообще не учитывается. Когда b увеличивается от 0 до 1, множитель быстрее реагирует на изменения в dl/adl. На приведенной ниже диаграмме показано, как ведет себя наш множитель при росте dl/adl, когда b=0,2 по сравнению с b=0,8.
Резюме: Fancy TF
Напомним, что мы работали над изменением термина TF в TF * IDF, чтобы он реагировал на насыщенность терминов и длину документа. Чтобы учесть насыщение терминов, мы ввели прием TF/(TF + k). Чтобы учесть длину документа, мы добавили множитель (1 – b + b*dl/adl). Теперь вместо того, чтобы использовать необработанный TF в нашей функции ранжирования, мы используем эту «причудливую» версию TF:
TF/(TF + k*(1 - b + b*dl/adl))
Вспомним, что k — ручка, управляющая кривой насыщения термина, а b — ручка, управляющая важностью длины документа.
Действительно, это версия TF, используемая в BM25. И поздравляю: если вы дочитали до этого места, теперь вы понимаете все самое интересное о BM25.
Шаг 4: Причудливый или не такой причудливый IDF
Мы еще не закончили, мы должны вернуться к тому, как BM25 обрабатывает частоту документов. Раньше мы определяли IDF как log(N/DF), но BM25 определяет его как:
log((N - DF + .5)/(DF + .5))
В чем разница?
Как вы могли заметить, мы разрабатывали нашу функцию подсчета очков с помощью набора эвристик. Исследователи в области информационного поиска хотели поставить функции ранжирования на более строгую теоретическую основу, чтобы они могли на самом деле доказывать что-то об их поведении, а не просто экспериментировать и надеяться на лучшее. Чтобы вывести теоретически обоснованную версию IDF, исследователи взяли то, что называется весом Робертсона-Спарка-Джонса, сделали упрощающее предположение и получили log (N-DF+0,5)/(DF+0,5). Мы не будем вдаваться в подробности, а просто сосредоточимся на практической значимости этой разновидности IDF. .5 здесь мало что делают, поэтому давайте просто рассмотрим log (N-DF)/DF, который иногда называют «вероятностным IDF». Здесь мы сравниваем нашу ванильную IDF с вероятностной IDF, где N=10.
Здесь мы сравниваем нашу ванильную IDF с вероятностной IDF, где N=10.
Вы можете видеть, что вероятностный IDF резко падает для терминов, которые есть в большинстве документов. Это может быть желательно, потому что, если термин действительно существует в 98 % документов, он, вероятно, является стоп-словом, таким как «и» или «или», и он должен иметь гораздо, гораздо меньший вес, чем термин, который очень распространен, например, в 70 % документов. документы, но все еще не совсем вездесущи.
Загвоздка в том, что log (N-DF)/DF отрицателен для терминов, которые находятся более чем в половине корпуса. (Помните, что функция журнала становится отрицательной при значениях от 0 до 1.) Мы не хотим, чтобы отрицательные значения выходили из нашей функции ранжирования, потому что наличие термина запроса в документе никогда не должно учитываться при поиске — оно никогда не должно приводить к ошибке. более низкий балл, чем если бы термин просто отсутствовал. Чтобы предотвратить отрицательные значения, реализация Lucene BM25 добавляет 1 следующим образом:
IDF = log (1 + (N - DF + .5)/(DF + .5))
Эта 1 может показаться невинной модификацией, но она полностью меняет поведение формулы! Если мы снова забудем об этих надоедливых .5 и заметим, что добавление 1 равносильно добавлению DF/DF, вы увидите, что формула сводится к ванильной версии IDF, которую мы использовали раньше: log (N/DF).
log (1 + (N - DF + 0,5)/(DF + 0,5)) ≈ log (1 + (N - DF)/DF ) = log (DF/DF + (N - DF)/DF) = log ((DF + N - DF)/DF) = журнал (N/DF)
Итак, хотя кажется, что BM25 использует причудливую версию IDF, на практике (как это реализовано в Lucene) он в основном использует ту же старую версию IDF, которая используется в традиционных TF/IDF, без ускоренного снижения для высоких значений DF.
Обналичивание
Мы готовы извлечь выгоду из нашего нового понимания, взглянув на результат объяснения запроса Lucene. Вы увидите что-то вроде этого:
«оценка (частота = 3,0), произведение:» «idf, рассчитанный как log (1 + (N — n + 0,5) / (n + 0,5)) из:» «tf, вычисляется как freq / (freq + k1 * (1 — b + b * dl / avgdl)) из:»
Наконец-то мы готовы понять эту абракадабру. Вы можете видеть, что Lucene использует продукт TF*IDF, где TF и IDF имеют свои специальные определения BM25. Нижняя буква n здесь означает DF. Термин IDF — это якобы причудливая версия, которая оказывается такой же, как и традиционная IDF, N/n.
Вы можете видеть, что Lucene использует продукт TF*IDF, где TF и IDF имеют свои специальные определения BM25. Нижняя буква n здесь означает DF. Термин IDF — это якобы причудливая версия, которая оказывается такой же, как и традиционная IDF, N/n.
Термин TF основан на нашем трюке с насыщением: частота/(частота + k). Использование k1 вместо k в выводе объяснения историческое — это происходит из того времени, когда в формуле было более одного k. То, что мы называем необработанным TF, обозначается как частота здесь.
Мы видим, что k1 умножается на коэффициент, который наказывает длину документа выше среднего, но вознаграждает длину документа ниже среднего: (1-b + b *dl/avgdl). То, что мы называли adl, здесь обозначено как avgdl .
И, конечно же, мы видим, что есть параметры, для которых по умолчанию установлено значение k=1,2 и b = 0,75 в Lucene. Вам, вероятно, не нужно будет настраивать их, но вы можете, если хотите.
Таким образом, простой TF-IDF вознаграждает за частоту терминов и штрафует за частоту документов. BM25 выходит за рамки этого, чтобы учитывать длину документа и насыщенность частоты терминов.
Стоит отметить, что до того, как Lucene представила BM25 в качестве функции ранжирования по умолчанию в версии 6, она реализовала TF-IDF с помощью так называемой функции практической оценки, которая представляла собой набор улучшений (включая «координат» и нормализацию длины поля). это сделало TF-IDF более похожим на BM25. Таким образом, разница в поведении, которую можно было бы наблюдать, когда Lucene переключилась на BM25, была, вероятно, менее существенной, чем если бы Lucene все время использовала чистый TF-IDF. В любом случае, все согласны с тем, что BM25 — это улучшение, и теперь вы понимаете, почему.
Если вы работаете поисковым инженером, наиболее вероятным местом, где вы встретите детали формулы BM25, будут выходные данные объяснения Lucene. Однако, если вы углубитесь в теоретические статьи или прочитаете статью Википедии о BM25, вы увидите, что это уравнение записано в виде такого уравнения:
Надеюсь, этот обзор помог вам лучше понять, как работают две самые популярные функции ранжирования поиска. . Спасибо, что следите за нами!
. Спасибо, что следите за нами!
Дополнительная литература
Эта статья следует по стопам некоторых других больших туров BM25, которые там есть. Эти два настоятельно рекомендуется:
BM25. Следующее поколение релевантности Lucene, Дуг Тернбулл.
. Практическая часть BM25. Хорошей отправной точкой является «Структура вероятностной релевантности: BM25 и далее» Робертсона и Сарагосы.
См. также статью «Окапи на TREC-3», где впервые был представлен BM25.
bm25_intro
- 1 Краткий обзор Okapi BM25
- 1.1.
импорт ОС
# path : сохранить текущий путь, чтобы вернуться к нему позже
путь = os.getcwd()
os.chdir(os.path.join(‘..’, ‘notebook_format’))
из форматов импортировать load_style
load_style (plot_style = Ложь)
Исходящий[1]:
Входящий [2]:
os.chdir(путь) импортировать математику импортировать json запросы на импорт # 1. магия в печатной версии # 2. магия, чтобы ноутбук перезагрузил внешние модули python %load_ext водяной знак %load_ext автоперезагрузка %автоперезагрузка 2 %watermark -a 'Ethen' -d -t -v -p запросы
Этен 2018-11-17 17:24:06 CPython 3.
 6.4
IPython 6.4.0
запросы 2.20.1
6.4
IPython 6.4.0
запросы 2.20.1
Проблема, которую пытается решить BM25 (Best Match 25) , аналогична проблеме TFIDF (частота терминов, обратная частота документа), которая представляет наш текст в векторном пространстве (ее можно применить к полю вне текста). , но текст — это то место, где он присутствует больше всего), поэтому мы можем искать/находить похожие документы для данного документа или запроса.
Суть TFIDF заключается в том, что он полагается на два основных фактора, чтобы определить, похож ли документ на наш запрос.
- Частота терминов, также известная как tf: как часто этот термин встречается в документе? 3 раза? 10 раз?
- Обратная частота документа, также известная как idf: измеряет количество документов, в которых появился термин. Затем обратная частота документа (1/df) измеряет, насколько особенным является термин. Является ли этот термин очень редким (встречается только в одном документе) словом? Или относительно распространенный (встречается почти во всех документах)?
Используя эти два фактора, TFIDF измеряет относительную концентрацию термина в данном фрагменте документа.
 Если термин часто встречается в этой статье, но относительно редко встречается в других местах, то оценка TFIDF будет высокой, а документы с более высокой оценкой TFIDF будут считаться очень релевантными для поискового запроса.
Если термин часто встречается в этой статье, но относительно редко встречается в других местах, то оценка TFIDF будет высокой, а документы с более высокой оценкой TFIDF будут считаться очень релевантными для поискового запроса.BM25 улучшает TFIDF, рассматривая релевантность как проблему вероятности. Оценка релевантности, согласно вероятностному поиску информации, должна отражать вероятность того, что пользователь сочтет результат релевантным. Вместо того, чтобы рассказывать, как была получена формула, здесь мы рассмотрим формулу и попробуем переварить ее, чтобы понять, почему она имеет какой-то смысл.
Gaining Intuition for Okapi BM25¶
BM25 (Best Match 25) Функция оценивает каждый документ в корпусе в соответствии с релевантностью документа для конкретного текстового запроса. Для запроса $Q$ с терминами $q_1, \ldots, q_n$ оценка BM25 для документа $D$ составляет: 9n IDF(q_i, D) \frac{f(q_i, D) \cdot (k_1 + 1)}{f(q_i) + k_1 \cdot (1-b + b \cdot |D|/d_{avg}) )} \end{align}
где:
- $f(q_i, D)$ — количество раз, когда термин $q_i$ встречается в документе $D$.

- $|D|$ — количество слов в документе $D$.
- $d_{avg}$ — среднее количество слов в документе.
- $b$ и $k_1$ — это гиперпараметры для BM25.
Давайте разобьем формулу на более мелкие компоненты, чтобы понять, почему она имеет смысл.
- Прежде всего, это $f(q_i, D)$ и $k_1$. $f(q_i, D)$ должно соответствовать нашей интуиции, поскольку это означает, что чем больше раз термин запроса появляется в документе, тем выше будет оценка документа. Интересной частью является параметр $k_1$, который определяет характеристику насыщения частоты члена. Чем выше значение, тем медленнее насыщение. И когда мы говорим о насыщении, мы имеем в виду тот факт, что если термины встречаются больше раз, добавляются дополнительные баллы. Мы можем наблюдать эту уменьшающуюся отдачу по частоте терминов на графике ниже.
- Тогда часть $|D|/d_{avg}$ в знаменателе означает, что документ, который длиннее среднего документа, приведет к большему знаменателю, что приведет к снижению оценки.
 Интуиция подсказывает, что чем больше в документе терминов, не соответствующих нашему входному запросу, тем ниже должна быть оценка документа. Другими словами, если в 300-страничном документе термин запроса упоминается один раз, вероятность того, что он будет иметь такое же отношение к запросу, меньше, чем в коротком твите, в котором запрос упоминается один раз.
Интуиция подсказывает, что чем больше в документе терминов, не соответствующих нашему входному запросу, тем ниже должна быть оценка документа. Другими словами, если в 300-страничном документе термин запроса упоминается один раз, вероятность того, что он будет иметь такое же отношение к запросу, меньше, чем в коротком твите, в котором запрос упоминается один раз.
Из графика выше видно, что более короткие документы достигают асимптоты намного быстрее. Надеюсь, это похоже на нашу интуицию, поскольку чем больше совпадений у нас есть с более короткими документами, тем больше мы уверены в релевантности, тогда как для длинной книги нам может потребоваться больше времени, чтобы добраться до точки, в которой мы чувствуем себя уверенными в том, что книга действительно имеет отношение к заданному запросу.
- Параметр $b$ (граница 0.0 ~ 1.0) в знаменателе умножается на коэффициент длины документа, который мы только что обсуждали. Чем больше $b$, тем сильнее влияние длины документа по сравнению со средней длиной.
 Мы можем себе представить, что если мы установим $b$ в 0, эффект отношения длин будет полностью сведен на нет.
Мы можем себе представить, что если мы установим $b$ в 0, эффект отношения длин будет полностью сведен на нет.
Что касается частотной части обратного документа, ${IDF}(q_i, D)$. Для корпуса с $N$ документами обратная частота документов для термина $q_i$ вычисляется следующим образом:
\начать{выравнивать} \mbox{IDF}(q_i, D) = \log \frac{N — N(q_i) + 0,5}{N(q_i) + 0,5} \end{выравнивание}
, где
- $N(q_i)$ — количество документов в корпусе, содержащих термин $q_i$.
Часть обратной частоты документа очень похожа на часть TFIDF, роль которой состоит в том, чтобы гарантировать, что более редкие слова будут иметь более высокий балл и вносить больший вклад в окончательный балл.
Обратите внимание, что приведенная выше формула IDF имеет недостаток при использовании ее для терминов, встречающихся более чем в половине корпуса, поскольку значение будет отрицательным, что приведет к отрицательному общему баллу.
 например если у нас есть 10 документов в корпусе, и термин «the» появился в 6 из них, его IDF будет $log(10 — 6 + 0,5/6 + 0,5) = log(4,5/6,5)$. Хотя мы можем утверждать, что наша реализация уже должна была удалить эти часто встречающиеся слова, поскольку эти слова в основном используются для формирования полного предложения и не несут особого смысла, различные программы/пакеты по-прежнему вносят различные коррективы, чтобы предотвратить появление отрицательной оценки. например
например если у нас есть 10 документов в корпусе, и термин «the» появился в 6 из них, его IDF будет $log(10 — 6 + 0,5/6 + 0,5) = log(4,5/6,5)$. Хотя мы можем утверждать, что наша реализация уже должна была удалить эти часто встречающиеся слова, поскольку эти слова в основном используются для формирования полного предложения и не несут особого смысла, различные программы/пакеты по-прежнему вносят различные коррективы, чтобы предотвратить появление отрицательной оценки. например- Добавьте 1 к уравнению.
\начать{выравнивать} \mbox{IDF}(q_i) = \log \big( 1 + \frac{N — N(q_i) + 0,5}{N(q_i) + 0,5} \big) \end{align}
- Для термина, который привел к отрицательному значению IDF, замените его небольшим положительным значением, обычно обозначаемым как $\epsilon$
Как и все гиперпараметры в целом, параметры по умолчанию обычно являются хорошей отправной точкой, и нам, вероятно, следует сосредоточиться на настройке других вещей, прежде чем прыгать в кроличью нору настройки гиперпараметров.
 В контексте поиска это может быть связано с тем, что в нашем рейтинге более старые документы оцениваются ниже в таких приложениях, как рейтинг новостей. Но если мы приступим к настройке, не забывайте всегда измерять производительность различных настроек, и следующие вопросы являются общими отправными точками, на которые мы можем ссылаться.
В контексте поиска это может быть связано с тем, что в нашем рейтинге более старые документы оцениваются ниже в таких приложениях, как рейтинг новостей. Но если мы приступим к настройке, не забывайте всегда измерять производительность различных настроек, и следующие вопросы являются общими отправными точками, на которые мы можем ссылаться.- Для $k_1$ мы должны задать вопрос: «Когда, по нашему мнению, терм, вероятно, будет насыщен?» Для очень длинных документов, таких как книги, весьма вероятно, что в произведении несколько раз будет встречаться множество различных терминов, даже если термин не является основным предметом документа. Возможно, в этой ситуации мы не хотим, чтобы термины насыщались так быстро, поэтому предлагается, чтобы $k_1$ обычно стремился к большим числам, когда текст намного длиннее и разнообразнее. С другой стороны, было предложено установить $k_1$ в нижней части. Очень маловероятно, что в наборе коротких твитов будет несколько раз упоминаться термин, не имеющий тесной связи с этим термином.

- Для $b$ мы должны задаться вопросом: «Когда, по нашему мнению, документ может быть очень длинным, а когда это должно препятствовать его релевантности термину?» Документы, которые являются очень конкретными, такими как технические спецификации или патенты, являются длинными, чтобы быть более конкретными по предмету. Их длина вряд ли повлияет на релевантность, и меньший $b$ может быть более подходящим. С другой стороны, документы, затрагивающие несколько разных тем в широком смысле — новостные статьи (политическая статья может касаться экономики, международных отношений и некоторых корпораций), обзоры пользователей и т. д. — часто выигрывают от выбора больше $b$, чтобы нерелевантные темы для поиска пользователя, включая спам и тому подобное, наказывались.
Реализация¶
В [3]:
# мы создадим несколько поддельных текстов для экспериментов. корпус = [ «Человеко-машинный интерфейс для лабораторных компьютерных приложений abc», «Опрос мнения пользователей о времени отклика компьютерной системы», «Система управления пользовательским интерфейсом EPS», «Системные и человеческие системные испытания EPS», «Отношение воспринимаемого пользователем времени отклика к измерению ошибки», «Генерация случайных бинарных неупорядоченных деревьев», 'График пересечения путей в деревьях', «График миноров IV. Ширина деревьев и квазиупорядочение скважин»,
'График несовершеннолетних Опрос'
]
# удаляем стоп-слова и токенизируем их (вероятно, мы хотим сделать еще кое-что
# предварительная обработка нашего текста в реальных условиях, но мы продолжим
# здесь все просто)
стоп-слова = set(['для', 'а', 'из', 'то', 'и', 'к', 'в'])
тексты = [
[дословно в document.lower().split(), если слово не в стоп-словах]
для документа в корпусе
]
# создать словарь подсчета слов, чтобы мы могли удалять слова, которые встречаются только один раз
word_count_dict = {}
для текста в текстах:
для токена в тексте:
word_count = word_count_dict.get (токен, 0) + 1
word_count_dict[токен] = word_count
texts = [[токен для токена в тексте, если word_count_dict[токен] > 1] для текста в текстах]
тексты
Ширина деревьев и квазиупорядочение скважин»,
'График несовершеннолетних Опрос'
]
# удаляем стоп-слова и токенизируем их (вероятно, мы хотим сделать еще кое-что
# предварительная обработка нашего текста в реальных условиях, но мы продолжим
# здесь все просто)
стоп-слова = set(['для', 'а', 'из', 'то', 'и', 'к', 'в'])
тексты = [
[дословно в document.lower().split(), если слово не в стоп-словах]
для документа в корпусе
]
# создать словарь подсчета слов, чтобы мы могли удалять слова, которые встречаются только один раз
word_count_dict = {}
для текста в текстах:
для токена в тексте:
word_count = word_count_dict.get (токен, 0) + 1
word_count_dict[токен] = word_count
texts = [[токен для токена в тексте, если word_count_dict[токен] > 1] для текста в текстах]
тексты
Исходящий[3]:
[['человек', 'интерфейс', 'компьютер'], ['опрос', 'пользователь', 'компьютер', 'система', 'ответ', 'время'], ['eps', 'пользователь', 'интерфейс', 'система'], ['система', 'человек', 'система', 'eps'], ['пользователь', 'ответ', 'время'], ['деревья'], ['график', 'деревья'], ['граф', 'младшие', 'деревья'], ['график', 'второстепенные', 'опрос']]
В [4]:
класс BM25: """ Лучший матч 25. Параметры
----------
k1 : с плавающей запятой, по умолчанию 1,5
b : с плавающей запятой, по умолчанию 0,75
Атрибуты
----------
tf_ : список[dict[str, int]]
Срок Периодичность на документ. Итак, [{'привет': 1}] означает
первый документ содержит термин «привет» 1 раз.
df_ : словарь[str, int]
Документ Периодичность за семестр. т. е. количество документов в
корпус, содержащий термин.
idf_ : dict[str, float]
Частота обратного документа за термин.
doc_len_ : список[целое число]
Количество терминов в документе. Итак, [3] означает первый
документ содержит 3 термина.
corpus_ : список[список[строка]]
Входной корпус.
corpus_size_ : целое число
Количество документов в корпусе.
avg_doc_len_ : с плавающей запятой
Среднее количество терминов для документов в корпусе.
"""
def __init__(самостоятельно, k1=1,5, b=0,75):
я.б = б
сам.k1 = k1
def fit (я, корпус):
"""
Сопоставьте различные статистические данные, необходимые для расчета рейтинга BM25.
Параметры
----------
k1 : с плавающей запятой, по умолчанию 1,5
b : с плавающей запятой, по умолчанию 0,75
Атрибуты
----------
tf_ : список[dict[str, int]]
Срок Периодичность на документ. Итак, [{'привет': 1}] означает
первый документ содержит термин «привет» 1 раз.
df_ : словарь[str, int]
Документ Периодичность за семестр. т. е. количество документов в
корпус, содержащий термин.
idf_ : dict[str, float]
Частота обратного документа за термин.
doc_len_ : список[целое число]
Количество терминов в документе. Итак, [3] означает первый
документ содержит 3 термина.
corpus_ : список[список[строка]]
Входной корпус.
corpus_size_ : целое число
Количество документов в корпусе.
avg_doc_len_ : с плавающей запятой
Среднее количество терминов для документов в корпусе.
"""
def __init__(самостоятельно, k1=1,5, b=0,75):
я.б = б
сам.k1 = k1
def fit (я, корпус):
"""
Сопоставьте различные статистические данные, необходимые для расчета рейтинга BM25. оценка с использованием данного корпуса.
Параметры
----------
корпус: список[список[строка]]
Каждый элемент в списке представляет документ, и каждый документ
представляет собой список терминов.
Возвращает
-------
себя
"""
тф = []
ДФ = {}
ИДФ = {}
doc_len = []
размер_корпуса = 0
для документа в корпусе:
размер_корпуса += 1
doc_len.append (длина (документ))
# вычислить tf (частоту терминов) для каждого документа
частоты = {}
на срок в документе:
term_count = частоты. Получить (термин, 0) + 1
частоты[термин] = число_терминов
tf.append(частоты)
# вычислить df (частоту документов) на терм
для термина, _ в Frequency.items():
df_count = df.get (термин, 0) + 1
df[термин] = df_count
для срока, частота в df.
оценка с использованием данного корпуса.
Параметры
----------
корпус: список[список[строка]]
Каждый элемент в списке представляет документ, и каждый документ
представляет собой список терминов.
Возвращает
-------
себя
"""
тф = []
ДФ = {}
ИДФ = {}
doc_len = []
размер_корпуса = 0
для документа в корпусе:
размер_корпуса += 1
doc_len.append (длина (документ))
# вычислить tf (частоту терминов) для каждого документа
частоты = {}
на срок в документе:
term_count = частоты. Получить (термин, 0) + 1
частоты[термин] = число_терминов
tf.append(частоты)
# вычислить df (частоту документов) на терм
для термина, _ в Frequency.items():
df_count = df.get (термин, 0) + 1
df[термин] = df_count
для срока, частота в df. items():
idf[term] = math.log(1 + (размер_корпуса - частота + 0,5) / (частота + 0,5))
self.tf_ = tf
self.df_ = дф
self.idf_ = idf
self.doc_len_ = doc_len
self.corpus_ = корпус
self.corpus_size_ = размер_корпуса
self.avg_doc_len_ = сумма (doc_len) / размер_корпуса
вернуть себя
поиск по определению (я, запрос):
scores = [self._score(query, index) для индекса в диапазоне(self.corpus_size_)]
обратные баллы
def _score (я, запрос, индекс):
оценка = 0,0
doc_len = self.doc_len_[индекс]
частоты = self.tf_[index]
для термина в запросе:
если термин не в частотах:
Продолжать
частота = частоты [срок]
числитель = self.idf_[термин] * частота * (self.k1 + 1)
знаменатель = частота + self.k1 * (1 - self.b + self.b * doc_len / self.avg_doc_len_)
оценка += (числитель/знаменатель)
обратный счет
items():
idf[term] = math.log(1 + (размер_корпуса - частота + 0,5) / (частота + 0,5))
self.tf_ = tf
self.df_ = дф
self.idf_ = idf
self.doc_len_ = doc_len
self.corpus_ = корпус
self.corpus_size_ = размер_корпуса
self.avg_doc_len_ = сумма (doc_len) / размер_корпуса
вернуть себя
поиск по определению (я, запрос):
scores = [self._score(query, index) для индекса в диапазоне(self.corpus_size_)]
обратные баллы
def _score (я, запрос, индекс):
оценка = 0,0
doc_len = self.doc_len_[индекс]
частоты = self.tf_[index]
для термина в запросе:
если термин не в частотах:
Продолжать
частота = частоты [срок]
числитель = self.idf_[термин] * частота * (self.k1 + 1)
знаменатель = частота + self.k1 * (1 - self.b + self.b * doc_len / self.avg_doc_len_)
оценка += (числитель/знаменатель)
обратный счет
In [5]:
# запросите наш корпус, чтобы увидеть, какой документ более актуален.
 query = 'Пересечение графа опроса и деревьев'
query = [слово в слово в query.lower().split(), если слово не в стоп-словах]
бм25 = бм25()
bm25.fit(тексты)
баллы = bm25.search(запрос)
для оценки, документ в почтовом индексе (оценки, корпус):
счет = раунд (счет, 3)
print(str(оценка) + '\t' + документ)
query = 'Пересечение графа опроса и деревьев'
query = [слово в слово в query.lower().split(), если слово не в стоп-словах]
бм25 = бм25()
bm25.fit(тексты)
баллы = bm25.search(запрос)
для оценки, документ в почтовом индексе (оценки, корпус):
счет = раунд (счет, 3)
print(str(оценка) + '\t' + документ)
0.0 Человеко-машинный интерфейс для лабораторных компьютерных приложений abc 1.025 Опрос мнения пользователей о времени отклика компьютерной системы 0.0 Система управления пользовательским интерфейсом EPS 0,0 Системные и инженерные испытания систем человека для EPS 0,0 Отношение воспринимаемого пользователем времени отклика к измерению ошибки 1.462. Генерация случайных бинарных неупорядоченных деревьев. 2.485. Граф пересечений путей в деревьях 2.161. Миноры графов IV. Ширины деревьев и хорошо квазиупорядочение. 2.507 Несовершеннолетние графы Опрос
В приведенном выше фрагменте кода мы распечатали оценку релевантности BM25 каждого корпуса вместе с исходным текстом, обратите внимание, что он еще не отсортирован в порядке убывания оценки релевантности, что обычно мы хотим сделать в реальных условиях.
 . То есть найти более релевантный документ, отсортировать их в порядке убывания и представить пользователю. Кроме того, здесь мы вычисляем баллы для каждого документа, это становится дорогостоящим в вычислительном отношении, когда мы начинаем иметь большой размер корпуса. Таким образом, поисковая система использует инвертировал индекс , чтобы ускорить процесс. Инвертированный индекс состоит из списка всех уникальных слов, встречающихся в каком-либо документе, а для каждого слова — списка документов, в которых оно встречается, это позволяет нам быстро находить документы, содержащие термин в нашем запросе, и только затем мы вычисляем показатель релевантности для этого меньшего набора отзывов. Эта ссылка содержит хорошее описание этой концепции на высоком уровне.
. То есть найти более релевантный документ, отсортировать их в порядке убывания и представить пользователю. Кроме того, здесь мы вычисляем баллы для каждого документа, это становится дорогостоящим в вычислительном отношении, когда мы начинаем иметь большой размер корпуса. Таким образом, поисковая система использует инвертировал индекс , чтобы ускорить процесс. Инвертированный индекс состоит из списка всех уникальных слов, встречающихся в каком-либо документе, а для каждого слова — списка документов, в которых оно встречается, это позволяет нам быстро находить документы, содержащие термин в нашем запросе, и только затем мы вычисляем показатель релевантности для этого меньшего набора отзывов. Эта ссылка содержит хорошее описание этой концепции на высоком уровне.ElasticSearch BM25¶
Мы можем увидеть BM25 в действии для ранжирования документов с помощью ElasticSearch, эта записная книжка не является учебным пособием по ElasticSearch, так что, надеюсь, читатель немного знаком с этим инструментом, если нет, каждый фрагмент кода содержит ссылки на некоторые полезные ссылки.

Мы будем следовать стандартному процессу создания индекса для хранения наших документов, добавим несколько примеров документов в индекс и предоставим запрос к индексу, чтобы вернуть соответствующие документы, отсортированные в порядке убывания на основе оценки релевантности, которая будет основана на БМ25.
В [8]:
# инструкция по установке # https://www.elastic.co/guide/en/elasticsearch/reference/current/_installation.html # создание индекса # https://www.elastic.co/guide/en/elasticsearch/reference/current/indices-create-index.html настройки = { 'настройки': { 'индекс': { 'количество_осколков': 1, 'количество_реплик': 1, # явно настроить наш алгоритм подобия по умолчанию для использования bm25, # это позволяет использовать его для всех полей 'сходство': { 'дефолт': { «тип»: «BM25» } } } }, # мы будем индексировать наши документы в поле заголовка с помощью анализатора английского языка, # который убирает за нас стоп-слова, стандартный анализатор по умолчанию не имеет # этот шаг предварительной обработки # https://www. elastic.co/guide/en/elasticsearch/reference/current/analysis.html
'отображения': {
# этот ключ является "типом", который будет объяснен в следующем фрагменте кода
'_doc': {
'характеристики': {
'заглавие': {
'тип': 'текст',
'анализатор': 'английский'
}
}
}
}
}
заголовки = {'Тип контента': 'приложение/json'}
ответ = запросы.пут('http://localhost:9200/experiment', data=json.dumps(настройки), заголовки=заголовки)
отклик
elastic.co/guide/en/elasticsearch/reference/current/analysis.html
'отображения': {
# этот ключ является "типом", который будет объяснен в следующем фрагменте кода
'_doc': {
'характеристики': {
'заглавие': {
'тип': 'текст',
'анализатор': 'английский'
}
}
}
}
}
заголовки = {'Тип контента': 'приложение/json'}
ответ = запросы.пут('http://localhost:9200/experiment', data=json.dumps(настройки), заголовки=заголовки)
отклик
Out[8]:
In [9]:
# индексирующий документ # https://www.elastic.co/guide/en/elasticsearch/reference/current/docs-bulk.html # https://www.elastic.co/guide/en/elasticsearch/guide/master/index-doc.html # документ однозначно идентифицируется индексом, типом и идентификатором # стоит отметить, что есть примечание об удалении возможностей # иметь несколько типов под одним индексом, и в дальнейшем тип будет # просто установить в '_doc' # https://www.
 elastic.co/guide/en/elasticsearch/reference/current/removal-of-types.html
URL-адрес = 'http://локальный:9200/эксперимент/_doc'
для документа в корпусе:
# вставляем документ в поле title
данные = {'название': документ}
ответ = запросы. сообщение (url, данные = json.dumps (данные), заголовки = заголовки)
отклик
elastic.co/guide/en/elasticsearch/reference/current/removal-of-types.html
URL-адрес = 'http://локальный:9200/эксперимент/_doc'
для документа в корпусе:
# вставляем документ в поле title
данные = {'название': документ}
ответ = запросы. сообщение (url, данные = json.dumps (данные), заголовки = заголовки)
отклик
Out[9]:
In [10]:
def search(запрос, заголовки): url = 'http://localhost:9200/experiment/_doc/_search' ответ = запросы.получить (url, данные = json.dumps (запрос), заголовки = заголовки) # ответ содержит другую информацию, например, время, затраченное на # возвращаем ответ, здесь нас интересует только совпавший # результаты, которые хранятся в разделе "посещения" search_hits = json.loads(response.text)['попадания']['попадания'] print('Число\tОценка релевантности\tTitle') для idx нажмите enumerate(search_hits): print('%s\t%s\t%s' % (idx + 1, hit['_score'], hit['_source']['title']))В [11]:
# запрос соответствия # https://www.

- 1.1.
импорт ОС
# path : сохранить текущий путь, чтобы вернуться к нему позже
путь = os.getcwd()
os.chdir(os.path.join(‘..’, ‘notebook_format’))
из форматов импортировать load_style
load_style (plot_style = Ложь)



 String",
"searchable": true,
"analyzer": "en.lucene"
},
...
],
"similarity": {
"@odata.type": "#Microsoft.Azure.Search.BM25Similarity"
}
}
String",
"searchable": true,
"analyzer": "en.lucene"
},
...
],
"similarity": {
"@odata.type": "#Microsoft.Azure.Search.BM25Similarity"
}
}
 append(self.get_score(i, query))
return score_list
append(self.get_score(i, query))
return score_list 0
document_len = len(self.f[index])
qf = Counter(query)
for q in query:
if q not in self.f[index]:
continue
score += self.idf[q] * (self.f[index][q] * (self.k1 + 1) / (
self.f[index][q] + self.k1 * (1 - self.b + self.b * document_len / self.avg_documents_len))) * (
qf[q] * (self.k2 + 1) / (qf[q] + self.k2))
return score
def get_documents_score(self, query):
score_list = []
for i in range(self.documents_number):
score_list.append(self.get_score(i, query))
return score_list
0
document_len = len(self.f[index])
qf = Counter(query)
for q in query:
if q not in self.f[index]:
continue
score += self.idf[q] * (self.f[index][q] * (self.k1 + 1) / (
self.f[index][q] + self.k1 * (1 - self.b + self.b * document_len / self.avg_documents_len))) * (
qf[q] * (self.k2 + 1) / (qf[q] + self.k2))
return score
def get_documents_score(self, query):
score_list = []
for i in range(self.documents_number):
score_list.append(self.get_score(i, query))
return score_list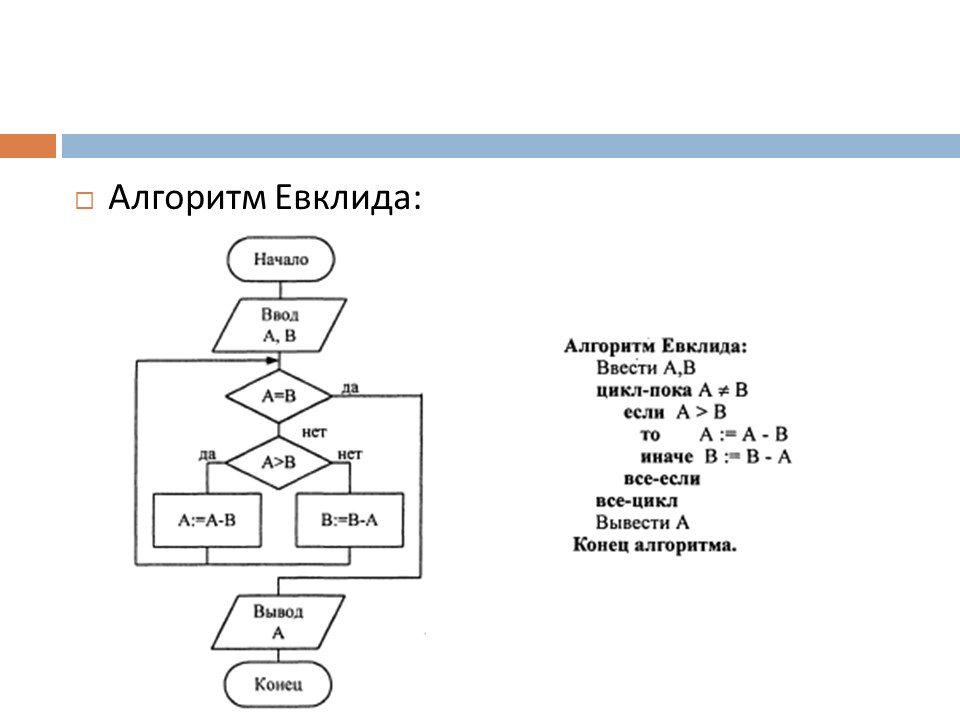 В нашем примере мы видим, что «шейн» встречается во всех 4 документах, поэтому для термина «шейн» мы получаем IDF («шейн»):
В нашем примере мы видим, что «шейн» встречается во всех 4 документах, поэтому для термина «шейн» мы получаем IDF («шейн»): Если документ длиннее среднего, знаменатель увеличивается (уменьшается оценка), а если он короче среднего, знаменатель уменьшается (увеличивается оценка). Обратите внимание, что реализация длины поля в Elasticsearch основана на количестве терминов (а не на чем-то другом, например, на длине символа). Это точно так, как описано в исходной статье BM25, хотя у нас есть специальный флаг (discount_overlaps) для обработки синонимов, если вы того пожелаете. Об этом можно думать следующим образом: чем больше терминов в документе — по крайней мере, не соответствующих запросу — тем ниже оценка документа. Опять же, это имеет интуитивный смысл: если документ состоит из 300 страниц и в нем один раз упоминается мое имя, он с меньшей вероятностью будет иметь такое же отношение ко мне, как короткий твит, в котором я упоминается один раз.
Если документ длиннее среднего, знаменатель увеличивается (уменьшается оценка), а если он короче среднего, знаменатель уменьшается (увеличивается оценка). Обратите внимание, что реализация длины поля в Elasticsearch основана на количестве терминов (а не на чем-то другом, например, на длине символа). Это точно так, как описано в исходной статье BM25, хотя у нас есть специальный флаг (discount_overlaps) для обработки синонимов, если вы того пожелаете. Об этом можно думать следующим образом: чем больше терминов в документе — по крайней мере, не соответствующих запросу — тем ниже оценка документа. Опять же, это имеет интуитивный смысл: если документ состоит из 300 страниц и в нем один раз упоминается мое имя, он с меньшей вероятностью будет иметь такое же отношение ко мне, как короткий твит, в котором я упоминается один раз. Чтобы убедиться в этом, вы можете представить, что если вы установите b равным 0, эффект соотношения длины будет полностью сведен на нет, и длина документа не будет иметь никакого отношения к оценке. По умолчанию b имеет значение 0,75 в Elasticsearch.
Чтобы убедиться в этом, вы можете представить, что если вы установите b равным 0, эффект соотношения длины будет полностью сведен на нет, и длина документа не будет иметь никакого отношения к оценке. По умолчанию b имеет значение 0,75 в Elasticsearch. Если рассматривать f(q i ,D), то чем больше терминов запроса встречается в документе, тем выше будет его оценка. Это имеет интуитивно понятный смысл: документ, в котором наше имя упоминается много раз, с большей вероятностью будет связан с нами, чем документ, в котором оно упоминается только один раз.
Если рассматривать f(q i ,D), то чем больше терминов запроса встречается в документе, тем выше будет его оценка. Это имеет интуитивно понятный смысл: документ, в котором наше имя упоминается много раз, с большей вероятностью будет связан с нами, чем документ, в котором оно упоминается только один раз.
 Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди2/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди3/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди2/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
POST люди3/_doc/_bulk
{ "индекс": { "_id": "1" } }
{ "название": "Шейн" }
{ "индекс": { "_id": "2" } }
{ "название": "Шейн Си" }
{ "индекс": { "_id": "3" } }
{ "title": "Шейн П. Коннелли" }
{ "индекс": { "_id": "4" } }
{ "title": "Шейн Коннелли" }
{ "индекс": { "_id": "5" } }
{ "title": "Шейн Шейн Коннелли Коннелли" }
{ "индекс": { "_id": "6" } }
{ "title": "Шейн Шейн Шейн Коннелли Коннелли Коннелли" }
 Коннелли"
}
}
]
Коннелли"
}
}
]
 074107975
074107975 5)/(DF + .5))
5)/(DF + .5))  6.4
IPython 6.4.0
запросы 2.20.1
6.4
IPython 6.4.0
запросы 2.20.1
 Если термин часто встречается в этой статье, но относительно редко встречается в других местах, то оценка TFIDF будет высокой, а документы с более высокой оценкой TFIDF будут считаться очень релевантными для поискового запроса.
Если термин часто встречается в этой статье, но относительно редко встречается в других местах, то оценка TFIDF будет высокой, а документы с более высокой оценкой TFIDF будут считаться очень релевантными для поискового запроса.
 Интуиция подсказывает, что чем больше в документе терминов, не соответствующих нашему входному запросу, тем ниже должна быть оценка документа. Другими словами, если в 300-страничном документе термин запроса упоминается один раз, вероятность того, что он будет иметь такое же отношение к запросу, меньше, чем в коротком твите, в котором запрос упоминается один раз.
Интуиция подсказывает, что чем больше в документе терминов, не соответствующих нашему входному запросу, тем ниже должна быть оценка документа. Другими словами, если в 300-страничном документе термин запроса упоминается один раз, вероятность того, что он будет иметь такое же отношение к запросу, меньше, чем в коротком твите, в котором запрос упоминается один раз. Мы можем себе представить, что если мы установим $b$ в 0, эффект отношения длин будет полностью сведен на нет.
Мы можем себе представить, что если мы установим $b$ в 0, эффект отношения длин будет полностью сведен на нет. например если у нас есть 10 документов в корпусе, и термин «the» появился в 6 из них, его IDF будет $log(10 — 6 + 0,5/6 + 0,5) = log(4,5/6,5)$. Хотя мы можем утверждать, что наша реализация уже должна была удалить эти часто встречающиеся слова, поскольку эти слова в основном используются для формирования полного предложения и не несут особого смысла, различные программы/пакеты по-прежнему вносят различные коррективы, чтобы предотвратить появление отрицательной оценки. например
например если у нас есть 10 документов в корпусе, и термин «the» появился в 6 из них, его IDF будет $log(10 — 6 + 0,5/6 + 0,5) = log(4,5/6,5)$. Хотя мы можем утверждать, что наша реализация уже должна была удалить эти часто встречающиеся слова, поскольку эти слова в основном используются для формирования полного предложения и не несут особого смысла, различные программы/пакеты по-прежнему вносят различные коррективы, чтобы предотвратить появление отрицательной оценки. например В контексте поиска это может быть связано с тем, что в нашем рейтинге более старые документы оцениваются ниже в таких приложениях, как рейтинг новостей. Но если мы приступим к настройке, не забывайте всегда измерять производительность различных настроек, и следующие вопросы являются общими отправными точками, на которые мы можем ссылаться.
В контексте поиска это может быть связано с тем, что в нашем рейтинге более старые документы оцениваются ниже в таких приложениях, как рейтинг новостей. Но если мы приступим к настройке, не забывайте всегда измерять производительность различных настроек, и следующие вопросы являются общими отправными точками, на которые мы можем ссылаться.
 Ширина деревьев и квазиупорядочение скважин»,
'График несовершеннолетних Опрос'
]
# удаляем стоп-слова и токенизируем их (вероятно, мы хотим сделать еще кое-что
# предварительная обработка нашего текста в реальных условиях, но мы продолжим
# здесь все просто)
стоп-слова = set(['для', 'а', 'из', 'то', 'и', 'к', 'в'])
тексты = [
[дословно в document.lower().split(), если слово не в стоп-словах]
для документа в корпусе
]
# создать словарь подсчета слов, чтобы мы могли удалять слова, которые встречаются только один раз
word_count_dict = {}
для текста в текстах:
для токена в тексте:
word_count = word_count_dict.get (токен, 0) + 1
word_count_dict[токен] = word_count
texts = [[токен для токена в тексте, если word_count_dict[токен] > 1] для текста в текстах]
тексты
Ширина деревьев и квазиупорядочение скважин»,
'График несовершеннолетних Опрос'
]
# удаляем стоп-слова и токенизируем их (вероятно, мы хотим сделать еще кое-что
# предварительная обработка нашего текста в реальных условиях, но мы продолжим
# здесь все просто)
стоп-слова = set(['для', 'а', 'из', 'то', 'и', 'к', 'в'])
тексты = [
[дословно в document.lower().split(), если слово не в стоп-словах]
для документа в корпусе
]
# создать словарь подсчета слов, чтобы мы могли удалять слова, которые встречаются только один раз
word_count_dict = {}
для текста в текстах:
для токена в тексте:
word_count = word_count_dict.get (токен, 0) + 1
word_count_dict[токен] = word_count
texts = [[токен для токена в тексте, если word_count_dict[токен] > 1] для текста в текстах]
тексты
 Параметры
----------
k1 : с плавающей запятой, по умолчанию 1,5
b : с плавающей запятой, по умолчанию 0,75
Атрибуты
----------
tf_ : список[dict[str, int]]
Срок Периодичность на документ. Итак, [{'привет': 1}] означает
первый документ содержит термин «привет» 1 раз.
df_ : словарь[str, int]
Документ Периодичность за семестр. т. е. количество документов в
корпус, содержащий термин.
idf_ : dict[str, float]
Частота обратного документа за термин.
doc_len_ : список[целое число]
Количество терминов в документе. Итак, [3] означает первый
документ содержит 3 термина.
corpus_ : список[список[строка]]
Входной корпус.
corpus_size_ : целое число
Количество документов в корпусе.
avg_doc_len_ : с плавающей запятой
Среднее количество терминов для документов в корпусе.
"""
def __init__(самостоятельно, k1=1,5, b=0,75):
я.б = б
сам.k1 = k1
def fit (я, корпус):
"""
Сопоставьте различные статистические данные, необходимые для расчета рейтинга BM25.
Параметры
----------
k1 : с плавающей запятой, по умолчанию 1,5
b : с плавающей запятой, по умолчанию 0,75
Атрибуты
----------
tf_ : список[dict[str, int]]
Срок Периодичность на документ. Итак, [{'привет': 1}] означает
первый документ содержит термин «привет» 1 раз.
df_ : словарь[str, int]
Документ Периодичность за семестр. т. е. количество документов в
корпус, содержащий термин.
idf_ : dict[str, float]
Частота обратного документа за термин.
doc_len_ : список[целое число]
Количество терминов в документе. Итак, [3] означает первый
документ содержит 3 термина.
corpus_ : список[список[строка]]
Входной корпус.
corpus_size_ : целое число
Количество документов в корпусе.
avg_doc_len_ : с плавающей запятой
Среднее количество терминов для документов в корпусе.
"""
def __init__(самостоятельно, k1=1,5, b=0,75):
я.б = б
сам.k1 = k1
def fit (я, корпус):
"""
Сопоставьте различные статистические данные, необходимые для расчета рейтинга BM25. оценка с использованием данного корпуса.
Параметры
----------
корпус: список[список[строка]]
Каждый элемент в списке представляет документ, и каждый документ
представляет собой список терминов.
Возвращает
-------
себя
"""
тф = []
ДФ = {}
ИДФ = {}
doc_len = []
размер_корпуса = 0
для документа в корпусе:
размер_корпуса += 1
doc_len.append (длина (документ))
# вычислить tf (частоту терминов) для каждого документа
частоты = {}
на срок в документе:
term_count = частоты. Получить (термин, 0) + 1
частоты[термин] = число_терминов
tf.append(частоты)
# вычислить df (частоту документов) на терм
для термина, _ в Frequency.items():
df_count = df.get (термин, 0) + 1
df[термин] = df_count
для срока, частота в df.
оценка с использованием данного корпуса.
Параметры
----------
корпус: список[список[строка]]
Каждый элемент в списке представляет документ, и каждый документ
представляет собой список терминов.
Возвращает
-------
себя
"""
тф = []
ДФ = {}
ИДФ = {}
doc_len = []
размер_корпуса = 0
для документа в корпусе:
размер_корпуса += 1
doc_len.append (длина (документ))
# вычислить tf (частоту терминов) для каждого документа
частоты = {}
на срок в документе:
term_count = частоты. Получить (термин, 0) + 1
частоты[термин] = число_терминов
tf.append(частоты)
# вычислить df (частоту документов) на терм
для термина, _ в Frequency.items():
df_count = df.get (термин, 0) + 1
df[термин] = df_count
для срока, частота в df. items():
idf[term] = math.log(1 + (размер_корпуса - частота + 0,5) / (частота + 0,5))
self.tf_ = tf
self.df_ = дф
self.idf_ = idf
self.doc_len_ = doc_len
self.corpus_ = корпус
self.corpus_size_ = размер_корпуса
self.avg_doc_len_ = сумма (doc_len) / размер_корпуса
вернуть себя
поиск по определению (я, запрос):
scores = [self._score(query, index) для индекса в диапазоне(self.corpus_size_)]
обратные баллы
def _score (я, запрос, индекс):
оценка = 0,0
doc_len = self.doc_len_[индекс]
частоты = self.tf_[index]
для термина в запросе:
если термин не в частотах:
Продолжать
частота = частоты [срок]
числитель = self.idf_[термин] * частота * (self.k1 + 1)
знаменатель = частота + self.k1 * (1 - self.b + self.b * doc_len / self.avg_doc_len_)
оценка += (числитель/знаменатель)
обратный счет
items():
idf[term] = math.log(1 + (размер_корпуса - частота + 0,5) / (частота + 0,5))
self.tf_ = tf
self.df_ = дф
self.idf_ = idf
self.doc_len_ = doc_len
self.corpus_ = корпус
self.corpus_size_ = размер_корпуса
self.avg_doc_len_ = сумма (doc_len) / размер_корпуса
вернуть себя
поиск по определению (я, запрос):
scores = [self._score(query, index) для индекса в диапазоне(self.corpus_size_)]
обратные баллы
def _score (я, запрос, индекс):
оценка = 0,0
doc_len = self.doc_len_[индекс]
частоты = self.tf_[index]
для термина в запросе:
если термин не в частотах:
Продолжать
частота = частоты [срок]
числитель = self.idf_[термин] * частота * (self.k1 + 1)
знаменатель = частота + self.k1 * (1 - self.b + self.b * doc_len / self.avg_doc_len_)
оценка += (числитель/знаменатель)
обратный счет
 query = 'Пересечение графа опроса и деревьев'
query = [слово в слово в query.lower().split(), если слово не в стоп-словах]
бм25 = бм25()
bm25.fit(тексты)
баллы = bm25.search(запрос)
для оценки, документ в почтовом индексе (оценки, корпус):
счет = раунд (счет, 3)
print(str(оценка) + '\t' + документ)
query = 'Пересечение графа опроса и деревьев'
query = [слово в слово в query.lower().split(), если слово не в стоп-словах]
бм25 = бм25()
bm25.fit(тексты)
баллы = bm25.search(запрос)
для оценки, документ в почтовом индексе (оценки, корпус):
счет = раунд (счет, 3)
print(str(оценка) + '\t' + документ)
 . То есть найти более релевантный документ, отсортировать их в порядке убывания и представить пользователю. Кроме того, здесь мы вычисляем баллы для каждого документа, это становится дорогостоящим в вычислительном отношении, когда мы начинаем иметь большой размер корпуса. Таким образом, поисковая система использует инвертировал индекс , чтобы ускорить процесс. Инвертированный индекс состоит из списка всех уникальных слов, встречающихся в каком-либо документе, а для каждого слова — списка документов, в которых оно встречается, это позволяет нам быстро находить документы, содержащие термин в нашем запросе, и только затем мы вычисляем показатель релевантности для этого меньшего набора отзывов. Эта ссылка содержит хорошее описание этой концепции на высоком уровне.
. То есть найти более релевантный документ, отсортировать их в порядке убывания и представить пользователю. Кроме того, здесь мы вычисляем баллы для каждого документа, это становится дорогостоящим в вычислительном отношении, когда мы начинаем иметь большой размер корпуса. Таким образом, поисковая система использует инвертировал индекс , чтобы ускорить процесс. Инвертированный индекс состоит из списка всех уникальных слов, встречающихся в каком-либо документе, а для каждого слова — списка документов, в которых оно встречается, это позволяет нам быстро находить документы, содержащие термин в нашем запросе, и только затем мы вычисляем показатель релевантности для этого меньшего набора отзывов. Эта ссылка содержит хорошее описание этой концепции на высоком уровне.
 elastic.co/guide/en/elasticsearch/reference/current/analysis.html
'отображения': {
# этот ключ является "типом", который будет объяснен в следующем фрагменте кода
'_doc': {
'характеристики': {
'заглавие': {
'тип': 'текст',
'анализатор': 'английский'
}
}
}
}
}
заголовки = {'Тип контента': 'приложение/json'}
ответ = запросы.пут('http://localhost:9200/experiment', data=json.dumps(настройки), заголовки=заголовки)
отклик
elastic.co/guide/en/elasticsearch/reference/current/analysis.html
'отображения': {
# этот ключ является "типом", который будет объяснен в следующем фрагменте кода
'_doc': {
'характеристики': {
'заглавие': {
'тип': 'текст',
'анализатор': 'английский'
}
}
}
}
}
заголовки = {'Тип контента': 'приложение/json'}
ответ = запросы.пут('http://localhost:9200/experiment', data=json.dumps(настройки), заголовки=заголовки)
отклик
 elastic.co/guide/en/elasticsearch/reference/current/removal-of-types.html
URL-адрес = 'http://локальный:9200/эксперимент/_doc'
для документа в корпусе:
# вставляем документ в поле title
данные = {'название': документ}
ответ = запросы. сообщение (url, данные = json.dumps (данные), заголовки = заголовки)
отклик
elastic.co/guide/en/elasticsearch/reference/current/removal-of-types.html
URL-адрес = 'http://локальный:9200/эксперимент/_doc'
для документа в корпусе:
# вставляем документ в поле title
данные = {'название': документ}
ответ = запросы. сообщение (url, данные = json.dumps (данные), заголовки = заголовки)
отклик
