Формулы сокращённого умножения. Неполный квадрат суммы и разности
- Разложение формул сокращенного умножения
- Неполный квадрат суммы
- Неполный квадрат разности
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
a2 + b2 = (a + b)2 — 2ab — сумма квадратов;
a2 — b2 = (a + b)(a — b) — разность квадратов;
(a + b)2 = a2 + 2ab + b2 — квадрат суммы;
(a — b)2 = a
a3 + b3 = (a + b)(a2 — ab + b2) — сумма кубов;
a3 — b3 = (a — b)(a2 + ab + b2) — разность кубов;
(a + b)3 = a3 + 3a2b + 3ab2 + b3 — куб суммы;
(a — b)3 = a3 — 3a2b + 3ab2 — b3 — куб разности.
Обратите внимание, что a
и b
в формулах сокращённого умножения могут быть как числами, так и выражениями.
Разложение формул сокращенного умножения
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.
Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
a2 + b2 = (a + b)2 — 2ab.
Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)2 — 2ab = (a + b)(a + b) — 2ab = a2 + ab + ab + b2 — 2ab = a2 + b2.
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
a2 — b2 = (a + b)(a — b).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2.
Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:
(a — b)2 = a2 — 2ab + b2.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.
Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
a3 + b3 = (a + b)(a2 — ab + b2).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a2 — ab + b2) = a3 — a2b + ab2 + a2b — ab2 + b3 = a3 + b3.
Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
a3 — b3 = (a — b)(a2 + ab + b2).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3.
Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:
(a — b)3 = a3 — 3a2b + 3ab2 — b3.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) = a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3.
Неполный квадрат суммы
Выражение:
a2 + 2ab + b2
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
a2 + ab + b2,
которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
Выражение:
a2 — 2ab + b2
это квадрат разности, который также называется полным квадратом разности относительно выражения:
a2 — ab + b2,
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Обзор формул
Если вы не знакомы с Excel в Интернете, скоро вы обнаружите, что это не просто сетка, в которую вы вводите числа в столбцах или строках. Да, можно использовать Excel в Интернете для поиска итогов по столбцу или строке чисел, но можно также вычислить платеж по кредиту, решить математические или технические задачи или найти оптимальный сценарий на основе переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)
Ниже приведены примеры формул, которые можно использовать на листах.
-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
- org/ListItem»>
=СЕГОДНЯ() Возвращает текущую дату.
-
=ПРОПИСН(«привет») Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.
-
=ЕСЛИ(A1>0) Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.
Элементы формулы
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
1. Функции. Функция ПИ() возвращает значение числа Пи: 3,142…
2. Ссылки. A2 возвращает значение ячейки A2.
3. Константы.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
|
Арифметический оператор |
Значение |
Пример |
|
+ (знак «плюс») |
Сложение |
3+3 |
|
– (знак «минус») |
Вычитание |
3–1 |
|
* (звездочка) |
Умножение |
3*3 |
|
/ (косая черта) |
Деление |
3/3 |
|
% (знак процента) |
Доля |
20% |
|
^ (крышка) |
Возведение в степень |
3^2 |
Операторы сравнения
Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
|
Оператор сравнения |
Значение |
Пример |
|
= (знак равенства) |
Равно |
A1=B1 |
|
> (знак «больше») |
Больше |
A1>B1 |
|
< (знак «меньше») |
Меньше |
A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
A1<=B1 |
|
<> (знак «не равно») |
Не равно |
A1<>B1 |
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
|
Текстовый оператор |
Значение |
Пример |
|
& (амперсанд) |
Соединение или объединение последовательностей знаков в одну последовательность |
Выражение «Северный»&«ветер» дает результат «Северный ветер». |
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
|
Оператор ссылки |
Значение |
Пример |
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
B5:B15 |
|
; (точка с запятой) |
Оператор объединения. Объединяет несколько ссылок в одну ссылку. |
СУММ(B5:B15,D5:D15) |
|
(пробел) |
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов. |
B7:D7 C6:C8 |
Порядок выполнения Excel в Интернете в формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равенства (=). Excel в Интернете интерпретирует символы, которые следуют знаку равенства, как формулу. После знака равенства вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделяются операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если объединить несколько операторов в одну формулу, Excel в Интернете выполняет операции в порядке, показанном в следующей таблице. Если формула содержит операторы с одинаковым приоритетом (например, если формула содержит оператор умножения и деления), Excel в Интернете вычисляет операторы слева направо.
|
Оператор |
Описание |
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и — |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, приведенная ниже формула возвращает значение 11, так как Excel в Интернете выполняет умножение перед добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
Например, приведенная ниже формула возвращает значение 11, так как Excel в Интернете выполняет умножение перед добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
=5+2*3
В отличие от этого, если для изменения синтаксиса используются круглые скобки, Excel в Интернете 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, которые заключают первую часть формулы, принудительно Excel в Интернете сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающая скобка, аргументы функции, разделенные запятыми, и закрывающая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После ввода знака = (знак равенства) и начальных букв или триггера отображения Excel в Интернете под ячейкой отображается динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если это не так, Excel в Интернете отображает #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Использование ссылок в формулах
Ссылка определяет ячейку или диапазон ячеек на листе и сообщает Excel в Интернете где искать значения или данные, которые нужно использовать в формуле. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется ссылочный стиль A1, который ссылается на столбцы с буквами (A–XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
|
Ячейка или диапазон |
Использование |
|
Ячейка на пересечении столбца A и строки 10 |
A10 |
|
Диапазон ячеек: столбец А, строки 10-20. |
A10:A20 |
|
Диапазон ячеек: строка 15, столбцы B-E |
B15:E15 |
|
Все ячейки в строке 5 |
5:5 |
|
Все ячейки в строках с 5 по 10 |
5:10 |
|
Все ячейки в столбце H |
H:H |
|
Все ячейки в столбцах с H по J |
H:J |
|
Диапазон ячеек: столбцы А-E, строки 10-20 |
A10:E20 |
<c0>Ссылка на другой лист</c0>. В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
Относительные ссылки . Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
Абсолютные ссылки . Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
Смешанные ссылки . Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку имеет вид A$1, B$1 и т. д. Если положение ячейки с формулой изменяется, относительная ссылка меняется, а абсолютная — нет. При копировании или заполнении формулы по строкам и столбцам относительная ссылка автоматически изменяется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в ячейку B3 она автоматически изменяется с =A$1 на =B$1.
При копировании или заполнении формулы по строкам и столбцам относительная ссылка автоматически изменяется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в ячейку B3 она автоматически изменяется с =A$1 на =B$1.
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов . Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все листы, хранящиеся между начальным и конечным именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.
- org/ListItem»>
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
-
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
Что происходит при перемещении, копировании, вставке или удалении листов . Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование . Если вставить или скопировать листы между листами 2 и 6 (в этом примере это конечные точки), Excel в Интернете содержит все значения в ячейках A2–A5 из добавленных листов в вычислениях.
-
Удаление . При удалении листов между листами 2 и 6 Excel в Интернете удаляет их значения из вычисления.
-
Перемещение .
 При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления.
При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления. -
Перемещение конечного листа . При перемещении листа 2 или листа 6 в другое место в той же книге Excel в Интернете корректирует вычисление в соответствии с новым диапазоном листов между ними.
-
Удаление конечного листа . При удалении sheet2 или Sheet6 Excel в Интернете корректирует вычисление в соответствии с диапазоном листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки с «R», за которым следует номер строки и «C», за которым следует номер столбца.
Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки с «R», за которым следует номер строки и «C», за которым следует номер столбца.
|
Ссылка |
Значение |
|
R[-2]C |
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце |
|
R[2]C[2] |
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее |
|
R2C2 |
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца |
|
R[-1] |
Относительная ссылка на строку, расположенную выше текущей ячейки |
|
R |
Абсолютная ссылка на текущую строку |
При записи макроса Excel в Интернете некоторые команды с помощью ссылочного стиля R1C1. Например, если вы записываете команду, например нажатие кнопки « Автосчет», чтобы вставить формулу, которая добавляет диапазон ячеек, Excel в Интернете формулу с помощью стиля R1C1, а не стиля A1, ссылок.
Например, если вы записываете команду, например нажатие кнопки « Автосчет», чтобы вставить формулу, которая добавляет диапазон ячеек, Excel в Интернете формулу с помощью стиля R1C1, а не стиля A1, ссылок.
Использование имен в формулах
Можно создать определенные имена для представления ячеек, диапазонов ячеек, формул, констант или Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
|
Тип примера |
Пример использования диапазонов вместо имен |
Пример с использованием имен |
|
Ссылка |
=СУММ(A16:A20) |
=СУММ(Продажи) |
|
Константа |
=ПРОИЗВЕД(A12,9. |
=ПРОИЗВЕД(Цена,НСП) |
|
Формула |
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),»дд.мм.гггг») |
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),»дд.мм.гггг») |
|
Таблица |
A22:B25 |
=ПРОИЗВЕД(Price,Table1[@Tax Rate]) |
Типы имен
Существует несколько типов имен, которые можно создавать и использовать.
Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме того, Excel в Интернете иногда создает определенное имя, например при настройке области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая представляет собой коллекцию данных об определенной теме, которая хранится в записях (строках) и полях (столбцах). Excel в Интернете создает имя таблицы Excel в Интернете «Table1», «Table2» и т. д. при каждой вставке таблицы Excel в Интернете, но вы можете изменить эти имена, чтобы сделать их более значимыми.
Создание и ввод имен
Имя создается с помощью команды «Создать имя» из выделенного фрагмента. Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.
Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
-
Ввода Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>. Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.

-
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.
Тест на определение уровня B2. Узнай свой уровень! 🤓
Уровень B2 в Общеевропейских компетенциях владения иностранным языком (CEFR) представляет собой уровень владения английским языком upper-intermediate. На этом уровне вы должны понимать основные идеи сложных текстов, спонтанно и без проблем взаимодействовать с носителями английского языка и уметь создавать подробные тексты на различные темы.
Лорд Кельвин, известный физик и математик XIX века, сказал, что все, что можно измерить, можно улучшить. В ABA English мы хотим помочь вам на пути к овладению английским языком. Очень важно знать о своем уровне и прогрессе. С нашим тестом по английскому языку на определение уровня B2 вы узнаете свою отправную точку и сможете ставить цели. Мы всегда будем рядом с вами, чтобы вы могли и дальше учиться. Мы познакомим вас с нашим специальным методом, который поможет вам в этом.
Очень важно знать о своем уровне и прогрессе. С нашим тестом по английскому языку на определение уровня B2 вы узнаете свою отправную точку и сможете ставить цели. Мы всегда будем рядом с вами, чтобы вы могли и дальше учиться. Мы познакомим вас с нашим специальным методом, который поможет вам в этом.
Что такое тест по английскому на определение уровня B2?
Вы являетесь хозяином своего учебного процесса, поэтому вы должны определить свои цели и стратегию их достижения. Этот процесс включает частую оценку ваших знаний. Доказательство вашего прогресса покажет вам, что вы делаете двигаетесь в нужном направлении, и поможет вам сохранить мотивацию.
Бесплатный тест на уровень B2 – это имитация официального сертификационного экзамена. Для чего он нужен?
ABA English разработала для вас бесплатный онлайн-тест по английскому языку на определение уровня B2, который состоит из нескольких вопросов. Вы можете пройти тест с компьютера, планшета или смартфона всего за несколько минут. Мы разработали тест на основе конкретных областей грамматики и знаний словарного запаса соответствующих уровню B2, чтобы мы могли точно оценить ваш уровень.
Мы разработали тест на основе конкретных областей грамматики и знаний словарного запаса соответствующих уровню B2, чтобы мы могли точно оценить ваш уровень.
Как узнать, готов ли я к тесту по английскому на определение уровня B2?
Мы хотим, чтобы вы рассматривали онлайн-тест на уровень B2 по английскому языку как часть процесса обучения, а не как самоцель. Не стоит бояться теста, поскольку это всего лишь предварительный диагноз. Но чтобы вы чувствовали себя увереннее, убедитесь, что вы освоили следующие темы.
4 навыка- Чтение: Убедитесь, что вы понимаете смысл и основные идеи статей, авторских колонок и литературных текстов.
- Аудирование: Вы должны понимать сюжет фильмов, радиошоу, беседы и конференции как на общие, так и на специальные темы.
- Письмо: Практикуйтесь в написании сложных, структурированных и организованных текстов. Цель этого не только в том, чтобы вас поняли, но и в правильном использовании языка.

- Разговорная речь: Вы должны уметь выражать свои мысли достаточно бегло, чтобы поддерживать разговор с носителем языка.
Вы должны знать все времена глаголов и знать, как правильно их спрягать. Используйте модальные глаголы, чтобы рекомендовать, запрещать и т. д. Используйте условные выражения правильно. Вам также необходимо знать косвенную речь и пассивный залог.
Словарный запасНа веб-сайте Кембриджа вы найдете список лексики для этого уровня. Этот список – хорошая отправная точка, но он не охватывает весь словарный запас, который вам следует знать. Вам также следует знать словосочетания, которые при совместном использовании имеют определенное значение.
Пройдите тест по английскому языку и проверьте свой уровеньНАЧАТЬ ТЕСТ
Советы по сдаче теста на определение уровня B2 по английскому языку
Хорошо подготовьтесьВ Интернете полно информации о различных темах, рассматриваемых на каждом уровне CEFR. Прежде чем сдавать тест B2 по английскому языку, изучите и просмотрите темы, которые, по вашему мнению, вам необходимо улучшить. Возможно, вы забыли некоторые из них из-за того, что не использовали их.
Прежде чем сдавать тест B2 по английскому языку, изучите и просмотрите темы, которые, по вашему мнению, вам необходимо улучшить. Возможно, вы забыли некоторые из них из-за того, что не использовали их.
Это не официальный тест, но он может дать вам ценную информацию о ваших сильных и слабых сторонах. Внимательно прочтите каждый вопрос и изучите возможные ответы. Помните, что эти тесты упрощены для вашего удобства. Сконцентрируйтесь, потому что вы обнаружите, что ответы очень похожи (специально), и вы даже можете почувствовать, что имеется более одного правильного варианта.
Проведите небольшое исследование перед выборомУ вас будут сотни вариантов тестов, некоторые для академических целей, а другие – для коммерческих. Изучите каждый из них, чтобы не проходить тест, который не даст вам надежного результата. Вы можете попробовать наш бесплатный тест по английскому языку на уровень B2 онлайн – он основан на академическом опыте, который предлагает ABA English.
ABA English поможет вам при прохождении этого теста, а также любых будущих.
Ваш тест по английскому языку на определение уровня B2 – это просто срез ваших знаний на момент его сдачи. Ваша глобальная цель – улучшить свой английский. В этом вы также можете рассчитывать на нас. Вот лишь некоторые из наших преимуществ.
Метод Smart Learning®
Мы хотим, чтобы вы получали удовольствие во время обучения. Вот почему наш метод Smart Learning® основан на том факте, что мозг лучше всего реагирует на благоприятные стимулы. Это означает, что если вам что-то нравится, ваш разум классифицирует это как важное и легче усваивает.
Учебные планы
У нас есть сертифицированный курс из 144 блоков, который охватывает все темы, входящие в шесть уровней CEFR, от A1 до Business. Он также соответствует требованиям к сертификации самых престижных учебных заведений. Но это не все! В дополнение к курсу у нас есть индивидуальный ежедневный план для вас с занятиями, которые вы можете практиковать ежедневно.
Наши ресурсы
С нашим приложением вы можете наслаждаться всеми нашими материалами и учиться где угодно и когда угодно. Мы постоянно создаем и обновляем наш контент, чтобы вы всегда могли учиться на том, что вам нравится. У вас будет доступ к микроурокам, разговорным сессиям, подкастам, статьям и многим другим ресурсам, чтобы вы никогда не пропустили практическое занятие.
Вы готовы к тесту?
Если вы хотите узнать, какой у вас уровень, наш тест доступен и займет всего несколько минут. Готовы начать?
Будьте готовы сдать любой тест с ABA English2 Формула?Формула a 2 — b 2 задается как: a 2 — b 2 = (a — b) (a + b)
умножьте (a — b) (a + b) и посмотрите, получится ли 2 — b 2 .
Проверка a
2 — b 2 Формула Давайте посмотрим на доказательство формулы квадрат минус b квадрат. Чтобы убедиться, что a 2 — b 2 = (a — b) (a + b), нам нужно доказать, что LHS = RHS. Попробуем решить уравнение:
Чтобы убедиться, что a 2 — b 2 = (a — b) (a + b), нам нужно доказать, что LHS = RHS. Попробуем решить уравнение:
а 2 — б 2 = (а — б) (а + б)
Умножаем (a — b) и (a + b) получаем
=а(а+б) -б(а+б)
=а 2 + аб — ба — б 2
=а 2 + 0 + б 2
=а 2 — б 2
Следовательно, проверено
a 2 — b 2 = (a — b) (a + b)
Вы можете понять формулу a 2 — b 2 геометрически, используя следующий рисунок: 92 Формула
Доказательство того, что значение a 2 — b 2 равно (a + b)(a — b). Рассмотрим приведенный выше рисунок. Возьмите два квадрата со сторонами a единиц и b единиц соответственно. Это также может быть представлено как сумма площадей двух прямоугольников, как показано на рисунке ниже.
Один прямоугольник имеет длину в единицу и ширину в (a – b) единиц, с другой стороны второй прямоугольник имеет длину в (a – b) и ширину в b единиц. Теперь сложите площади двух прямоугольников, чтобы получить результирующие значения. Соответствующие площади двух прямоугольников равны (a – b) × a = a(a – b) и (a – b) × b = b(a – b). Сумма площадей прямоугольников представляет собой фактическое полученное результирующее выражение, т. е. a(a + b) + b(a — b) = (a + b)(a — b). Снова переставляя отдельные прямоугольники и квадраты, мы получаем: (a+b)(a−b)=a 92 формула.
Теперь сложите площади двух прямоугольников, чтобы получить результирующие значения. Соответствующие площади двух прямоугольников равны (a – b) × a = a(a – b) и (a – b) × b = b(a – b). Сумма площадей прямоугольников представляет собой фактическое полученное результирующее выражение, т. е. a(a + b) + b(a — b) = (a + b)(a — b). Снова переставляя отдельные прямоугольники и квадраты, мы получаем: (a+b)(a−b)=a 92 формула.
Пример 1: Используя формулу 2 — b 2 , найдите значение 106 2 — 6 2 .
Решение: Чтобы найти: 100 2 — 6 2 .
Предположим, что a = 100 и b = 6.
Мы заменим их в формуле a 2 — b 2 .
а 2 — б 2 = (а — б) (а + б)
106 2 — 6 2 = (106 — 6) (106 + 6)
= (100) (112)
= 11200
Ответ: 106 2 — 6 2 = 11200.
Пример 2: Фактор. — 64.
Мы будем использовать формулу a 2 — b 2 , чтобы разложить это на множители.
Мы можем записать данное выражение как
25x 2 — 64 = (5x) 2 — 8 2
Подставим a = 5x и b = 8 в формулу a 2 — b 2 .
а 2 — б 2 = (а — б) (а + б)
: Упрощение 10 2 — 5 2 с использованием a 2 — b 2 формула
92 Формула
Что такое расширение формулы
2 — b 2 ?a 2 — b 2 формула читается как квадрат минус b квадрат. Его разложение выражается как а 2 — b 2 = (a — b) (a + b)
Что такое а
2 — b 2 Формула в алгебре? Формула a 2 — b 2 также известна как одна из важных алгебраических тождеств. Это читается как квадрат минус b квадрат. это 2 — b 2 формула выражается как a 2 — b 2 = (a — b) (a + b)
Это читается как квадрат минус b квадрат. это 2 — b 2 формула выражается как a 2 — b 2 = (a — b) (a + b)
Давайте разберемся в использовании формулы a 2 — b 2 на следующем примере.
Пример: Найдите значение 10 2 — 2 2 , используя формулу a 2 — b 2 .
Найти: 10 2 — 2 2
Предположим, что a = 10 и b = 2,
Мы подставим их в формулу a 2 — b 2 .
а 2 — б 2 = (а — б) (а + б)
10 2 -2 2 = (10-2)(10 + 2)
= 10 (10 + 2) — 2 (10 + 2)
= 10(12) — 2(12)
=120 — 24 = 96
Ответ: 10 2 — 2 2 = 96.
Как использовать a
2 92 формула может быть выражена как:a 2 + b 2 = (a +b) 2 — 2ab
Кроме того, + 2ab
где, a, b = произвольные числа.
Пусть a и b — два числа, квадраты a и b равны a 2 и b 2 . Сумма квадратов a и b равна a 2 + b 2 . Мы могли бы получить формулу, используя известное алгебраическое тождество (a+b) 92 Формула
Пример 1: Используя формулу суммы квадратов, найдите значение 5 2 + 6 2 ?
Решение:
Чтобы найти: значение 5 2 + 6 2
Дано: а = 5, б = 6
Используя формулу суммы квадратов,
а 2 + б 2 = (а + б) 2 — 2аб
5 2 + 6 2 = (5 + 6) 2 − 2(5)(6)
= 121 — 2(30)
= 121 − 60
= 61
Ответ: значение 5 2 + 6 2 IS 61.
Пример 2: Убедитесь, что значение x 2 + y 2 IS (x + y) 2 — 2xy по формуле 2 + b 2 .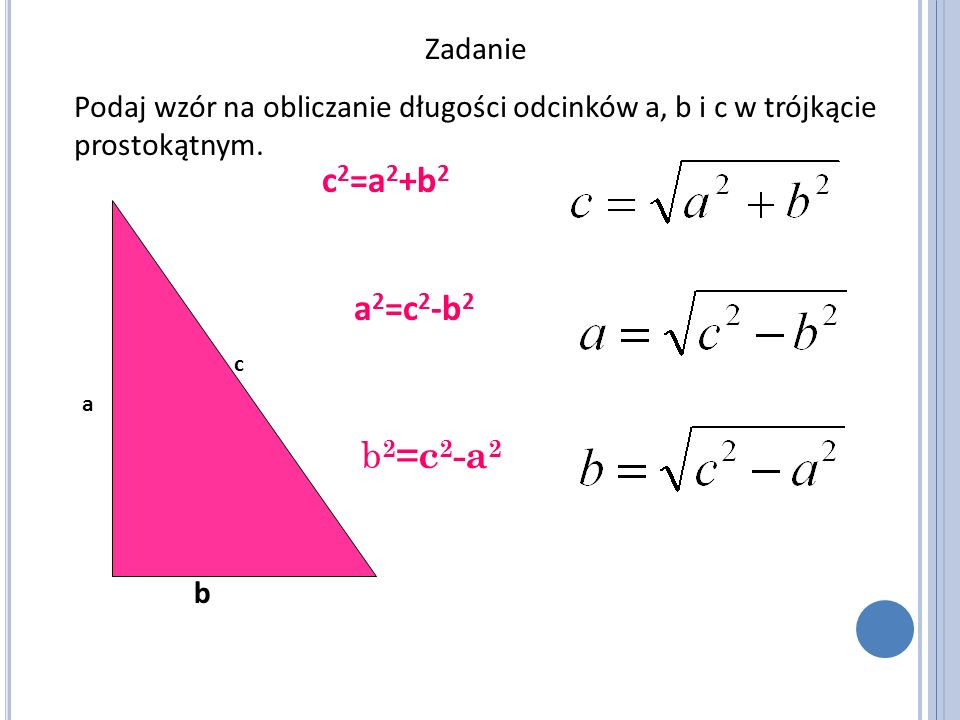
Решение: Для проверки x 2 + y 2 = (x + y) 2 — 2xy
Воспользуемся формулой a 2 + b 2
.а = х, б = у
По формуле (a + b) 2 разложим исходные члены.
(а + б) 2 = а 2 + б 2 + 2аб
Подставим значения a и b вместо x и y
(x + y) 2 = x 2 + y 2 + 2xy
Вычитая 2xy с обеих сторон,
x 2 + y 2 = (x + y) 2 — 2xy
Ответ: Следовательно, проверено 92 формула. Подтвердите свои ответы.
Решение:
10 2 + 20 2 = 100 + 400 = 500
Используя формулу а 2 + b 2 = (a +b) 2 -2ab, получаем 10 2 + 20 2 = (10 + 20 × 2 2
)
= 900 — 400
= 500
Таким образом проверено.
Часто задаваемые вопросы о
2 + b 2 ФормулаЧто такое расширение
2 + b 2 Формула?a 2 + b 2 формула известна как формула суммы квадратов, она читается как квадрат плюс b квадрат. Его расширение выражается как а 2 + b 2 = (a + b) 2 -2ab.
Что такое a
2 + b 2 Формула в алгебре?Формула a 2 + b 2 является одним из важных алгебраических тождеств. Он представлен a 2 + b 2 и читается как квадрат плюс b квадрат. Формула (a 2 + b 2 ) выражается как a 2 + b 2 = (a +b) 2 -2ab.
Как упростить числа, используя формулу a
2 + b 2 ? Давайте разберемся в использовании формулы a 2 + b 2 a 2 + b 2 на следующем примере.
Пример: Найти значение 20 2 + 30 2 по формуле a 2 + b 2 .
Чтобы найти: 20 2 + 30 2
Предположим, что a = 20 и b = 30,
Мы подставим их в формулу суммы квадратов, то есть a 2 + b 2
а 2 + б 2 = (а +б) 2 -2аб
20 2 +30 2 = (20+30) 2 — 2(20)(30)
= 2500 — 1200 = 1300 92 как власть или нет и в виде 2 + б 2 .
Завершение квадрата
» Завершение квадрата » вот где мы…
| … возьмем квадратное уравнение вот так: | и превратите его в это: | |
| ах 2 + Ьх + с = 0 | а(х+ d ) 2 + е = 0 |
Для тех из вас, кто торопится, могу сказать, что: d = b 2a
и: e = c − b 2 4a
Но если у вас есть время, позвольте мне показать вам, как » Заполнить квадрат » самостоятельно.
Завершение квадрата
Скажем, у нас есть простое выражение вида x 2 + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?
Что ж, немного вдохновившись геометрией, мы можем преобразовать его вот так:
Как видите x 2 + bx можно переставить почти в квадрат…
… и мы можем завершить квадрат с помощью (b/2) 2
В алгебре это выглядит так:
| x 2 + шт | + (б/2) 2 | = | (х+b/2) 2 |
| «Завершить квадрат » 907:45 |
Итак, сложив (b/2) 2 , мы можем завершить квадрат.
Результат (x+b/2) 2 имеет x только один раз , что проще в использовании.
Сохранение равновесия
Теперь… мы не можем просто прибавить (b/2) 2 без вычитания ! В противном случае меняется все значение.
Итак, давайте посмотрим, как это сделать правильно на примере:
| Начните с: | |
| («b» в данном случае равно 6) | |
| Заполните квадрат: | |
| Также вычесть новый член |
Упростите это, и все готово. | |
Результат:
x 2 + 6x + 7 = (x+3) 2 − 2
И теперь x появляется только один раз, и наша работа выполнена!
Быстрый подход
Вот быстрый способ получить ответ. Вам может понравиться этот метод.
Вам может понравиться этот метод.
Сначала подумайте о желаемом результате: (x+d) 2 + e
После расширения (x+d) 2 получаем: x 2 + 2dx + d 2 + e
Теперь посмотрим, сможем ли мы преобразовать наш пример в эту форму, чтобы обнаружить d и e
Пример: попробуйте вписать x
2 + 6x + 7 в x 2 + 2dx + d 2 + eТеперь мы можем «форсировать» ответ:
- Мы знаем, что
- мы должны закончить как 2dx, так что д должен быть 3
- Далее мы видим, что 7 должно стать d 2 + e = 9 + e, поэтому e должно быть −2
И мы получаем тот же результат (x+3) 2 − 2, что и выше!
Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений…
Решение общих квадратных уравнений путем заполнения квадрата
Мы можем дополнить квадрат до решить Квадратное уравнение (найти, где оно равно нулю).

Но общее квадратное уравнение может иметь коэффициент а перед х 2 :
топор 2 + Ьх + с = 0
Но с этим легко справиться… просто сначала разделите все уравнение на «а», а затем продолжайте:
х 2 + (б/а)х + с/а = 0
шагов
Теперь мы можем решить квадратное уравнение за 5 шагов:
- Шаг 1 Разделите все члены на a (коэффициент x 2 ).
- Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
- Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.
Теперь у нас есть что-то похожее на (x + p) 2 = q, которое довольно просто решается:
- Шаг 4 Извлеките квадратный корень из обеих частей уравнения.

- Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .
Примеры
Хорошо, несколько примеров помогут!
Пример 1: Решить x
2 + 4x + 1 = 0Шаг 1 можно пропустить в этом примере, так как коэффициент x равен 2 равно 1
Шаг 2 Перенесите числовой член в правую часть уравнения:
x 2 + 4x = -1
Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте это, добавив такое же число в правую часть уравнения.
(b/2) 2 = (4/2) 2 = 2 2 = 4 = 3
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
x + 2 = ±√3 = ±1,73 (до 2 знаков после запятой)
Шаг 5 Вычтите 2 из обеих частей:
x = ±1,73 – 2 = -3,73 или -0,27
А вот еще интересная и полезная штука.

В конце шага 3 у нас было уравнение:
(х + 2) 2 = 3
Это дает нам вершину (точка поворота) х 2 + 4х + 1: (-2, -3)
Шаг 1 правая часть уравнения:x 2 – 0,8x = 0,4
Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же число в правую часть уравнения:
(b/2) 2 = (0,8/2) 2 = 0,4 2 = 0,16
x 2 — 0,8x + 0,16 = 0,4 + 0,16
(x — 0,4) 2 = 0,56
Шаг 4 Примите квадратный корень на обеих сторонах. уравнение:
x – 0,4 = ±√0,56 = ±0,748 (до 3 знаков после запятой)
Шаг 5 Вычесть (-0,4) с обеих сторон (другими словами, добавить 0,4):
x = ±0,748 + 0,4 = -0,348 или 1,148
Почему «Завершить квадрат»?
Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу, чтобы решить квадратное уравнение?
Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.

Бывают также случаи, когда форма ax 2 + bx + c может быть частью большего вопроса , и перестановка его как a(x+ d ) 2 + e упрощает решение, потому что x появляется только один раз.
Например, «x» может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.
Также завершение квадрата является первым шагом в выводе квадратичной формулы
Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.
364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206
Сноска: значения «d» и «e»
Как я получил значения d и e из верхней части страницы?
Начните с Разделите уравнение на a Положите с на другую сторону Добавить (b/2a) 2 на обе стороны «Заполните квадрат» Теперь верни все обратно.  ..
..… на левую сторону … к исходному кратному a x 2 И вы заметите, что у нас есть:
а(х+d) 2 + е = 0 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92
Как доказать, что 1 = 2?
Быстро, сколько будет 1 + 1? Очевидно, 2, верно? Не так быстро!
Что, если бы я сказал вам, что могу доказать, что 1 + 1 на самом деле равно 1.
 И что, следовательно, 2 равно 1. Вы бы подумали, что я сошел с ума? Больше похоже на полное безумие? Вероятно. Но орехи или нет, это именно то, о чем мы будем говорить сегодня.
И что, следовательно, 2 равно 1. Вы бы подумали, что я сошел с ума? Больше похоже на полное безумие? Вероятно. Но орехи или нет, это именно то, о чем мы будем говорить сегодня.Конечно, здесь будет задействована хитрость, потому что 1 + 1, безусловно, равно 2… слава богу! И, как оказалось, этот трюк связан с очень интересным фактом о числе ноль.
Как это все работает? И что за большая уловка, которую пытается провернуть подлый номер ноль? Продолжайте читать, чтобы узнать!
Спонсор: Посетите GoDaddy.com, чтобы получить домен .COM за 2,95 доллара. Применяются некоторые ограничения, подробности см. на веб-сайте.
Как «доказать», что 2 = 1
Давайте начнем наше путешествие в причудливый мир внешне правильных, но явно абсурдных математических доказательств, убедив себя, что 1 + 1 = 1. И, следовательно, что 2 = 1. Я знаю это звучит безумно, но если вы будете следовать логике (и еще не знаете хитрости), я думаю, вы обнаружите, что «доказательство» довольно убедительно.

Вот как это работает:
- Предположим, что у нас есть две переменные a и b и что: a = b
- Умножьте обе части на и , чтобы получить: и 2 = ab
- Вычтем b 2 с обеих сторон, чтобы получить: a 2 – b 2 = ab – 9 70 2
- Это сложная часть: разложите на множители левую часть (используя FOIL из алгебры), чтобы получить ( a + b )( a – b ), и вычтите b из правой части, чтобы получить б ( а – б ). Если вы не знаете, как работает FOIL или факторинг, не волнуйтесь — вы можете проверить, что все это работает, перемножив все, чтобы убедиться, что оно совпадает. Конечным результатом является то, что наше уравнение стало таким: 90 108 ( а + б )( а – б ) = б ( а – б )
- Поскольку ( a – b ) появляется с обеих сторон, мы можем сократить его, чтобы получить: a + b = b
- Поскольку a = b (это предположение, с которого мы начали), мы можем заменить b на a , чтобы получить: b + b = б
- Объединение двух членов слева дает нам: 2 b = b
- Так как b появляется с обеих сторон, мы можем разделить на b , чтобы получить: 2 = 1
Подождите, что?! Все, что мы там делали, выглядело вполне разумно.
 Как же нам удалось доказать, что 2 = 1?
Как же нам удалось доказать, что 2 = 1?Что такое математические ошибки?
На самом деле мы не доказали, что 2 = 1. Что, к счастью, означает, что вы можете расслабиться — мы не разрушили все, что вы знаете и любите о математике. Где-то в этом «доказательстве» зарыта ошибка. На самом деле, «ошибка» — не то слово, потому что это была не ошибка в том, как мы выполняли арифметические действия, а гораздо более тонкая махинация, известная как «математическая ошибка».
Никогда нельзя делить на ноль!
В чем заключалась ошибка знаменитого фальшивого доказательства, которое мы рассматривали? Как и многие другие математические ошибки, наше доказательство основано на тонком трюке деления на ноль. И я говорю тонко, потому что это доказательство построено таким образом, что вы можете даже не заметить, что происходит деление на ноль. Где это происходит? Потратьте минутку и посмотрите, сможете ли вы это понять…
Хорошо, понял?
Это произошло, когда мы разделили обе части на a – b на пятом шаге.
 Но вы говорите, что это не деление на ноль — это деление на а — б . Это верно, но мы начали с предположения, что a равно b , а это значит, что a – b — это то же самое, что и ноль! И хотя вполне нормально делить обе части уравнения на одно и то же выражение, делать это неправильно, если выражение равно нулю. Потому что, как нас всегда учили, никогда нельзя делить на ноль!
Но вы говорите, что это не деление на ноль — это деление на а — б . Это верно, но мы начали с предположения, что a равно b , а это значит, что a – b — это то же самое, что и ноль! И хотя вполне нормально делить обе части уравнения на одно и то же выражение, делать это неправильно, если выражение равно нулю. Потому что, как нас всегда учили, никогда нельзя делить на ноль!Почему нельзя делить на ноль?
Вы можете задаться вопросом: почему именно мы не можем делить на ноль? Нас всех предупреждали о таких вещах с тех пор, как мы были маленькими мальчиками и девочками, но задумывались ли вы когда-нибудь о том, почему деление на ноль — это такой оскорбительный поступок? Есть много способов подумать об этом. Сегодня мы поговорим о двух причинах.
Первое связано с тем, как деление связано с умножением. Давайте на секунду представим, что деление на ноль — это прекрасно и модно. В этом случае задача наподобие 10/0 будет иметь некоторое значение, которое мы назовем 9.
 0758 х . Мы не знаем, что это такое, но просто предположим, что x — это какое-то число. Таким образом, 10/0 = x . Мы также можем рассматривать эту задачу деления как задачу умножения: какое число, x , нужно умножить на 0, чтобы получить 10? Конечно, на этот вопрос нет ответа, поскольку каждое число , умноженное на ноль, равно нулю. Это означает, что операция деления на ноль называется «неопределенной».
0758 х . Мы не знаем, что это такое, но просто предположим, что x — это какое-то число. Таким образом, 10/0 = x . Мы также можем рассматривать эту задачу деления как задачу умножения: какое число, x , нужно умножить на 0, чтобы получить 10? Конечно, на этот вопрос нет ответа, поскольку каждое число , умноженное на ноль, равно нулю. Это означает, что операция деления на ноль называется «неопределенной».Второй способ осмыслить несуразность деления на ноль и причину, по которой мы не можем этого сделать, — это представить себе деление числа вроде 1 на все меньшие и меньшие числа, которые все ближе и ближе к нулю. Например:
- 1 / 1 = 1
- 1/0,1 = 10
- 1/0,01 = 100
- 1/0,001 = 1000
- 1 / 0,0001 = 10 000
- …
- 1 / 0,00000000001 = 100 000 000 000
и так далее до бесконечности. Другими словами, когда мы делим 1 на все более мелкие числа, которые все ближе и ближе к нулю, мы получаем все больший и больший результат.
 В пределе, когда знаменатель этой дроби фактически становится нулем, результат был бы бесконечно большим.
В пределе, когда знаменатель этой дроби фактически становится нулем, результат был бы бесконечно большим.Это еще одна очень веская причина, по которой мы не можем делить на ноль. И почему 1 + 1 действительно равно 2… что бы ни говорило наше дурацкое «доказательство».
Подведение итогов
Хорошо, это все математические расчеты, на которые у нас есть время.
Обязательно ознакомьтесь с моей книгой «Краткое и грязное руководство по алгебре для чуваков-математиков» . И не забудьте стать поклонником Math Dude на Facebook , где вы найдете много отличных математических публикаций в течение недели. Если вы есть в Твиттере, подпишитесь на меня и там.
До свидания, это Джейсон Маршалл с Быстрые и грязные советы математика для упрощения математики . Спасибо за чтение, любители математики!
Изображения дополнений Apple и лампочки бесконечности от Shutterstock.
Графические уравнения и системы уравнений с помощью программы «Пошаговое решение математических задач»
ВВЕДЕНИЕ В КВАДРАТИКА
Цели
В этом разделе вы будете складывать, вычитать, умножать и строить графики квадратичных уравнений.

Словарь : Стандартный формат квадратного уравнения : y = ax 2 + bx + c ; а, b, с — константы; x — независимая переменная, y — зависимая переменная. Квадратичные числа также называются полиномами второй степени , потому что наивысший показатель степени равен 2. Уравнение пересечения наклона из второй главы y = mx + b называется полиномом первой степени , потому что старший показатель равен единице.
Зачем изучать квадратику? Графики квадратных уравнений представляют собой параболы (графики U-образной формы, открывающиеся вверх или вниз). Эта особенность квадратичных вычислений делает их хорошими моделями для описания пути объекта в воздухе или описания прибыли компании (примеры которых вы можете увидеть в конечной математике или в микроэкономике).
Пример 1. Мальчик лежит на Бэк использует выстрел из рогатки, чтобы выстрелить камнем прямо в воздух с начальной скоростью (сила, которую мальчик использует, чтобы выстрелить камнем) 64 фута в секунду.
 Квадратное уравнение, моделирующее высоту скалы, равно 9.0007
Квадратное уравнение, моделирующее высоту скалы, равно 9.0007ч = -16т 2 +64т.
а. Найдите высоту скалы при t = 0,
В формуле h = -16t 2 + 64t замените t на 0,
h = -16(0) 2 +64(0)
h = 0Камень находится в воздухе на ноль футов в ноль секунд. (Это момент прямо перед тем, как он выстрелит камнем в воздух.)
b. Найдите высоту скалы при t = 1,
В формуле h = -16t 2 + 64t замените t на 1,
В одну секунду камень находится в воздухе на высоте 48 футов.
Объяснение : Возводится в квадрат только «1». -16 умножается на 1 2
c. Найдите высоту скалы при t = 2,
В формуле h = -16t 2 + 64t замените t на 2,
Камень находится в воздухе на высоте 64 фута за 2 секунды.
Объяснение : Порядок операций требует применения показателей степени перед умножением.
д. Найдите высоту камня при t = 3,
В формуле h = -16t 2 + 64t замените t на 3,
Камень находится в воздухе на высоте 48 футов за 3 секунды.

эл. Найдите высоту скалы при t = 4.
В формуле h = -16t 2 +64t замените t на 4.
Камень находится в воздухе на ноль футов через 4 секунды; то есть камень ударился о землю.
ф. Нанесите на график точки, полученные в частях от a до e.
Высота скалы зависит от времени, поэтому h — зависимая переменная, t — независимая переменная. Точки имеют вид (t, h).
Согласно графику, камень достигает наибольшей высоты за 2 секунды. Максимальная высота составляет 64 фута. Максимальная или минимальная точка квадратного называется вершиной. Вы узнаете, как найти вершину, в Разделе 4.3, Квадратичные приложения и графы.
Согласно графику, камень находится на земле через ноль секунд (непосредственно перед тем, как мальчик выстрелит в него) и через 4 секунды (когда камень приземлится). Эти точки являются временными перехватами. Вы узнаете, как их найти, в следующем Разделе 4.2, «Применения квадратичной формулы».
Сложение и вычитание квадратичных чисел:
Словарь : Чтобы складывать или вычитать квадратичные числа, объединяйте одинаковые термины.
 Подобные термины , первоначально представленные в разделе 1.3 «Упрощение алгебраических выражений», имеют ту же переменную и тот же показатель степени. Например, 2x 2 и 5x 2 похожи, а 3x 2 и 7x — нет.
Подобные термины , первоначально представленные в разделе 1.3 «Упрощение алгебраических выражений», имеют ту же переменную и тот же показатель степени. Например, 2x 2 и 5x 2 похожи, а 3x 2 и 7x — нет.Коэффициент , первоначально представленный в Разделе 1.3 «Упрощение алгебраических выражений», представляет собой число, умножающее переменную. Например, коэффициент при 2x равен 2, а коэффициент при -x равен 9.0003 2 равно -1.
Правило: Чтобы объединить одинаковые термины, добавьте их коэффициенты
Напомним распределительное свойство : Определение a(b + c) = ab + ac.
Не удалось объединить непохожие термины внутри круглых скобок, поэтому мы использовали распределительное свойство. После этого мы умножили 6x на 3, а затем -5 на 3.
Использовали свойство распределения и комбинировали одинаковые термины.Пример 5. Уравнение прибыли: Прибыль = Доход — Затраты
Если уравнение доходов для компании:
, а уравнение затрат:
, найдите уравнение прибыли для компании.

Подставил уравнения выручки и затрат в формулу прибыли. Необходимо использовать скобки.
Использовал свойство распределения и умножил уравнение доходов на 1, а уравнение затрат на -1.
Комбинированные термины.Подставил уравнения выручки и затрат в формулу прибыли. Необходимо использовать скобки. Используется распределительное свойство. Умножил уравнение дохода на 1 и уравнение затрат на -1. Комбинированные подобные термины.
Умножение двух двучленов.
Словарь : Бином состоит из двух членов (так же, как велосипед имеет два колеса).
Правило: Чтобы умножить два двучлена, умножьте каждый член первого на каждый член второго.
Пример 7. Умножить (х + 2)(5х + 3).
Умножить x на 5x и 3 и умножить 2 на 5x и 3.
Объединить подобные термины.ФОЛЬГА — простая мнемоника, помогающая запомнить, как умножать два двучлена.
Пример 8. Умножить (8x + 6)(x + 7).

Учебный совет: Напишите карточку с объяснением мнемоники ФОЛЬГА. Чаще просматривайте карту.
Резюме
Квадратичные уравнения являются важными уравнениями в физике и микроэкономике. Техника сложения и вычитания квадратичных чисел та же самая, которую мы практиковали весь семестр; то есть добавить или вычесть подобные термины. Чтобы умножить, используйте распределительное свойство или FOIL. Вершина квадратичного уравнения будет объяснена более подробно в разделе «Квадратичные графики и приложения». Вершина — это максимальная или минимальная точка на графике квадратичного уравнения.
ПРИМЕНЕНИЕ КВАДРАТИЧНОЙ ФОРМУЛЫ
Цель
Этот раздел покажет вам, как решать квадратные уравнения.
Словарь : Квадратное уравнение равно ax 2 + bx + c = 0 . a, b и c — константы, а x — переменная.
Квадратная формула , , используется для решения квадратного уравнения.
Анализ
- a, b и c — числа, которые будут подставлены в формулу.

a — коэффициент квадрата переменной,
b — коэффициент переменной в первой степени,
c — константа. - Символ ± дает два решения уравнения.
Одно решение со знаком +, а другое решение со знаком -, . - — это символ квадратного корня.
- Потому что 4 2 = 16.
- Потому что 5.916 2 = 35.
- Ваш калькулятор необходим для этого раздела. Убедитесь, что вы можете найти кнопку на вашем калькуляторе.
- Вы можете вычислять квадратный корень только из неотрицательных чисел.
- Если вы попытаетесь вычислить, ваш калькулятор выдаст сообщение об ошибке.
Если вы изучите алгебру среднего уровня, вы узнаете о квадратных корнях из отрицательных чисел.
Учебный совет: Напишите квадратное уравнение и квадратную формулу на карточках, чтобы вы могли обращаться к ним, когда будете делать домашнюю работу.
Пример 1. Предположим, вы стоите на вершине утеса на высоте 375 футов над дном каньона и подбрасываете в воздух камень с начальной скоростью 82 фута в секунду.
 Уравнение, которое моделирует высоту скалы над дном каньона:
Уравнение, которое моделирует высоту скалы над дном каньона:h = -16t 2 + 82t + 375.
Найдите время, за которое камень упадет на дно каньона.
Найдите t при h = 0.
Решите 0 = -16t 2 +82t + 375.
Определите константы a, b и c.Объяснение : Одна сторона квадратного уравнения должна быть равна нулю.
a = -16, b = 82, c = 375
Пояснение :
a — коэффициент при переменной, возведенный в квадрат
b — коэффициент при переменной в первой степени.
с — константа.Используйте квадратичную формулу
с a = -16, b = 82 и c = 375. этаж, а время не может быть отрицательным.
T = 8,041 секунды — это время, за которое камень достигает дна каньона.
Камень упадет на дно каньона через 8,041 секунды.
Пример 2. Владелец ранчо имеет 500 ярдов забора, чтобы оградить два смежных загона для свиней, примыкающих к сараю. Если площадь двух загонов должна составлять 20 700 квадратных ярдов, то каковы должны быть размеры загонов?
L представляет собой длину обоих ручек.

а. Используя таблицу, найдите уравнение площади ручек.
б. Упростите уравнение площади.
в. Найдите W, если A = 20 700.
Ширина 76,67 или 90 ярдов.
д. Найдите длину ручек.
Из таблицы в Части а, L = 500 — 3W . Подставьте W = 76,67 и W = 90 в уравнение для длины, L = 500 — 3w.
Размеры свинарников площадью 20 700 квадратных ярдов: 76,67 на 270 ярдов и 90 на 230 ярдов.
Пример 3. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующую квадратичную модель можно смоделировать для температуры кислорода:
T = 0,26 м 2 -4,1 м + 7,9
, где Т измеряется в градусах Цельсия, а м представляет минуты, которые провел эксперимент. бегать. Определите, когда температура кислорода равна 0 градусов Цельсия.
Задача требует найти m при T = 0.
Температура кислорода будет равна 0 градусов Цельсия через 2,246 минуты и 13,52 минуты.

Совет по изучению: Ключевая идея, продемонстрированная в примере 3, заключается в том, как обращаться с отрицательным значением b в квадратном уравнении.
Резюме
В этом разделе показано, как решать новый тип уравнения, квадратное. Они имеют важные приложения во многих областях, таких как бизнес, физика и инженерия. Учиться разница между квадратным уравнением и квадратной формулой.
Квадратное уравнение: ax 2 + bx + c = 0.
- Одна часть уравнения должна быть равна нулю.
- а — коэффициент x .
- b — коэффициент при x.
- c — постоянный член.
Квадратная формула решает квадратное уравнение.
- Формула дает два решения.
- Калькулятор используется для поиска ответов.
- Первым шагом в оценке формулы является упрощение квадратного корня.
КВАДРАТИЧЕСКИЕ ПРИМЕНЕНИЯ И ГРАФЫ
Цели
В этом разделе исследуются дополнительные ключевые точки графа квадратичного уравнения, вершины и точки пересечения.
 Эти точки будут интерпретироваться в приложениях.
Эти точки будут интерпретироваться в приложениях.Пример 1. Лежащий на спине мальчик стреляет из пращи камнем прямо в воздух с начальной скоростью (сила, которую мальчик использует, чтобы выстрелить в камень) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно
9.0002 ч = -16т 2 + 64т.(Этот пример взят из Раздела 4.1 «Введение в квадратику», стр. 317.)
На странице 318 мы сгенерировали следующие значения:
Мы использовали точки для построения графика ниже. Вершина и пересечения также помечены на графике.
Объяснение : Точка (0, 0) является точкой пересечения и времени, и высоты.
Вершина , (2,64) представляет собой максимальную высоту скалы. Скала достигает максимальной высоты 64 фута за 2 секунды.
Отрезки времени , (0, 0) и (4, 0) представляют, когда камень находится на земле. Камень находится на земле за ноль секунд до выстрела (это перехват высоты ) и через 4 секунды, когда он возвращается на землю.

Чтобы построить квадрат, указанный уравнением, y = ax 2 + bx + c, освойте следующие термины:
Словарь : Вершина: Вершина — это максимальная или минимальная точка на графике. Чтобы найти вершину:
а. Найдите координату x:
б. Найдите координату y: подставьте значение x, полученное в части a, в формулу y = ax 2 + bx + c.Пересечение по оси X : Установите y = 0 и решите 0 = ax 2 + bx + c по формуле квадрата y всегда будет c, константой.
Учебный совет: Запишите процедуру и определения на трех карточках для удобства.
Пример 2. Компания D++ делает компьютерные игры. Стоимость создания g игр в месяц составляет C = 0,4g 2 — 32g + 625 . Доход от продажи g игр в месяц равен R = -0,6g 2 +52g. Единицы измерения g — сотни, а C и R — тысячи долларов.
а. Найдите уравнение прибыли.
б. Найдите вершину и объясните, что эта вершина означает с точки зрения создания компьютерных игр.

Формула для координаты g:
Из уравнения для прибыли a = -1, b = 84.
Вершина (42,1139). Если D+++ продаст 4 200 игр, то они получат максимальную прибыль в размере 1 139 000 долларов.
в. Найдите g и и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения g, установите P = 0.
Решите 0 = -g 2 + 84g — 625 .
Используйте квадратичную формулу, a = -1, b = 84, c = -625.
Отрезки g: (8.251, 0) и (75.75, 0).
Если они продадут 825 или 7575 игр, они окупятся.
д. Найдите P и и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения P, установите g = 0.
P = -0 2 +84*0-625
P = -625
Значение точки P равно (0, -625).
Начальные затраты компании составляют 625 000 долларов.эл. График функции.
Нанесите точки:
Вершина. (42, 1139).
(42, 1139).
Данные перехватывают. (8,251, 0) и (75,75, 0).
Перехват P. (0, -625).Объяснение : Одним из объяснений наличия двух точек безубыточности является то, насколько эффективно компания производит продукт. Изготовление очень небольшого количества предметов обычно неэффективно. В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много изделий, компания становится неэффективной в производстве своей продукции.
Помните, что единицы g измеряются сотнями, а единицы P — тысячами.
Предположим, что D+++ должен получать прибыль в размере 500 000 долларов (P = 500) в месяц. Нарисуйте эту линию на графике, полученном в части б, и найдите, где линия пересекает график квадратичного уравнения. Напишите предложение, объясняющее, что означают ответы.
Эскиз P = 500 на предыдущем графике.
P = 500 — горизонтальная линия.
Если D+++ хочет получить прибыль в размере 500 000 долларов, им нужно сделать и продать 1 672 или 6 728 игр.

Пояснение : На графике показано, где пересекаются горизонтальная линия P = 500 и уравнение прибыли P = -g 2 +84g-625. Алгебра дает точную точку, где они пересекаются.
г. Используя график и ответы к части c, определите, сколько компьютерных игр необходимо создать и продать, чтобы гарантировать прибыль более 500 000 долларов.
Компания получит прибыль более 500 000 долларов, если график прибыли окажется выше горизонтальной линии P = 500. Эта задача аналогична примеру 2d на странице 203 в разделе 2.9.«Применения графиков».
Это происходит между точками g = 16,72 и g = 67,28 или
16,72
Компания заработает более 500 000 долларов, когда создаст и продаст от 1 672 до 6 728 компьютерных игр.
Пример 3. Владелец питомника хочет пристроить к стене три соседних загона для собак одинакового размера. У него 96 метров забора.
а. Найдите формулу площади.
Объяснение : Самая трудная часть таблицы — найти значение длины.
 Если фермер использует 10 метров для ширины загонов, а их ширина 4, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений у него осталось по длине, из 9 вычтите 40.6, общее количество ограждений, доступных фермеру.
Если фермер использует 10 метров для ширины загонов, а их ширина 4, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений у него осталось по длине, из 9 вычтите 40.6, общее количество ограждений, доступных фермеру.Формула площади загонов для собак:
b. Найдите вершину и объясните, что она означает в терминах собачьих загонов.
Формула для координаты W:
Из уравнения для прибыли, a = -4, b = 96.
Вершина (12, 576).
Вершина , (12, 576) представляет максимальную площадь трех загонов для собак. Когда W = 12, максимальная площадь будет 576. (Длина всех трех загонов будет 48 или длина одного загона для собак будет 16.) Будет три загона для собак размером 12 на 16 метров.
с. Найдите W и и объясните, что они означают в терминах собачьих загонов.
Чтобы найти точку пересечения W, установите A = 0.
Решите 0 = -4W 2 + 96W.

Используйте квадратичную формулу, a = -4, b = 96, c = 0.
Пересечения W равны (0, 0) и (24, 0).
Отрезки W, (0, 0) и (24, 0) представляют собой ширину собачьих загонов, которые дадут нулевую площадь.
д. Найдите перехват A и объясните, что это означает применительно к загонам для собак.
Чтобы найти точку пересечения A, установите W = 0.
Объяснение : Если ширина прямоугольника равна нулю, то площадь должна быть равна нулю.
Точка пересечения (0, 0).
Точка пересечения A (0, 0) — это площадь, когда W = 0.
e. Нарисуйте уравнение
Нанесите точки:
Вершина. (12, 576).
W перехватывает. (0, 0) и (24, 0).
Перехват А. (0, 0).ф. Предположим, что общая площадь должна быть 400 квадратных метров. Постройте график A = 400 и найдите размеры загонов для собак.
Эскиз A = 400 на предыдущем графике.

A = 400 — горизонтальная линия.
Поскольку ширина W известна, длину L можно найти по формуле A = LW.
Найдите L, разделив обе части на W.
Размеры загонов для собак, которые дают площадь 400 квадратных метров, составляют 5,367 на 74,53 и 18,63 на 21,47.
Пример 4. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующую квадратичную модель можно смоделировать для температуры кислорода:
T = 0,26 м 2 -4,1 м + 7,9
, где Т измеряется в градусах Цельсия, а м представляет минуты, которые провел эксперимент. бегать. Постройте уравнение, найдя вершину и точки пересечения. Отметьте эти точки на графике и объясните, что означают вершины и точки пересечения с точки зрения модели.
Назад: Это та же самая модель, которая использовалась в примере 3 на стр. 332. Этот пример работал при нулевой температуре.
Найдите вершину T = 0,26 м 2 — 4,1 м + 7,9 .

Формула для m-координаты вершины: .
Вершина (7,885, -8,263).
Найдите м отрезков от T = 0,26 м 2 -4,1 м+ 7,9
Чтобы найти m отрезков, установите T = 0,
Решить 0 = 0,26 м 2 -4,1 м+ 7,9 .
Используйте квадратичную формулу, a = 0,26, b = -4,1, c = 7,9.
М точек пересечения (13,52, 0) и (2,246, 0).
Найдите точек пересечения T точки T = 0,26 м 2 — 4,1 м + 7,9
Чтобы найти точку пересечения T, установите m = 0,
(точка пересечения равна 7,
).
Вершина: Минимальная температура будет на 7.885 мин. Минимальная температура составит -8,263 градуса по Цельсию.
м пересечений: Температура будет равна нулю градусов Цельсия в 2.246 и 13.52 минуты.
Пересечение T: В начале эксперимента температура составляла 7,9 градусов Цельсия.
Учебные советы: Квадратичные графики представляют собой U-образные графики.
 В некоторых случаях они имеют U-образную форму, как в приведенном выше примере, или форму, как в примерах с 1 по 3. Если a в уравнении y = ax 2 + bx + c положительно, то график имеет U-образную форму, т. е. есть, открытие. Если a отрицательно, то график имеет форму, т. е. раскрывается вниз. Этот факт должен быть записан на карточке для заметок.
В некоторых случаях они имеют U-образную форму, как в приведенном выше примере, или форму, как в примерах с 1 по 3. Если a в уравнении y = ax 2 + bx + c положительно, то график имеет U-образную форму, т. е. есть, открытие. Если a отрицательно, то график имеет форму, т. е. раскрывается вниз. Этот факт должен быть записан на карточке для заметок.Резюме
Графики квадратичных уравнений появляются в таких разных предметах, как микроэкономика и физика. В этом разделе кратко излагаются основные идеи модуля.
Чтобы нарисовать квадрат, y = ax 2 + bx + c , вы должны найти:
- вершина .
Формула для координаты x:
Чтобы найти координату y, подставьте свой ответ вместо координаты x в уравнение y = ax 2 + bx + c . - x перехватывает .
Установите y = 0 и решите уравнение 0 = ax 2 + bx + c , используя квадратичную формулу
- y перехват .
Положим в уравнении x = 0, y = ax 2 + bx + c и найдем y. Обратите внимание, когда x = 0, y = c.
Обратите внимание, когда x = 0, y = c. - Если a отрицательное , то обычно график выглядит так:
- Если а положительное , то в целом график выглядит так:
ФАКТОРИЗАЦИЯ
Цели
Факторинг — это алгебраический метод, используемый для разделения выражения на составные части. Когда составные части перемножаются вместе, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг является важным навыком в MAT 100, Intermediate Algebra.
Словарь : Алгебраическое выражение факторизуется, если последней операцией при вычислении выражения является умножение.
Пример 1. Какое выражение представляет собой , разложенное на , х 2 — 5х — 24 или (х — 8)(х + 3)?
Выберите значение x и подставьте его в выражение.
Пусть x = 3.
Поскольку последней операцией для (x — 8)(x + 3) было умножение, то (x — 8)(x + 3) факторизуется.

Пояснение : Менее формально алгебраическое выражение факторизуется, если оно имеет круглые скобки.
Словарь : Распределительное свойство есть a(b + c) = ab + ac. Левая часть факторизуется, а является общим множителем.
Вы должны иметь возможность проверить, используя свойство дистрибутива.
Объяснение : Хотя 8x 3 + 4x равно как 2x(4x 2 + 2), так и 4(2x 3 + x), ни одно из них не считается полностью факторизованным, поскольку в обоих случаях общее кратное , 2, в 2х(4х 2 +2) и x в 4(2x 3 +x) все еще могут быть факторизованы из терминов в скобках.
Разложение трехчленов на множители: (Трехчлен состоит из трех членов.) Чтобы разложить трехчлен на множители, вспомните аббревиатуру FOIL.
Учебный совет: Проверьте свои карточки для заметок на предмет определения ФОЛЬГИ.
Пример 4. Умножить (x+3)(x+5).
(x+3)(x+5) учитывается, а x 2 + 8x +15 не учитывается.
 Чтобы разложить трехчлены, вам нужно знать, как были вычислены 8x и 15. 8х получилось от сложения 5х и 3х, а 15 получилось от умножения 5 и 3.
Чтобы разложить трехчлены, вам нужно знать, как были вычислены 8x и 15. 8х получилось от сложения 5х и 3х, а 15 получилось от умножения 5 и 3.Пример 5. Коэффициент х 2 + 8х +15. (Это из примера 4.)
Нам нужны два числа, которые при сложении равны 8, а при умножении равны 15. 3 и 5 в сумме дают 8, а при умножении 15.
Итак, x 2 + 8x +15 = (x + 3)(x + 5)
Пример 6. Фактор x 2 -4x- 12.
Нам нужны два числа, которые при сложении равны -4, а при умножении равны -12. -6 и 2 в сумме дают -4, а при умножении дают -12.
Так х 2 -4х -12 = (х-6)(х + 2).
Пример 7. Коэффициент x 2 — 64 .
Это не трехчлен, но он может стать им, если добавить 0x.
x 2 -64 = x 2 +0x -64
Нам нужны два числа, которые при сложении равны 0, а при умножении равны -64.
-8 и 8 прибавляются к 0 и при умножении дают -64.
Так х 2 -64 = (х-8)(х + 8).

Этот пример называется разложением на множители разности совершенных квадратов, и вы снова увидите его, если возьмете MAT 100, Средняя алгебра.
Словарь : a 2 — b 2 — это разность совершенных квадратов .
Разность полных квадратов имеет специальную формулу факторизации: a 2 — b 2 = (a — b)(a + b)Решение квадратных уравнений методом факторизации:
Если умножить две величины и результат равен нулю, то вы знаете, что одна из величин должна быть равна нулю. В математической записи
, если a.b = 0, то a = 0 или b = 0.
Прежде чем вы подумаете, что разложение на множители для решения квадратного уравнения намного проще, чем использование формулы квадратного уравнения, вы должны знать, что разложение на множители не всегда работает. Попробуйте изменить пример 8 всего на единицу до x 2 — 11x + 31 = 0. Вы не можете найти два целых числа, которые при сложении равны -11, а при умножении равны 31.
 Чтобы разложить x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как факторизовать любое квадратное уравнение в Precalculus I, MAT 161.
Чтобы разложить x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как факторизовать любое квадратное уравнение в Precalculus I, MAT 161.Резюме
В этом разделе представлены два метода факторинга. Первый — это общие факторы, в которых используется распределительное свойство ab + ac = a (b + c). Другой факторизирует трехчлены. Чтобы разложить трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, средний уровень алгебры, вы увидите больше факторов.
ГЛАВА 4 ОБЗОР
В этой главе вы познакомились с квадратиками. Двумя основными темами являются квадратичные формулы и графики квадратичных уравнений. Эти темы имеют множество приложений в бизнесе, физике и геометрии. Факторинг является важной темой в MAT 100, Intermediate Algebra.
Раздел 4.1: Введение в квадратные уравнения
Раздел 4.2: Применение квадратичных формул
Определение: ax 2 + bx + c = 0 — это квадратное уравнение.

Определение: квадратичная формула.
Пример 4. Фермер хочет обнести два соседних курятника против сарая. У него 125 футов забора. Какими должны быть размеры, если он хочет, чтобы общая площадь была 700 квадратных футов.
а. Заполните таблицу, чтобы найти уравнение площади.
б. Найдите W, если A = 700.
Размеры курятника площадью 700 квадратных футов составляют 35 на 20 футов и 6,667 на 105 футов.
(Чтобы получить длину, разделите 700 на 6,667 и 35)
Координата x вычисляется по формуле
Координата y вычисляется путем подстановки координаты x в y = ax 2 + бх + в. - Пересечение x:
Установите y = 0 и решите 0 = ax 2 + bx + c, используя квадратичную формулу. - Пересечение y:
Подставьте x = 0 в y = ax 2 + bx + c . Обратите внимание, что когда x = 0, y = c.
Пример 5. Уравнение затрат на изготовление коробок для сока: C = 0,6B 2 — 24B + 36, а уравнение дохода: R = -0,4B 2 + 18B . B в миллионах, а C и R в тысячах долларов.
B в миллионах, а C и R в тысячах долларов.
а. Найдите уравнение прибыли.
б. Нарисуйте график уравнения прибыли и объясните, что означают точки пересечения вершины, B и P с точки зрения задачи.
Вершина (21, 405).
Найдите перехват B. Установите P = 0,
Пересечения B равны (0,875, 0) и (41,13, 0).
Найдите точку пересечения P. Установите B = 0.
Пересечение P равно (0, -36).
г. Предположим, что компании необходимо получить 200 000 долларов прибыли (P = 200). Нарисуйте линию P = 200 и найдите, сколько коробок сока нужно произвести компании, чтобы заработать 200 000 долларов.
Компании необходимо произвести 6,682 или 35,32 миллиона коробок сока, чтобы заработать 200 000 долларов прибыли.
Вершина (21 405) представляет максимальную прибыль. Компания получит максимальную прибыль в размере 405 000 долларов, когда продаст 21 миллион коробок сока.





 5%)
5%)
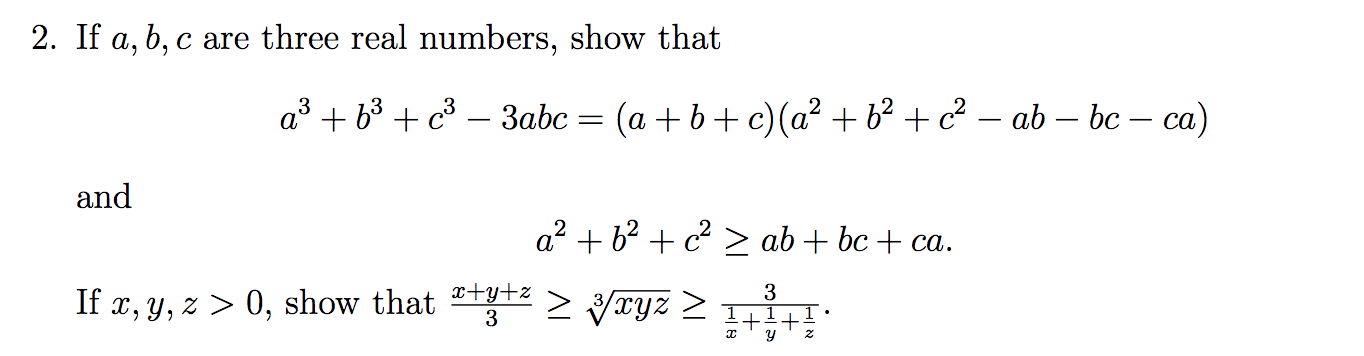
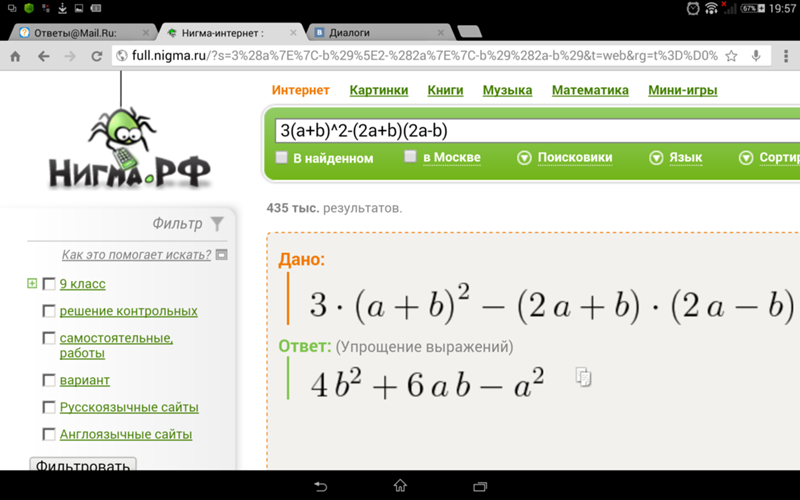
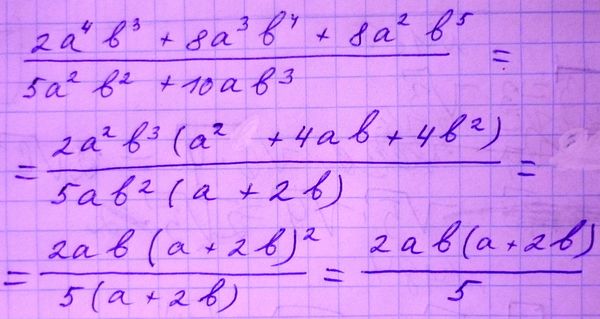


 ..
..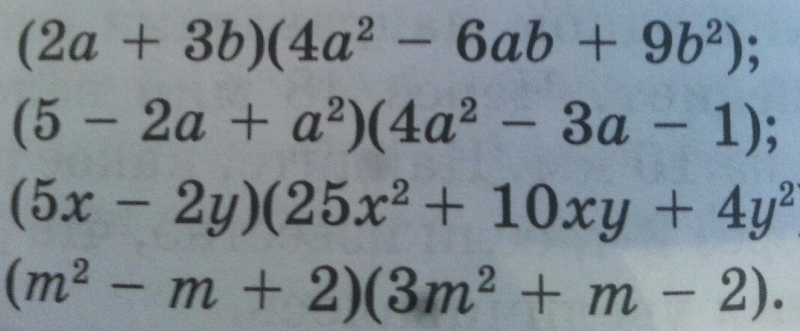 И что, следовательно, 2 равно 1. Вы бы подумали, что я сошел с ума? Больше похоже на полное безумие? Вероятно. Но орехи или нет, это именно то, о чем мы будем говорить сегодня.
И что, следовательно, 2 равно 1. Вы бы подумали, что я сошел с ума? Больше похоже на полное безумие? Вероятно. Но орехи или нет, это именно то, о чем мы будем говорить сегодня.
 Как же нам удалось доказать, что 2 = 1?
Как же нам удалось доказать, что 2 = 1? Но вы говорите, что это не деление на ноль — это деление на а — б . Это верно, но мы начали с предположения, что a равно b , а это значит, что a – b — это то же самое, что и ноль! И хотя вполне нормально делить обе части уравнения на одно и то же выражение, делать это неправильно, если выражение равно нулю. Потому что, как нас всегда учили, никогда нельзя делить на ноль!
Но вы говорите, что это не деление на ноль — это деление на а — б . Это верно, но мы начали с предположения, что a равно b , а это значит, что a – b — это то же самое, что и ноль! И хотя вполне нормально делить обе части уравнения на одно и то же выражение, делать это неправильно, если выражение равно нулю. Потому что, как нас всегда учили, никогда нельзя делить на ноль!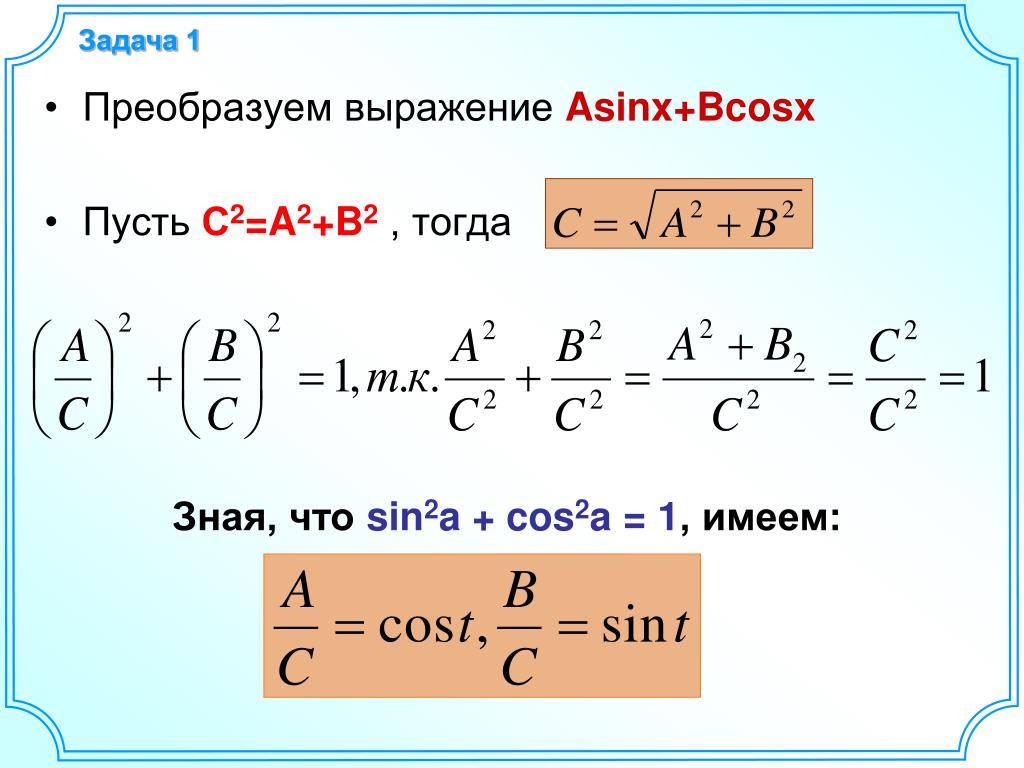 0758 х . Мы не знаем, что это такое, но просто предположим, что x — это какое-то число. Таким образом, 10/0 = x . Мы также можем рассматривать эту задачу деления как задачу умножения: какое число, x , нужно умножить на 0, чтобы получить 10? Конечно, на этот вопрос нет ответа, поскольку каждое число , умноженное на ноль, равно нулю. Это означает, что операция деления на ноль называется «неопределенной».
0758 х . Мы не знаем, что это такое, но просто предположим, что x — это какое-то число. Таким образом, 10/0 = x . Мы также можем рассматривать эту задачу деления как задачу умножения: какое число, x , нужно умножить на 0, чтобы получить 10? Конечно, на этот вопрос нет ответа, поскольку каждое число , умноженное на ноль, равно нулю. Это означает, что операция деления на ноль называется «неопределенной». В пределе, когда знаменатель этой дроби фактически становится нулем, результат был бы бесконечно большим.
В пределе, когда знаменатель этой дроби фактически становится нулем, результат был бы бесконечно большим.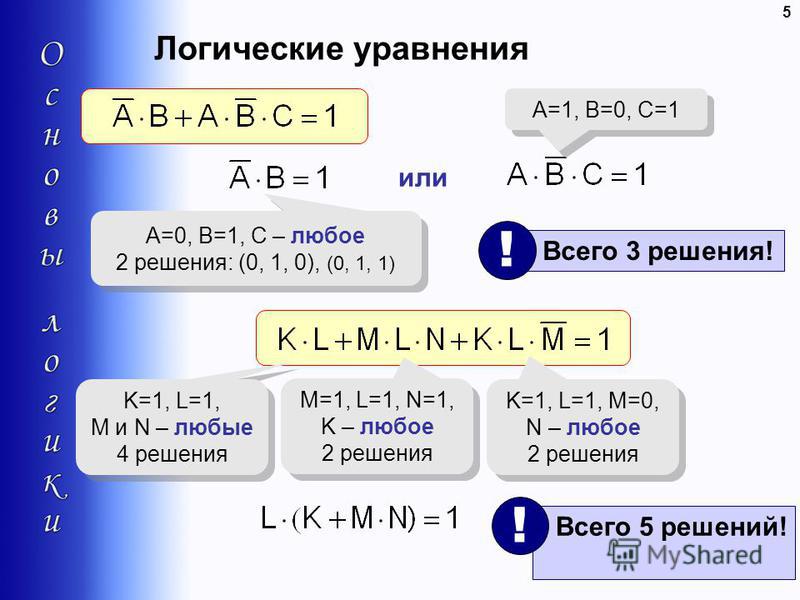
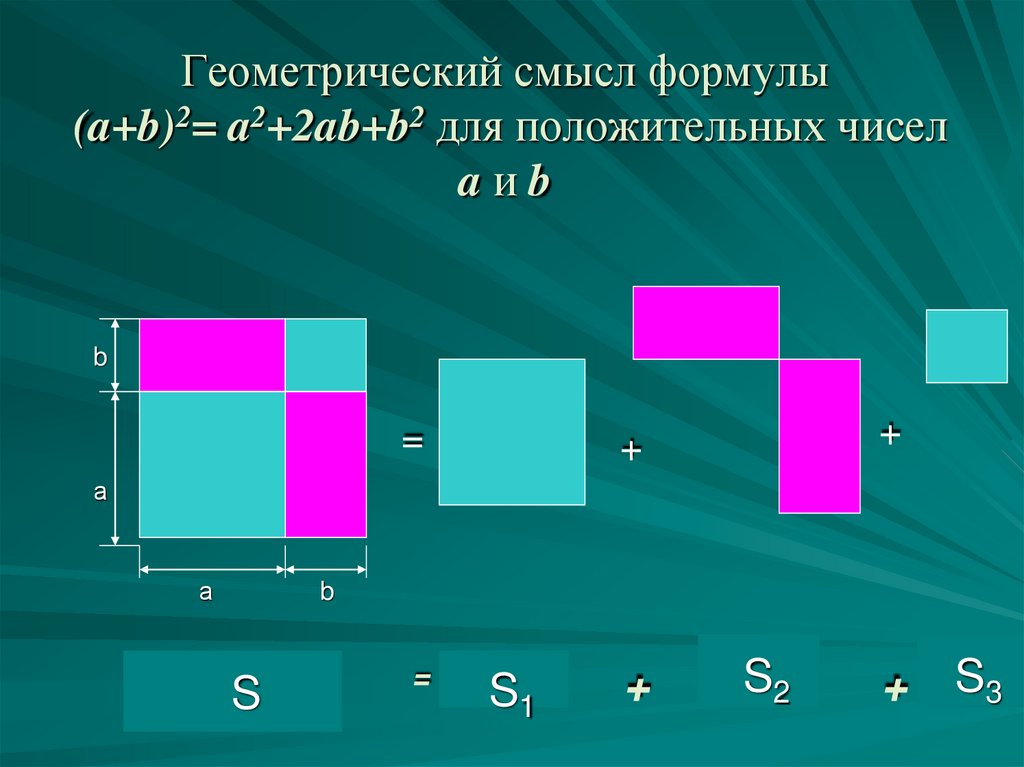 Квадратное уравнение, моделирующее высоту скалы, равно 9.0007
Квадратное уравнение, моделирующее высоту скалы, равно 9.0007
 Подобные термины , первоначально представленные в разделе 1.3 «Упрощение алгебраических выражений», имеют ту же переменную и тот же показатель степени. Например, 2x 2 и 5x 2 похожи, а 3x 2 и 7x — нет.
Подобные термины , первоначально представленные в разделе 1.3 «Упрощение алгебраических выражений», имеют ту же переменную и тот же показатель степени. Например, 2x 2 и 5x 2 похожи, а 3x 2 и 7x — нет.
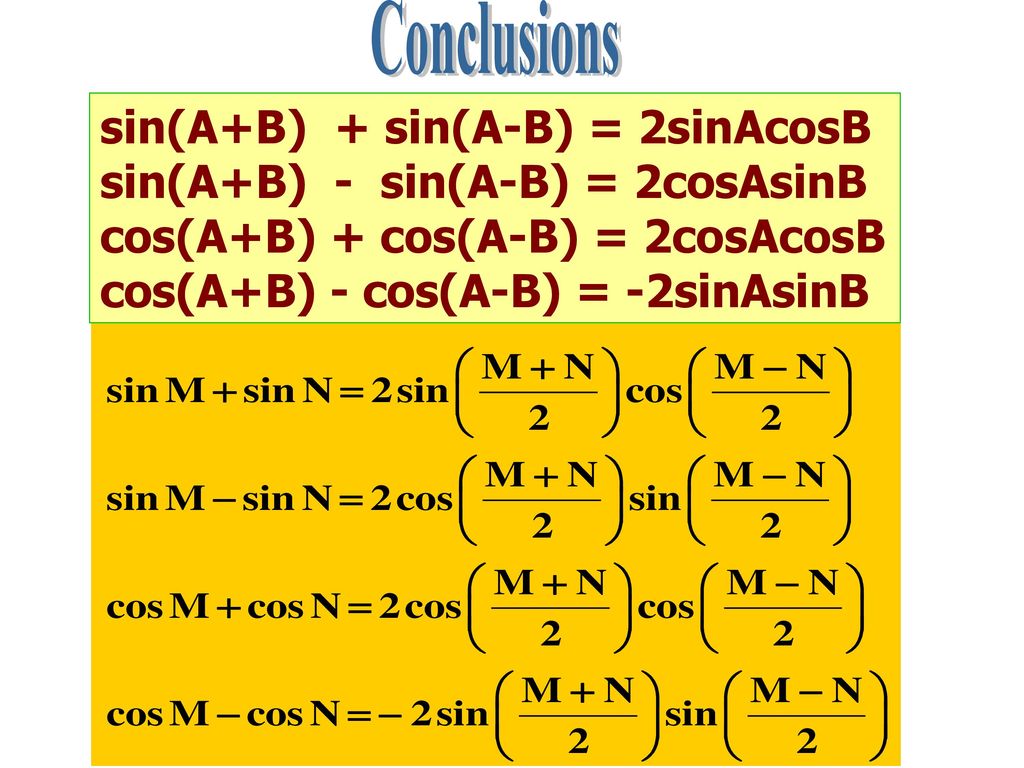

 Уравнение, которое моделирует высоту скалы над дном каньона:
Уравнение, которое моделирует высоту скалы над дном каньона:

 Эти точки будут интерпретироваться в приложениях.
Эти точки будут интерпретироваться в приложениях.

 (42, 1139).
(42, 1139). 
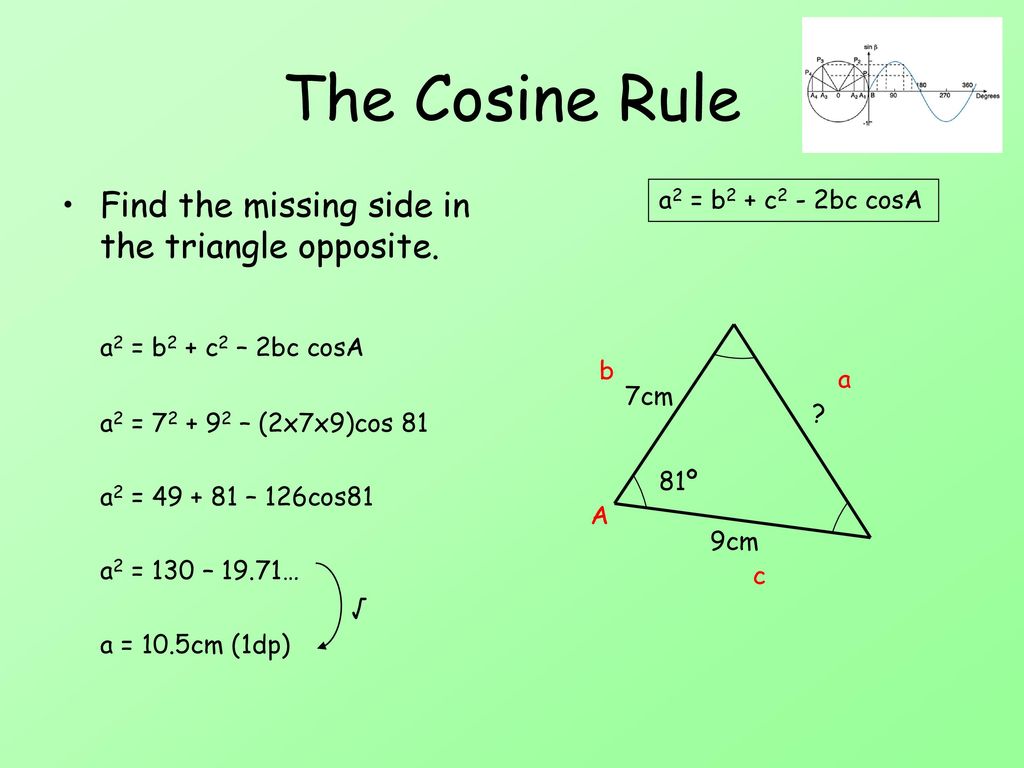 Если фермер использует 10 метров для ширины загонов, а их ширина 4, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений у него осталось по длине, из 9 вычтите 40.6, общее количество ограждений, доступных фермеру.
Если фермер использует 10 метров для ширины загонов, а их ширина 4, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений у него осталось по длине, из 9 вычтите 40.6, общее количество ограждений, доступных фермеру.


 В некоторых случаях они имеют U-образную форму, как в приведенном выше примере, или форму, как в примерах с 1 по 3. Если a в уравнении y = ax 2 + bx + c положительно, то график имеет U-образную форму, т. е. есть, открытие. Если a отрицательно, то график имеет форму, т. е. раскрывается вниз. Этот факт должен быть записан на карточке для заметок.
В некоторых случаях они имеют U-образную форму, как в приведенном выше примере, или форму, как в примерах с 1 по 3. Если a в уравнении y = ax 2 + bx + c положительно, то график имеет U-образную форму, т. е. есть, открытие. Если a отрицательно, то график имеет форму, т. е. раскрывается вниз. Этот факт должен быть записан на карточке для заметок. Обратите внимание, когда x = 0, y = c.
Обратите внимание, когда x = 0, y = c.
 Чтобы разложить трехчлены, вам нужно знать, как были вычислены 8x и 15. 8х получилось от сложения 5х и 3х, а 15 получилось от умножения 5 и 3.
Чтобы разложить трехчлены, вам нужно знать, как были вычислены 8x и 15. 8х получилось от сложения 5х и 3х, а 15 получилось от умножения 5 и 3.
 Чтобы разложить x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как факторизовать любое квадратное уравнение в Precalculus I, MAT 161.
Чтобы разложить x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как факторизовать любое квадратное уравнение в Precalculus I, MAT 161.